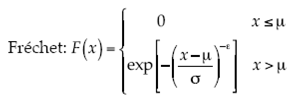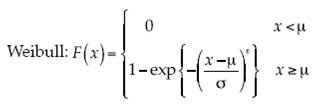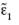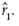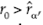Introducción
El agua es uno de los recursos naturales más valiosos de cualquier país debido a los beneficios sociales y económicos que se derivan de su consciente explotación; sin embargo, junto con las ventajas existen también situaciones extremas, como inundaciones y sequías (Zucarelli, 2013).
En el mundo, las inundaciones están aumentando más rápidamente que ningún otro desastre y han causado severos problemas tanto sociales como económicos. Por esta razón se han desarrollado diversas investigaciones para analizar eventos extremos y la forma de evaluar el riesgo de inundación. En México, Uribe-Alcántara, Montes-León y García-Celis (2010) propusieron un mapa de índices de inundación para identificar las zonas propensas a inundaciones.
El estudio de las inundaciones es complejo, pues, por ejemplo, el daño económico directo a un edificio inundado no sólo depende de la profundidad del agua sino también del uso del inmueble. Otros factores importantes son las características del edificio, las variables socioeconómicas y la calidad de la respuesta de emergencia, entre otras (Smith, 2001). En la Ciudad de México, Baró-Suárez, Díaz-Delgado, Calderón-Aragón, Esteller-Alberich y Cadena Vargas (2011) realizaron una investigación sobre el costo más probable de daños en zonas habitacionales y propusieron una caracterización de costo con base en el índice de marginación urbana.
Existen diferentes formas de examinar las inundaciones. Hunt las analiza como un desastre natural en el que se deben identificar los peligros y la vulnerabilidad para poder superarlos (Hunt, 2002). El Centro Nacional de Prevención al Desastre (Cenapred, 2006), por el contrario, no maneja los desastres como naturales sino como producto de las condiciones de vulnerabilidad y exposición. Entonces, si lo que se desea es prevenir los desastres, es necesario hablar de riesgo. Es posible señalar varias definiciones de riesgo, que se basan principalmente en los factores de los que depende su estimación. Además es importante mencionar que los efectos de las inundaciones en la sociedad no pueden ser representados en una cotización monetaria (Green, Van Der Veen, Wiertra, & Penning-Rowsell, 1994).
En algunos otros trabajos, Herrera-Díaz, Rodríguez-Cuevas, Couder-Castañeda y Gasca-Tirado (2015), así como Flowers-Cano, Jeffrey-Flowers y Rivera-Trejo (2014), al igual que Young (2002), combinan los métodos estadísticos y determinísticos para analizar datos pasados y predecir los niveles de inundación y de ríos. Por su parte, Bayliss y Reed (2001) discuten diferentes formas de estudiar las inundaciones históricas y revisan métodos para incorporar datos históricos al análisis de frecuencias de inundaciones. Se puede incorporar información meteorológica para fortalecer la estimación del riesgo; la lluvia puede ser un notorio indicador fiable de la inundación (Duncan, 2002). Sin embargo el riesgo abarca dos aspectos: peligro (P) y vulnerabilidad (V) (Mileti, 1999), aunque si bien no es la única definición que se maneja para el riesgo, sí es una de las más utilizadas. Ordaz incluye un tercer factor para la expresión del cálculo de riesgo por algún fenómeno natural (Ordaz, 1996), el costo (C) o valor de los bienes expuestos; entonces, el riesgo es producto de tres factores: R = V × C × P. Nótese que en realidad se trata de la misma definición, ya que la vulnerabilidad está compuesta de dos elementos: exposición o daño potencial, y susceptibilidad o pérdida (Merz, Thieken, & Gocht, 2007). Por lo tanto, para obtener una medida del riesgo, se debe trabajar sobre estos tres últimos factores.
Debido al impacto de las inundaciones sobre la sociedad y las pérdidas monetarias, es importante la construcción de un índice de vulnerabilidad (Tapsell, Penning-Rowsell, & Tunstall, 2002). La vulnerabilidad tiene diferentes conceptos, por ejemplo, Blaikie, Wisner, Cannon y Davis (1994) analizan las condiciones socioeconómicas que aumentan el grado de vulnerabilidad.
En cuanto al peligro, se deben calcular las probabilidades de que ocurra un fenómeno que pueda dañar lo expuesto (Ordaz, 1996). Por el efecto de las inundaciones, el riesgo puede ser generado por lluvias, ciclones tropicales o falla de obras hidráulicas.
En este artículo, las inundaciones se estudian cuando se registran valores extremos de precipitaciones de lluvias y es aquí donde se introducirá la teoría sobre valores extremos.
Fisher y Tippett (1928) derivaron la forma límite de la distribución del valor máximo de una muestra aleatoria, encontrando las tres posibles distribuciones: Gumbel, Weibull y Fréchet. A partir de esto se desarrollan aportaciones de interés como las de Gumbel (Gumbel, Les moments des distribution limite du terme maximum dùne sèrie alèatoire, 1934), quien además presenta el primer libro de importancia (Gumbel, Statistical of Extremes, 1958), en el que trabajó con eventos extremos contemplando varias aplicaciones. Por su parte, Gnedenko presenta en forma general y con una prueba rigurosa el teorema de los tipos de distribución para valores extremos propuesto por Fisher y Tippett (Gnedenko, 1943). Otra aportación importante la dieron Von Mises (1936) y Jenkinson (1955), quienes trabajaron sobre la distribución de valores extremos y propusieron una distribución que combina las tres familias de distribución de valores extremos, la cual es conocida como DVEG. De 1990 a 2011, el desarrollo estadístico ha sido sustancial en el área, como en el caso, entre otros, de Tawn (1992), Rosbjerg y Madsen (1996), Coles y Dixon (1999, Likelihood-Based Inference for Extreme Values Models Extremes) y Coles (2001, An Introduction to Statistical Modeling of Extreme Values).
Obtenida una medida del riesgo, se implementan los mapas de peligro y riesgo por inundación para ubicar las zonas en diferentes categorías de riesgo y desarrollar un plan de manejo. Tawatchi y Mohammed (2005), y Lehner y Döll (2001) proporcionan un ejemplo para aproximar a escala global el análisis con mapas concernientes a la situación de inundación en Europa; en cuanto a México, se tienen los mapas de riesgo a escala municipal por inundaciones (Cenapred, 2006).
En México, en la región del sistema Grijalva- Usumacinta del estado de Tabasco se han presentado inundaciones en los últimos años. Una de ellas, en 2007, fue una de las de mayor intensidad en los últimos 50 años (Rivera-Trejo, Soto-Cortés, & Barajas-Fernández, 2009). Por su parte, Arreguín-Cortés, Rubio-Gutiérrez, Domínguez- Mora y Luna-Cruz (2014) analizaron los factores que influyen en las inundaciones de la planicie tabasqueña, como la ausencia de ordenamiento territorial adecuado y la deforestación de la parte alta de las cuencas.
Por esta razón, en la presente investigación se calculan los índices para el riesgo de inundación y sus periodos de retorno con cuatro escenarios de peligro: 100, 150, 200 y 250 mm. Para esto se propone una prueba de bondad de ajuste bootstrap paramétrica basada en el coeficiente de correlación muestral, y se comprueba el tamaño y potencia de la prueba por simulación realizando 10 000 réplicas.
Objetivo general
Modelar el riesgo de inundaciones en el estado de Tabasco por causas climáticas extremas.
Objetivos específicos
Proponer un modelo estadístico basado en la teoría de valores extremos que permita determinar el comportamiento y las tendencias de las precipitaciones extremas.
Calibrar el modelo estadístico usando una base de datos histórica de precipitación y niveles hidrométricos del estado de Tabasco.
Construir un mapa de riesgo de inundaciones por municipio en el estado de Tabasco.
Metodología
Por lo común se cree que el peligro es el único responsable de los desastres, pero en buena medida es la sociedad la que se expone con su infraestructura, organización y cultura para enfrentar fenómenos con alto grado de peligro. Por lo tanto, se debe entender que los desastres no sólo son naturales, sino que también son producto de condiciones de vulnerabilidad y exposición (Cenapred, 2006).
Por lo anterior, es necesario encontrar una medida que represente el riesgo y sus cambios a través del tiempo; puede ser estadísticamente difícil de modelar debido a la gran cantidad de variables que intervienen en el modelo. Una forma de tratar y aligerar la solución a este problema puede ser introduciendo los números índice. Los índices, desde su aparición, han llegado a ser cada vez más importantes como indicadores de los diferentes cambios que rodean a la sociedad.
En este trabajo se van a construir los índices y mapas de riesgo a escala municipal en el estado de Tabasco. Para el riesgo se utilizará la definición de Ordaz (1996), quien maneja al riesgo como el producto de tres factores (ver expresión (1)). Para cada uno de éstos se calculará un indicador:
En donde V representa la vulnerabilidad, C, el valor de los bienes expuestos y P es el peligro o probabilidad de ocurrencia de un fenómeno que pueda dañar lo expuesto.
Vulnerabilidad
La vulnerabilidad puede tener diferentes conceptos. En este artículo se considera como una medida de qué tan susceptible es un bien expuesto a la ocurrencia de un fenómeno perturbador (Ordaz, 1996). Para su análisis se consideran dos variables: por un lado, los servicios con los que cuenta la comunidad (energía eléctrica, agua potable y drenaje) y, por el otro, sus principales recursos hidrológicos (ríos y lagunas).
En el caso de los servicios, se construye un índice de servicios a través de tres variables:
PO_NDEE: porcentaje de ocupantes que no dispone de energía eléctrica.
PO_NDAE: porcentaje de ocupantes que no dispone de agua entubada.
PO_NDD: porcentaje de ocupantes que no dispone de drenaje.
Estos factores son ponderados mediante el uso de componentes principales (CP) del análisis multivariado. El uso de CP garantiza una combinación lineal con máxima varianza que brinda los mejores coeficientes y que explica de modo adecuado la situación de la comunidad.
La segunda variable, recursos hidrológicos con los que cuenta cada municipio, es considerada debido a que la región de Tabasco está a muy poca altura sobre el nivel del mar; es una zona de ríos, lagunas y pantanos. Además, a lo largo de su historia, Tabasco ha sufrido inundaciones por el desbordamiento de los ríos que atraviesan la entidad. Por ejemplo, la inundación de 2007 (Rivera-Trejo et al., 2009) en el municipio de Paraíso se debió al exceso de lluvia que coincidió con el oleaje en el Golfo de México, que evitó las descargas de los ríos Grijalva y Carrizal hacia el mar. Entonces, para los recursos hidrológicos, se construye un índice de ríos a través de una ponderación por municipio que depende del número de ríos que se encuentren en él, además de considerar la capacidad de cada uno de los ríos según la información del nivel de agua máximo ordinario (NAMO).
Costo de los bienes expuestos
La componente costo, C, de la ecuación (1) mide la cuantía de lo que es susceptible de afectarse durante la ocurrencia de un fenómeno perturbador (Ordaz, 1996). Entonces, para la construcción de un indicador de costo, se consideran los bienes con los que cuenta la población (televisión, lavadora, refrigerador, computadora, automóvil) y el número de habitantes por comunidad. El número de habitantes se toma en cuenta por el supuesto de que "A mayor población, mayor riqueza". Entonces, el índice de costo de bienes expuestos se construye con base en los siguientes cinco indicadores de bienes, que después serán ponderados mediante el uso de componentes principales:
PODT: porcentaje de ocupantes que dispone de televisión.
PODR: porcentaje de ocupantes que dispone de refrigerador.
PODL: porcentaje de ocupantes que dispone de lavadora.
PODC: porcentaje de ocupantes que dispone de computadora.
PODA: porcentaje de ocupantes que dispone de automóvil o camioneta.
Peligro
El peligro, P, de inundación en el contexto de esta investigación se define como la probabilidad de ocurrencia de una situación de inundación potencialmente dañina en un área dada y con cierto periodo especificado. Para el análisis de este componente, la información a utilizar dependerá del tipo de inundación que se analice y pueden definirse de acuerdo con:
La duración de la inundación: lenta o súbita.
El mecanismo que las genere: pluviales, fluviales, costeras o falla de obras hidráulicas.
En este caso, se calcula un valor para el peligro tomando a la lluvia como un indicador fiable de la inundación; no se estudian las inundaciones dadas directamente por fallas de obras hidráulicas, aunque es importante hacer notar que cuando se presentan valores extremos de precipitación es muy probable que ocurran fallas en obras hidráulicas. Por tanto, para el cálculo del factor peligro se analizan los datos de precipitación en Tabasco y zonas cercanas; estas últimas se consideran, pues las inundaciones no dependen sólo de la precipitación local, sino de la precipitación en la cuenca aguas arriba del punto de desborde.
Datos de precipitación
La información de la precipitación se obtuvo de las mediciones diarias -desde 1961 hasta 2007- de precipitación tomadas en las estaciones registradas por el Servicio Meteorológico Nacional (SMN) con la herramienta CLICOM, en su versión interpolada en malla regular de 0.2 grados de longitud por 0.2 grados de latitud (Maya v. 1.0).
Para obtener la base de datos de cada municipio se delimitó una región para cada uno. Esto se realizó con ayuda de la información de las subcuencas, cuyo caudal influye en el municipio de estudio (ya sea parcial o totalmente). En caso de que parte de alguna subcuenca entre en el municipio, pero la aportación de su caudal no influya, se toman sólo los nodos que se encuentren dentro del municipio. Con esto se determina cuáles son los nodos que influyen en el análisis, así se tendrán tantas series de datos como el número de nodos incorporados en el estudio. Entonces, para obtener una sola serie, se realiza una combinación lineal, que resulte adecuada, de los nodos considerados. Para esto nuevamente se utiliza la teoría de componentes principales; en este caso, las variables son los nodos del municipio. Las CP obtenidas corresponden a los pesos dados a cada nodo para obtener la combinación lineal deseada que finalmente será la serie de datos que represente al municipio.
Análisis de los datos
Dadas las series de datos de cada municipio, se extraen las precipitaciones máximas anuales. Sea x 1, x 2,... x m una muestra de la variable aleatoria X i: precipitación en el municipio i. Entonces se forman los vectores x (1) = (x 1 1, ..., x 1 n), x (2) = (x 2 1, ..., x 2 n), x ( k ) = ( x k 1, ..., x k n). Con los vectores se calculan los máximos anuales, M n,i = máx{x i 1 , ..., x i n }, i = 1, ..., k, que gracias a la teoría de valores extremos se consideran iid (independientes e idénticamente distribuidos), entonces F(x) = P(M ≤ x) = {F(x)} k. Por el teorema de Fisher y Tippett (1928) se asume que Mn,i sigue una de las distribuciones de valores extremos (DVE) mostradas en (2), (3) y (4):
con parámetros  o bien con su generalización dada por Gnedenko, la distribución de valores extremos generalizada (DVEG), mostrada en (5):
o bien con su generalización dada por Gnedenko, la distribución de valores extremos generalizada (DVEG), mostrada en (5):
donde y+ = 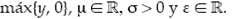 En esta investigación se estudió el ajuste con la distribución Gumbel, por ser una de las más empleadas en el campo de las inundaciones en México, y la DVEG, cuyo uso se ha ampliado en los últimos años, pero aún no es muy aplicada para las precipitaciones máximas en México. Los parámetros μ, σ y ε se estiman por el método de máxima verosimilitud, para aprovechar las propiedades asintóticas de estos estimadores y obtener los intervalos de confianza de forma sencilla. La función log-verosimilitud para la DVEG y la distribución Gumbel están dadas en (6):
En esta investigación se estudió el ajuste con la distribución Gumbel, por ser una de las más empleadas en el campo de las inundaciones en México, y la DVEG, cuyo uso se ha ampliado en los últimos años, pero aún no es muy aplicada para las precipitaciones máximas en México. Los parámetros μ, σ y ε se estiman por el método de máxima verosimilitud, para aprovechar las propiedades asintóticas de estos estimadores y obtener los intervalos de confianza de forma sencilla. La función log-verosimilitud para la DVEG y la distribución Gumbel están dadas en (6):
Sean  los estimadores de máxima verosimilitud (EMV) de
los estimadores de máxima verosimilitud (EMV) de  , éstos se calculan con las librerías evd y VGAM del Proyecto R. Para la estimación por intervalos, se usa el hecho de que los EMV se distribuyen asintóticamente normal
, éstos se calculan con las librerías evd y VGAM del Proyecto R. Para la estimación por intervalos, se usa el hecho de que los EMV se distribuyen asintóticamente normal  , donde
, donde  es la matriz de información de Fisher. Entonces, el intervalo de confianza a (1 - α)100% para cada componente de q está dado por
es la matriz de información de Fisher. Entonces, el intervalo de confianza a (1 - α)100% para cada componente de q está dado por  , en donde Zα/2 es el valor de la variable normal estándar con área derecha igual a α/2, y cii es el i-ésimo elemento de la diagonal
, en donde Zα/2 es el valor de la variable normal estándar con área derecha igual a α/2, y cii es el i-ésimo elemento de la diagonal  .
.
Elección del modelo
La elección del modelo se basó principalmente en el criterio de información de Akaike (AIC), AIC(k) = -2log(L(θk)) + 2k, donde k es el número de parámetros del modelo y log(L(θk)) es el logaritmo de la verosimilitud del modelo, considerando mejor modelo si tiene menor valor de AIC. Un segundo criterio para modelos con la misma cantidad de parámetros es el valor del logaritmo de la verosimilitud (log-veros), eligiendo el modelo que tenga mayor valor de log-verosimilitud. El tercer criterio asume que existe una relación lineal entre la distribución empírica y la distribución teórica correspondiente, Gumbel (2) o VEG (5), por lo que se emplea el coeficiente de correlación muestral (7) como medida de asociación y se prefiere el modelo cuyo coeficiente de correlación muestral sea más cercano a uno:
Prueba bootstrap basada en el coeficiente de correlación muestral
Sea X1,..., Xn una muestra aleatoria de una función de distribución FX(x) = P (X ≤ x). El contraste de hipótesis a probar está dado por:
donde F*(x) denota una familia de densidades específica; en este caso se trata de la función de densidad Gumbel y la DVEG.
Las densidades que se analizan en esta investigación son del tipo localidad y escala (Gutiérrez-González, Panteleeva, & Córdoba- Lobo, 2012) cuando se fija un valor para el parámetro de forma. Así, con base en la invarianza bajo la transformación de los parámetros de localidad y escala, se propone una prueba de bondad de ajuste bootstrap paramétrico basada en el coeficiente de correlación muestral, como una estadística de prueba. Una prueba similar a ésta para la distribución log-gamma generalizada fue presentada por Gutiérrez-González, Villaseñor-Alva, Panteleeva y Vaquera-Huerta (2013).
Si H 0 de (8) se cumple, entonces la distribución de f(x) es tal que  Entonces, para una variable aleatoria X con función de densidad f(x), se tiene que la función F*(x;ε) le corresponde su función inversa
F-1
* (y;ε) en y.
Entonces, para una variable aleatoria X con función de densidad f(x), se tiene que la función F*(x;ε) le corresponde su función inversa
F-1
* (y;ε) en y.
Sean X(1),..., X(n) las estadísticas de orden de una variable aleatoria, entonces la función de distribución empírica correspondiente está dada por:
donde x (i) es el valor de la i-ésima estadística de orden.
Por el teorema de Glivenko-Cantelli se establece una convergencia casi segura, cuando n → ∞, entre la distribución empírica Fn(x) y la distribución teórica, que puede ser F(x) o G(x); por lo tanto, es factible establecer para la DVEG una aproximación:
Similarmente, para la distribución Gumbel resulta:
Ambas expresiones se pueden reescribir como Y = β + αZ y se espera que bajo H 0 exista una fuerte relación lineal entre Y y Z cuando se sustituye al parámetro ε por un estimador consistente 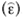 . Entonces, para probar el contraste de hipótesis de (8), se propone como estadística de prueba al coeficiente de correlación muestral dado en (7), en el cual se espera que bajo H 0 la distribución de rn(Y,Z) estará concentrada en las proximidades de 1. Por tanto, la regla de decisión para una prueba de tamaño a, con a ∈ (0,1), un valor conocido, consiste en rechazar H 0 cuando
. Entonces, para probar el contraste de hipótesis de (8), se propone como estadística de prueba al coeficiente de correlación muestral dado en (7), en el cual se espera que bajo H 0 la distribución de rn(Y,Z) estará concentrada en las proximidades de 1. Por tanto, la regla de decisión para una prueba de tamaño a, con a ∈ (0,1), un valor conocido, consiste en rechazar H 0 cuando 
La prueba bootstrap con base en los EMV se realiza siguiendo los siguientes pasos:
1. Dadas las observaciones x1,... xn, calcular un valor para el estimador de ε, denotado por 
2. Con las observaciones se calcula su coeficiente de correlación muestral r0 .
3. A partir de  iniciar un ciclo bootstrap.
iniciar un ciclo bootstrap.
4. El ciclo de bootstrap del inciso 3 se repite m veces para calcular,  , en donde m cantidad de estimaciones de bootstrap, para determinar el cuantil bootstrap.
, en donde m cantidad de estimaciones de bootstrap, para determinar el cuantil bootstrap.
5. Con el ciclo terminado,  son ordenados en forma no decreciente, denotándolos con
son ordenados en forma no decreciente, denotándolos con  . Entonces,
. Entonces,  y obtener el cuantil α, sea éste
y obtener el cuantil α, sea éste 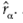
6. Regla de decisión. Comparar r0 con el cuantil α del paso 5.
Antes de iniciar con las pruebas, se determina si éstas conservan el tamaño nominal de la prueba y presentan buenas potencias.
Los resultados de los tamaños de la prueba para 10 000 réplicas de ambas distribuciones se muestran en el cuadro 1. Se puede concluir que la prueba bootstrap conserva el tamaño nominal de la prueba para las distribuciones Gumbel y VEG.
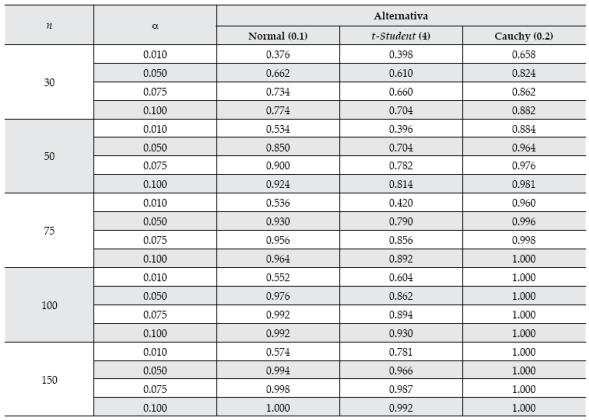
En el caso de la potencia de la prueba se utilizan tres diferentes distribuciones alternativas: normal estándar, t-Student con 4 gl y Cauchy (0.2). Los resultados para 10 000 réplicas se muestran en el cuadro 2.
Periodos de retorno
Para el análisis del factor peligro es de interés conocer el tiempo promedio de espera para que ocurra una lluvia extrema que pudiera causar algún problema de inundación. El periodo de retorno es el tiempo medio para que se repita un evento semejante. Entonces sea X1, X2
, ... una sucesión de variables aleatorias iid con función de distribución continua F y μ ∈  . Considerando {Xi > u} un evento extremo, se define el tiempo de la primera excedencia como T(u) = mín{i ≥ 1:Xi > u}. Con esto, el tiempo promedio de espera para que ocurra un evento extremo es E[T(u). Si la probabilidad del evento {X * i > u} es p, su periodo de retorno es p-1. Entonces, usando la distribución de probabilidad acumulada, para el evento {Xi > u}, el periodo de retorno se calcula con (9):
. Considerando {Xi > u} un evento extremo, se define el tiempo de la primera excedencia como T(u) = mín{i ≥ 1:Xi > u}. Con esto, el tiempo promedio de espera para que ocurra un evento extremo es E[T(u). Si la probabilidad del evento {X * i > u} es p, su periodo de retorno es p-1. Entonces, usando la distribución de probabilidad acumulada, para el evento {Xi > u}, el periodo de retorno se calcula con (9):
En específico, el nivel de retorno asociado con el periodo de retorno p-1 es el (1 - p)-ésimo cuantil de la distribución. En el caso de la distribución Gumbel y la de VEG, el cuantil 1 - p está dado en (10):
Los cuantiles se calculan a partir de las estimaciones de los parámetros.
Resultados y discusión
El índice de riesgo se calcula con la fórmula (1). Para los factores de vulnerabilidad y de costo se construyen dos indicadores con base en la disposición de servicios, de los bienes con los que cuenta la población y del número de habitantes por municipio. La información fue tomada de la base de datos de INEGI, que corresponde al censo de población y vivienda 2010.
Índice de vulnerabilidad
La vulnerabilidad se compone de dos factores: social y natural. El factor social se refiere al indicador de servicios (Ind serv) que se obtiene a partir de una combinación lineal de las tres variables PO_NDEE, PO_NDAE y PO_NDD. Los pesos de la combinación lineal se obtienen por CP. Con la información de las tres variables se calcula la matriz de covarianzas y de ésta, los valores propios de cada una de las variables, resultando 290.367, 6.808 y 1.228, respectivamente. Después se ponderan los valores propios. Resultan los pesos de cada una de las tres variables. Para obtener el Indserv , los resultados se muestran en el cuadro 3.
Para el factor natural se propone el indicador ríos (Inríos ), en donde se consideran los principales recursos hidrológicos con los que cuenta cada municipio. El indicador se construye ponderando el número de ríos que forman parte del municipio y la capacidad que tiene cada uno, medida por el nivel de agua máximo ordinario. Los resultados del Inríos se muestran en el cuadro 3.
Por último, para obtener el indicador de vulnerabilidad (Invuln ), se ponderaron ambos indicadores, Inserv e Inríos . Los resultados se muestran en el cuadro 3.
Índice de costos
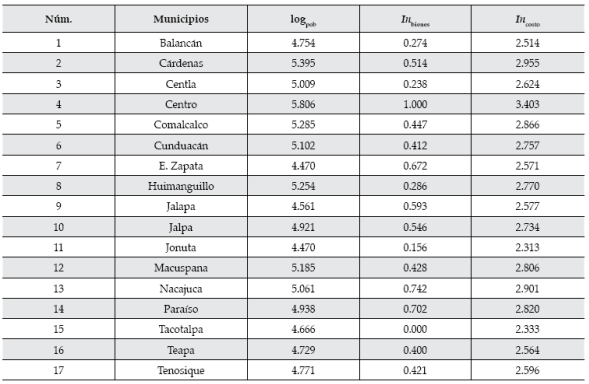
Para el análisis del factor de costo intervienen dos variables de interés. En primer lugar, se tiene el logaritmo del número de habitantes en cada municipio, esto basado principalmente en el supuesto de que a mayor población mayor riqueza. Se toma el logaritmo de la población (logpob) sólo para mantener una escala más apropiada. Los resultados se muestran en el cuadro 4.
La segunda variable que se toma en cuenta es un indicador de los bienes (Inbienes) con los que cuenta la población del municipio en estudio. Después, en la construcción de este indicador se consideraron cinco bienes que estarían expuestos a sufrir cierto daño ante una inundación y se denotan de la siguiente manera: televisión (PODT), refrigerador (PODR), lavadora (PODL), computadora (PODC), y automóvil o camioneta (PODA). En el cálculo del indicador de bienes se consideraron los porcentajes de la población que cuenta con tal o cual bien.
Para obtener una combinación lineal adecuada de estas cinco variables se realiza un análisis de CP para generar los pesos adecuados de cada variable. De forma similar al caso de los servicios, se calcula la matriz de covarianzas y se calculan los valores propios para las cinco variables mencionadas arriba, obteniendo 243.062, 17.619, 5.178, 3.471 y 1.405, respectivamente. Realizando una ponderación a partir de los valores propios, resultan los pesos de cada una de las cinco variables. Los resultados se muestran en el cuadro 4.
Por último, para obtener el indicador de costo (Incosto), se hace una ponderación de los factores logpob y Inbienes que influyen en este indicador. Cabe mencionar que no existe alguna razón relevante para darle mayor peso a un factor en particular, entonces se restringe a ponderar con el mismo peso a ambos factores, es decir, 0.5 para los dos. Los resultados se muestran en el cuadro 4.
Factor peligro
Obtención de la información
Para calcular los índices de peligro, la información de precipitación se obtuvo de las mediciones proporcionadas en la base de datos que el Servicio Meteorológico Nacional maneja con la herramienta CLICOM, desde 1961 hasta 2000, en su versión interpolada en malla regular de 0.2 grados de longitud por 0.2 grados de latitud (la denominada Maya v. 1.0). La información proviene de algo más de 5 000 estaciones climatológicas de la base de datos. La información más reciente (2001-2007) proviene de las mediciones diarias del subconjunto de estaciones climatológicas que reporta en tiempo casi real; estos datos fueron obtenidos con base en su longitud y latitud.
Los datos utilizados son los de precipitación pluvial y en la presentación de nodo por nodo. Lo que se tiene es una lista de 4 542 archivos de texto en donde cada uno de éstos corresponde a un nodo y cada archivo contiene una serie de datos de precipitación pluvial desde enero de 1961 hasta diciembre de 2000. Además de esta información, se conoce la precipitación de 2001 a 2007 de las estaciones existentes en la república mexicana. Se cuenta con un archivo por año con cada uno con los siguientes campos: latitud, longitud, clave y nombre de la estación, altura, mes y días. Para aprovechar la información extra se trabajó con las estaciones que rodean al nodo. Con cada nodo que se encuentra involucrado en el análisis se calcula un valor máximo de precipitación de 2001 a 2007 y se obtiene la precipitación que corresponde al nodo de interés.
Los nodos de interés son los que intervienen en cada municipio. Para esto se localizan las cuencas que conforman al estado de Tabasco. La mayor parte de la superficie del estado (75.22%) se ubica en la Región Hidrográfica número 30, o Región del Sistema Grijalva-Usumacinta, formada por las cuencas hidrográficas del Grijalva, Usumacinta y de la laguna de Términos, que en Tabasco ocupan el 41.45, 29.24 y 4.53%, respectivamente.Mientras que el 24.78% restante se encuentra dentro de la Región Hidrográfica número 29 o Región del Coatzacoalcos, formada por dos cuencas: la del Coatzacoalcos, Tonalá y lagunas del Carmen, y la Machona, siendo esta última la única que tiene representación en el estado. Ambas regiones están consideradas como las más húmedas del país, en primer y segundo lugar, respectivamente.
Con base en la información que se conoce de vulnerabilidad y costo se trabaja por municipio. Entonces, para obtener los datos de precipitación en cada municipio se utilizó la información de las subcuencas que forman parte de cada uno de éstos, ya sea que se encuentre completamente solo o como parte de ella, y se toman en cuenta aquellas cuya aportación de su caudal influye en el municipio de estudio.
Análisis de la información
En el análisis de los datos se requiere de una serie de observaciones para cada municipio, pero en este caso se tienen tantas series como el número de nodos que se involucren. Entonces, para obtener una sola serie se realiza una combinación lineal que resulte adecuada de los nodos que entran en el municipio. Para tener la mejor combinación lineal, se utiliza CP con los nodos de cada municipio, esto proporcionará la serie final de los datos de precipitación del municipio de interés.
Para el factor peligro, a los datos de precipitación se les extrajeron los máximos anuales a los que se ajustaron la distribución Gumbel y de VEG; en ambas se realizó una estimación puntual y por intervalos. Se consideraron los tres criterios mencionados en la sección anterior y se eligió el modelo en el que dos o más criterios le favorecieran para modelar el municipio de interés.
En los cuadros 5 y 6 se muestran los resultados de las estimaciones y en la figura 1, las gráficas correspondientes al municipio de Balancán, Tabasco. La misma estimación se realizó para los 16 municipios restantes. En el cuadro 7 se ejemplifican con cuatro municipios los modelos elegidos.
Una vez obtenidos los modelos para los 17 municipios, se calculan sus respectivos periodos de retorno. En el cuadro 8 se muestran los resultados bajo cuatro escenarios de peligro: 100, 150, 200 y 250 mm. Por ejemplo, para Balancán se tiene que el tiempo promedio para que ocurra una lluvia mayor o igual a 150 mm es de 3.5 años.
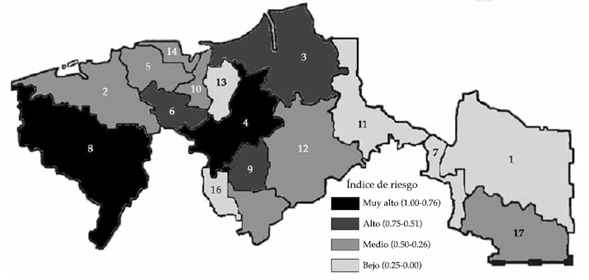
Finalmente, con los resultados de los tres factores se construye el Índice de Riesgo de Inundación; en el peligro se toma la probabilidad p del evento {Xi > x}, donde x = 150 mm, ya que la experiencia sugiere que a partir de este valor se han presentado problemas de inundación. Los resultados se muestran en el cuadro 9 y en la figura 2 se tiene el mapa de riesgo de inundación.
Discusión de resultados
La prueba de bondad de ajuste boostrap propuesta conserva los valores nominales del tamaño de la prueba y las potencias bastante altas, lo que la hace una mejor prueba para las DVEG que la presentada por Campos-Aranda (2001). En investigaciones previas sobre lluvias se tienen trabajos que abarcan sólo los valores históricos (González-Camacho, Pérez-Rodríguez, & Ruelle, 2011), (Coronel-Brizio & Llanos-Arias, 1996; Díaz-Delgado, Bâ, & Trujillo-Flores, 1999); similarmente, para la vulnerabilidad existen trabajos que se relacionan con este factor (Green et al., 1994) y lo mismo para el de costos en zonas habitacionales (Baró-Suárez, Díaz-Delgado, Calderón-Aragón, Esteller-Alberich, & Cadena- Vargas, 2011). En la investigación hecha para el riesgo de inundaciones, el índice propuesto está basado en el ACP e incluye todas las variables sobre las que se tiene información, agrupadas en los tres factores mencionados (Ordaz, 1996), proporcionando de esta forma una medida más confiable para monitorear el riesgo por inundación en los 17 municipios del estado de Tabasco.
Conclusiones
El mapa de riesgo obtenido fue contrastado con los resultados históricos sobre desastres por inundación en los 17 municipios de Tabasco. Los resultados obtenidos fueron acordes con los registros de inundaciones en los años 1982, 1989, 1995, 1998, 2002, 2003, y de 2005 a 2009. En el cuadro 10 se muestra el comparativo del índice de riesgo propuesto (IRP) y los registros de inundación en los años mencionados (IH).
En algunos municipios no coincide, esto se puede deber a que no se encontraron los registros de todos los municipios que presentaron problemas de inundación o que faltó considerar algunos otros factores que podrían aumentar el grado de vulnerabilidad o de costo.
Finalmente, se puede concluir que en general los factores incluidos en la construcción del índice fueron correctos, así como el uso de componentes principales para obtener las ponderaciones adecuadas para cada uno de los factores considerados.











 nueva página del texto (beta)
nueva página del texto (beta)