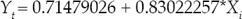Introducción
La disponibilidad de información hidroclimática en periodos superiores a los registros instrumentales (estaciones meteorológicas e hidrométricas) es fundamental para analizar la tendencia histórica y variabilidad de los caudales (Meko, Woodhouse, & Morino, 2012). En muchos casos, las estaciones hidrométricas son recientes y no cuentan con información extensa que permita estudiar la variabilidad del caudal de un río y por esa razón se recurre a métodos indirectos. Los anillos anuales de crecimiento de las coníferas representan un método indirecto para reconstruir la variabilidad histórica de los caudales y tomar decisiones respecto a los recursos hídricos (Brito-Castillo, Dı́az-Castro, Salinas-Zavala, & Douglas, 2003; Yuan et al., 2007; Yang, Qin, Shi, & Sonechkin, 2011).
Conocer la variabilidad del caudal es importante por su relación con la determinación de volúmenes para uso agrícola, generación de energía eléctrica, construcción de presas con fines de irrigación y estimación de caudales ecológicos, entre otros usos. La tendencia histórica de estos volúmenes, sin embargo, puede cambiar por factores antropogénicos o naturales, como su confinamiento en grandes reservorios, asentamientos humanos, extracción de material de construcción del lecho de las corrientes principales o variación en la precipitación (Shah, Bhattacharyya, & Chaudhary, 2014). Si a pesar de los cambios por actividad humana o fenómenos naturales las series de anillos anuales de los árboles registran una anchura proporcional a la precipitación y producción de agua, entonces es posible deducir la variabilidad natural de los caudales a partir de los anillos de crecimiento. Para conocer el comportamiento de un caudal en escala de un siglo o más es necesario el análisis conjunto de la información instrumental y de los anillos de crecimiento de los árboles (Villanueva-Díaz, Fulé, Cerano-Paredes, Estrada-Ávalos, & Sánchez-Cohen, 2009).
La regiones norte y centro de México, donde existen zonas boscosas de coníferas, son influenciadas en parte por patrones atmosféricos de circulación general que ocurren en el océano Pacífico (Seager et al., 2009). La Sierra Madre Occidental es la principal fuente de captación de agua en el norte de México y el recurso hídrico producido en las cuencas de este sistema montañoso drena hacia la altiplanicie del desierto chihuahuense en su vertiente oriental y hacia la planicie costera en su vertiente occidental (Descroix, González-Barrios, & Estrada-Avalos, 2004; Villanueva-Díaz et al., 2009). El sistema de tributarios del río Acaponeta representa una descarga de 1 350 hm3/año (Conaagua, 2008) y contribuye a la región conocida como “Marismas Nacionales” en los estados de Nayarit y Sinaloa, donde en su viaje al océano Pacífico los escurrimientos se conducen hacia 113 000 ha de manglares y estuarios, que por su alta biodiversidad vegetal y de fauna representan un área prioritaria de conservación RAMSAR.
La variabilidad de eventos con bajos (menos de una década) y largos (varias décadas) periodos de retorno (Fritts, 1976) del régimen hidrológico de los ríos vertientes a Marismas Nacionales es un factor que gobierna la dinámica de sus ecosistemas (De la Lanza, Carbajal-Pérez, Salinas-Rodríguez, & Barrios-Ordóñez, 2012). Es importante destacar, sin embargo, que en las últimas décadas, estos ríos han experimentado mayor variación en sus volúmenes de escurrimiento y en la calidad del agua, lo cual se atribuye al incremento poblacional, desarrollo agropecuario, confinamiento del agua y a la expansión de proyectos acuícolas para la producción de camarón (De la Lanza et al., 2012). Su comportamiento también se ha imputado a una mayor variabilidad hidroclimática reciente, que es evidente por eventos de sequía extremos que han afectado el norte de México (Villanueva-Díaz et al., 2011; Castruita-Esparza et al., 2016). No obstante, la presencia de sequías extremas en el norte de México todavía se ajusta a una casi periodicidad recurrente de 50 a 60 años, al menos en el último milenio.
El objetivo del presente estudio fue desarrollar una red de cronologías de ancho de anillo integradas por cuatro coníferas (Pinus durangensis, Pinus lumholtzii, Pinus leiophylla y Pseudotsuga menziesii) en las cuencas tributarias del río Acaponeta (CR-Acaponeta) y realizar una reconstrucción histórica del caudal medio de este río. Tal información es fundamental para conocer la variabilidad y tendencia del caudal en las últimas décadas, especialmente en lugares que carecen de información instrumental y, con base en reconstrucciones, sugerir estrategias para el manejo de recursos hídricos.
Materiales y métodos
Descripción del área de estudio
Los tributarios del río Acaponeta son Espíritu Santo, Tomadores, Zapota, Barbacoa, Tasajera y El Limón, que forman parte de la Región Hidrológica 11 (RH11) Presidio-San Pedro, cuyas principales corrientes descienden de la vertiente oeste de la Sierra Madre Occidental y desembocan al océano Pacífico (De la Lanza et al., 2012). La llanura de drenaje del río Acaponeta se integra por las corrientes Acaponeta y Cañas, las cuales desembocan en la laguna de Agua Brava, después de recorrer una distancia de 233 km, que es la longitud total del río. La cuenca del río Acaponeta cubre una superficie de 8 425 km2 y es la segunda en importancia dentro de Marismas Nacionales. La aportación media anual del río, acorde con la estación hidrométrica Acaponeta, es de 1 275 hm3 (millones de metros cúbicos) y de esta estación a la desembocadura, el volumen medio anual que se aporta es de 79.1 hm3, registrándose, por lo tanto, un volumen medio anual total de 1 353 hm3. El hidrograma de la estación Acaponeta se muestra en la figura 1.

Información tomada del Banco Nacional de Datos de Aguas Superficiales (BANDAS), Instituto Mexicano de Tecnología del Agua
Figura 1 Hidrograma de la estación hidrométrica Acaponeta para el periodo 1945-2011. Las barras corresponden al error estándar (n = 67).
El clima en la parte alta es templado sub-húmedo con lluvias de verano C(W2), con una temperatura media anual de 10 a 15 oC, y precipitación anual de 700 a 1 200 mm. El cociente precipitación/temperatura es mayor a 55, y la estacionalidad es tan marcada que la precipitación del mes más seco es menor a 40 mm y menor al 10% de la precipitación del mes lluvioso en verano. Gran parte del agua de escurrimiento se origina en los bosque mixtos de coníferas, destacando P. durangensis, P. cooperi, P. herrerae, P. leiophylla, P. lumholtzii y P. menziesii, aunque también se presentan varias especies de encinos (Quercus sp.) (García-Arévalo & González-Elizondo, 2003; González, González, & Márquez, 2007). La geología está conformado por roca ígnea extrusiva ácida principalmente y por roca sedimentaria; en los valles intermontanos se presentan depósitos aluviales. Las unidades de suelo de acuerdo con el sistema FAO (FAO-UNESCO, 1988) son litosol, cambisol y regosol (INEGI, 2005).
Ubicación de sitios de muestreo
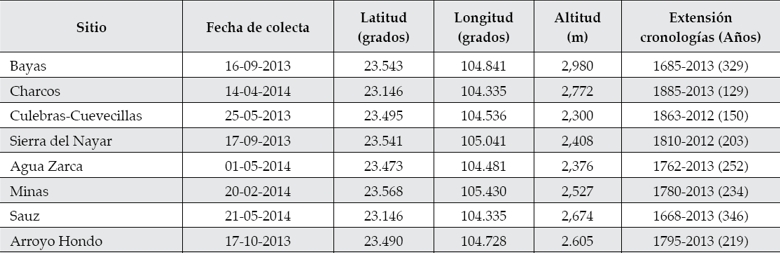
La ubicación de los ocho sitios de muestreo se muestra en la figura 2. La distancia máxima entre dos sitios se da entre Minas y Charcos, con 62 km. La composición arbórea de cada sitio de muestreo fue predominantemente P. durangensis, los cuales se distribuyen en la zona de producción de agua en las partes altas de las cuencas, que drenan hacia los tributarios del río Acaponeta. Aunque la especie principal que se muestreó fue P. durangensis, también se colectaron muestras de P. cooperi, P. herrerae, P. leiophylla, P. lumholtzii, P. menziesii.

Figura 2 Distribución de sitios de muestreo asociados con la parte alta de las cuencas tributarias del río Acaponeta.
Se eligieron sitios con el menor disturbio posible, buscando árboles que por su ubicación topográfica fueran de poca accesibilidad en el paisaje y que por esa razón no hubieran sido perturbados por el aprovechamiento forestal regulado o clandestinaje. A pesar de que estos árboles no están establecidos en los suelos más profundos y fértiles, sus series de anillos reflejan en forma confiable la dinámica de los eventos climáticos (Cleaveland, Stahle, Therrell Villanueva-Díaz, & Burns, 2003). El cuadro 1 muestra características generales de los sitios y la extensión de cronologías.
Cuadro 1 Características generales de los ocho sitios de colecta de muestras de anillos de crecimiento. La ubicación de los sitios es como se indica en la figura 1.
Muestras de anillos de crecimiento arbóreo
En cada sitio seleccionado se obtuvieron de dos a tres núcleos de crecimiento por árbol con un taladro de Pressler marca Haglöf de 6 mm de diámetro interno. La altura de extracción fue de 1.30 m sobre el nivel del suelo. En campo se colectaron entre 50 y 60 árboles. Sin embargo, el número de árboles fechados exitosamente por sitio fue de entre 40 y 45. De manera adicional, se colectaron secciones transversales de arbolado muerto o de tocones para incrementar el tamaño de muestra y extender las series en el tiempo.
Fechado y estandarización de las series
Las muestras se lijaron para el mayor contraste de los anillos y después se fecharon mediante técnicas dendrocronológicas convencionales (Stokes & Smiley, 1996; Fritts, 1976). El crecimiento radial se dividió en bandas de crecimiento de madera temprana (EW), tardía (LW) y anillo total (RW), las cuales se midieron con un sistema de medición VELMEX con precisión de 0.001 mm (Robinson & Evans, 1980).
El fechado, la respuesta común de crecimiento y la exactitud de la medición de los anillos se verificó con el programa Cofecha (Holmes, 1983; Grissino-Mayer, 2001). Las tendencias biológicas no relacionadas con clima se removieron mediante la estandarización con el programa Arstan (Cook, 1987), al ajustar la ecuación de mejor tendencia (exponencial o lineal negativas) a la serie de medición y dividiendo el valor real de ancho de anillo entre el valor predicho con la ecuación ajustada. De esta forma se generó un índice para cada banda, identificados como RWI, EWI y LWI, para ancho de anillo, madera temprana y madera tardía, respectivamente.
La cronología para cada localidad y banda se construyó con el promedio de los valores estandarizados de crecimiento (RWI, EWI y LWI) de todas las muestras de un mismo sitio (Fritts, 1976). La cronología estandarizada incluyó las versiones Estándar (Std), Residual (Res) y Arstan (Ars) (Cook, 1987). La primera versión deriva directamente de dividir el valor de medición entre el obtenido de la curva de ajuste; la versión Res se produce al eliminar o minimizar la autocorrelación, y la versión Ars se calcula al incorporar el valor de autorregresión a la cronología residual. El uso de una versión determinada en la reconstrucción de evento climático o historial de caudales depende del grado de correlación y significancia (Cook, 1987). En este caso, tomando en cuenta que los caudales son independiente de un año a otro, se trabajó con las versiones residuales en las que se minimiza la autocorrelación de un año a otro, como se sugiere en otros estudios de la literatura (Brito-Castillo et al., 2003). A los índices RWI, EWI y LWI de cada serie se les estimó una línea flexible suavizada (“spline”), calculada con intervalos de década, para resaltar eventos extremos (Cook & Peters, 1981).
Análisis estadístico
La asociación entre cronologías se analizó mediante un análisis de correlación y componentes principales (SAS, 2012), para determinar aquellas con una respuesta climática común e integrarlas a una cronología representativa de la cuenca con fines de comparación con variables climáticas e hidrométricas. Para mejorar la distribución normal de los datos de caudal medio se probaron transformaciones a valores logarítmicos, cuadráticos, raíz cuadrada y valor inverso. Los dos criterios para seleccionar la transformación fueron que se mejorara la distribución normal y la mayor correlación entre variables (Brito-Castillo et al., 2003).
Una vez que se demostró una correlación significativa entre datos transformados de caudal medio e índices de anillo, se seleccionaron las series residuales (RWIr y LWr), porque en estas series los valores de un año son menos influenciados por el año previo, como se espera que ocurra con los datos de caudal medio. Para encontrar la mejor ecuación lineal que explica la variación de caudal medio a partir de índice de anillo (RWIr y LWr), se usó la subrutina VERIFY de “Dendrochronology Program Library”, que identifica el periodo de máxima correlación entre variables y al mismo tiempo realiza una verificación en un subconjunto de los datos. Los dos criterios para seleccionar un modelo de reconstrucción fueron la correlación y el valor de reducción de error (Cook & Jacoby, 1983; Stahle & Cleaveland, 1992; Woodhouse, 2001). Aunque este procedimiento se enfoca en el periodo con máxima correlación, la ecuación seleccionada se usa sólo si en el proceso de verificación la correlación entre variables sigue siendo significativa y si la capacidad de predicción de la ecuación en intervalos fuera de los datos observados es significativa (Cook & Jacoby, 1983; Stahle & Cleaveland, 1992; Woodhouse, 2001).
La CR-Acaponeta se comparó con los índices ENSO para definir el impacto de este patrón circulatorio, el cual explica gran parte de la variabilidad hidroclimática invierno-primavera observada a nivel regional (Cleaveland et al., 2003; Cerano-Paredes, Villanueva-Díaz, Valdez-Cepeda, Méndez-González, & Constante-García, 2011; Villanueva-Díaz et al., 2011). Los índices ENSO reflejan un diferencial de temperatura de la superficie del mar en el Pacífico, comparado con la temperatura de las costas de Sudamérica; sus variaciones cíclicas, que ocurren en periodos entre tres y siete años, están relacionadas con la variación climática regional. Estos índices son de acceso libre en el sitio http://www.esrl.noaa.gov/psd/enso. La asociación con estos fenómenos circulatorios se realizó al contrastar tanto los índices dendrocronológicos individuales como el regional con índices registrados de El Niño Oscilación del Sur (ENSO) (Allan, Lindesay, & Parker 1996), índices SOI reconstruidos para el norte de México (Stahle, D’Arrigo, Krusic, & Cleaveland, 1998), y el índice de lluvia tropical (TRI), que constituye un estimativo de la variabilidad de ENSO y que se fundamenta en las anomalías de precipitación en la región del Pacífico Central, por lo que se le atribuye una mayor estabilidad que el índice de presión entre Tahití y Darwin, Australia (Wright, 1979). La razón de emplear índices generales de clima es porque los volúmenes de un caudal varían de acuerdo con la precipitación y, a su vez, la magnitud de la precipitación influye en el ancho de anillo (Margolis, Meko, & Touchan, 2011). La reconstrucción del caudal generado se verificó con reconstrucciones previas y documentos históricos relacionados con la producción de alimentos, y otros impactos sociales y económicos descritos para la región.
Resultados
El cuadro 2 muestra los indicadores dendrocronológicos de las ocho cronologías. La intercorrelación varió de 0.47 en Minas a 0.72 en Bayas. La sensibilidad media fluctuó de 0.137 en Minas hasta 0.288 Arroyo Hondo. Tanto la intercorrelación como la sensibilidad media aumentaron con la altitud, con correlaciones de 0.59 y 0.54, respectivamente; mientras que la autocorrelación decreció con la altitud (r = -0.69) (calculada con datos de los cuadros 1 y 2).
Cuadro 2 Indicadores dendrocronológicos para ocho cronologías y la cronología regional en la cuenca del río Acaponeta, Nayarit (CR-Acaponeta).

1Medición de la señal común de las series involucradas en una cronología; 2cambio relativo en el crecimiento de un año al siguiente (Fritts, 1976); 3grado de influencia que ejerce el año de crecimiento previo sobre el año de crecimiento actual; 4expresión de la intensidad de la señal común observada entre las series de una cronología; 5proporciona una estimación de la semejanza de una cronología fundamentada en un tamaño de muestras finito, con una generada con un tamaño de muestra infinito (Wigley, Briffa & Jones, 1984).
La mayoría de las series indicó una respuesta en crecimiento común por periodos, lo que podría deberse a la respuesta compartida ante la variabilidad climática regional (figura 3). Cuando se consideraron los datos promedio disponibles de precipitación (1968 a 2003), la correlación con RWI fue de 0.33 (n = 35, p < 0.05), lo que indica que la variación de acho de anillo está influenciada por la humedad. Algunos periodos aproximados de bajo crecimiento en los anillos de las especies estudiadas ocurrieron en las décadas de 1780, 1810, 1860, 1890, 1920, 1950, 1990 y 2010. Los periodos de buen crecimiento se presentaron en las décadas de 1820-1830, 1850, 1900, 1940, 1970 y 2000. La respuesta climática común captada por las series dendrocronológicas involucradas en el estudio indica que son afectadas por patrones climáticos a nivel geográfico.

Figura 3 Comparación de series de crecimiento de anillo total de cronologías desarrolladas con la inclusión de diversas especies de coníferas para sitios ubicados en el área de contribución de escurrimientos del río Acaponeta. Se indican algunos periodos aproximados de condición seca (flecha punteada) y húmeda (flecha continua). Los nombres de las cronologías son como se indica en el cuadro 3.
Debido a la asociación significativa entre todas cronologías del cuadro 3, éstas se integraron en una serie regional de madera temprana, tardía y de anillo total. La cronología regional de anillo total se extendió de 1684 a 2013, con un tamaño de muestra mayor a tres radios (n ≥ 4) después de 1686 hasta un máximo de 370 en el periodo más reciente, lo que implica que la serie dendrocronológica regional en gran parte de su extensión posee un tamaño de muestra confiable para captar la variabilidad hidroclimática del área de estudio (figura 4).
Cuadro 3 Correlación, significancia y tamaño de muestra (en paréntesis) entre cronologías.

BAY = bayas; CUC = culebras-cuevecillas; CHA = charcos; MIN = minas; AZA = agua zarca; SNA = sierra del Nayar; SAU= sauz; ARO = arroyo Hondo.

Figura 4 Cronología regional de anillo total, que representa las condiciones climáticas dominantes del área de contribución de la cuenca alta del río Acaponeta.
Aunque la cronología regional estuvo integrada por al menos cinco especies diferentes (P. durangensis, P. lumholtzii, P.cooperi, P. herrerae, P. menziesii) en sitios dispersos en el área de contribución del río Acaponeta, la cronología regional mostró una adecuada intercorrelación entre series que alcanzó 0.526, sensibilidad media 0.319 y autocorrelación de primer orden de 0.275 (datos no mostrados en cuadros). Estos valores constatan el buen potencial de la serie dendrocronológica para captar la señal climática regional. La concordancia de la varianza entre un tamaño de muestra finito y uno teóricamente infinito indicó que la intensidad de la señal (Signal Strentgh, SS, por sus siglas en inglés) con un valor superior a 0.8 se logró con ocho radios para el periodo de 1700 a 2013; por lo anterior, se eligió este lapso para analizar su relación con registros hidrométricos y generar un modelo con fines de reconstrucción hidroclimática.
Las cronologías regionales RWI, EWI y LWI se compararon con los datos transformados de caudal medio (m3 s-1) mensualmente y por periodos. Las correlaciones más altas que se obtuvieron con los datos hidrométricos d isponibles de 1946 a 2011 fueron entre la cronología de residuales de anillo total (RWIr) y el caudal medio de enero-agosto; y de la cronología de madera tardía (LWr), con el caudal de agosto-octubre (figura 4). Las correlaciones fueron bajas, pero significativas (figura 5). Sin embargo, la mayor correlación correspondió al periodo 1967-1994 (r = 0.74, p < 0.01, n = 26).

Figura 5 Relación entre valores transformados de caudal medio y las cronologías residuales de anillo total (a) y madera tardía (b).
Para generar el modelo de reconstrucción, los registros de caudal medio de 1967 a 1994, transformados a logaritmos, se dividieron en dos subperiodos: uno para calibración (1980-1994) y otro para verificación (1967-1979), los cuales mostraron correlaciones de 0.78 (p < 0.01) y 0.68 (p < 0.01), respectivamente (figura 6). Debido a que en ambos subperiodos la correlación es significativa, se utilizó la ecuación del periodo completo de 1967 a 1994 de registros hidrométricos disponibles para desarrollar el modelo de reconstrucción, el cual fue el siguiente:
Donde:
Yt |
= caudal reconstruido promedio (m3 s-1) en valores logarítmicos base10 del periodo estacional enero-agosto para la cuenca del río Acaponeta |
Xi |
= índice de anillo total de la versión residual de la cronología regional para un año determinado |

Figura 6 Subperiodo de calibración y verificación de la cronología regional de anillo total y el volumen caudal medio estacional enero-agosto de 1967 a 1994.
Aunque este procedimiento, mediante la subrutina VFY, se enfoca en el periodo con máxima correlación para generar una ecuación, ésta se considera si y sólo si en el proceso de verificación la correlación entre variables sigue siendo significativa. La reducción de error del modelo fue de 0.479, lo que corroboró la capacidad de predicción del modelo estadísticamente (Cook & Jacoby, 1983; Stahle & Cleaveland, 1992; Woodhouse, 2001).
Al aplicar el modelo lineal a la serie regional RWI se generaron los valores logarítmicos del caudal medio de enero-agosto para el periodo 1700 a 2013 (314 años); estos valores se transformaron mediante la función antilogarítmica para producir valores estimados del caudal medio estacional (enero-agosto) en m3 s-1 (figura 7).
Acorde con los datos hidrométricos instrumentales, el caudal medio enero-agosto de 1946 a 2011 fue de 33.16 m3 s-1, mientras que el de enero-junio alcanzó apenas 8.9 m3 s-1, pero se incrementó a 106 m3 s-1 en los meses de julio a agosto, lo que indica que es realmente el caudal del verano el que tiene mayor influencia en favorecer mayores gastos en el río Acaponeta. El gasto medio reconstruido enero-agosto en este estudio fue de 36.8 m3 s-1, 8.5% más que el caudal procedente de registros de la estación hidrométrica Acaponeta. Una comparación del comportamiento del caudal reconstruido del periodo 1700-2013 en subperiodos de 25 años indicó un comportamiento bastante estable, con dominancia de gastos en el intervalo de 34 a 37 m3 s-1 en 92% de los subperiodos; y sólo de 1725 a 1749 se tuvo un gasto promedio superior de 44 m3 s-1 (8%).
Dada la contribución a los escurrimientos de la precipitación de verano, la cronología residual de madera tardía se correlacionó significativamente con el caudal promedio agosto-octubre del periodo 1945 a 1976 (r = 0.703, p < 0.01) (figura 8). Este periodo se dividió en dos subperiodos: 1961-1976 para calibración (r = 0.69, p < 0.01) y 1945-1960 (r = 0.65, p < 0.01) para verificación. Debido a que ambos subperiodos fueron significativos y en la verificación presentaron una reducción de error positiva (ER), se utilizó el periodo 1945-1976 de registros hidrológicos disponibles para generar el modelo con fines de reconstrucción. El modelo utilizado fue el siguiente:
Donde:
Yt |
= flujo histórico reconstruido promedio (m3 s-1) en valores de gasto en raíz cuadrada del periodo estacional agosto-octubre para la cuenca del río Acaponeta |
Xi |
= índice de madera tardía de la versión residual de la cronología regional para un año determinado |

Figura 8 Relación entre la cronología residual de madera tardía y el caudal medio de agosto-octubre, 1945-1976.
De igual manera que con la ecuación anterior, la reducción de error fue significativa, con un valor de 0.465, y la correlación de los datos usados para calibración y verificación fue significativa. Al aplicar el modelo lineal a la serie regional de madera tardía se generaron los valores en raíz cuadrada de escurrimiento promedio agosto-octubre para el periodo 1700 a 2013 (314 años); estos valores, al elevarlos al cuadrado, se transformaron para producir gastos reconstruidos de escurrimiento promedio estacional en m3 s-1 (figura 9).

Figura 9 Caudal medio reconstruido agosto-octubre con la cronología residual de madera tardía para el río Acaponeta, Nayarit.
Gran parte de los escurrimientos se presentan durante el verano, con un gasto promedio del periodo agosto-octubre de 115 m3 s-1, en comparación con el gasto promedio de enero-julio, que es de sólo 19.4 m3 s-1, y el de noviembre-diciembre de 13.2 m3s-1; por lo anterior, a fin de analizar periodos reconstruidos de mayor o menor gasto interanual y multianual, se puso mayor énfasis en describir la variabilidad hidroclimática de verano en contraposición con la de invierno-primavera, que es menor y tiene mayor influencia de fenómenos circulatorios como ENSO. De esta manera, se detectaron periodos secos y húmedos de 2 a 10 años consecutivos (cuadro 4).
Cuadro 4 Años reconstruidos con la ocurrencia de periodos secos y húmedos con base en la reconstrucción del gasto medio agosto-octubre en el río Acaponeta, Nayarit.

1 Un año seco es aquel con un gasto reconstruido inferior al gasto medio reconstruido (116.3 m3s-1) y para un año húmedo el gasto es mayor a dicho valor.
Los episodios con menor escurrimiento promedio en el verano ocurrieron en los periodos 1771-1779 (77 m3 s-1); 1866-1873 (81m3 s-1); 1949-1957 (91 m3 s-1); 1974-1976 (80 m3 s-1), y 1994-2000 (77 m3 s-1), y aquellos con mayor escurrimiento de 1734 a 1739 (153 m3 s-1); 1791-1794 (155 m3 s-1); 1831-1835 (140 m3 s-1); 1852-1853 (127 m3 s-1); 1940-1942 (140 m3 s-1), y 1983-1985 (173 m3 s-1), aunque años con valores extremos tanto secos como húmedos fueron comunes; es decir, los años con bajo gasto promedio de 1730, 1785, 1805, 1893, 1957, 1991, 2011, y los años húmedos de 1706, 1723, 1734, 1791, 1901, 1905, 1983, 1985 y 2010.
Al comparar la reconstrucción del caudal de río Acaponeta con volúmenes reconstruidos de escurrimiento para la cuenca del río Yaqui (Villanueva-Díaz et al., 2014), se encontró una correlación moderada, pero estadísticamente significativa entre ambas reconstrucciones (r = 0.39, p < 0.01, 1700-2013), lo que indica la viabilidad de las cronologías de anillos de crecimiento en una escala regional. Aunque la correlación es baja, los datos indican correlación entre los volúmenes de caudal, que su vez están determinados por la variabilidad de precipitación de un año a otro (figura 10). En promedio, los volúmenes del caudal del río Yaqui son 63% de los del río Acaponeta.

Figura 10 Caudal reconstruido del río Valle del Yaqui y de río Acaponeta. La línea sólida representa la relación 1:1 y la línea punteada corresponde a la ecuación.
En particular, hay coincidencias en los periodos 1750-1800 y 1920-1950, y en las últimas cinco décadas hay un desacople de eventos entre los dos lugares. Dicha relación sugiere una influencia común de fenómenos circulatorios de amplio impacto, ya que la distancia entre sitios representativos de ambas regiones es de 700 km en línea recta. Los periodos secos coinciden en frecuencias aproximadas de 50 a 60 años, comportamiento que ha sido reportado en reconstrucciones previas para el norte de México (Cleaveland et al., 2003; Cerano-Paredes et al., 2011; Villanueva-Díaz et al., 2011; Castruita-Esparza et al., 2016).
Una parte importante de la variabilidad climática en el norte de México se explica por el fenómeno de El Niño Oscilación del Sur (ENSO, por sus siglas en inglés), en particular durante su fase cálida, que se caracteriza por un incremento en la precipitación invernal (Stahle et al., 1998; Stahle et al., 2012). Al comparar los índices de la cronología regional RWI e índices del SOI, como los generados por Allan, Lindesay y Parker (1996); National Climatic Data Center (NOAA, 2014); índice de lluvia tropical (TRI, por sus siglas en inglés) (Wright, 1979); índice multivariado de ENSO (MEI) (NOAA, 2014), y los reconstruidos para el norte de México (Stahle et al., 1998), se encontró una asociación significativa entre RWI e índices estacionales de la literatura (cuadro 5). En general, la correlación encontrada entre los índices de anillo total de la cronología regional residual fue superior a -0.5, lo que indica una relación inversa entre los índices SOI y el valor del índice de ancho de anillo. La asociación fue positiva con los índices TRI y MEI, pues el primero considera la cantidad de lluvia en mm y el índice MEI tiene revertidos los signos con valores positivos durante la fase El Niño y negativos durante La Niña, no obstante que el fenómeno que se analiza es el mismo.
Cuadro 5 Relación entre la cronología regional CR-Acaponeta y los índices estacionales promedio SOI del periodo invierno-primavera.

1 SOI reconstruido (diciembre-febrero): índices SOI reconstruidos derivados de los primeros cuatro componentes principales de una red dendro-cronológica de Norteamérica y de Java, Indonesia, que explican 53% de la varianza del SOI en el periodo invernal (diciembre-febrero) (Stahle et al., 1998); 2Allan SOI invernal (diciembre-febrero): índices de SOI basados en la diferencia de presión de la temperatura de agua del mar entre las islas de Tahití y Darwin, Australia, y que considera las anomalías de la diferencia de la medias normalizada de las series en desviaciones estándar (x10) para el periodo 1876-1996 (Allan et al., 1996). 3TRI: índice de lluvia tropical, constituye una estimación de la variabilidad de ENSO, al fundamentarse en las anomalías de precipitación en la región del Pacífico central, lo que le da una mayor estabilidad que el índice Tahití-Darwin (Wright, 1979); 4MEI: índice multivariado de ENSO, que se fundamenta en seis variables registradas en el Pacífico Tropical, las cuales son presión al nivel del mar (P), componentes del viento superficial tanto zonal (U) como meridional (V), temperatura del agua superficial del mar (S), temperatura del aire (A) y fracción total de nubosidad del cielo (C). EL MEI se obtiene de manera separada al integrar las variables de manera bimestral (diciembre-enero, enero-febrero, etc.). El MEI se calcula como el primer componente sin rotación (PC), al combinar las seis variables señaladas (Wolter & Timlin, 2011). Con este índice, valores negativos MEI representan la fase fría (La Niña) de ENSO y positivo, la fase cálida (El Niño).5SOI enero-abril es el índice que considera diferencia de presión en el océano Pacífico, en particular entre las islas de Tahití y Darwin. Valores negativos sostenidos por debajo de -8 indican episodios de El Niño (Allan et al., 1996).
La mejor relación encontrada entre los diversos índices SOI y los índices de anillo total fue la obtenida entre los índices SOI invernal (Allan et al., 1996) y la cronología CR-Acaponeta; situación que corrobora el efecto favorable de este fenómeno, al incrementar la precipitación del periodo invernal en dicha región (figura 11).

Figura 11 Relación entre la cronología regional, versión residual (RWIr) y el índice SOI del periodo invernal (de acuerdo con Allan, Lindesay, & Parker, 1996). La relación es negativa, pues mientras los SOI se tornan negativos (años El Niño), el crecimiento del anillo total se incrementa; caso contrario ocurrió en años La Niña, donde el crecimiento se redujo debido a sequías severas.
La relación observada fue particularmente alta (r = -0.76, p < 0.01, n = 61) durante años intensos de El Niño/La Niña, donde se observó que a menor valor de este índice, se presentó un incremento en el índice de anillo total asociado con un aumento en la precipitación y, por ende, en el gasto promedio; este comportamiento se presentó en más del 90% de los años con valores negativos SOI, entre algunos de ellos se encuentran los años de 1919 (-13.42), 1941 (-17.12), 1978 (-15.12), 1981 (-16.52), 1983 (-31,12), 1992 (-19.32); caso contrario ocurrió en años con dominancia de la fase fría (La Niña) de valores positivos SOI, donde el valor del índice de ancho de anillo fue inferior al promedio, como ocurrió en 1879 (13.88), 1910 (16.98), 1929 (14.18), 1951 (12.98), 1971 (10.88), 1974 (16.88) y 1989 (9.68). La alta asociación entre el crecimiento radial de las especies arbóreas en la cuenca del río Acaponeta y los índices SOI sugieren que esta región es sensible a la influencia de ENSO en su fase cálida y fría, respectivamente. Esta información es relevante para un mejor entendimiento de la variación interanual y multianual ocasionada por este fenómeno circulatorio, el cual, gracias a su monitoreo constante en el Pacífico tropical puede ser predicho con meses de antelación, en particular sus eventos extremos (Jin et al., 2008).
Discusión
Integración de la cronología única
Este estudio demuestra que la integración de una red regional y confiable a partir del muestreo de árboles establecidos en la parte alta de la cuenca es posible. Las cronologías de diferentes especies mostraron una señal de crecimiento común. El hecho de que la intercorrelación y sensibilidad de la cronología se incremente con la altitud indica que las especies de mayor distribución altitudinal registran con mayor intensidad los cambios en humedad; sin embargo, a mayores altitudes, la autocorrelación aumenta, indicando que el agua almacenada en el perfil del suelo del año previo es más importante en mayores altitudes que en las partes bajas donde los árboles pueden aprovechar el escurrimiento superficial (Castruita-Esparza et al., 2016). Esta información es congruente con los valores de EPS > 0.85 que requieren de 17 árboles, es decir, dos tercios más que en mayores altitudes.
Corroborar el potencial de las series de anillos para comprender la variación de los caudales es importante. En el norte de México se ha podido explicar la dinámica de caudales con anillos de crecimiento empleando cronologías de anillos separadas más de 300 km (Brito-Castillo et al., 2003). En este caso, la distancia entre las cronologías no es mayor que 100 km. La integración de redes dendrocronológicas a nivel de subcuenca, cuenca o región hidrológica se ha usado con frecuencia para entender de mejor manera la variabilidad hidroclimática histórica que caracteriza una región y para generar reconstrucciones de flujo representativas de los principales tributarios que se alimentan del agua generada en las partes altas de las cuencas forestadas (Villanueva-Díaz et al., 2005; Woodhouse, Stahle & Villanueva-Díaz, 2012). Para integrar una serie dendrocronológica representativa de una región, las series individuales deben mostrar una variación interanual y multianual similar; en este caso, los índices de las diversas cronologías distribuidas en el área de captación y producción de agua del río Acaponeta mostraron una asociación común y estuvieron correlacionadas significativamente entre sí, de tal forma que al integrarlas en una cronología regional, ésta constituyó un “proxy” confiable de las condiciones hidroclimáticas dominantes en toda el área de captación y producción de agua.
Dos factores que debieron haber contribuido a encontrar una correlación alta (0.70) y significativa en las salidas del caudal Acaponeta y los anillos de crecimiento son, por un lado, el hecho de que la Sierra Madre Occidental es un complejo fisiográfico con clima templado estable en la parte alta; por otro lado, la rápida respuesta de crecimiento de las coníferas a la precipitación y temperatura permite la definición clara de anillos de crecimiento. Cuanto más definida es la fisiografía y el clima, los anillos de las coníferas registran con mayor fidelidad los cambios de clima. Por ejemplo, en la región del Himalaya, Larix griffithiana explicó hasta el 61% de la variabilidad del río Lachen en los últimos 300 años (Shah, Bhattacharyya, & Chaudhary, 2014). En el noreste de China, ocho cronologías de Picea schrenkiana separadas 80 km explicaron el 51% de la variación del caudal del río Manasi, con una señal común por casi 400 años (Yuan et al., 2007). Una cronología compuesta por Austrocedrus chilensis y Pilgerodendron uviferum explicó 42% de la variación del caudal del río Puelo (diciembre-mayo) en Chile, con una extensión de 400 años; la distancia entre sitos fue de hasta 150 km (Lara, Villalba, & Urrutia, 2008). Para el río Santa Fe, una cronología combinada de Pinus edulis y Pseudotsuga menziesii, con separación de sitios dentro de los 100 km, logró una correlación de 0.50 y 0.62 para explicar la dinámica del caudal a partir de la cronología en el corto y largo plazos, respectivamente; el alcance de la cronología fue de 700 años (Margolis, Meko, & Touchan, 2011).
La partición del anillo total en bandas de madera temprana y tardía tiene la ventaja comparativa de que se pueden generar reconstrucciones de escurrimientos y de variables climáticas estacionales, como precipitación invierno-primavera con madera temprana y anillo total (Panshin & Zeeuw, 1980; Cleaveland et al., 2003), y precipitación de verano con madera tardía (Griffin, Meko, Touchan, Leavitt, & Woodhouse, 2011). Para el caso de la cronología regional de madera temprana y de anillo total en el río Acaponeta, éstas respondieron al gasto medio escurrido enero-agosto, que cubre el periodo estacional invierno-primavera e inicio del verano; mientras que la cronología de madera tardía se relacionó más con el gasto promedio de verano y principios de otoño. El análisis comparativo entre ambas reconstrucciones proporciona una idea más clara de la variabilidad estacional del gasto disponible en el río Acaponeta y de los fenómenos circulatorios que lo afectan.
Dinámica del caudal medio
El caudal reconstruido agosto-octubre en m3 s-1 y transformado en millones de metros cúbicos (Mm3) o hectómetros cúbicos (hm3) fue del orden de 905 hm3, lo que constituye casi 70% del volumen de escurrimiento anual del río Acaponeta, estimado en 1 336 hm3 para los últimos 50 años, y que se ha utilizado para estimación de gastos ecológicos y dotación de volúmenes con fines de riego (De la Lanza et al., 2012). El volumen reconstruido, aunque mostró fluctuaciones de alta y baja frecuencia en los últimos 314 años, con un rango de 1 425 hm3 (valor mínimo de 281 hm3 y máximo de 1 706 hm3), podría estar sugiriendo una reducción en el gasto medio estacional agosto-octubre de 981 hm3 en el periodo 1700-1749 a 890 hm3 de 1949 a 1999, y en las últimas dos décadas se redujo un 10%. Sin embargo, es importante señalar que a pesar de esta tendencia, se requiere de más observaciones, pues los datos de dicho estudio indican que la variación en los caudales estacionales y anuales oscila entre 30 y 40%; y además, después de la década de 1970, la variación se ha incrementado (Brito-Castillo et al., 2003).
Aunque en apariencia no existe presión por el agua en la cuenca, los cambios de uso del suelo debido a una explotación forestal intensiva tienen el potencial de conducir a la reducción en el flujo base, como ha ocurrido en otras cuencas aledañas del estado de Durango en la Sierra Madre Occidental (Estrada, Villanueva & Trucios, 2013), aunado a un incremento en granjas acuícolas, particularmente para la explotación de camarón, que demandan volúmenes constantes y adicionales de agua para su explotación (De la Lanza et al., 2012), lo cual influye en la reducción de los gastos registrados en la estación hidrométrica del río Acaponeta. Es muy importante aclarar que los resultados de este estudio no deben tomarse como concluyentes para demostrar la reducción del caudal de manera reciente, pero sí pueden ser un indicio para probar esta hipótesis con un estudio más integral y anticiparse a problemas de manejo de los recursos hídricos en el río Acaponeta.
Relación con eventos circulatorios globales
De manera natural, la fluctuación en la variabilidad hidroclimática en el norte y noroeste de México es mayor en la época invierno-primavera debido a la influencia de ENSO; mientras que en el verano, la influencia del monzón de Norteamérica o mexicano es menor, y la variabilidad interanual es mínima, como se ha demostrado para la cuenca del río Yaqui en Sonora (Nicholas & Battisti, 2008); así, para analizar la variabilidad histórica del flujo invierno-primavera en la cuenca del río Acaponeta, la reconstrucción de gasto enero-agosto proporciona una base de datos ideal para este tipo de análisis, así como para fundamentar de mejor manera gastos ecológicos, cuya limitante es la disponibilidad de registros hidrológicos extensos que permitan disponer de información de la variabilidad hidroclimática para estimaciones de volúmenes ecológicos en diversos escenarios (De la Lanza et al., 2012).
La influencia de ENSO en el noroeste y norte de México tiene un impacto muy similar, como se demuestra con estudios hechos en toda esta región (Stahle et al., 1998; Nicholas & Battisti, 2008; Cerano-Paredes et al., 2011; Meko et al., 2013). No obstante, es importante analizar con detalle el grado de impacto y variabilidad hidroclimática producida en ciertas regiones hidrológicas, y definir las causas potenciales que originan dicha variación.
Conclusiones
Las cronología de especies de coníferas, como P. durangensis, P. menziesii, P. cooperi, P. herrerae y P. lumholtzii muestran una señal común a pesar de una separación de unos 70 km. Los resultados indican que validando las cronologías de la Sierra Madre Occidental se puede lograr la reconstrucción histórica de caudales.
La serie regional de índice de anillo total, madera temprana y tardía estuvo sustentada por un número de núcleos que alcanzó un tamaño de muestra de ocho radios a partir de 1700 y se incrementó a más de 370 radios en la parte final de la cronología. Este resultado muestra el poder de reconstrucción de los caudales con una muestra relativamente pequeña de árboles, siempre que sea posible identificar la señal común de éstos y su intercorrelación con otros sitios en una misma fisiografía.
La serie regional de madera tardía estuvo significativamente correlacionada con el gasto promedio del periodo estacional y se desarrolló una reconstrucción del mismo del periodo 1700-2013. El gasto agosto-octubre fue más estable que otros y es de gran importancia hidrológica, pues los volúmenes representan casi el 80% del volumen total anual.
La alta relación encontrada entre los índices regionales de anillo total y madera temprana con los índices SOI de invierno indica que esta región tiene alta sensibilidad a las fases cálida y fría de ENSO, y la respuesta en crecimiento radial de las coníferas en estudio supera una correlación de 0.75 para eventos intensos El Niño/La Niña.
No obstante que la red dendrocronológica se integró por ocho series dendrocronológicas, es importante ampliar la red y extender las series de tiempo para generar información más extensa de las fluctuaciones hidroclimáticas que caracterizan la captación y producción de agua en otras regiones del país. Aunque los resultados de este estudio no deben tomarse como concluyentes para demostrar la reducción del caudal del río Acaponeta en las últimas décadas, los hallazgos de este estudio indican la necesidad de probar esta hipótesis con un análisis más integral y anticiparse a problemas de manejo de los recursos hídricos en el río Acaponeta.











 nueva página del texto (beta)
nueva página del texto (beta)