Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Tecnología y ciencias del agua
versión On-line ISSN 2007-2422
Tecnol. cienc. agua vol.9 no.2 Jiutepec mar./abr. 2018 Epub 24-Nov-2020
https://doi.org/10.24850/j-tyca-2018-02-09
Notes
Quantification with SPEI of historical Droughts and under probable climatic change in the climatological station Zacatecas, Mexico
1Profesor Jubilado de la Universidad Autónoma de San Luis Potosí. San Luis Potosí, México.
The SPEI (Standardized Precipitation-Evapotranspiration Index) is a variant of the widespread SPI (Standardized Precipitation Index), it has greater potential as drought index since it is sensitive to climate change because it uses a more realistic measure of the water availability: the climate balance. This measure is evaluated by the difference between monthly precipitation and potential evapotranspiration. This study describes in detail the calculation of SPEI and its application to the monthly historical records of precipitation and average temperature available in the climatological station Zacatecas, located in the capital of the state of Zacatecas, Mexico. The data covers 86 years in the period from 1930 to 2015. For historical droughts, the results of SPEI indicate in light, moderate, severe and extreme droughts, the following approximate values: 32.2%, 11.5%, 5.0% and 1.3%. For this particular location, three scenarios of climatic change were proposed; the first one accepts a progressive and linear reduction of 20% in annual precipitation, the second one adopts a progressive and linear increase of 4 °C in the average temperature and finally, the third one, superimposes the two effects mentioned; being therefore the most critical. For the three proposed scenarios, results suggest that light and extreme droughts increase scarcely in number or percentage, and that moderate and severe droughts decrease, also in a slight way. Results are condensed on graphs of SPEI evolution of duration 12 months, historical and the third scenario, in which the times of occurrence of drought periods are clearly displayed, as well as the specific differences in the value of SPEI exposed. Based on these analyzes, the systematic application of SPEI in the characterization of historical and future droughts is recommended, its application on future droughts would lead to results merely indicative.
Keywords SPEI index; Log-Logistic distribution; probability weighted moments; potential evapotranspiration; statistical homogeneity; climate change
El SPEI (Standardized Precipitation-Evapotranspiration Index) es una variante del ampliamente difundido SPI (Standardized Precipitation Index), que tiene un mayor potencial como índice de sequías al ser sensitivo al cambio climático, debido a que usa una medida más real de la disponibilidad de agua, el balance climático. Esta medida se evalúa con la diferencia entre la precipitación y la evapotranspiración potencial mensuales. En este estudio se describe con detalle el procedimiento operativo del SPEI y se aplica a los registros históricos mensuales disponibles de precipitación y temperatura media en la estación climatológica Zacatecas, ubicada en la capital del estado de Zacatecas, México, los cuales abarcan 86 años (1930-2015). Para las sequías históricas, los resultados del SPEI definen en las sequías leves, moderadas, severas y extremas, los valores aproximados siguientes: 32.2%, 11.5%, 5.0% y 1.3%. Para esta ubicación del país, se consideró conveniente formular tres escenarios del cambio climático, el primero acepta una reducción progresiva y lineal del 20% en la precipitación anual, el segundo adopta un aumento progresivo y lineal de 4°C en la temperatura media anual y el tercero, sobrepone los dos efectos citados; por lo tanto es el más crítico. En los tres escenarios planteados, se encuentra que las sequías leves y extremas aumentan someramente en número o porcentaje y que las sequías moderadas y severas disminuyen, también de manera mesurada. Se exponen los gráficos de evolución del SPEI de duración 12 meses, histórico y del tercer escenario, en los cuales se visualiza claramente las épocas de ocurrencia de los periodos de sequía, así como de las diferencias puntuales en el valor del SPEI. Con base en los resultados de estos análisis, se recomienda la aplicación sistemática del SPEI en la caracterización de las sequías históricas y futuras. En estas últimas, los resultados tienen únicamente un carácter orientativo.
Palabras clave índice SPEI; distribución Log-Logística; momentos de probabilidad ponderada; evapotranspiración potencial; homogeneidad estadística; cambio climático
Introduction and Objective
Droughts are one of the main natural causes of damage to agriculture, to all economic activities and to the environment. Droughts occur after long periods of low precipitation and due to their slow evolution, it is difficult to specify their beginning and end, as well as to estimate their characteristics of magnitude, duration and territorial extent. On the other hand, due to the sustained growth of water demand for all uses and the threat of the climate change, in recent years the study of droughts has been intensified (Mishra & Singh, 2010; Vicente-Serrano, Beguería, & López-Moreno, 2010).
As droughts are a natural phenomenon and threat, their best characterization is carried out using indicators which are climatic, hydrological, agricultural and/or socio-economic variables showing numerically the potential of droughts regarding the deficiencies and damages that they produce. A drought index is a method based on statistical calculations using indicators and seeks to quantify droughts, thereby enabling their comparison in climates and dissimilar hydrological regimes; also favor the development of correct and efficient mitigation actions of their negative impacts (Mishra & Singh, 2010; Fuchs, Svoboda, Wilhite, & Hayes, 2014).
Another important aspect of droughts is their character of multiple time scales (multiscaler), which is caused by the delays that occur in the use of water in the different hydraulic systems, so that deficiencies in precipitation are first visible in temporary agriculture, then in irrigation supply, hydroelectric power generation and other water uses, and finally, in social, economic and environmental impacts. Due to the above, droughts are classified as: meteorological, agricultural, hydrological and socio-economic. The latter include environmental damage (Pandey, Sharma, Mishra, Singh, & Agarwal, 2008; Vicente-Serrano et al., 2010; Fuchs et al., 2014).
Since the end of the last century, drought studies and the development of their warning and monitoring systems have been based on the PDSI (Palmer Drought Severity Index) and SPI (Standardized Precipitation Index); the first one based on a soil moisture balance (Palmer, 1965; Wells, Goddard, & Hayes, 2004) and the second in a probabilistic approach of precipitation (McKee, Doesken, & Kleist, 1993; Wu, Svoboda, Hayes, Wilhite, & Wen, 2007). The PDSI has been criticized for not having multiscalar character in the time nor a simple calculation, besides not being sufficiently sensitive to induced changes in precipitation and temperature. The SPI has shown an efficient use of the available information and its main criticism is to use only monthly precipitation data, thereby ignoring other indicators of drought, such as temperature and potential evapotranspiration.
Since droughts are a complex and natural phenomenon with wide impacts, their characterization has recently been sought through indices based on multiple variables. Hao and Singh (2015) describe the various approaches to constructing multivariate indices, among the best known are the use of the soil water balance and the latent or hidden variables. A hidden variable is formed with a difference or quotient of variables that have great physical significance in drought; for example, precipitation and potential evapotranspiration, and thus the RDI (Reconnaissance Drought Index) was proposed with the quotient of such variables (Tsakiris & Vangelis, 2005; Campos-Aranda, 2015) and the SPEI (Standardized Precipitation-Evapotranspiration Index) with its difference, which implies a condition of water deficit or excess. The SPEI is a new drought index proposed by Vicente-Serrano et al. (2010) and Beguería, Vicente-Serrano, Reig and Latorre (2014) of calculation similar to the SPI, which is multiscalar and sensitive to induced alterations in the historical records of precipitation and temperature, according to the expectations presented by the climate change in such zone or region. An application of the SPEI with such approach has been exposed by Törnros and Menzel (2014) for a zone of Middle East.
The objective of this study is to describe in detail the operational procedure of the SPEI and to apply it to the available historical record of precipitation and average temperature of the climatological station Zacatecas, located in the capital city of the same name of the state of Zacatecas, Mexico. This record covers 86 years in the span of 1930 to 2015. Nine durations of drought ranging from 3 to 48 months are processed and three scenarios are analyzed for the probable climate change, the first considers a progressive and linear reduction that reaches 20% of the annual precipitation, the second adopts a progressive and linear increase that reaches 4°C in the average annual temperature and the third, the most critical, combines the negative effects of both alterations. Based on the percentages defined by SPEI for light, moderate, severe and extreme droughts, the contrast of results are made and the conclusions are formulated.
Summary of the Operational Theory
SPEI calculation
The SPI has been applied using various durations k of droughts, which varied from three to 72 months (Vicente-Serrano et al., 2010). The monthly precipitation record is processed under the moving sum scheme, so that for the duration of 3 months, the first sequence is obtained by adding the historical data one, two and three, the second sequence is the sum of the data two, three and four and so on until the last sequence, which is made up of the antepenultimate, penultimate and last data. Then the number of ns sequences that can be formed depends on k and is defined by expression:
in which, NA (for its Spanish initials) is the number of completed years of the processed record (> 30 years). The fundamental difference between the calculation of SPI and SPEI is that the second uses as historical data the differences (D j,i ) between the monthly precipitation (P j,i ) and the monthly potential evapotranspiration (ETP j,i , for its Spanish initials), that is:
Logically, j varies from one to 12 and i
from one to NA. In order to proceed with the calculation of the SPEI,
firstly, the sequences of differences designated by
being:
In equation 3 the sequences
are used ordered in increasing form
being, γ > 0, α > 0 and u < x mo the parameters of form, scale and location. x mo is the minimum sequence observed. The values of the fitting parameters are estimated with the following expressions (Haktanir, 1991):
in which Γ (·) is the Gamma factorial function, it was estimated with the formula of Stirling (Davis, 1972):
Calculated the three fit parameters (γ, α, u) of each duration
k analyzed, equation 5 is applied with x =
Monthly ETP calculation
Mavromatis (2007) found that the use of simple or complex methods for estimation of ETP j,i , leads to similar results when applying drought indices such as that of Palmer. Based on this result, Vicente-Serrano et al. (2010) adopt a simple approach to estimate the ETP j, i , through the Thornthwaite formula, whose expression is:
in which, Fc is a corrective factor function of the latitude of place (LAT) and of number of days in the month (ndm), its formula is:
where, N is the maximum sunshine or maximum number of hours with average monthly sun. For its estimation in the Mexican Republic, Campos-Aranda (2005) developed the following empirical expression:
where nm is the number of month, with 1 for January and 12 for December; A and B are constants function of LAT in degrees, with the following expressions:
Tt j,i is the average monthly temperature in °C and IC i is an annual heat index, equal to the sum of the 12 monthly indices, which are:
Finally, the exponent m is function of IC i with the following empirical equation:
values of Tt j,i higher than 26.5 °C there is no influence of IC i , so ETP j,i is only function of Tt j,i and is tabulated in Campos-Aranda (2005).
Hypothetical scenarios of climate change
Vicente-Serrano et al. (2010) and Ma et al. (2014) have suggested that as a consequence of climate change processes, at least two scenarios must be studied, the first is a reduction in precipitation and the second, an increase in average temperature. Based on quantitative analyses done by these authors and the climatic projections for Mexico by Montero, Martínez, Castillo and Espinoza (2010), three scenarios were established for analysis: (1) a progressive and linear reduction of 20% in annual precipitation of the historical record; (2) a progressive and linear increase of 4 °C in the average annual temperature record and (3) the superimposition of both changes in the historical record. The changes mentioned have a direct impact in the severity and duration of droughts (Fuchs et al., 2014). The correction of the monthly precipitation record (PM j,i ) is made based on the following equation:
in which, Δ P is the slope of reduction and therefore equals to the quotient of 0.20 between the number of years NA and i is the year counter, ranging from 1 to NA. The average monthly temperature correction (TM ij ) is carried out with equation:
now, ΔT is the slope of the increase and therefore equal to the quotient of 4 °C between NA.
Processed data and their Results
Historical records available
The climatological station Zacatecas is located in the city of the same name, which is the capital of the state of Zacatecas, Mexico, which according to historical information provided by the Local Office of the National Water Commission (CONAGUA), has operated continuously and has not undergone changes of location, so the records can be considered reliable. Its geographical coordinates are as follows: latitude 22° 45' N, longitude 102° 34' W.G. and altitude 2485 m.a.s.l. Its available monthly precipitation (mm) records and average temperature (°C) in the Excel files of CONAGUA of Zacatecas, started in January 1953 and are available until December 2015, with missing data in April 1986 and several months of the years 2010 to 2013.
The first missing data were adopted equal to the monthly averages and the rest was considered equal to the values recorded in the same months in the climatological station Guadalupe, which is approximately 6 km in a straight line and is located inside of the same geographical sub-region. This was considered acceptable due to the similarity that both records show at annual level, both in precipitation and in average temperature. On the other hand, in the Climatological Bulletin No. 3 (SARH, 1980) of the Hydrological Region No. 37 (El Salado), the available records of the Zacatecas station of the monthly precipitation and average temperature begin in January of 1930 and go up to December of 1978. Then, the period from January 1930 to December 1952, without missing data, was taken from such Bulletin and with it a joint record of NA = 86 years was integrated. The twelve monthly average values of the integrated precipitation record are: 16.2, 9.6, 5.7, 7.5, 17.7, 80.0, 102.1, 97.9, 85.4, 35.4, 12.8 and 12.0, whose sum is 482.2 mm, magnitude corresponding to the average annual precipitation. Values of the average monthly temperature record are: 11.7, 12.7, 14.8, 17.1, 19.0, 19.0, 17.5, 17.6, 17.0, 16.1, 14.1 and 12.3, with an annual average value of 15.7 °C.
Homogeneity tests
Starting from the monthly historical records, the annual values of precipitation and average temperature were integrated, to which three basic tests (Helmert, Sequences and Von Neumann) and six specific ones were applied: two of persistence (Anderson and Sneyers), two of trend (Kendall and Spearman), one of them of change in the variability (Bartlett) and another of change in the mean, that of Cramer. These tests can be consulted in WMO (1971); Campos-Aranda (2005), and Machiwal and Jha (2012).
The annual precipitation record is perfectly homogeneous, since no general or specific test detected any deterministic components. On the other hand, the mean annual temperature record was not homogeneous because, according to the basic and specific tests, shows persistence and change in mean. This evidence of lack of homogeneity justifies the approach of scenarios related to climate change.
SPEI values with the historical records
For this study it was decided to analyze the following nine durations k of droughts: 3, 6, 9, 12, 18, 24, 30, 36 and 48 months. In Table 1 the results obtained with available historical records were concentrated for each duration according to four concepts: (1) those related to the statistical properties of the sequences formed, (2) those corresponding to the fitting of the Log-Logistics distribution, (3) those associated with the statistical indicators of SPEI and (4) those belonging to the defined drought types.
The first group of results gives an idea of the variability and bias of the sequences formed with the criterion of moving sums; in such a way that the second group, which are the fit parameters of the distribution, are related to such behavior. The third group of results is the most important, because it defines the quality of the fit achieved and therefore the reliability of the estimates made with the SPEI, since its mean, variance and percentage of droughts that it defines should be zero, the unit and 50%. As such indicators approximate the values quoted, the estimate will be better or more reliable.
As Table 1 shows, the most accurate estimates were those of durations of 12, 24 and 36 months, defining approximate percentages of 32.2, 11.5, 5.0 and 1.3 of light, moderate, severe and extreme droughts, respectively.
Figure 1a shows the historical evolution of SPEI with duration of 12 months, observing that in general there is alternation of wet and dry periods. The longest duration drought began towards the sequence 153 (September 1941) and ended in the 416 (August 1963). The date corresponding to a sequence is obtained by clearing from Equation 1 the value of NA in years, which is added to the initial year of the record. In this period the value of the most extreme SPEI occurs, with -2.742 in sequence 321 (October 1954).
Table 1 SPEI results with the monthly historical data of the climatological station Zacatecas, Mexico.
Table 2 Characteristic values of the historical climatic records and their hypothetic versions according to the probable climate change, in the climatological station Zacatecas, Mexico.
Table 3 SPEI results with the monthly altered records with combined effects (reduction of precipitation and increase of average temperature), in the climatological station Zacatecas, Mexico.
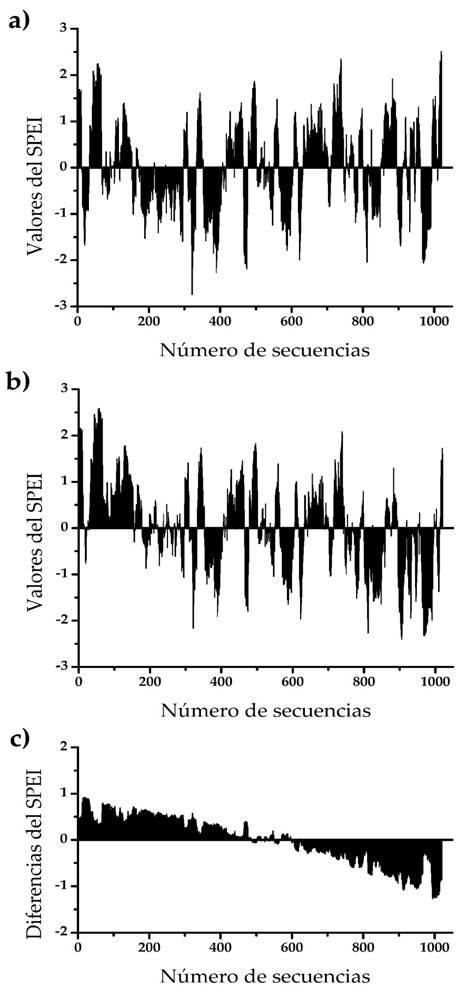
Figure 1 (a) SPEI evolution of 12 months duration in the climatological station Zacatecas, of the state of Zacatecas, Mexico; (b) SPEI evolution (k = 12 months) with reduction of 20% in the annual precipitation and increase of 4 °C in the average annual temperature and (c) Differences between the SPEI shown (b - c).
SPEI values with altered climate records
Based on equations 17 and 18, the historical records were modified to incorporate a progressive and linear decrease of 20% in annual precipitation and a progressive and linear increase of 4 °C in the average annual temperature. Table 2 shows various relevant values of the historical records and those of the altered or modified records according to possible climate change, as well as the annual values of the ETP estimated with the Thornthwaite method.
Similar to Table 1, in Table 3, the SPEI results for the altered record according to the third scenario are presented, i.e., considering the combined effect of both modifications. Due to space limitation the results of the SPEI with reduction of precipitation, and with increase in average temperature are not shown, but they are available with the author. Based on all the SPEI results, the duration of 24 months was defined as the ideal for the contrast between the values obtained with the historical record and the altered ones. This contrast is shown in Table 4.
Table 4 Number of events and percentages of each drought type obtained with SPEI of 24 months of duration in the historical records (Table 2) and their contrast with the altered ones (Table 3).
| Types of drought and SPEI | Table 2 | Reduction of precipitation | Reduction of precipitation | Combined effects |
| Light | 323 (32.0%) | 357 (35.4%) > | 356 (35.3%) > | 326 (32.3%) > |
| Moderate | 114 (11.3%) | 90 (8.9%) < | 88 (8.7%) < | 110 (10.9%) < |
| Severe | 58 (5.7%) | 53 (5.3%) < | 60 (5.9%) > | 45 (4.5%) < |
| Extreme | 13 (1.3%) | 21 (2.1%) > | 18 (1.8%) > | 18 (1.8%) > |
| SPEI minimum | -2.334 | -2.401 | -2.547 | -2.453 |
The results shown in Table 4 indicate that, in general, light and extreme droughts will increase as a result of probable climate change; in contrast, moderate and severe droughts will decrease. In these conclusions there is an anomaly in the severe droughts of the record with increase of temperature, which also increase. Regarding the extreme values of the SPEI, they are considered in agreement with the modifications imposed to the historical records. For the third scenario, the most critical, it is defined in Table 3 as more accurate results those of the 18-month duration, with the following percentages for the four types of droughts sought: 33.1, 9.9, 5.0 y 2.1.
Figure 1b shows the evolution of the SPEI of 12- month duration in the record that includes both effects of climate change; it is clear how droughts will increase in duration and severity towards the end of the record, significantly reducing the wet periods. Finally, Figure 1c shows the SPEI differences of Figure 1b minus 1a.
Conclusions
The results of the SPEI with the historical records of the climatological station Zacatecas (Table 1), located in the capital of the same name, in the state of Zacatecas, Mexico, define approximately 32.2%, 11.5%, 5.0% and 1.3% of light, moderate, severe and extreme droughts, respectively. These percentages and the following ones were obtained based on the drought durations of 12 to 30 months.
In the three scenarios of climate change, it is generally found that light and extreme droughts increase briefly and that moderate and severe droughts decrease, also scarcely in small number or percentage. They are defined globally for the third scenario (Table 3), the most critical, for combining precipitation reduction and average temperature increase, 32.7%, 10.5%, 4.8% and 2.0% for each type of drought.
The evolution graphs of SPEI, as those shown in Figure 1 for a 12-month drought duration, allow for accurate visualization and definition of drought periods, as well as their maximum or extreme point values; the before mentioned, both in the historical record and in the altered records by probable climatic change.
Taking into account, the consistency of the results of this study, the systematic application of SPEI in the quantification of historical and future droughts is recommended; the first based on the available historical records and the second ones, in their modified versions, that must be considered, according to the possible effects of climate change in each zone or region of the country.
In the climate change scenarios that are considered feasible to occur, SPEI results can help to put into perspective the impact on the water balance of a region. However, being uncertain how exactly droughts will evolve in the future, the SPEI results can only be considered as guidelines.
Referencias
Beguería, S., Vicente-Serrano, S. M., Reig, F., & Latorre, B. (2014). Standardized Precipitation Evapotranspiration Index (SPEI) revisited: parameter fitting, evapotranspiration models, tools, datasets and drought monitoring. International Journal of Climatology, 34(10), 3001-3023. [ Links ]
Campos-Aranda, D. F. (2005). Estimación de la evapotranspiración y análisis de la precipitación. Capítulos 3 y 4. En: Autor (ed.). Agroclimatología Cuantitativa de Cultivos (pp. 65-120). DF, México: Editorial Trillas. [ Links ]
Campos-Aranda, D. F. (2015). Contraste de los índices DPP, SPI y RDI para clasificación de sequías, en la estación climatológica Zacatecas, México. Tecnología y Ciencias del Agua, 6(1), 183-193. [ Links ]
Davis, P. J. (1972). Gamma Function and related functions. Chapter 6 (pp. 253-296). In: Abramowitz, M., & Stegun, I. (eds.). Handbook of Mathematical Functions. New York, USA: Dover Publications. [ Links ]
Fuchs, B. A., Svoboda, M. D., Wilhite, D. A., & Hayes, M. J. (2014). Drought indices for drought risk assessment in a changing climate. Chapter 12 (pp. 217-231). In: Eslamian, S. (ed.). Handbook of Engineering Hydrology. Modeling, Climate Change and Variability. Boca Raton, USA: CRC Press. [ Links ]
Haktanir, T. (1991). Statistical modelling of annual maximum flows in Turkish rivers. Hydrological Sciences Journal, 36(4), 367-389. [ Links ]
Hao, Z., & Singh, V. P. (2015). Drought characterization from a multivariate perspective: A review. Journal of Hydrology, 527, 668-678. [ Links ]
Ma, M., Ren, L., Yuan, F., Jiang, S., Liu, Y., Kong, H. & Gong, L. (2014). A new standardized Palmer drought index for hydro-meteorological use. Hydrological Processes, 28(23), 5645-5661. [ Links ]
Machiwal, D., & Jha, M. K. (2012). Hydrologic Time Series Analysis: Theory and Practice. Dordrecht, The Netherlands: Springer. [ Links ]
McKee, T. B., Doesken, N. J., & Kleist, J. (1993). The relationship of drought frequency and duration to times scales. 8th. Conference on Applied Climatology (pp. 179-184), Anaheim, California, United States of America. [ Links ]
Mavromatis, T. (2007). Drought index evaluation for assessing future wheat production in Greece. International Journal of Climatology, 27(7), 911-924. [ Links ]
Mishra, A. K., & Singh, V. P. (2010). A review of drought concepts. Journal of Hydrology, 391(1-2), 202-216. [ Links ]
Montero, M. J., Martínez, J., Castillo, N. I., & Espinoza, B. E. (2010). Escenarios climáticos en México proyectados para el siglo XXI: precipitación y temperatura máxima y mínima. En: Martínez, P. F., & Patiño, C. (eds.). Efectos del cambio climático en los recursos hídricos de México (pp. 39-63). Volumen III. Jiutepec, México: Secretaría de Medio Ambiente y Recursos Naturales-Instituto Mexicano de Tecnología del Agua. [ Links ]
Palmer, W. C. (1965). Meteorological Drought (Research Paper No. 45) (58 pp.). Washington, DC, USA: US Weather Bureau. [ Links ]
Pandey, R. P., Sharma, K. D., Mishra, S. K., Singh, R., & Agarwal, A. (2008). Drought characterization. Chapter 21 (pp. 761-792). In: Singh, V. P. (ed.). Hydrology and Hydraulics. Highlands Ranch, Colorado, USA: Water Resources Publications. [ Links ]
Secretaría de Agricultura y Recursos Hidráulicos, SARH. (1980). Boletín Climatológico No. 3. Región Hidrológica No. 37. El Salado. México, DF, México: Subsecretaría de Planeación, Secretaría de Agricultura y Recursos Hidráulicos, Secretaría de Agricultura y Recursos Hidráulicos. [ Links ]
Stagge, J. H., Tallaksen, L. M., Gudmundsson, L., Van Loon, A. F., & Stahl, K. (2015). Candidate distributions for climatological drought indices (SPI and SPEI). International Journal of Climatology, 35(13), 4027-4040. [ Links ]
Stedinger, J. R., Vogel, R. M., & Foufoula-Georgiou, E. (1993). Frequency Analysis of Extreme Events. Chapter 18. In: Maidment, D. R. (ed.). Handbook of Hydrology (18.1-18.66). New York, USA: McGraw-Hill, Inc. [ Links ]
Törnros, T., & Menzel, L. (2014). Addressing drought conditions under current and future climates in the Jordan River region. Hydrology and Earth System Sciences, 18(1), 305-318. [ Links ]
Tsakiris, G., & Vangelis, H. (2005). Establishing a drought index incorporating evapotranspiration. European Water, 9/10, 3-11. [ Links ]
Vicente-Serrano, S. M., Beguería, S., & López-Moreno, J. I. (2010). A multiscalar drought index sensitive to global warming: The Standardized Precipitation Evapotranspiration Index. Journal of Climate, 23(7), 1696-1718. [ Links ]
Wells, N., Goddard, S., & Hayes, M. J. (2004). A self-calibrating Palmer drought severity index. Journal of Climate, 17(12), 2335-2351. [ Links ]
World Meteorological Organization, WMO. (1971). Annexed III: Standard tests of significance to be recommended in routine analysis of climatic fluctuations. In: Climatic Change (Technical Note No. 79; WMO-No. 195). (pp. 58-71). Reprinted. Geneva, Switzerland: Secretariat of the World Meteorological Organization. [ Links ]
Wu, H., Svoboda, M. D., Hayes, M. J., Wilhite, D. A., & Wen, F. (2007). Appropriate application of the Standardized Precipitation Index in arid locations and dry seasons. International Journal of Climatology, 27(1), 65-79. [ Links ]
Zelen, M., & Severo, N. C. (1972). Probability Functions. Chapter 26. In: Abramowitz, M., & Stegun, I. (eds.). Handbook of Mathematical Functions (9th printing) (pp. 925-995). New York, USA: Dover Publications . [ Links ]
Received: March 30, 2016; Accepted: April 02, 2017











 texto en
texto en 


