Introducción
El centro y norte de México se encuentran dentro de la franja de alta presión de latitud norte, por lo que estas zonas son áridas y semiáridas, que coinciden en latitud con los grandes desiertos de África y Asia. En consecuencia, tales regiones no disponen de agua en cantidades suficientes y de forma histórica han sido afectadas por las sequías. En el siglo XX, México presentó cuatro grandes periodos de sequía: 1948-1954, 1960-1964, 1970-1978 y 1993-1996, así como una sequía severa en 1998, las cuales afectaron en particular a los estados del norte del país (Cenapred, 2007). De acuerdo con Escalante y Reyes (1998), el estado de Zacatecas, ubicado en el centro-norte de México, está entre los estados con más daños a la agricultura y la ganadería por las sequías ocurridas durante el periodo de 1988 a 1995.
Recientemente, en México se han registrado varias sequías de magnitud considerable entre los años 2000-2003, 2009 y 2011-2012. Entre los años 2000 y 2003, 18 de los 32 estados de México presentaron sequía; los estados del norte, incluyendo Zacatecas, fueron los más afectados. Las pérdidas económicas ascendieron a más de 1 800 millones de pesos (188 millones de dólares), cerca de un millón de hectáreas de cultivo fueron afectadas y se perdieron más de 13 mil cabezas de ganado (Cenapred, 2002; Cenapred, 2003; Cenapred, 2004). En 2009, México sufrió la segunda peor sequía en 60 años: los daños ascendieron a 3 081 millones de pesos (229 millones de dólares) y la superficie de cultivos y pastizales afectada fue de 384 540 hectáreas. Zacatecas estuvo entre los cinco estados con mayor superficie afectada (Semarnat, 2012). A finales de 2011 y hasta mediados de 2012, más de 60% de México sufrió la peor sequía en los últimos 70 años, clasificada según el Monitor de Sequía de América del Norte (NADM, por sus siglas en inglés) de intensidad severa a excepcional (Semarnat, 2012). Además, según el Departamento de Agricultura de los Estados Unidos de América (USDA, por sus siglas en inglés), esta sequía generó pérdidas económicas en el sector agrícola de más de 16 000 millones de pesos (1 300 millones de dólares) (Herron, 2013). El estado de Zacatecas fue de los más afectados por este desastre natural. Bajo tal contexto, es importante conocer el comportamiento puntual y regional de la sequía en el estado de Zacatecas para poder establecer medidas de mitigación.
Las sequías pueden tener repercusiones graves y duraderas en los sistemas naturales y humanos, que incluyen desastres humanitarios, pérdidas económicas y tensiones en los ecosistemas naturales (Touma, Ashfaq, Nayak, Kao, & Diffenbaugh, 2015). La sequía es impulsada por variaciones climáticas y por condiciones hidrológicas adversas (Li, Liang, Yu, & Acharya, 2014). Aunque la sequía es la consecuencia de una reducción natural en la cantidad de precipitación en un periodo de tiempo, su severidad se evalúa en términos de su duración, época de ocurrencia, extensión territorial afectada y, fundamentalmente, en los impactos que causa a las actividades humanas y agrícolas, así como al medio ambiente (Caparrini & Manzella, 2009). La sequía ha sido clasificada en cuatro categorías: meteorológica, hidrológica, agrícola y socioeconómica (Samaniego, Kumar, & Zink, 2013).
La complejidad para definir una sequía se debe a la dificultad de cuantificar su magnitud o severidad, pues por lo habitual ésta se identifica por sus efectos sobre diferentes sistemas (recursos hídricos, agricultura, ecología, pérdidas económicas, etc.); sin embargo, no existe una variable física que permita medir en específico la severidad de la sequía. La cuantificación de la sequía por lo general se realiza empleando índices de sequía (Asadi-Zarch, Sivakumar, & Sharma, 2015), los cuales se basan en información de precipitación, temperatura, evapotranspiración, caudales en ríos u otras variables hidrometeorológicas medibles, y que cuantifican el riesgo de sequía. En la actualidad existe una gran cantidad de índices para cuantificar las sequías; los más utilizados a nivel mundial son el Índice de Precipitación Estandarizado (SPI, por sus siglas en inglés) desarrollado por McKee, Doesken y Kleist (1993), que consiste en un enfoque probabilístico de la precipitación, y el Índice de Severidad de la Sequía de Palmer (PDSI, por sus siglas en inglés), desarrollado por Palmer (1965), que analiza el balance de agua en el suelo. Recientemente, la Organización Meteorológica Mundial (WMO, por sus siglas en inglés) presentó el SPI como el índice de sequía universal (Hayes, Svoboda, Wall, & Widhalm, 2011; WMO, 2012). La ventaja principal del SPI es que se puede calcular en diferentes escalas de tiempo (por lo habitual en 1, 3, 6, 9, 12, 24 y 48 meses) y representar las variaciones hidrológicas de los déficits de precipitación. Sin embargo, el SPI tiene una desventaja: sólo utiliza información de precipitación, sin tener en cuenta otras variables climatológicas que juegan un papel importante durante el desarrollo de un evento de sequía (Teuling et al., 2013). Recientemente, se han desarrollado índices que incorporan la evapotranspiración para evaluar la sequía. Por ejemplo, Tsakiris y Vangelis (2005), propusieron el Índice de Reconocimiento de Sequía (RDI, por sus siglas en inglés), que analiza el cociente entre la precipitación acumulada y la evapotranspiración potencial acumulada (ETP) desde un punto de vista probabilístico; por su parte, Vicente-Serrano, Beguería y López-Moreno (2010), desarrollaron el Índice de Precipitación-Evapotranspiración Estandarizado (SPEI, por sus siglas en inglés), que consiste en un balance hídrico climático mensual.
La complejidad del fenómeno de sequía hace que ningún índice de sequía se pueda aplicar en todas las regiones o sistemas naturales. Por lo tanto, para un análisis de sequía es conveniente considerar más de un índice, a fin de examinar la sensibilidad y precisión de cada uno de ellos, y explorar su comportamiento ante condiciones y finalidades específicas. La caracterización de un evento de sequía implica la identificación de la fecha de inicio y de finalización, su duración, magnitud (severidad) e intensidad (McKee et al., 1993; Kavalieratou, Karpouzos, & Babajimopoulos, 2012). Otras características de las sequías son la cobertura espacial (extensión superficial) y la frecuencia con que éstas ocurren (Kirono, Kent, Hennessy, & Mpelasoka, 2011).
Los objetivos de este trabajo fueron: (a) investigar las principales características de las sequías meteorológicas en el estado de Zacatecas durante el periodo de 1961 a 2012, utilizando los índices multiescalares de sequía SPI, RDI y SPEI; y (b) comparar el comportamiento temporal y espacial de los índices de sequía utilizados.
Materiales y métodos
Características del área de estudio
El estado de Zacatecas está ubicado entre las coordenadas 21° 01’ 00’’ y 25° 07’ 00’’ de latitud norte, y 100° 43’ 00’’ y 104° 22’ 00’’ de longitud oeste, y cuenta con una superficie de 75 284 km2. Los principales tipos de clima que presenta el estado son seco y semiseco (73%), y templado subhúmedo (17%). La temperatura media anual es de 17 °C, y las temperaturas máxima y mínima promedio anuales son de 30 °C (mayo) y 3 °C (enero), respectivamente. La precipitación media anual en Zacatecas es de 510 mm, con precipitaciones de 300 mm en el norte y de 860 mm en el sur; las lluvias se concentran en verano (75%), de junio a septiembre. El clima del estado de Zacatecas es una limitante para la agricultura, principal actividad económica, que destina alrededor de 1.74 millones de hectáreas, de las cuales 88% es de temporal (secano).
Información climatológica
Para identificar los eventos de sequía, así como para evaluar sus duraciones, magnitudes, e intensidades y frecuencias, en esta investigación se utilizaron las series de datos de precipitación y temperatura diaria de nueve estaciones climatológicas en el estado de Zacatecas (Figura 1), tomadas de la base de datos del CICLOM (Conagua, 2014), para el periodo del 1° de enero de 1961 al 31 de diciembre de 2012. Los descriptores geográficos (coordenadas y altitud) de las estaciones climatológicas y los valores medios anuales correspondientes a precipitación, P, y temperatura, T, se presentan en la Tabla 1.
Tabla 1 Estaciones climatológicas y su precipitación y temperatura media anual.
| Clave | Nombre | Latitud (N) | Longitud (O) | Altitud (msnm) | Periodo | Precipitación (mm) | Temperatura (ºC) |
|---|---|---|---|---|---|---|---|
| 32052 | San Rafael | 24º 35’ | 102º 06’ | 2 014 | 1961-2012 | 262.8 | 14.4 |
| 32028 | Juan Aldama | 24º 16’ | 103º 23’ | 1 999 | 1961-2012 | 433.0 | 18.0 |
| 32001 | Agua Nueva | 23º 47’ | 102º 09’ | 1 946 | 1961-2012 | 349.1 | 17.7 |
| 32054 | Sombrerete (DGE) | 23º 38’ | 103º 38’ | 2 300 | 1961-2012 | 551.4 | 16.4 |
| 32018 | El Sauz | 23º 16’ | 103º 06’ | 2 096 | 1961-2012 | 414.7 | 16.0 |
| 32003 | Calera | 22º 54’ | 102º 39’ | 2 097 | 1961-2012 | 426.5 | 15.6 |
| 32030 | La Florida | 22º 41’ | 103º 36’ | 1 870 | 1961-2012 | 590.3 | 16.4 |
| 32024 | Guadalupe Victoria | 22º 23’ | 101º 49’ | 2 132 | 1971-2012 | 374.1 | 16.4 |
| 32032 | La Villita | 21º 36’ | 103º 20’ | 1 786 | 1961-2012 | 782.3 | 20.4 |
Metodología
En esta investigación se emplearon tres de los índices de sequía más usados y conocidos a nivel internacional: el Índice de Precipitación Estandarizado, el Índice de Reconocimiento de Sequías y el Índice de Precipitación-Evapotranspiración Estandarizado. La caracterización de las sequías se llevó a cabo en seis etapas: 1) selección y control de calidad de la información climatológica; 2) selección de la escala de análisis; 3) cálculo de la evapotranspiración potencial (ETP); 4) cálculo de los índices SPI, RDI y SPEI en las escalas de tiempo de 3, 6 y 12 meses; 5) análisis de las características de las sequías; y 6) comparación de los índices de sequía meteorológica. En la Figura 2 se presenta de modo esquemático el desarrollo metodológico de la investigación.
Selección y control de calidad de la información climatológica
Una etapa fundamental en el análisis de series de tiempo hidroclimatológicas, como es el caso del análisis de sequías, es la selección y control de la calidad de la información. La selección de la información climatológica empleada se basó en particular en cuatro criterios: (1) que la estación climatológica estuviera activa para poder evaluar las sequías de los últimos años; (2) que la longitud de los registros de precipitación y temperatura de cada estación climatológica fuera de al menos 40 años; (3) que el porcentaje de datos faltantes fuera menor o igual al 15%, para no perder representatividad en los datos; y (4) que las estaciones estuvieran distribuidas en toda la zona de estudio, a fin de tener una buena representación espacial de la sequía.
Para el análisis de la sequía se llevaron a cabo controles de calidad preliminares de las series de datos de precipitación y temperatura, revisando la homogeneidad de las series de información climatológica y completando los datos faltantes. Para revisar la homogeneidad de los datos de precipitación y temperatura se aplicaron pruebas estadísticas paramétricas y no paramétricas a las series anuales. Las pruebas seleccionadas fueron la t de Student, la prueba de Cramer (Mirza, 1997), y las Pruebas de Homogeneidad Normal Estándar (SNHT, por sus siglas en inglés) y de Buishand (Hänsel, Medeiros, Matschullat, Petta, & De Mendonça-Silva, 2016).
Para seleccionar el método de complementación de datos faltantes se probaron varios métodos: interpolación polinomial, promedio aritmético, inverso de la distancia y relación normal (Tabios III & Salas, 1985; Dingman, 2002); el método que presentó mejores resultados fue el de la relación normal (ecuación (1)):
donde
Selección de las escalas de análisis de la sequía (k)
Para investigar las características de la sequía, la escala de tiempo
En esta investigación fueron seleccionadas las escalas
Cálculo de la evapotranspiración potencial (ETP)
Para el cálculo de los índices RDI y SPEI, la evapotranspiración potencial fue estimada mediante el método de Thornthwaite (1948), como lo proponen Tsakiris y Vangelis (2005), y Vicente-Serrano et al. (2010). Este método es uno de los más sencillos para calcular la ETP (ecuación (2)), ya que sólo requiere de datos de temperatura media mensual y la latitud del lugar donde se desea estimar la ETP:
donde
donde
y
en la cual,
donde
El Índice de Precipitación Estandarizado (SPI)
El SPI considera la precipitación como variable única de análisis y estima si en
una región, en un determinado periodo, hay déficit o exceso de precipitación
respecto a las condiciones normales (Hayes,
Svoboda, Wilhite, & Vanyarkho, 1999). El cálculo del SPI se basa
en registros de precipitación de largo plazo; Guttman (1994) señala que se necesitan de preferencia registros de
50 a 60 años o más, aunque otros investigadores (Wu, Hayes, Wilhite, & Svoboda, 2005; Li et al., 2014) recomiendan tener al
menos 30 años. El SPI se calcula ajustando una función de distribución de
probabilidad (fdp) apropiada, generalmente la función de distribución Gamma, a
los datos de precipitación mensual acumulada, para cada escala de tiempo
donde
donde
donde
Integrando la función de densidad Gamma (ecuación (9)) con respecto a
Considerando
Dado que la función Gamma no está definida para
donde
Si
Finalmente, para definir el valor del SPI, la distribución de probabilidad
acumulada
donde
Un evento de sequía ocurre cuando a cualquier escala de tiempo, el SPI es continuamente negativo y alcanza un valor de -1.0 o menor, y termina cuando el SPI llega a ser positivo (McKee et al., 1993; Vrochidou y Tsanis, 2012). Los valores del SPI se pueden comparar con facilidad y de forma simultánea en los ámbitos espacial y temporal (Lopez-Bustins, Pascual, Pla, & Retana, 2013). Con base en el rango de valores del SPI, los eventos de sequía se clasifican de ligeros a extremos (Tabla 2).
Tabla 2 Clasificación del SPI (McKee et al., 1993).
| Valor SPI | Clasificación |
|---|---|
| ≥ 2.00 | Extremadamente húmedo |
| 1.50 a 1.99 | Severamente húmedo |
| 1.00 a 1.49 | Moderadamente húmedo |
| 0 a 0.99 | Ligeramente húmedo (cercano a lo normal) |
| 0 a -0.99 | Sequía ligera (cercano a lo normal) |
| -1.00 a -1.49 | Sequía moderada |
| -1.50 a -1.99 | Sequía severa |
| ≤ -2.00 | Sequía extrema |
El Índice de Reconocimiento de Sequías (RDI)
El RDI se puede calcular en diferentes escalas de tiempo y su interpretación es
similar a la del SPI (Tabla 2) (Vicente-Serrano, Van der Schrier, Beguería,
Azorin-Molina, & López-Moreno, 2015; Xu et al., 2015). Entre las principales
limitaciones teóricas de este índice de sequía se destaca que no es válido
cuando el valor de la ETP es igual a 0, lo cual es muy común en regiones frías
en invierno (Vicente-Serrano et
al., 2015). El RDI se expresa en tres formas: el valor
inicial (
donde
Las formas normalizada y estandarizada del RDI son (Tsakiris, Pangalou, & Vangelis, 2007):
donde
De acuerdo con diferentes investigaciones con datos de distintos lugares y
diferentes escalas de tiempo de análisis, se observó que en casi todos los
casos, los valores de
Según Tigkas (2008) y Asadi-Zarch et al. (2011)
se ha probado que el cálculo de RDIst podría realizarse mejor ajustando la
distribución Gamma a la distribución de frecuencias de
En este estudio, el RDI se obtuvo ajustando la distribución Gamma a los valores
El Índice de Precipitación-Evapotranspiración Estandarizado (SPEI)
La principal limitación del SPI es que se basa sólo en la precipitación e ignora otras variables que afectan la demanda de agua atmosférica, como temperatura, velocidad del viento, radiación solar y déficit de presión de vapor (McEvoy, Huntington, Abatzoglou, & Edwards, 2012). Para superar esta limitación, Vicente-Serrano et al. (2010) desarrollaron el SPEI, el cual combina la sensibilidad del PDSI con los cambios en la demanda de la evaporación causados por fluctuaciones y tendencias de la temperatura, con la sencillez de cálculo y la naturaleza multiescalar del SPI (Vicente-Serrano et al., 2010; Banimahd & Khalili, 2013; Li et al., 2014).
El SPEI se basa en un balance de agua climático mensual (precipitación menos evapotranspiración potencial, llamada serie D) que se calcula en diferentes escalas de tiempo y matemáticamente es similar al SPI, pero incluye el papel de la evapotranspiración potencial (López-Moreno et al., 2013). Su cálculo sigue un enfoque similar al seguido para el cálculo del SPI, pero utilizando una distribución de probabilidad Log-logística de tres parámetros en lugar de la distribución Gamma de dos parámetros (Figura 2). La clasificación de sequía del SPI puede ser usada también para evaluar el SPEI (Tabla 2).
Para el cálculo del SPEI, primero se calcula la diferencia entre la precipitación
y la evapotranspiración potencial del mes
donde
Para el cálculo del SPEI es necesario utilizar una distribución de probabilidad
de tres parámetros, dado que en una de dos parámetros, la variable
donde
Los parámetros de la distribución Log-logística pueden obtenerse por diferente métodos, de los cuales, el método de momentos L es el más robusto y de fácil aplicación (Ahmad, Sinclair, & Werritti, 1988; Singh, Guo, & Yu, 1993):
donde
donde
La distribución de probabilidad de las series
Finalmente, para obtener los valores del SPEI, los valores de
Comparación de los índices de sequía
Los índices SPI, RDI y SPEI siguen metodologías similares y sus valores tienen el
mismo significado estadístico, por lo tanto, son comparables. Para realizar la
comparación entre los índices de sequía se utilizaron los coeficientes de
correlación de Pearson (
Resultados y discusión
En esta investigación se definió un evento de sequía como aquel en el que los valores del SPI, RDI o SPEI toman valores del índice iguales o menores a -1.0. Se determinó el número de eventos de sequía, así como la duración y magnitud de cada evento para las escalas de 3, 6 y 12 meses, para cada una de las nueve estaciones analizadas.
Un análisis general de los índices de sequía analizados muestra que tanto local como regionalmente estos índices siguen el mismo patrón temporal para el periodo de 1961-2012. De acuerdo con el SPI, el RDI y el SPEI, los periodos húmedos más importantes fueron de 1965-1968, 1990-1992 y 2003-2005, y los principales eventos de sequía se produjeron en 1969-1970, 1982-1983, 1998-2000 y 2010-2012.
Los tres índices analizados mostraron resultados consistentes en la detección de los grandes eventos de sequía respecto a su magnitud y duración (Tabla 3). Las series del SPI, RDI y SPEI tuvieron pocas diferencias entre sí, independientemente de la escala de tiempo de análisis. Estos resultados muestran que en condiciones climáticas donde existe baja variabilidad interanual de la temperatura, los índices de sequía analizados responden principalmente a la variabilidad de la precipitación.
Los resultados de los índices SPI y RDI son similares en las escalas de 3 y 6 meses (SPI-3 y RDI-3; y SPI-6 y RDI-6). Con el SPI-3 y el RDI-3 la mayoría de los periodos de sequía se detectó en los meses de enero a mayo; con el SPEI-3 se detectó de abril a julio. Respecto al SPI-6 y RDI-6, la mayoría de los periodos secos ocurrió en los meses de marzo a junio; con el SPEI-6 se presentó de mayo a septiembre. Se observa que, para estas escalas, el SPEI detecta la sequía varios meses después que el SPI y el RDI debido a la relación que existe entre precipitación y temperatura en los primeros meses del año. En la escala de 12 meses, los resultados de los tres índices son similares, aunque en los periodos importantes en cuanto a duración, magnitud e intensidad presentan mayor semejanza el SPI-12 y el RDI-12. Según el SPI-12, el RDI-12 y el SPEI-12 en 1962, 1969, 1979, 1982, 1998, 1999, 2000, 2011 y 2012 hubo importantes periodos de sequía. Años que en su mayoría fueron detectados con sequía por Campos-Aranda (2014) en la estación climatológica Fresnillo en el centro de Zacatecas, con el Índice del Déficit Probabilístico de Precipitación, el SPI y el RDI. Campos-Aranda (2016) también reportó sequías en una escala anual en gran parte de Zacatecas con el índice de aridez en estos mismos años. El periodo de sequía más importante en cuanto a intensidad se presentó entre 2011 y 2012.
La evolución de las series SPI, RDI y SPEI en la escala de tres meses (corto plazo) presentó una frecuencia temporal alta de los periodos de sequía y de humedad. Conforme la escala de tiempo se incrementa a 6 y 12 meses, los periodos secos y húmedos mostraron una frecuencia temporal menor y una mayor duración (Figura 3). Se definen con mayor claridad las temporadas secas y húmedas, sobre todo en la escala de 12 meses.
Tabla 3 Valores máximos de las características de las sequías para todas las estaciones y escalas de tiempo.
| Índice | Estación | Duración | Severidad (magnitud) | Intensidad | |||
|---|---|---|---|---|---|---|---|
| Valor | Periodo | Valor | Periodo | Valor | Periodo | ||
| 32052 | 6 | 12/2010 - 05/2011 | -8.426 | 12/2010 - 05/2011 | -1.483 | 04/1962 - 04/1962 | |
| 32028 | 7 | 12/1988 - 06/1989 | -9.005 | 12/1988 - 06/1989 | -1.361 | 04/1964 - 04/1964 | |
| SPI-3 | 32018 | 6 | 12/2010 - 05/2011 | -9.696 | 12/2010 - 05/2011 | -1.713 | 01/1972 - 02/1972 |
| 32024 | 6 | 12/2000 - 05/2001 | -9.396 | 12/2000 - 05/2001 | -1.574 | 04/1973 - 04/1973 | |
| 32032 | 6 | 12/2002 - 05/2003 | -8.936 | 12/2010 - 04/2011 | -1.787 | 12/2010 - 04/2011 | |
| 32052 | 7 | 12/2010 - 06/2011 | -9.711 | 12/2010 - 06/2011 | -1.483 | 02/1966 - 02/1966 | |
| 32028 | 7 | 12/1988 - 06/1989 | -9.109 | 12/1988 - 06/1989 | -1.361 | 04/1964 - 04/1964 | |
| RDI-3 | 32018 | 6 | 12/2010 - 05/2011 | -9.877 | 12/2010 - 05/2011 | -1.713 | 01/1972 - 02/1972 |
| 32024 | 6 | 12/2000 - 05/2001 | -9.414 | 12/2000 - 05/2001 | -1.574 | 04/1961 - 05/1961 | |
| 32032 | 6 | 12/2010 - 05/2011 | -10.102 | 12/2010 - 05/2011 | -1.787 | 05/1970 - 05/1970 | |
| 32052 | 6 | 05/1974 - 10/1974 | -9.775 | 05/1974 - 10/1974 | -1.900 | 06/1965 - 06/1965 | |
| 32028 | 5 | 04/1982 - 08/1982 | -8.923 | 05/1980 - 08/1980 | -2.231 | 05/1980 - 08/1980 | |
| SPEI-3 | 32018 | 5 | 05/1962 - 09/1962 | -7.463 | 05/1962 - 09/1962 | -2.048 | 05/1990 - 06/1990 |
| 32024 | 4 | 04/1989 - 07/1989 | -7.247 | 04/1989 - 07/1989 | -1.969 | 05/1998 - 06/1998 | |
| 32032 | 4 | 04/2011 - 07/2011 | -9.134 | 04/2011 - 07/2011 | -2.320 | 05/2010 - 06/2010 | |
| 32052 | 10 | 12/1984 - 09/1985 | -14.918 | 12/1984 - 09/1985 | -2.416 | 05/1980 - 05/1980 | |
| 32028 | 6 | 02/1989 - 07/1989 | -10.971 | 02/1989 - 07/1989 | -2.173 | 04/1979 - 05/1979 | |
| SPI-6 | 32018 | 5 | 03/2011 - 07/2011 | -10.564 | 03/2011 - 07/2011 | -2.113 | 03/2011 - 07/2011 |
| 32024 | 6 | 01/2001 - 06/2001 | -12.945 | 01/2001 - 06/2001 | -2.189 | 02/1990 - 05/1990 | |
| 32032 | 4 | 03/2011 - 06/2011 | -8.633 | 03/2011 - 06/2011 | -2.525 | 04/1991 - 05/1991 | |
| 32052 | 15 | 12/1984 - 02/1986 | -20.798 | 12/1984 - 02/1986 | -2.437 | 05/1980 - 05/1980 | |
| 32028 | 5 | 03/1989 - 07/1989 | -10.325 | 03/1989 - 07/1989 | -2.094 | 04/1991 - 06/1991 | |
| RDI-6 | 32018 | 6 | 03/2011 - 08/2011 | -12.613 | 03/2011 - 08/2011 | -2.166 | 02/1976 - 06/1976 |
| 32024 | 6 | 01/2001 - 06/2001 | -13.096 | 01/2001 - 06/2001 | -2.243 | 04/1981 - 05/1981 | |
| 32032 | 4 | 03/2011 - 06/2011 | -9.290 | 03/2011 - 06/2011 | -2.622 | 04/1991 - 05/1991 | |
| 32052 | 6 | 06/1974 - 11/1974 | -10.257 | 06/1974 - 11/1974 | -1.877 | 07/1989 - 11/1989 | |
| 32028 | 6 | 06/1980 - 11/1980 | -12.848 | 06/1980 - 11/1980 | -2.141 | 06/1980 - 11/1980 | |
| SPEI-6 | 32018 | 7 | 05/2011 - 11/2011 | -12.414 | 05/2011 - 11/2011 | -1.881 | 07/1962 - 11/1962 |
| 32024 | 7 | 04/1989 - 10/1989 | -12.949 | 04/1989 - 10/1989 | -1.850 | 04/1989 - 10/1989 | |
| 32032 | 9 | 03/2011 - 11/2011 | -16.395 | 03/2011 - 11/2011 | -1.822 | 03/2011 - 11/2011 | |
| 32052 | 40 | 06/1985 - 09/1988 | -65.884 | 06/1985 - 09/1988 | -1.837 | 11/1975 - 05/1976 | |
| 32028 | 18 | 07/2011 - 12/2012 | -30.437 | 07/2011 - 12/2012 | -2.074 | 06/1978 - 06/1978 | |
| SPI-12 | 32018 | 18 | 02/2011 - 07/2012 | -38.158 | 02/2011 - 07/2012 | -2.120 | 02/2011 - 07/2012 |
| 32024 | 20 | 08/1989 - 03/1991 | -35.080 | 08/1989 - 03/1991 | -1.754 | 08/1989 - 03/1991 | |
| 32032 | 23 | 02/2011 - 12/2012 | -44.154 | 02/2011 - 12/2012 | -1.920 | 02/2011 - 12/2012 | |
| 32052 | 40 | 06/1985 - 09/1988 | -61.101 | 06/1985 - 09/1988 | -1.832 | 11/1975 - 05/1976 | |
| 32028 | 14 | 07/2011 - 08/2012 | -24.325 | 07/2011 - 08/2012 | -1.835 | 06/1982 - 04/1983 | |
| RDI-12 | 32018 | 18 | 02/2011 - 07/2012 | -36.955 | 02/2011 - 07/2012 | -2.053 | 02/2011 - 07/2012 |
| 32024 | 20 | 08/1989 - 03/1991 | -35.433 | 08/1989 - 03/1991 | -1.772 | 08/1989 - 03/1991 | |
| 32032 | 23 | 02/2011 - 12/2012 | -52.654 | 02/2011 - 12/2012 | -2.289 | 02/2011 - 12/2012 | |
| 32052 | 25 | 12/1961 - 12/1963 | -40.618 | 12/1961 - 12/1963 | -1.625 | 12/1961 - 12/1963 | |
| 32028 | 12 | 06/1980 - 05/1981 | -22.007 | 06/1980 - 05/1981 | -1.935 | 06/1982 - 04/1983 | |
| SPEI-12 | 32018 | 18 | 02/2011 - 07/2012 | -30.817 | 02/2011 - 07/2012 | -1.814 | 08/1962 - 06/1963 |
| 32024 | 24 | 06/1989 - 05/1991 | -38.493 | 06/1989 - 05/1991 | -1.629 | 12/1971 - 11/1972 | |
| 32032 | 26 | 11/2010 - 12/2012 | -50.699 | 11/2010 - 12/2012 | -1.950 | 11/2010 - 12/2012 | |

Figura 3 Evolución temporal de la sequía en las escalas de 3, 6 y 12 meses en la estación El Sauz (32018).
Características medias de las sequías
En la Tabla 4 se presenta un resumen del número de eventos de sequía y su duración media, para periodos de sequía a corto, mediano y largo plazos, determinados con los tres índices de sequía evaluados. El número medio de episodios de sequía disminuyó con el aumento de las escalas de tiempo.
El número de eventos de sequía promedio en una escala de tiempo a corto plazo varió entre 36 y 48 para el SPI-3, de 41 a 49 para el RDI-3 y de 38 a 52 para el SPEI-3. La duración media de los eventos de sequía osciló de 2.3 a 2.9, de 2.2 a 2.7 y de 2.0 a 3.2 meses para el SPI-3, el RDI-3 y el SPEI-3, respectivamente. En 70% de las estaciones climatológicas el evento de sequía de mayor magnitud alcanzó la categoría de sequía severa, con el SPI-3 y el RDI-3, mientras que con el SPEI-3, 90% de las estaciones climatológicas alcanzó la categoría de sequía extrema. La duración máxima de los periodos de sequía registrados con el SPI-3 y el RDI-3 varió de 5 a 8 meses, mientras que para el SPEI-3 dicha duración fue de 4 a 7 meses.
En las dos últimas décadas se presentaron los eventos de sequía más intensos en la escala de tres meses. Según el SPI-3 y el RDI-3, estos eventos fueron de febrero a mayo de 1999, y de enero a mayo de 2011, y de acuerdo con el SPEI-3 éstos fueron de mayo a julio de 2011 y de mayo a junio de 1998.
Para la escala de seis meses, los eventos de sequía detectados por los tres índices presentan resultados relativamente similares. Los eventos de sequía promedio variaron de 28 a 41, de 26 a 39 y de 27 a 39 para el SPI-6, el RDI-6 y el SPEI-6, respectivamente. La duración media de tales eventos va desde 2.6 a 3.1 meses para el SPI-6, de 2.7 a 3.2 meses para el RDI-6 y de 2.9 a 4.1 meses para el SPEI-6. Los eventos de mayor intensidad alcanzaron la categoría de sequía extrema con el SPI-6 y el RDI-6 en todas las estaciones; con el SPEI-6 sólo 20% alcanzó esta categoría, las demás estaciones presentaron sequía severa. De acuerdo con el SPEI-6, las duraciones máximas de los periodos secos fueron muy similares entre estaciones, variando de 6 a 9 meses, mientras que de acuerdo con el SPI-6 y el RDI-6 presentaron mayor variación, de 4 a 15 meses.
Con base en el SPI-6, el RDI-6 y el SPEI-6, la región noreste de Zacatecas presentó sequías importantes en cuanto a magnitud e intensidad en las décadas de 1970 y 1980. Para las décadas de 1990 y 2000, las sequías importantes se presentaron en el centro y sur del estado.
Tabla 4 Número de eventos y (duración media) de los eventos de sequía determinados por el SPI, el RDI y el SPEI para el periodo 1961-2012. * El registro de esta estación es de 1971-2012.
| Estación | SPI-3 | RDI-3 | SPEI-3 | SPI-6 | RDI-6 | SPEI-6 | SPI-12 | RDI-12 | SPEI-12 |
|---|---|---|---|---|---|---|---|---|---|
| 32052 | 43 (2.4) | 44 (2.2) | 38 (3.2) | 28 (3.1) | 30 (3.0) | 27 (4.1) | 16 (6.8) | 14 (8.1) | 19 (6.1) |
| 32028 | 36 (2.8) | 41 (2.7) | 47 (2.3) | 41 (2.6) | 39 (2.7) | 34 (2.9) | 21 (5.1) | 16 (5.8) | 19 (5.1) |
| 32001 | 37 (2.9) | 42 (2.5) | 45 (2.6) | 32 (3.0) | 26 (3.2) | 34 (3.2) | 10 (6.2) | 11 (5.6) | 19 (4.6) |
| 32054 | 42 (2.3) | 46 (2.3) | 47 (2.1) | 38 (3.1) | 34 (3.0) | 36 (3.1) | 13 (8.9) | 12 (9.4) | 13 (9.1) |
| 32018 | 48 (2.3) | 49 (2.4) | 51 (2.2) | 37 (2.9) | 36 (2.8) | 35 (3.0) | 18 (5.7) | 19 (5.1) | 18 (5.8) |
| 32003 | 41 (2.3) | 41 (2.3) | 48 (2.0) | 39 (2.8) | 33 (3.0) | 33 (3.3) | 19 (5.2) | 20 (5.0) | 21 (5.4) |
| 32024* | 31 (2.8) | 34 (2.5) | 40 (2.1) | 26 (3.1) | 26 (3.0) | 28 (3.3) | 16 (5.4) | 19 (4.8) | 18 (5.3) |
| 32032 | 47 (2.5) | 46 (2.6) | 44 (2.1) | 38 (2.8) | 37 (2.9) | 39 (2.9) | 18 (5.7) | 15 (6.7) | 13 (8.2) |
| 32030 | 44 (2.5) | 47 (2.4) | 52 (2.0) | 34 (3.1) | 31 (3.1) | 37 (3.1) | 19 (4.8) | 21 (4.2) | 18 (5.7) |
En la escala de seis meses, el RDI-6 detectó el periodo de sequía de mayor duración (15 meses), el cual ocurrió en la región norte de Zacatecas (estación 32052). El periodo de sequía más largo detectado por el SPI-6 fue en la estación 32001 (norte de Zacatecas), también detectado por el RDI-6, el cual duró 13 meses, de junio de 1987 a junio de 1988. El SPEI-6 detectó sequía para este mismo periodo y estación, pero en dos subperiodos, uno de seis meses (de julio a diciembre de 1987) y otro de tres (de mayo a julio de 1988). El periodo de sequía de mayor duración detectado con el SPEI-6 fue de nueve meses en las estaciones 32032 y 32054, de marzo a noviembre de 2011, sur y centro-oeste de Zacatecas, respectivamente. En este mismo periodo, el SPI-6 y el RDI-6 detectaron un periodo de sequía de sólo cuatro meses, de marzo a junio de 2011.
Respecto a la escala de tiempo de 12 meses (mediano y largo plazo), el número de eventos de sequía promedio es similar para los tres índices, variando de 10 a 21 para el SPI-12, de 11 a 21 para el RDI-12 y de 13 a 21 para el SPEI-12. La duración media de los eventos de sequía oscila de 4.8 a 8.9 para el SPI-12, de 4.2 a 9.4 para el RDI-12 y de 4.6 a 9.1 meses para el SPEI-12. En esta escala, los eventos de mayor intensidad alcanzaron la categoría de sequía extrema en 70% de las estaciones con el SPI-12 y el RDI-12, y 30% de sequía severa, mientras que con el SPEI-12, sólo el 10% de las estaciones presentó sequía extrema, el 90% restante presentó sequía severa. Las duraciones máximas de los periodos secos mediante el SPI-12 y el RDI-12 fueron similares, variando de 16 a 40 y de 14 a 40 meses, respectivamente; estas duraciones fueron menores para el SPEI-12, variando de 12 a 27 meses.
Durante el periodo de 52 años de registros climatológicos analizados en el estado de Zacatecas, las intensidades máximas de sequía en la escala de tiempo anual fueron detectadas por el SPI, lo cual coincide con los resultados obtenidos por Campos-Aranda (2014, 2015) al analizar las sequías con el SPI y el RDI en el centro de Zacatecas; en las escalas de 3 y 6 meses, las intensidades máximas de sequía fueron detectadas por el SPEI y el RDI, respectivamente.
Las sequías de mayor intensidad para las tres escalas de tiempo se presentaron entre 1998 y 2011. El RDI y el SPEI también identificaron sequías extremas en 1974, 1979, 1982 y 1989. En la Figura 4 se muestra la distribución espacial del SPI, el RDI y el SPEI en el mes de mayor sequía en las tres escalas de tiempo analizadas. En la escala de tres meses, el SPI-3 y el RDI-3 identificaron el mes de abril de 2011 como el de mayor intensidad de sequía; dichos índices tienen un comportamiento espacial prácticamente igual (Figura 4a y Figura 4b). La mayor parte de Zacatecas (82%) presentó sequía severa y sólo el 8% sequía extrema. En junio de 2011 se presentó la sequía de mayor intensidad con el SPEI-3, con sequía extrema en 59% del estado, principalmente en la parte centro (Figura 4c). En la escala de seis meses, abril de 2011 también fue el mes de mayor intensidad de sequía con el SPI y RDI, el cual presentó sequía extrema en prácticamente todo el territorio de Zacatecas (Figura 4d y Figura 4e). Julio de 2011 fue el mes de mayor sequía identificado por el SPEI-6; la mayor parte del territorio presentó sequía extrema (49%) y severa (39%). La sequía extrema ocurrió sobre todo en el centro y noreste de Zacatecas. En la escala de 12 meses, septiembre de 2011 fue el mes de mayor intensidad de sequía identificado por los tres índices. El SPI-12 y el RDI-12 tuvieron un comportamiento espacial semejante: identifican alrededor de 55% de Zacatecas con sequía extrema (Figura 4g y Figura 4h), principalmente sur y oeste del estado. El SPEI-12 identificó sequía extrema en 33% de Zacatecas, en las mismas regiones que el SPI-12 y el RDI-12, pero con una extensión menor.
Frecuencia de las sequías
La frecuencia de las sequías se analizó con base en las diferentes clases de sequía (Tabla 2) relacionadas con los valores de los índices de sequía (SPI, RDI y SPEI). En la escala de tres meses, para los índices de sequía analizados, el tiempo promedio (porcentaje de frecuencia promedio) de periodos secos y húmedos fue de 17.1 y 16.9%, respectivamente. El 66.0% del tiempo presentó condiciones normales de precipitación. El SPI-3 y el RDI-3 presentaron mayor frecuencia de sequías moderadas (12.5 y 12.2%, respectivamente) que el SPEI-3, mientras que la frecuencia de sequías severas fue menor para el SPI-3 y el RDI-3 (4.1 y 4.8%, respectivamente) que para el SPEI-3. De los tres índices, el SPI-3 y el RDI-3 presentaron el menor número de sequías extremas. En la Figura 5a se observa el porcentaje de frecuencia de periodos secos y húmedos para el SPI-3, el RDI-3 y el SPEI-3. Con el SPI-3 y el RDI-3 sólo la región centro-oeste de estudio (estación 32054) presentó sequías extremas (14 y 15 eventos, respectivamente), mientras que con el SPEI-3 todas las estaciones presentaron eventos de sequía extrema, variando de 3 a 16 eventos para las estaciones 32052 y 32032, norte y sur de Zacatecas, respectivamente.
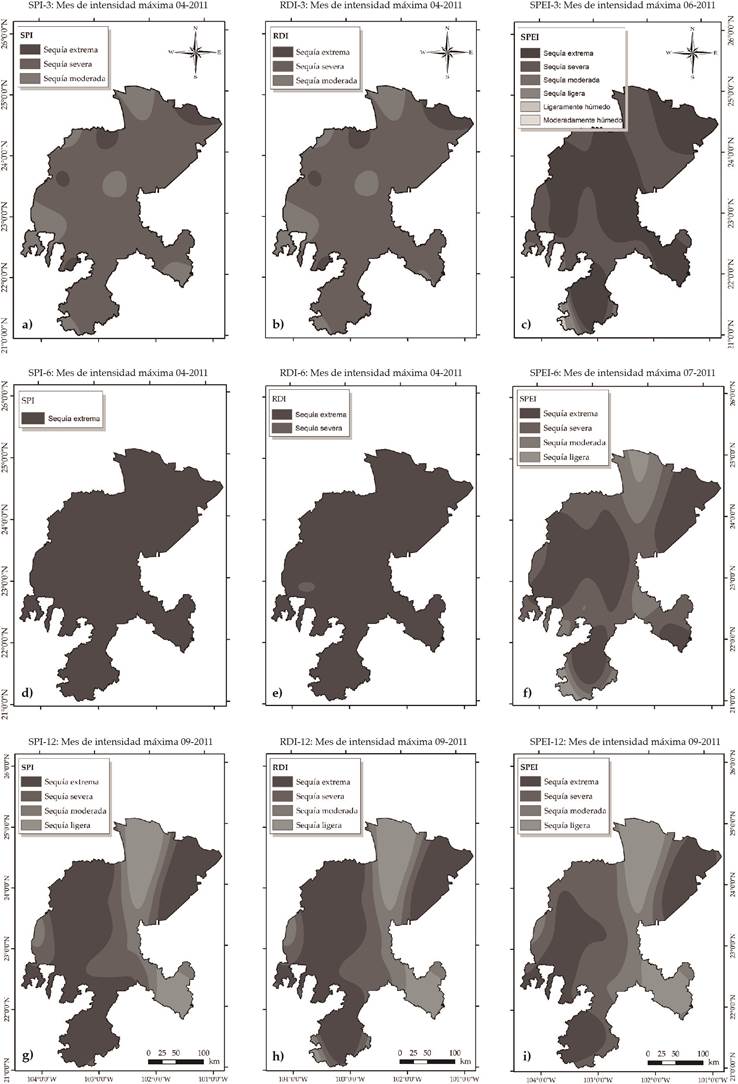
Figura 4 Distribución espacial de los índices SPI, RDI y SPEI en el mes de sequía más intensa para las escalas de 3, 6 y 12 meses.

Figura 5 Distribución de frecuencia de los valores de los índices SPI, RDI y SPEI: a) escala de tres meses; b) escala de seis meses; y c) escala de 12 meses, para el periodo de 1961-2012.
En la escala de seis meses, según los tres índices multiescalares, en promedio 67.4% del tiempo hubo condiciones normales de precipitación. La frecuencia de los eventos secos fue de 16.7%, y de los eventos húmedos de 15.9%. El SPEI-6 presentó mayor frecuencia de sequías moderadas (11.0%) que el SPI-6 y el RDI-6 (8.7 y 7.7%, respectivamente). Lo mismo ocurrió con las sequías severas (Figura 5b). Sin embargo, el SPI-6 y el RDI-6 presentaron mayor frecuencia de sequías extremas que el SPEI-6, 3.4 y 3.8%, respectivamente. Con el SPI-6 y el RDI-6 se detectaron 26 y 29 eventos de sequía extrema, los cuales ocurrieron en el centro de Zacatecas (estaciones 32018 y 32030, respectivamente), mientras que con el SPEI-6, el número máximo de eventos de sequía extrema fue de 15, aconteciendo en la región norte (estación 32001). Por último, en la escala de 12 meses, el porcentaje de frecuencia promedio, de eventos normales, húmedos y secos fue de 66.6, 16.9 y 16.5%, respectivamente. La frecuencia de eventos de sequía para el SPI-12, el RDI-12 y el SPEI-12 fueron 16.3, 15.8 y 17.4%, respectivamente. El comportamiento y los valores de la frecuencia de las diferentes clases de sequía para el SPI-12, el RDI-12 y el SPEI-12 son similares a los que presentan el SPI-6, el RDI-6 y el SPEI-6. Es decir, el SPEI-12 presenta mayor frecuencia de ocurrencia de sequías moderadas y severas que el SPI-12 y el RDI-12, y para sequías extremas sucede lo contrario, como se observa en la Figura 5c. Con el SPI-12 y el RDI-12 se detectaron 23 y 22 eventos de sequía extrema en la estación 32032 (sur de Zacatecas), mientras que con el SPEI-12, el número máximo de eventos de sequía extrema fue de 17 en la estación 32001 (norte de Zacatecas).
Correlación entre los índices de sequía
Considerando las tres escalas de tiempo y las nueve estaciones analizadas, los
índices SPI vs. RDI son los índices que tienen correlación más
alta, y sus coeficientes de correlación
En la escala de tres meses, los coeficientes de correlación r entre SPI-3 vs. RDI-3 varían de 0.920 a 0.969, mientras que entre SPI-3 vs. SPEI-3 y RDI-3 vs. SPEI-3 varían de 0.336 a 0.804 y de 0.583 a 0.867, respectivamente. En general, las correlaciones para la escala de seis meses fueron ligeramente más altas que para la escala de tres meses, variando de 0.943 a 0.964 para SPI-6 vs. RDI-6, de 0.410 a 0.834 para SPI-6 vs. SPEI-6, y de 0.643 a 0.906 para RDI-6 vs. SPEI-6. En la escala de 12 meses, los coeficientes de correlación varían de 0.952 a 0.996 para SPI-12 vs. RDI-12, de 0.926 a 0.982 para SPI-12 vs. SPEI-12, y de 0.952 a 0.993 para RDI-12 vs. SPEI-12. Se observó que para las escalas y estaciones analizadas, a menor escala, menor correlación entre los índices (Tabla 5). En las escalas de 3 y 6 meses, las correlaciones más bajas se presentaron al norte del estado de Zacatecas (estación 32052) y las más altas al sur (estación 32032).
Los valores de los coeficientes de correlación de Spearman (Tabla 5) presentaron valores semejantes a
los del coeficiente de Pearson. Tal como sucedió con el coeficiente

Figura 6 Diagramas de dispersión para las series de SPI vs. RDI, SPI vs. SPEI y RDI vs. SPEI para la estación El Sauz (32018), para el periodo de 1961-2012.
Para el caso de estudio, el empleo del SPI y del RDI resultó más adecuado para la caracterización de la sequía meteorológica. Según Gocic y Trajkovic (2014), y Xu et al. (2015), el RDI y el SPI son índices más adecuados que el SPEI para caracterizar la sequía en zonas áridas y semiáridas, lo cual coincide con los resultados de esta investigación.
Por otro lado, cabe destacar que la selección de la función de distribución de probabilidad en el análisis de los índices de sequías, puede influir en los resultados obtenidos, subestimando o sobreestimando los eventos de sequía. Por lo tanto, es conveniente determinar mediante un análisis de frecuencia, la función de distribución que se ajuste mejor a las series de precipitación, precipitación/evapotranspiración y precipitación - evapotranspiración, para evaluar los índices SPI, RDI y SPEI, respectivamente.
Tabla 5 Coeficientes de correlación r y r s entre los índices de sequía SPI, RDI y SPEI.
| Estación | 32001 | 32003 | 32028 | 32018 | 32032 | 32054 | 32052 | 32030 | 32024 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Índice | Coeficiente | r | r s | r | r s | r | r s | r | r s | r | r s | r | r s | r | r s | r | r s | r | r s |
| SPI-3 | RDI-3 | 0.933 | 0.928 | 0.955 | 0.948 | 0.948 | 0.950 | 0.947 | 0.946 | 0.969 | 0.969 | 0.949 | 0.948 | 0.920 | 0.926 | 0.934 | 0.940 | 0.959 | 0.956 |
| SPEI-3 | 0.465 | 0.382 | 0.671 | 0.675 | 0.562 | 0.523 | 0.636 | 0.633 | 0.804 | 0.826 | 0.765 | 0.775 | 0.336 | 0.241 | 0.766 | 0.773 | 0.633 | 0.622 | |
| RDI-3 | SPEI-3 | 0.684 | 0.654 | 0.793 | 0.834 | 0.725 | 0.717 | 0.778 | 0.811 | 0.867 | 0.910 | 0.862 | 0.906 | 0.583 | 0.531 | 0.862 | 0.899 | 0.766 | 0.783 |
| SPI-6 | RDI-6 | 0.943 | 0.933 | 0.958 | 0.931 | 0.947 | 0.935 | 0.949 | 0.929 | 0.962 | 0.939 | 0.952 | 0.936 | 0.944 | 0.941 | 0.943 | 0.911 | 0.964 | 0.941 |
| SPEI-6 | 0.499 | 0.445 | 0.683 | 0.705 | 0.560 | 0.568 | 0.637 | 0.655 | 0.834 | 0.875 | 0.801 | 0.821 | 0.410 | 0.331 | 0.771 | 0.800 | 0.654 | 0.677 | |
| RDI-6 | SPEI-6 | 0.716 | 0.704 | 0.812 | 0.891 | 0.750 | 0.782 | 0.803 | 0.858 | 0.906 | 0.970 | 0.901 | 0.945 | 0.643 | 0.600 | 0.886 | 0.948 | 0.790 | 0.860 |
| SPI-12 | RDI-12 | 0.996 | 0.996 | 0.996 | 0.996 | 0.987 | 0.988 | 0.996 | 0.995 | 0.952 | 0.936 | 0.991 | 0.990 | 0.996 | 0.996 | 0.980 | 0.977 | 0.991 | 0.989 |
| SPEI-12 | 0.964 | 0.980 | 0.982 | 0.986 | 0.950 | 0.951 | 0.981 | 0.985 | 0.926 | 0.912 | 0.976 | 0.981 | 0.927 | 0.940 | 0.952 | 0.959 | 0.962 | 0.960 | |
| RDI-12 | SPEI-12 | 0.978 | 0.992 | 0.993 | 0.997 | 0.986 | 0.985 | 0.993 | 0.997 | 0.992 | 0.997 | 0.991 | 0.998 | 0.952 | 0.960 | 0.991 | 0.997 | 0.987 | 0.989 |
Conclusiones
Los índices multiescalares de sequía meteorológica utilizados en esta investigación permitieron caracterizar las sequías en los últimos 50 años en el estado de Zacatecas, México, obteniendo el número, inicio, final, duración, magnitud, intensidad y categoría de los eventos de sequía.
Los tres índices de sequía aplicados mostraron resultados consistentes en la detección de los eventos de sequía, en particular los de mayor magnitud; con independencia de la escala temporal del índice, su uso permitió un análisis complementario de la variabilidad espacial y temporal de las sequías.
El número de eventos de sequía detectados con los tres índices tuvo menor frecuencia y mayor duración conforme la escala temporal de análisis aumentó. Las tres escalas presentaron eventos de sequía de categoría moderada a extrema, de corta y mediana duración en las escalas de 3 y 6 meses, y de media a larga duración para la escala de 12 meses. El RDI presentó el mayor número de sequías en la escala de tres meses, y en la escala de 6 y 12 meses, el SPI y el SPEI, respectivamente.
El análisis espacial de las sequías muestra que las áreas más afectadas por este fenómeno son la región noroeste, centro y sur del estado. En estas zonas se encuentran ubicadas las principales zonas agrícolas de temporal y de riego de Zacatecas.
Los coeficientes de correlación de Pearson y de Spearman fueron mayores conforme
aumentó la escala de análisis de los índices multiescalares. Los coeficientes
La caracterización de las sequías históricas es importante para generar información relacionada con déficits hídricos durante los periodos de sequía, la cual permite diseñar políticas con el fin de disminuir los daños de eventos futuros de sequía. Dada la importancia del sector agrícola en el estado de Zacatecas, los resultados encontrados pueden ayudar principalmente en la toma de decisiones sobre los patrones de cultivo y la asignación óptima de agua en el Distrito de Riego 034 Estado de Zacatecas.











 texto en
texto en 




