Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Tecnología y ciencias del agua
versión On-line ISSN 2007-2422
Tecnol. cienc. agua vol.9 no.3 Jiutepec may./jun. 2018 Epub 24-Nov-2020
https://doi.org/10.24850/j-tyca-2018-03-03
Articles
Characterization of droughts by comparing three multiscale indices in Zacatecas, Mexico
1Universidad Autónoma de Zacatecas. Unidad Académica de Ingeniería, Zacatecas, Zacatecas, México, ortizgr@uaz.edu.mx
2Universidad Autónoma de Zacatecas. Unidad Académica de Ingeniería, Zacatecas, Zacatecas, México, julio.cardonad@gmail.com
3Universidad Autónoma de Zacatecas. Unidad Académica de Ingeniería, Zacatecas, Zacatecas, México, fidelmprh@uaz.edu.mx
4Universidad Autónoma de Zacatecas. Unidad Académica de Ingeniería, Zacatecas, Zacatecas, México, ampedro@uaz.edu.mx
Drought is one of the most frequent natural disasters to occur in north-central Mexico and its identification and characterization are crucial for mitigating its effects. This study analyzed the evolution of meteorological drought over the period 1961-2012 in the state of Zacatecas, Mexico, using three multiscale indices: the Standardized Precipitation Index (SPI) based on precipitation data, the Reconnaissance Drought Index (RDI), and the Standardized Precipitation-Evapotranspiration Index (SPEI) based on precipitation and evapotranspiration data. The temporal pattern of the drought was analyzed at three time scales (3, 6 and 12 months). The indices were compared using the Pearson and Spearman correlation coefficients. The main dry periods were 1982-1983, 1998-2000, and 2010-2012. At a 3-month scale, the SPI detected the lowest number of drought events (41), with an average duration of 2.5 months; and at 6- and 12-month scales, the RDI detected the lowest number of drought events, 32 and 16, respectively, with an average duration of 3.0 and 6.1 months, respectively. The SPEI detected the greatest number of extreme events at the 3-month scale, and the RDI and the SPI did so at the 6- and 12-month scales, respectively. For the three scales of analysis, the SPEI had the greatest average frequency percentage of severe droughts. The SPI vs RDI had the highest correlation (> 0.92), and the SPI vs SPEI had lowest correlation. The areas that were most affected by droughts were the northwestern, central, and southern regions of Zacatecas, where the principal rainfed and irrigated agriculture areas of the state are located. The findings can primarily help decision-making regarding cropping patterns and the optimal allocation of water in Irrigation District 034 in the state of Zacatecas.
Keywords Meteorological drought; SPI; RDI; SPEI; semiarid regions; severity and duration of droughts; potential evapotranspiration; Pearson and Spearman correlation coefficients
La sequía es uno de los desastres naturales más frecuentes en el centro-norte de México, y su identificación y caracterización son cruciales para tratar de mitigar sus efectos. Se analizó la evolución de las sequías meteorológicas en el estado de Zacatecas, México, para el periodo de 1961 a 2012 utilizando tres índices multiescalares: el Índice de Precipitación Estandarizado (SPI), basado en datos de precipitación; el Índice de Reconocimiento de Sequía (RDI), y el Índice de Precipitación-Evapotranspiración Estandarizado (SPEI), basados en datos de precipitación y evapotranspiración. El patrón temporal de las sequías se analizó en tres escalas de tiempo (3, 6 y 12 meses). Los índices se compararon empleando los coeficientes de correlación de Pearson y de Spearman. Los principales periodos secos fueron 1982-1983, 1998-2000 y 2010-2012. En la escala de tres meses, el SPI detectó el menor número de eventos de sequía (41), con una duración media de 2.5 meses; y en las escalas de 6 y 12 meses, el RDI detectó el menor número de eventos de sequía, 32 y 16, respectivamente, con duración media de 3.0 y 6.1 meses, respectivamente. En la escala de tres meses, el SPEI detectó el mayor número de eventos extremos, y en las escalas de 6 y 12 meses fueron el RDI y el SPI, respectivamente. En las tres escalas de análisis, el SPEI presentó el mayor porcentaje de frecuencia promedio de sequías severas. Los índices SPI vs. RDI presentan la correlación más alta (> 0.92), y el SPI vs. SPEI la correlación más baja. Las áreas más afectadas por las sequías son la región noroeste, centro y sur de Zacatecas, donde se ubican las principales zonas agrícolas de temporal y de riego del estado. Los resultados encontrados pueden ayudar principalmente en la toma de decisiones sobre los patrones de cultivo y la asignación óptima de agua en el Distrito de Riego 034 Estado de Zacatecas.
Palabras clave sequía meteorológica; SPI; RDI; SPEI; regiones semiáridas; severidad y duración de sequías; evapotranspiración potencial; coeficientes de correlación de Pearson y de Spearman
Introduction
Central and northern Mexico are located in the northern latitude high pressure belt. For this reason, these regions are arid and semi-arid, coinciding in latitude with the great deserts of Africa and Asia. Consequently, these regions do not have access to water in sufficient quantities and have historically been affected by droughts. In the 20th century, Mexico experienced four long periods of drought: 1948-1954, 1960-1964, 1970-1978, and 1993-1996, as well as a severe drought in 1998, which mainly affected the northern states (Cenapred, 2007). According to Escalante and Reyes (1998), the state of Zacatecas, located in north-central Mexico, is among the states whose agriculture and livestock was most damaged by the droughts that occurred between 1988 and 1995.
Recently, several droughts of considerable magnitude have been registered, in the years 2000-2003, 2009, and 2011-2012. Between 2000 and 2003, 18 of the 32 Mexican states suffered drought, and the northern states, including Zacatecas, were the most affected. Economic losses reached more than 1 800 million pesos (188 million dollars). Nearly a million hectares of crops were affected, and more than 13 000 head of cattle were lost (Cenapred, 2002; Cenapred, 2003; Cenapred, 2004). In 2009, Mexico suffered the second worst drought in 60 years with damages reaching 3 081 million pesos (229 million dollars) and 384 540 hectares of crops and grasslands were impacted. Zacatecas was among the five states with the largest affected area (Semarnat, 2012). In late 2011 and up to the middle of 2012, more than 60% of Mexico suffered the worst drought in the last 70 years, and its intensity was classified by the North American Drought Monitor (NADM) as severe to exceptional (Semarnat, 2012). Moreover, according to the United States Department of Agriculture (USDA), this drought caused economic losses to the agricultural sector of more than 16 000 million pesos (1 300 million dollars) (Herron, 2013). The state of Zacatecas was the hardest hit by this natural disaster. Thus, it is important to have precise regional knowledge of droughts in the state of Zacatecas in order to establish mitigation measures.
Droughts can have serious, lasting repercussions on human and natural systems, such as humanitarian disasters, economic losses, and stressed natural ecosystems (Touma, Ashfaq, Nayak, Kao, & Diffenbaugh, 2015). Droughts are driven by adverse climate variations and hydrological conditions (Li, Liang, Yu, & Acharya, 2014). Although they are a consequence of a natural reduction in the amount of rainfall in a period, their severity is evaluated in terms of their duration, the season in which they occur, the size of the affected area, and particularly, their impact on human and agricultural activities and the environment (Caparrini & Manzella, 2009). Droughts have been classified into four categories: meteorological, hydrological, agricultural, and socioeconomic (Samaniego, Kumar, & Zink, 2013).
The complexity of defining a drought is due to the difficulty with quantifying its magnitude or severity, since it is typically identified based on its effects on different systems (water resources, agriculture, ecology, economic losses, etc.). However, there is no physical variable that can specifically measure the severity of a drought. The quantification of a drought generally uses drought indices (Asadi-Zarch, Sivikumar, & Sharma, 2015), which are based on data about precipitation, temperature, evapotranspiration, river flows, or other measurable hydrometeorological variables that quantify drought risk. Today, there are many indices for drought quantification. The most used worldwide are the Standardized Precipitation Index (SPI) developed by McKee, Doesken, & Kleist (1993) and the Palmer Drought Severity Index (PDSI) developed by Palmer (1965). The SPI is a probabilistic approach to precipitation, while the PDSI analyzes soil water balance. Recently, the World Meteorological Organization (WMO) presented SPI as the universal drought index (Hayes, Svoboda, Wall, & Widhalm, 2011; WMO, 2012). The main advantage of the SPI is that calculations can be done at different time scales (usually 1, 3, 6, 9, 12, 24, and 48 months), and hydrological variations of precipitation deficits can be represented. However, the SPI does have one disadvantage, namely, it uses only information on precipitation and does not consider other climatological variables that play an important role in the development of a drought event (Teuling et al., 2013). Recently, indices have been developed that incorporate evapotranspiration into the evaluation of droughts. For example, Tsakiris and Vangelis (2005) proposed the Reconnaissance Drought Index (RDI), which analyzes the ratio of accumulated precipitation to potential accumulated evapotranspiration (ETP) from a probabilistic standpoint. Vicente-Serrano, Begueria and López-Moreno (2010) developed the Standardized Precipitation-Evapotranspiration Index (SPEI), which consists of a monthly climate water balance.
Because of the complexity of the drought phenomenon, none of the drought indices can be applied in all regions or to all natural systems. Therefore, to analyze droughts, more than one index should be used, in order to examine the sensitivity and precision of each index and to explore their behavior in specific conditions and for particular purposes. The characterization of a drought event involves identification of its start and end dates, duration, magnitude (severity), and intensity (McKee et al., 1993; Kavalieratou, Karpouzos, & Babajimopoulos, 2012). Other characteristics of droughts include spatial coverage (area) and frequency of occurrence (Kirono, Kent, Hennessy, & Mpelasoka, 2011)
The objectives of this study were to (a) investigate the main characteristics of meteorological droughts in the state of Zacatecas during the period from 1961 to 2012 using the multiscale drought indices SPI, RDI and SPEI; and (b) compare the temporal and spatial behavior of the drought indices used.
Materials and methods
Characteristics of the study area
The state of Zacatecas is located between the coordinates 21º 01’ 00” and 25º 07’ 00” N and 100º 43’ 00” and 104º 22’ 00” W. Its area is 75 284 km 2. The main climate types are arid and semiarid (73%) and temperate subhumid (17%). Mean annual temperature is 17ºC and average annual high and low temperatures are 30ºC (May) and 3ºC (January), respectively. The mean annual precipitation in Zacatecas is 510 mm, with 300 mm in the north and 860 mm in the south. Most of the rainfall occurs in summer (75%), from June to September. The climate of Zacatecas limits agriculture, the main economic activity to which 1.74 million hectares is dedicated; 88% of this area is rainfed.
Climatological information
To identify the drought events, as well as to determine their duration, magnitude, intensities, and frequencies, this study used daily precipitation and temperature data series from 9 weather stations in the state of Zacatecas (Figure 1), taken from the CICLOM database (Conagua, 2014) for the period from January 1, 1961, to December 31, 2012. The geographic descriptors (coordinates and altitude) of the weather stations and the mean annual values corresponding to precipitation, P, and temperature, T, are presented in Table 1.
Table 1 Weather stations and their corresponding mean annual precipitation and temperature.
| Code | Name | Latitude (N) | Longitude (O) | Altitude (m) | Period | Precipitation (mm) | Temperature (ºC) |
|---|---|---|---|---|---|---|---|
| 32052 | San Rafael | 24º 35’ | 102º 06’ | 2 014 | 1961-2012 | 262.8 | 14.4 |
| 32028 | Juan Aldama | 24º 16’ | 103º 23’ | 1 999 | 1961-2012 | 433.0 | 18.0 |
| 32001 | Agua Nueva | 23º 47’ | 102º 09’ | 1 946 | 1961-2012 | 349.1 | 17.7 |
| 32054 | Sombrerete (DGE) | 23º 38’ | 103º 38’ | 2 300 | 1961-2012 | 551.4 | 16.4 |
| 32018 | El Sauz | 23º 16’ | 103º 06’ | 2 096 | 1961-2012 | 414.7 | 16.0 |
| 32003 | Calera | 22º 54’ | 102º 39’ | 2 097 | 1961-2012 | 426.5 | 15.6 |
| 32030 | La Florida | 22º 41’ | 103º 36’ | 1 870 | 1961-2012 | 590.3 | 16.4 |
| 32024 | Guadalupe Victoria | 22º 23’ | 101º 49’ | 2 132 | 1971-2012 | 374.1 | 16.4 |
| 32032 | La Villita | 21º 36’ | 103º 20’ | 1 786 | 1961-2012 | 782.3 | 20.4 |
Methodology
For this study, we used the three drought indices that are most commonly used and well-known worldwide: the Standardized Precipitation Index, the Reconnaissance Drought Index, and the Standardized Precipitation-Evapotranspiration Index. Drought characterization was carried out in six stages: 1) selection and quality control of the climatological information; 2) selection of the scale of analysis; 3) calculation of potential evapotranspiration (ETP); 4) calculation of the SPI, RDI, and SPEI indices at time scales of 3, 6, and 12 months; 5) analysis of drought characteristics; and 6) comparison of the meteorological drought indices. Figure 2 schematically presents the methodological development of the study.
Selection and quality control of the climatological information
A key stage in the analysis of hydroclimatological time series, as in the case of drought analysis, is the data selection and quality control. Selection of the climatological information used is primarily based on four criteria: (1) that the weather station is active, to be able to evaluate the droughts during the last few years; (2) that each weather station has precipitation and temperature records covering at least 40 years; (3) that the percentage of missing data is less than or equal to 15% in order to maintain data representativeness; and (4) that the stations are distributed throughout the study zone so as to have good spatial representation of the drought.
For drought analysis, a preliminary quality control of the precipitation and temperature data series was carried out, checking for homogeneity of the climatological data series and filling missing data. To check for homogeneity of precipitation and temperature data, parametric and non-parametric statistical tests were applied to the annual series. The tests selected were the Student’s t-test, the Cramer test (Mirza, 1997), the Standard Normal Homogeneity Test (SNHT), and the Buishand test (Hänsel, Mederios, Matschullat, Petta, & Mendoça-Silva, 2016).
To select the method for filling in missing data, several methods were tested: polynomial interpolation, arithmetic average, inverse distance, and normal ratio (Tabios III & Salas, 1985; Dingman, 2002). The normal ratio had the best results (Equation (1)):
where
Selection of the scales of drought analysis (k)
The time scale,
This study selected scales of 3, 6, and 12 months for the SPI, RDI, and SPEI indices (SPI-3, SPI-6, SPI-12, RDI-3, etc.), with the aim of obtaining short-, medium-, and relatively long-term perspectives of drought characteristics.
Calculation of potential evapotranspiration (ETP)
To calculate the RDI and SPEI indices, potential evapotranspiration was estimated using the Thornthwaite (1948) method, as proposed by Tsakiris and Vangelis (2005) and Vicente-Serrano et al. (2010). This method of calculating ETP (Equation (2)) is one of the simplest, since it only requires mean monthly precipitation data and the latitude of the site where ETP is to be estimated.
where
where
and
In which
where
The Standardized Precipitation Index (SPI)
The SPI uses precipitation as the only variable for the analysis, and
estimates whether, in a given region and period, there is a deficit or
excess of precipitation relative to normal conditions (Hayes, Svoboda, Wilhite, & Vanyarkho, 1999). The
calculation of the SPI is based on long-term precipitation records. Guttman (1994) points out that
preferably 50 to 60 years or more of records are needed, although other
researchers (Wu, Hayes, Wilhite, &
Svoboda, 2005; Li et
al., 2014) recommend at least 30 years. The SPI is
calculated by fitting an appropriate probability distribution function
(pdf), generally the gamma distribution function, to cumulative monthly
precipitation data for each time scale,
where
where
where
Integrating the gamma density function (Equation (9)), relative to
Considering
Given that the gamma function is not defined for
where
If
Finally, to define the SPI value, the cumulative probability function,
where
A drought event occurs when, at any time scale, SPI is continuously negative and reaches a value of -1.0 or less. It ends when the SPI becomes positive (McKee et al., 1993; Vrochidou & Tsanis, 2012). The SPI values can be easily compared simultaneously on the spatial and temporal dimensions (Lopez-Bustins, Pascual, Pla, & Retana, 2013). Based on the range of SPI values, drought events are classified from mild to extreme (Table 2).
Table 2 Classification of SPI (McKee et al., 1993).
| SPI value | Classification |
|---|---|
| ≥ 2.00 | Extremely wet |
| 1.50 a 1.99 | Severely wet |
| 1.00 a 1.49 | Moderately wet |
| 0 a 0.99 | Mild wet (close to normal) |
| 0 a -0.99 | Mild drought (close to normal) |
| -1.00 a -1.49 | Moderate drought |
| -1.50 a -1.99 | Severe drought |
| ≤ -2.00 | Extreme drought |
The Reconnaissance Drought Index (RDI)
The RDI can be calculated at different time scales and its interpretation is
similar to that of the SPI (Table 2)
(Vicente-Serrano, Van der Schrier,
Beguería, Azorin-Molina, & López-Moreno, 2015; Xu et al., 2015). One
of the most notable theoretical limitations of this drought index is that it
is not valid when the ETP value is equal to zero, a very common situation in
cold regions during winter (Vicente-Serrano
et al., 2015). RDI is expressed in three
ways: the initial value
where
where
Different studies with data from different places and different time scales
have found that, in all cases, the values of
Tigkas (2008) and Asadi-Zarch et al.
(2011) have shown that the RDIst can be better calculated by
fitting the gamma distribution to the distribution of
In our study, the RDI was obtained by fitting the gamma distribution to
The Standardized Precipitation-Evapotranspiration Index
The main limitation of the SPI is that it is based only on precipitation and ignores other variables that affect atmospheric water demand, such as temperature, wind speed, solar radiation, and vapor pressure deficit (McEvoy, Huntington, Abatzoglou, & Edwards, 2012). To overcome this limitation, Vicente-Serrano et al. (2010) developed the SPEI, which combines the PDSI’s sensitivity to changes in the evaporation demand, which is caused by temperature fluctuations and tendencies, with the SPI’s simplicity of calculation and multi-scale nature (Vicente-Serrano et al., 2010; Banimahd & Khalili, 2013; Li et al., 2014).
The SPEI is based on the monthly climatic water balance (precipitation minus
potential evapotranspiration, called series
As a first step to calculate the SPEI, the difference between precipitation
and potential evapotranspiration for month
where
To calculate the SPEI, a three-parameter probability distribution needs to be
used, since for a two-parameter distribution, the variable
where
The log-logistic distribution parameters can be obtained using different methods, of which the L-moments method is the most robust and the easiest to apply (Ahmad, Sinclair, & Werritti, 1988; Singh, Guo, & Yu, 1993).
where
where
The probability distribution of the
Finally, to obtain the SPEI values,
Results and discussion
Here, a drought event was defined as an event for which the values of SPI, RDI, or SPEI are equal to or less than -1.0. We determined the number of drought events and their duration and magnitude for scales of 3, 6, and 12 months at each of the nine stations analyzed.
A general analysis of the drought indices shows that, both locally and regionally, these indices follow the same temporal pattern for the period from 1961 to 2012. According to the SPI, RDI, and SPEI indices, the wettest periods were 1965-1968, 1990-1992, and 2003-2005. The main drought events occurred in 1969-1970, 1982-1983, 1998-2000, and 2010-2012.
The three indices analyzed showed consistent results in detecting the major drought events, in terms of their magnitude and duration (Table 3). The SPE, RDI, and SPEI series were very similar regardless of the time scale. These results indicate that for climate conditions with little interannual variability in temperature, the drought indices analyzed mainly respond to variability in precipitation.
The results of the SPI and RDI indices were similar at the 3- and 6-month scales (SPI-3 and RDI-3; SPI-6, and RDI-6). With SPI-3 and RDI-3 most of the drought periods were detected in the months of January to May, while with SPEI-3 they were detected from April to July. Regarding SPI-6 and RDI-6, most of the dry periods occurred in the months from March to June, while with SPEI-6 they occurred from May to September. For these scales, the SPEI detected droughts several months after the SPI and RDI, because of the relationship that exists between precipitation and temperature during the first months of the year. At the 12-month scale, the results of the three indices were similar, although in the important periods, in terms of duration, magnitude and intensity, SPI-12 and RDI-12 were more similar. According to SPI-12, RDI-12, and SPEI-12, major drought periods occurred in 1962, 1969, 1979, 1982, 1998, 1999, 2000, 2011, and 2012. For most of these years, Campos-Aranda (2014) identified droughts at the Fresnillo weather station in central Zacatecas using the Probabilistic Precipitation Deficit Index, SPI, and RDI. For those same years, Campos-Aranda (2016) also reported annual droughts in a large part of Zacatecas using the aridity index. The most important drought period in terms of intensity occurred between 2011 and 2012.
The evolution of the SPI, RDI, and SPEI series at the 3-month scale (short-term) had a high temporal frequency of periods of drought and moisture. As the time scale increased to 6 and 12 months, the dry and wet periods had a lower temporal frequency and a longer duration (Figure 3). The dry and wet seasons were more clearly defined, especially on the 12-month scale.
Table 3 Maximum values of drought characteristics for all stations and time scales.
| Index | Station | Duration | Severity (Magnitude) | Intensity | |||
|---|---|---|---|---|---|---|---|
| Value | Period | Value | Period | Value | Period | ||
| 32052 | 6 | 12/2010 - 05/2011 | -8.426 | 12/2010 - 05/2011 | -1.483 | 04/1962 - 04/1962 | |
| 32028 | 7 | 12/1988 - 06/1989 | -9.005 | 12/1988 - 06/1989 | -1.361 | 04/1964 - 04/1964 | |
| SPI-3 | 32018 | 6 | 12/2010 - 05/2011 | -9.696 | 12/2010 - 05/2011 | -1.713 | 01/1972 - 02/1972 |
| 32024 | 6 | 12/2000 - 05/2001 | -9.396 | 12/2000 - 05/2001 | -1.574 | 04/1973 - 04/1973 | |
| 32032 | 6 | 12/2002 - 05/2003 | -8.936 | 12/2010 - 04/2011 | -1.787 | 12/2010 - 04/2011 | |
| 32052 | 7 | 12/2010 - 06/2011 | -9.711 | 12/2010 - 06/2011 | -1.483 | 02/1966 - 02/1966 | |
| 32028 | 7 | 12/1988 - 06/1989 | -9.109 | 12/1988 - 06/1989 | -1.361 | 04/1964 - 04/1964 | |
| RDI-3 | 32018 | 6 | 12/2010 - 05/2011 | -9.877 | 12/2010 - 05/2011 | -1.713 | 01/1972 - 02/1972 |
| 32024 | 6 | 12/2000 - 05/2001 | -9.414 | 12/2000 - 05/2001 | -1.574 | 04/1961 - 05/1961 | |
| 32032 | 6 | 12/2010 - 05/2011 | -10.102 | 12/2010 - 05/2011 | -1.787 | 05/1970 - 05/1970 | |
| 32052 | 6 | 05/1974 - 10/1974 | -9.775 | 05/1974 - 10/1974 | -1.900 | 06/1965 - 06/1965 | |
| 32028 | 5 | 04/1982 - 08/1982 | -8.923 | 05/1980 - 08/1980 | -2.231 | 05/1980 - 08/1980 | |
| SPEI-3 | 32018 | 5 | 05/1962 - 09/1962 | -7.463 | 05/1962 - 09/1962 | -2.048 | 05/1990 - 06/1990 |
| 32024 | 4 | 04/1989 - 07/1989 | -7.247 | 04/1989 - 07/1989 | -1.969 | 05/1998 - 06/1998 | |
| 32032 | 4 | 04/2011 - 07/2011 | -9.134 | 04/2011 - 07/2011 | -2.320 | 05/2010 - 06/2010 | |
| 32052 | 10 | 12/1984 - 09/1985 | -14.918 | 12/1984 - 09/1985 | -2.416 | 05/1980 - 05/1980 | |
| 32028 | 6 | 02/1989 - 07/1989 | -10.971 | 02/1989 - 07/1989 | -2.173 | 04/1979 - 05/1979 | |
| SPI-6 | 32018 | 5 | 03/2011 - 07/2011 | -10.564 | 03/2011 - 07/2011 | -2.113 | 03/2011 - 07/2011 |
| 32024 | 6 | 01/2001 - 06/2001 | -12.945 | 01/2001 - 06/2001 | -2.189 | 02/1990 - 05/1990 | |
| 32032 | 4 | 03/2011 - 06/2011 | -8.633 | 03/2011 - 06/2011 | -2.525 | 04/1991 - 05/1991 | |
| 32052 | 15 | 12/1984 - 02/1986 | -20.798 | 12/1984 - 02/1986 | -2.437 | 05/1980 - 05/1980 | |
| 32028 | 5 | 03/1989 - 07/1989 | -10.325 | 03/1989 - 07/1989 | -2.094 | 04/1991 - 06/1991 | |
| RDI-6 | 32018 | 6 | 03/2011 - 08/2011 | -12.613 | 03/2011 - 08/2011 | -2.166 | 02/1976 - 06/1976 |
| 32024 | 6 | 01/2001 - 06/2001 | -13.096 | 01/2001 - 06/2001 | -2.243 | 04/1981 - 05/1981 | |
| 32032 | 4 | 03/2011 - 06/2011 | -9.290 | 03/2011 - 06/2011 | -2.622 | 04/1991 - 05/1991 | |
| 32052 | 6 | 06/1974 - 11/1974 | -10.257 | 06/1974 - 11/1974 | -1.877 | 07/1989 - 11/1989 | |
| 32028 | 6 | 06/1980 - 11/1980 | -12.848 | 06/1980 - 11/1980 | -2.141 | 06/1980 - 11/1980 | |
| SPEI-6 | 32018 | 7 | 05/2011 - 11/2011 | -12.414 | 05/2011 - 11/2011 | -1.881 | 07/1962 - 11/1962 |
| 32024 | 7 | 04/1989 - 10/1989 | -12.949 | 04/1989 - 10/1989 | -1.850 | 04/1989 - 10/1989 | |
| 32032 | 9 | 03/2011 - 11/2011 | -16.395 | 03/2011 - 11/2011 | -1.822 | 03/2011 - 11/2011 | |
| 32052 | 40 | 06/1985 - 09/1988 | -65.884 | 06/1985 - 09/1988 | -1.837 | 11/1975 - 05/1976 | |
| 32028 | 18 | 07/2011 - 12/2012 | -30.437 | 07/2011 - 12/2012 | -2.074 | 06/1978 - 06/1978 | |
| SPI-12 | 32018 | 18 | 02/2011 - 07/2012 | -38.158 | 02/2011 - 07/2012 | -2.120 | 02/2011 - 07/2012 |
| 32024 | 20 | 08/1989 - 03/1991 | -35.080 | 08/1989 - 03/1991 | -1.754 | 08/1989 - 03/1991 | |
| 32032 | 23 | 02/2011 - 12/2012 | -44.154 | 02/2011 - 12/2012 | -1.920 | 02/2011 - 12/2012 | |
| 32052 | 40 | 06/1985 - 09/1988 | -61.101 | 06/1985 - 09/1988 | -1.832 | 11/1975 - 05/1976 | |
| 32028 | 14 | 07/2011 - 08/2012 | -24.325 | 07/2011 - 08/2012 | -1.835 | 06/1982 - 04/1983 | |
| RDI-12 | 32018 | 18 | 02/2011 - 07/2012 | -36.955 | 02/2011 - 07/2012 | -2.053 | 02/2011 - 07/2012 |
| 32024 | 20 | 08/1989 - 03/1991 | -35.433 | 08/1989 - 03/1991 | -1.772 | 08/1989 - 03/1991 | |
| 32032 | 23 | 02/2011 - 12/2012 | -52.654 | 02/2011 - 12/2012 | -2.289 | 02/2011 - 12/2012 | |
| 32052 | 25 | 12/1961 - 12/1963 | -40.618 | 12/1961 - 12/1963 | -1.625 | 12/1961 - 12/1963 | |
| 32028 | 12 | 06/1980 - 05/1981 | -22.007 | 06/1980 - 05/1981 | -1.935 | 06/1982 - 04/1983 | |
| SPEI-12 | 32018 | 18 | 02/2011 - 07/2012 | -30.817 | 02/2011 - 07/2012 | -1.814 | 08/1962 - 06/1963 |
| 32024 | 24 | 06/1989 - 05/1991 | -38.493 | 06/1989 - 05/1991 | -1.629 | 12/1971 - 11/1972 | |
| 32032 | 26 | 11/2010 - 12/2012 | -50.699 | 11/2010 - 12/2012 | -1.950 | 11/2010 - 12/2012 | |
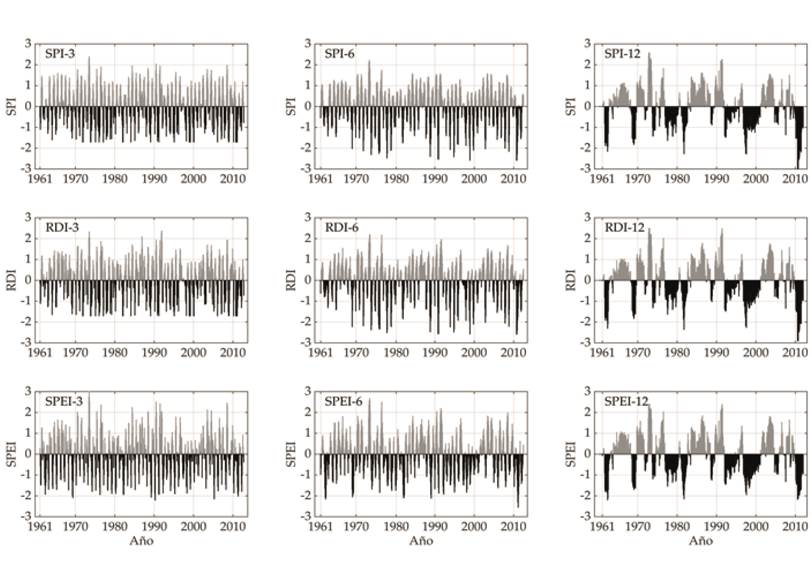
Figure 3 Temporal evolution of drought at 3-, 6-, and 12-month scales at the El Sauz station (32018).
Mean drought characteristics
Table 4 presents a summary of the number of drought events and the mean duration of drought periods for short-, medium-, and long-term time scales, determined with the three drought indices evaluated. The mean number of drought episodes decreased with longer time scales.
The average number of drought events at a short-term time scale varied from 36 - 48 months for SPI-3, from 41 - 49 for RDI-3, and from 38 - 52 months for SPEI-3. The mean duration of the drought events ranged from 2.3 to 2.9, 2.2 to 2.7, and 2.0 to 3.2 months for SPI-3, RDI-3, and SPEI-3, respectively. At 70% of the weather stations, the drought event of largest magnitude reached the severe drought category with SPI-3 and RDI-3, while with SPEI-3, it reached the category of extreme drought at 90% of the weather stations. The longest duration of drought periods registered with SPI-3 and RDI-3 ranged from 5 to 8 months, and from 4 to 7 months for SPEI-3.
Over the last two decades, the most intense drought events occurred at the 3-month scale. According to SPI-3 and RDI-3, these events were from February to May of 1999 and from January to May of 2011, and according to SPEI-3 they occurred from May to July of 2011 and from May to June of 1998.
For the 6-month scale, the drought events detected by the three indices were relatively similar. Average droughts ranged from 28 to 41, 26 to 39, and 27 to 39 months for SPI-6, RDI-6, and SPEI-6, respectively. The mean duration of these events ranged from 2.6 to 3.1 months for SPI-6, from 2.7 to 3.2 months for RDI-6, and from 2.9 to 4.1 months for SPEI-6. With SPI-6 and RDI-6, the most intense events reached the category of extreme drought at all the stations; with SPEI-6 only 20% reached this category and the rest of the stations registered severe drought. According to SPEI-6, the longest durations of dry periods were very similar among the stations, ranging from 6 to 9 months, while according to SPI-6 and RDI-6, the range was greater, from 4 to 15 months.
According to SPI-6, RDI-6, and SPEI-6, the northeastern part of Zacatecas had major droughts in the 1970s and 1980s, in terms of magnitude and intensity. During the 1990s and the first decade of 2000, major droughts occurred in the central and southern parts of the state.
Table 4 Number and mean duration of the drought events determined by SPI, RDI, and SPEI for the period 1961-2012. (The records from this station is for the period 1971-2012. Mean duration is shown in parenthesis.)
| Station | SPI-3 | RDI-3 | SPEI-3 | SPI-6 | RDI-6 | SPEI-6 | SPI-12 | RDI-12 | SPEI-12 |
|---|---|---|---|---|---|---|---|---|---|
| 32052 | 43 (2.4) | 44 (2.2) | 38 (3.2) | 28 (3.1) | 30 (3.0) | 27 (4.1) | 16 (6.8) | 14 (8.1) | 19 (6.1) |
| 32028 | 36 (2.8) | 41 (2.7) | 47 (2.3) | 41 (2.6) | 39 (2.7) | 34 (2.9) | 21 (5.1) | 16 (5.8) | 19 (5.1) |
| 32001 | 37 (2.9) | 42 (2.5) | 45 (2.6) | 32 (3.0) | 26 (3.2) | 34 (3.2) | 10 (6.2) | 11 (5.6) | 19 (4.6) |
| 32054 | 42 (2.3) | 46 (2.3) | 47 (2.1) | 38 (3.1) | 34 (3.0) | 36 (3.1) | 13 (8.9) | 12 (9.4) | 13 (9.1) |
| 32018 | 48 (2.3) | 49 (2.4) | 51 (2.2) | 37 (2.9) | 36 (2.8) | 35 (3.0) | 18 (5.7) | 19 (5.1) | 18 (5.8) |
| 32003 | 41 (2.3) | 41 (2.3) | 48 (2.0) | 39 (2.8) | 33 (3.0) | 33 (3.3) | 19 (5.2) | 20 (5.0) | 21 (5.4) |
| 32024* | 31 (2.8) | 34 (2.5) | 40 (2.1) | 26 (3.1) | 26 (3.0) | 28 (3.3) | 16 (5.4) | 19 (4.8) | 18 (5.3) |
| 32032 | 47 (2.5) | 46 (2.6) | 44 (2.1) | 38 (2.8) | 37 (2.9) | 39 (2.9) | 18 (5.7) | 15 (6.7) | 13 (8.2) |
| 32030 | 44 (2.5) | 47 (2.4) | 52 (2.0) | 34 (3.1) | 31 (3.1) | 37 (3.1) | 19 (4.8) | 21 (4.2) | 18 (5.7) |
At the 6-month scale, RDI-6 detected the longest drought period (15 months), which occurred in the northern region of Zacatecas (station 32052). The longest drought detected by SPI-6 and RDI-6 was at station 32001 (northern Zacatecas), lasting 13 months, from June 1987 to June 1988. SPEI-6 detected a drought for this same period and station, but in two subperiods, one 6 months long (from July to December 1987) and another lasting 3 months (May to July 1988). The longest drought detected with SPEI-6 was 9 months at stations 32032 and 32054, from March to November of 2011, in southern and west-central Zacatecas, respectively. In this same period, SPI-6 and RDI-6 detected a period of drought of only 4 months, from March to June of 2011.
Regarding the 12-month time scale (medium- and long-term), the average number of drought events was similar for the three indices, ranging from 10 to 21 for SPI-12, from 11 to 21 for RDI-12, and from 13 to 21 for SPEI-12. The mean duration of the drought events ranged from 4.8 to 8.9 months for SPI-12, from 4.2 to 9.4 months for RDI-12, and from 4.6 to 9.1 months for SPEI-12. At this scale, with SPI-12 and RDI-12 the most intense events reached the category of extreme drought at 70% of the stations, and 30% severe drought, while with SPEI-12 only 10% of the stations showed extreme drought and the remaining 90% reported severe drought. The longest dry periods were similar with SPI-12 and RDI-12, and ranged from 16 to 40 and from 14 to 40 months, respectively, while the periods were shorter with SPEI-12, ranging from 12 to 27 months.
During the 52 years of climatological records analyzed in the state of Zacatecas, the SPI detected the most intense droughts on the annual time scale, coinciding with the results obtained by Campos-Aranda (2014, 2015), who analyzed droughts with SPI and RDI in central Zacatecas. With the 3- and 6-month time scales, the most intense droughts were detected by SPEI and RDI, respectively.
The most intense droughts at the three time scales occurred between 1998 and 2011. RDI and SPEI also identified extreme droughts in 1974, 1979, 1982, and 1989. Figure 4 shows the spatial distribution of the SPI, RDI, and SPEI for the month with the greatest drought at the three time scales analyzed. With the 3-month time scale, SPI-3 and RDI-3 identified April 2011 as the month with the highest drought intensity. These indices have a spatial behavior that is practically equal (Figures 4a and 4b). Most of Zacatecas (82%) suffered severe drought and only 8% extreme drought. The most intense drought detected by SPEI-3 occurred in June 2011, with extreme drought in 59% of the state, mainly in the central part (Figure 4c). At the 6-month scale, April 2011 was also the month of greatest drought intensity according to SPI and RDI; extreme drought occurred in practically the entire state (Figures 4d and 4e). The SPEI-6 identified July 2011 as the month with the greatest drought; most of the territory of Zacatecas underwent extreme drought (49%) and severe drought (39%). Extreme drought occurred mainly in central and northeastern Zacatecas. At the 12-month scale, September 2011 was identified by the three indices as the month with the highest drought intensity. SPI-12 and RDI-12 had similar spatial behavior, identifying around 55% of Zacatecas with extreme drought (Figures 4g and 4h), mainly in the south and west of the state. SPEI-12 identified extreme drought in 33% of Zacatecas, in the same regions as did SPI-12 and RDI-12, but in a smaller area.
Drought frequency
Drought frequency was analyzed using the different drought classes (Table 2) related to the values of the drought indices (SPI, RDI, SPEI). At the 3-month scale, for the drought indices analyzed, the average time (percentage of average frequency) of dry and wet periods was 17.1 and 16.9%, respectively. Normal precipitation conditions were present 66.0% of the time. SPI-3 and RDI-3 showed a higher frequency of moderate droughts (12.5 and 12.2%, respectively) than SPEI-3, while the frequency of severe droughts was lower for SPI-3 and RDI-3 (4.1 and 4.8%, respectively) than for SPEI-3. Of the three indices, SPI-3 and RDI-3 identified a lower number of extreme droughts. Figure 5a shows the frequency percentage of dry and wet periods for SPI-3, RDI-3, and SPEI-3. With SPI-3 and RDI-3, only the west-central region of the study area (station 32054) had extreme droughts (14 and 15 events, respectively), while with SPEI-3, all the stations had extreme drought events, ranging from 3 to 16 events at stations 32052 and 32032, in northern and southern Zacatecas, respectively.
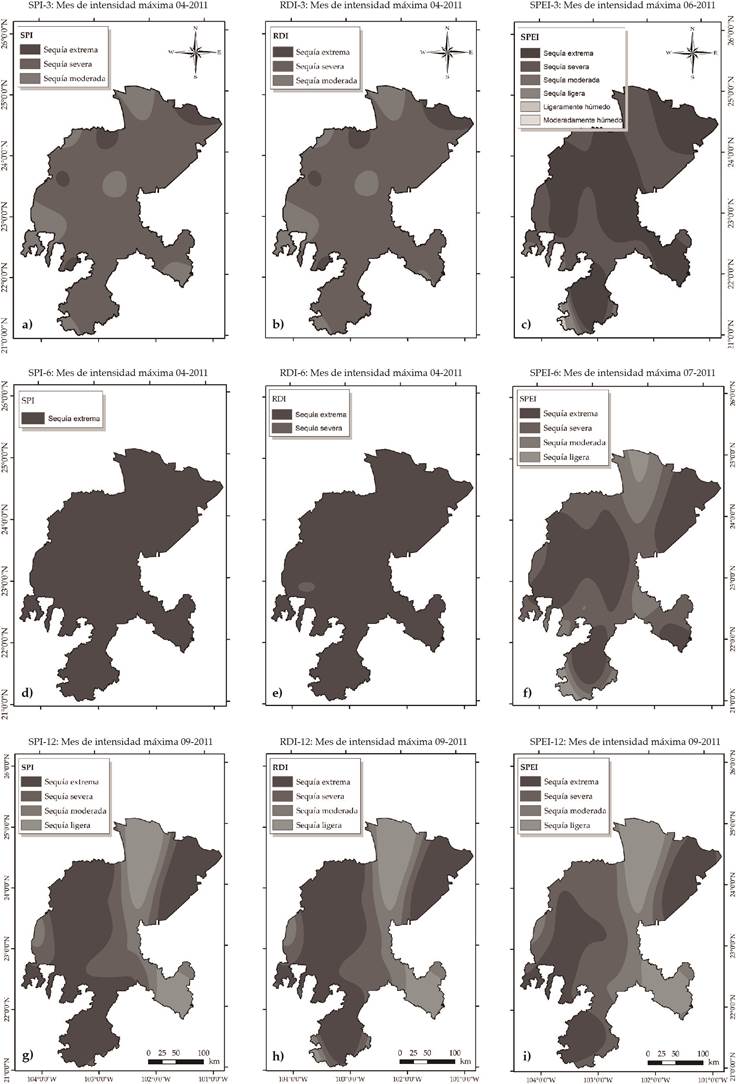
Figure 4 Spatial distribution of the SPI, RDI, and SPEI indices for the month with the most intense drought at scales of 3, 6, and 12 months.
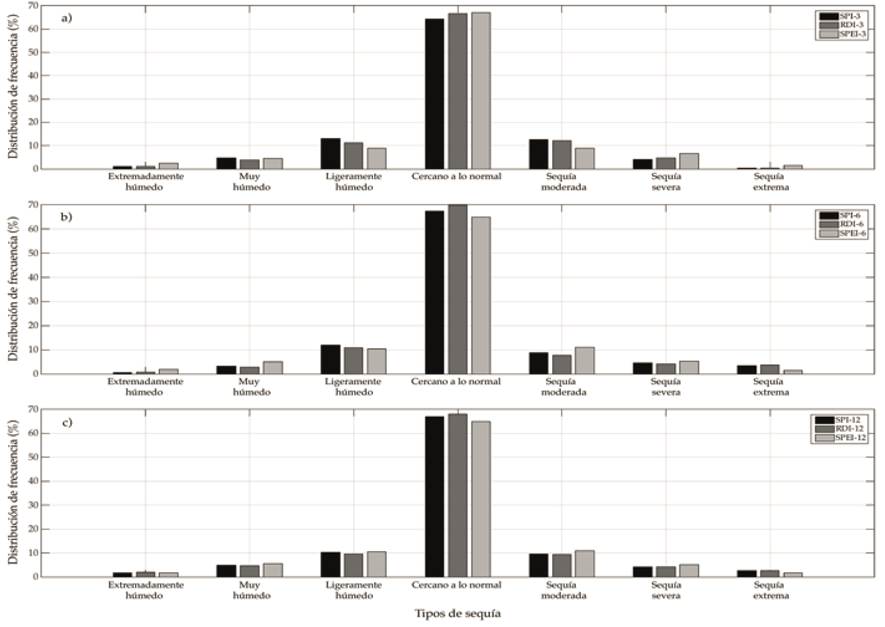
Figure 5 Frequency distribution of the values of the SPI, RDI, and SPEI indices: a) 3-month scale; b) 6-month scale; and c) 12-month scale for the period 1961-2012.
At the 6-month scale, according to the three multiscale indices, normal precipitation conditions were present an average of 67.4% of the time. The frequency of dry events was 16.7% and that of wet events was 15.9%. SPEI-6 resulted in a higher frequency of moderate droughts (11.0%) than SPI-6 and RDI-6 (8.7 and 7.7%, respectively). The same occurred with severe droughts (Figure 5b). However, SPI-6 and RDI-6 presented a higher frequency of extreme droughts than SPEI-6: 3.4 and 3.8% respectively. With SPI-6 and RDI-6, 26 and 29 extreme droughts in central Zacatecas were detected (stations 32018 and 32030), while with SPEI-6 the highest number of extreme droughts detected was 15, which occurred in the north (station 32001). Finally, at the 12-month scale, the average frequency percentage of normal, wet, and dry events was 66.6, 16.9, and 16.5%, respectively. The frequency of droughts with SPI-12, RDI-12, and SPEI-12 was 16.3, 15.8, and 17.4%, respectively. The behavior and values of the frequency of the different classes of droughts for SPI-12, RDI-12, and SPEI-12 were similar to those detected by SPI-6, RDI-6, and SPEI-6. And SPEI-12 presented a higher frequency of moderate and severe droughts than SPI-12 and RDI-12. The opposite occurred for extreme droughts, as seen in Figure 5c. With SPI-12 and RDI-12, 23 and 22 extreme drought events were detected at station 32032 (southern Zacatecas), while with SPEI-12, the highest number of extreme drought events was 17, and occurred at station 32001 (northern Zacatecas).
Correlation of the drought indices
Considering the three time scales and the nine stations analyzed, the SPI and RDI were the mostly highly correlated indices, with correlation coefficients (r) ranging from 0.920 to 0.996. SPI and SPEI had the lowest correlation coefficients, which ranged from 0.336 to 0.982. Figure 6 shows the general trend of the relationships between SPI vs RDI, SPI vs SPEI, and RDI vs SPEI at the 3-, 6-, and 12-month time scales, with dispersion diagrams for the series of indices at El Sauz station (32018), located in the central region of Zacatecas.
At the 3-month scale, the correlation coefficients (r) for SPI-3 vs RDI-3 ranged from 0.920 to 0.969, while SPI-3 vs SPEI-3 and RDI-3 vs SPEI-3 ranged from 0.336 to 0.804 and from 0.583 to 0.867, respectively. In general, the correlations for the 6-month scale were slightly higher than for the 3-month scale, ranging from 0.943 to 0.964 for SPI-6 vs RDI-6, from 0.410 to 0.834 for SPI-6 vs SPEI-6, and from 0.643 to 0.906 for RDI-6 vs SPEI-6. At the 12-month scale, the correlation coefficients ranged from 0.952 to 0.996 for SPI-12 vs RDI-12, from 0.926 to 0.982 for SPI-12 vs SPEI-12, and from 0.952 to 0.993 for RDI-12 vs SPEI-12. For the scales and stations analyzed, the smaller the scale, the lower the correlation between indices (Table 5). At the 3- and 6-month scales, the lowest correlations were in the north of the state (station 32052) and the highest in the south (station 32032).
The Spearman correlation coefficients (Table
5) were similar to those of the Pearson correlation coefficients.
As for coefficient
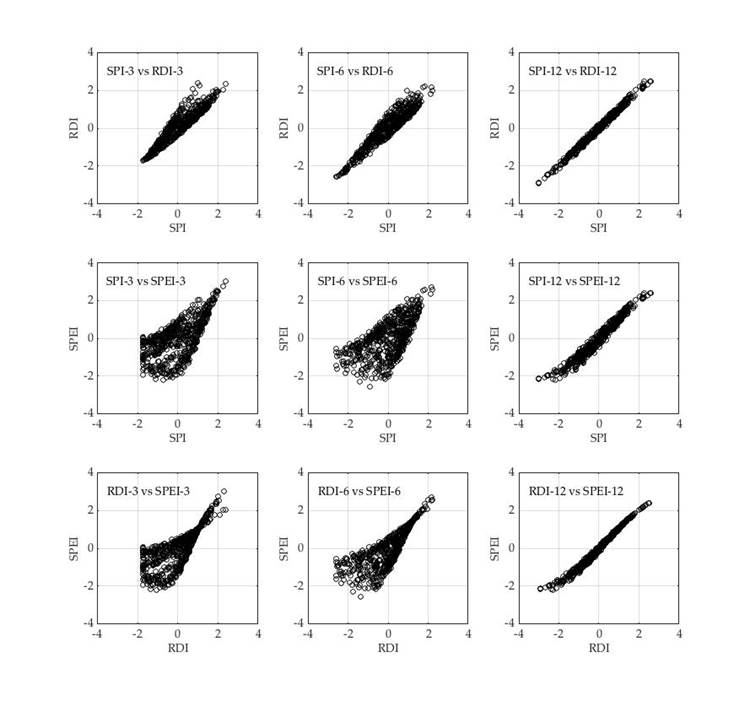
Figure 6 Dispersion diagrams for the SPI vs RDI, SPI vs SPEI, and RDI vs SPEI series for the El Sauz station (32018), period 1961-2012.
In this study, SPI and RDI were more suitable for characterizing meteorological drought. According to Gocic and Trajkovic (2014) and Xu et al. (2015), RDI and SPI are more suitable indices than SPEI for characterizing drought in arid and semiarid regions. Our results coincide.
Moreover, selection of the probability distribution function for the analysis of drought indices may affect the results, underestimating or overestimating drought events. Therefore, it is helpful to use a frequency analysis to determine the distribution function that best fits the precipitation, precipitation/evapotranspiration, and precipitation - evapotranspiration series when evaluating the SPI, RDI, and SPEI indices, respectively.
Table 5 Correlation coefficients r and r s for the SPI, RDI, and SPEI drought indices.
| Station | 32001 | 32003 | 32028 | 32018 | 32032 | 32054 | 32052 | 32030 | 32024 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Index | Coefficient | r | r s | r | r s | r | r s | r | r s | r | r s | r | r s | r | r s | r | r s | r | r s |
| SPI-3 | RDI-3 | 0.933 | 0.928 | 0.955 | 0.948 | 0.948 | 0.950 | 0.947 | 0.946 | 0.969 | 0.969 | 0.949 | 0.948 | 0.920 | 0.926 | 0.934 | 0.940 | 0.959 | 0.956 |
| SPEI-3 | 0.465 | 0.382 | 0.671 | 0.675 | 0.562 | 0.523 | 0.636 | 0.633 | 0.804 | 0.826 | 0.765 | 0.775 | 0.336 | 0.241 | 0.766 | 0.773 | 0.633 | 0.622 | |
| RDI-3 | SPEI-3 | 0.684 | 0.654 | 0.793 | 0.834 | 0.725 | 0.717 | 0.778 | 0.811 | 0.867 | 0.910 | 0.862 | 0.906 | 0.583 | 0.531 | 0.862 | 0.899 | 0.766 | 0.783 |
| SPI-6 | RDI-6 | 0.943 | 0.933 | 0.958 | 0.931 | 0.947 | 0.935 | 0.949 | 0.929 | 0.962 | 0.939 | 0.952 | 0.936 | 0.944 | 0.941 | 0.943 | 0.911 | 0.964 | 0.941 |
| SPEI-6 | 0.499 | 0.445 | 0.683 | 0.705 | 0.560 | 0.568 | 0.637 | 0.655 | 0.834 | 0.875 | 0.801 | 0.821 | 0.410 | 0.331 | 0.771 | 0.800 | 0.654 | 0.677 | |
| RDI-6 | SPEI-6 | 0.716 | 0.704 | 0.812 | 0.891 | 0.750 | 0.782 | 0.803 | 0.858 | 0.906 | 0.970 | 0.901 | 0.945 | 0.643 | 0.600 | 0.886 | 0.948 | 0.790 | 0.860 |
| SPI-12 | RDI-12 | 0.996 | 0.996 | 0.996 | 0.996 | 0.987 | 0.988 | 0.996 | 0.995 | 0.952 | 0.936 | 0.991 | 0.990 | 0.996 | 0.996 | 0.980 | 0.977 | 0.991 | 0.989 |
| SPEI-12 | 0.964 | 0.980 | 0.982 | 0.986 | 0.950 | 0.951 | 0.981 | 0.985 | 0.926 | 0.912 | 0.976 | 0.981 | 0.927 | 0.940 | 0.952 | 0.959 | 0.962 | 0.960 | |
| RDI-12 | SPEI-12 | 0.978 | 0.992 | 0.993 | 0.997 | 0.986 | 0.985 | 0.993 | 0.997 | 0.992 | 0.997 | 0.991 | 0.998 | 0.952 | 0.960 | 0.991 | 0.997 | 0.987 | 0.989 |
Conclusions
The multiscale meteorological drought indices used in this study made it possible to characterize the droughts that occurred over the last 50 years in the state of Zacatecas, Mexico, providing the number, beginning, end, duration, magnitude, intensity, and category of the events.
The three drought indices consistently detected drought events, particularly those of greatest magnitude, regardless of the time scale of the index. They also enabled conducting a complementary analysis of the spatial and temporal variability of the droughts.
The events detected with the three indices had a lower frequency and longer duration as the time scale of the analysis increased. The three scales presented drought events characterized as moderate and extreme, which were of short and medium duration at the 3- and 6-month scales, and of medium to long duration for the 12-month scale. The RDI detected a higher number of droughts at the 3-month scale, while SPI and SPEI did so at the 6- and 12-month scales, respectively.
The spatial analysis of the droughts shows that the areas that were most affected by this phenomenon were the northwestern, central, and southern parts of the state. The principal rainfed and irrigated agricultural regions of Zacatecas are located in these areas.
The Pearson and Spearman correlation coefficients were higher as the scale of the
indices increased. The
Characterization of historical droughts is important for generating information related to water deficits during periods of drought, since it can contribute to designing policies aimed at reducing damage from future drought events. Given the importance of the agricultural sector in the state of Zacatecas, the findings of this study may support decision-making mainly regarding crop patterns and optimal water allocation in Irrigation District 034 in the state of Zacatecas.
Acknowledgements
Our thanks to the Zacatecas Council on Science, Technology and Innovation (COZCYT), Mexico, for funding the FOMIX - CONACYT Project “Study of meteorological droughts in the state of Zacatecas and development of a low-cost prototype for monitoring a system of potable water supply”, project code ZAC-2013-C02-201203.
REFERENCES
Ahmad, M. I., Sinclair, C. D., & Werritti, A. (1988). Log-logistic flood frequency analysis. Journal of Hydrology, 98, 205-224. [ Links ]
Angelidis, P., Maris, F., Kotsovinos, N., & Hrissanthou, V. (2012). Computation of drought index SPI with alternative distribution functions. Water Resources Management, 26, 2453-2473. [ Links ]
Asadi-Zarch, M. A., Malekinezhad, H., Mobin, M. H., Dastorani, M. T., & Kousari, M. R. (2011). Drought monitoring by reconnaissance drought index (RDI) in Iran. Water Resources Management, 25, 3485-3504. [ Links ]
Asadi-Zarch, M. A., Sivakumar, B., & Sharma, A. (2015). Droughts in a warming climate: A global assessment of Standardized Precipitation Index (SPI) and Reconnaissance Drought Index (RDI). Journal of Hydrology, 526, 183-195. [ Links ]
Banimahd, S. A., & Khalili, D. (2013). Factors influencing Markov chains predictability characteristics, utilizing SPI, RDI, EDI and SPEI drought indices in different climatic zones. Journal of Water Resources Management, 27, 3911-3928. [ Links ]
Cai, W., Zhang, Y., Yao, Y., & Chen, Q. (2015). Probabilistic analysis of drought spatiotemporal characteristics in the Beijing-Tianjin-Hebei metropolitan area in China. Atmosphere, 6, 431-450. [ Links ]
Campos-Aranda, D. F. (2014). Comparación de tres métodos estadísticos para detección y monitoreo de sequías meteorológicas. Agrociencia, 48, 463-476. [ Links ]
Campos-Aranda, D. F. (2015). Contraste de los índices DPP, SPI y RDI para clasificación de sequías, en la estación climatológica Zacatecas, México. Tecnología y Ciencias del Agua, 6(1), 183-193. [ Links ]
Campos-Aranda, D. F. (2016). Estudio de sequías meteorológicas anuales por medio del índice de aridez, en el estado de Zacatecas, México. Ingeniería, Investigación y Tecnología, 17(3), 405-417. [ Links ]
Caparrini, F., & Manzella, F. (2009). Hydrometeorological and vegetation indices for the drought monitoring system in Tuscany Region, Italy. Advanced in Geosciences, 17, 105-110. [ Links ]
Centro Nacional de Prevención de Desastres, Cenapred. (2002). Impacto socioeconómico de los principales desastres ocurridos en la República Mexicana en el año 2001. Serie Impacto Socioeconómico de los Desastres Naturales. México, DF: Centro Nacional de Prevención de Desastres, Secretaría de Gobernación. [ Links ]
Centro Nacional de Prevención de Desastres, Cenapred. (2003). Impacto socioeconómico de los principales desastres ocurridos en la República Mexicana en el año 2002. Serie Impacto Socioeconómico de los Desastres Naturales. México, DF: Centro Nacional de Prevención de Desastres, Secretaría de Gobernación . [ Links ]
Centro Nacional de Prevención de Desastres, Cenapred. (2004). Impacto socioeconómico de los principales desastres ocurridos en la República Mexicana en el año 2003. Serie Impacto Socioeconómico de los Desastres Naturales. México, DF: Centro Nacional de Prevención de Desastres, Secretaría de Gobernación . [ Links ]
Centro Nacional de Prevención de Desastres, Cenapred. (2007). Fascículo Sequías. México, DF: Centro Nacional de Prevención de Desastres, Secretaría de Gobernación . [ Links ]
Comisión Nacional del Agua, Conagua. (2014). Base de datos en el sistema CLIma COMputarizado (CLICOM). México, DF: Servicio Meteorológico Nacional, Comisión Nacional del Agua. [ Links ]
Dingman, S. L. (2002). Physical Hydrology. New Jersey, USA: Prentice Hall. [ Links ]
Edwards, D. C., & McKee, T. B. (1997). Characteristics of 20th century drought in the United States at multiple time scales (155 pp.) (Climatology Report 97-2). Fort Collins, Colorado, USA: Department of Atmospheric Science, Colorado State University. [ Links ]
Escalante, C., & Reyes, L. (1998). Identificación y análisis de sequías en la Región Hidrológica Número 10, Sinaloa. Ingeniería Hidráulica en México, 13(2), 23-43. [ Links ]
Gocic, M., & Trajkovic, S. (2014). Drought characterisation based on water surplus variability index. Water Resources Management, 28, 3179-3191. [ Links ]
Guttman, N. B. (1994). On the sensitivity of sample L moments to sample size. Journal of Climate, 7, 1026 -1029. [ Links ]
Haan, C. T. (1977). Statistical Methods in Hydrology. Iowa, USA: The Iowa State University Press. [ Links ]
Hänsel, S., Medeiros, D. M., Matschullat, J., Petta, R. A., & de Mendonça-Silva, I. (2016). Assessing homogeneity and climate variability of temperature and precipitation series in the capitals of North-Eastern Brazil. Frontiers in Earth Science, 4. DOI: 10.3389/feart.2016.00029 [ Links ]
Hayes, M., Svoboda, M., Wall, N., & Widhalm, M. (2011). The Lincoln declaration on drought indices: Universal meteorological drought index recommended. Bulletin American Meteorology Society, 92, 485-488. [ Links ]
Hayes, M. J., Svoboda, M. D., Wilhite, D. A., & Vanyarkho, O. V. (1999). Monitoring the 1996 drought using the standardized precipitation index. Bulletin of the American Meteorological Society, 80, 429-438. [ Links ]
Herron, C. A. (2013). Agua y cambio climático en México 2007-2012: Análisis y recomendaciones a futuro. Recuperado de http://www.conagua.gob.mx/CONAGUA07/Contenido/Documentos/AyCCMex2007-2012.pdf [ Links ]
Kavalieratou, S., Karpouzos, D. K., & Babajimopoulos, C. (2012). Drought analysis and short-term forecast in the Aison River Basin (Greece). Natural Hazards and Earth System Sciences, 12, 1561-1572. [ Links ]
Kirono, D. G. C., Kent, D. M., Hennessy, K. J., & Mpelasoka, F. (2011). Characteristics of Australian droughts under enhanced greenhouse conditions: Results from 14 global climate models. Journal of Arid Environments, 75, 566-575. [ Links ]
Kousari, M. R., Dastorani, M. T., Niazi, Y., Soheili, E., Hayatzadeh, M., & Chezgi, J. (2014). Trend detection of drought in arid and semi-arid regions of Iran based on implementation of reconnaissance drought index (RDI) and application of non-parametrical statistical method. Water Resources Management, 28, 1857-1872. [ Links ]
Li, B., Liang, Z., Yu, Z., & Acharya, K. (2014). Evaluation of drought and wetness episodes in a cold region (Northeast China) since 1898 with different drought indices. Natural Hazards, 71, 2063-2085. [ Links ]
Lopez-Bustins, J. A., Pascual, D., Pla, E., & Retana, J. (2013). Future variability of droughts in three Mediterranean catchments. Natural Hazards, 69, 1405-1421. [ Links ]
López-Moreno, J. I., Vicente-Serrano, S. M., Zabalza, J., Beguería, S., Lorenzo-Lacruz, J., Azorin-Molina, C., & Morán-Tejeda, E. (2013). Hydrological response to climate variability at different time scales: A study in the Ebro basin. Journal of Hydrology, 477, 175-188. [ Links ]
McEvoy, D. J., Huntington, J. L., Abatzoglou, J. T., & Edwards, L. M. (2012). An evaluation of multiscalar drought indices in Nevada and Eastern California. Earth Interactions, 16, 1-18. [ Links ]
McKee, T. B., Doesken, N. J., & Kleist, J. (1993). The relationship of drought frequency and duration to time scales. 8th Conference on Applied Climatology Series 3-7, National Climatic Data Center, Ashville, N.C. [ Links ]
Mirza, M. M. Q. (1997). Hydrological changes in the Ganges system in Bangladesh in the post-Farakka period. Hydrological Sciences-Journal, 42, 613-631. [ Links ]
Palmer, W. C. (1965). Meteorological drought (58 pp.) (Research Paper No. 45). Washington, DC, USA: Commerce Weather Bureau. [ Links ]
Samaniego, L., Kumar, R., & Zink, M. (2013). Implications of parameter uncertainty on soil moisture drought analysis in Germany. Journal of Hydrometeorolgy, 14, 47-68. [ Links ]
Secretaría de Medio Ambiente y Recursos Naturales, Semarnat. (2012). Informe de la situación del medio ambiente en México, compendio de estadísticas ambientales indicadores clave y de desempeño ambiental. México, DF: Secretaría de Medio Ambiente y Recursos Naturales. [ Links ]
Singh, V. P., Guo, H., & Yu, F. X. (1993). Parameter estimation for 3-parameter log-logistic distribution (LLD3) by Pome. Stochastic Hydrology and Hydraulics, 7, 163-177. [ Links ]
Tabios III, G. Q., & Salas, J. D. (1985). A comparative analysis of techniques for spatial interpolation of precipitation. Journal of the American Water Resources Association, 21, 365-380. [ Links ]
Teuling, A. J., Van Loon, A. F., Seneviratne, S. I., Lehner, I., Aubinet, M., Heinesch, B., Bernhofer, C., Grünwald, T., Prasse, H., & Spank, U. (2013). Evapotranspiration amplifies European summer drought. Geophysical Research Letters, 40, 2071-2075. [ Links ]
Thornthwaite, C. W. (1948). An approach toward a rational classification of climate. Geography Review, 38, 55-94. [ Links ]
Tigkas, D. (2008). Drought characterisation and monitoring in regions of Greece. European Water, 23/24, 29-39. [ Links ]
Touma, D., Ashfaq, M., Nayak, M. A., Kao, S. C., & Diffenbaugh, N. S. (2015). A multi-model and multi-index evaluation of drought characteristics in the 21st century. Journal of Hydrology, 526, 196-207. [ Links ]
Tsakiris, G., Pangalou, D., & Vangelis, H. (2007). Regional drought assessment based on the Reconnaissance Drought Index (RDI). Water Resources Management, 21, 821-833. [ Links ]
Tsakiris, G., & Vangelis, H. (2005). Establishing a drought index incorporating evapotranspiration. European Water, 9, 3-11. [ Links ]
Vicente-Serrano, S. M., Beguería, S., & López-Moreno, J. I. (2010). A multi-scalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index (SPEI). Journal of Climate, 23, 1696-1718. [ Links ]
Vicente-Serrano, S. M., Van der Schrier, G., Beguería, S., Azorin-Molina, C., & López-Moreno, J. I. (2015). Contribution of precipitation and reference evapotranspiration to drought indices under different climates. Journal of Hydrology, 526, 42-54. [ Links ]
Vrochidou, A.-E. K., & Tsanis, I. K. (2012). Assessing precipitation distribution impacts on droughts on the island of Crete. Natural Hazards Earth System Science, 12, 1159-1171. [ Links ]
World Meteorological Organization, WMO. (2012). Standardized precipitation index user guide. In: Svoboda, M., Hayes, M., & Wood, D. (eds.) (WMO-No. 1090). Geneva, Switzerland: World Meteorological Organization. [ Links ]
Wu, H., Hayes, M. J., Wilhite, D. A., & Svoboda, M. D. (2005). The effect of the length of record on the standardized precipitation index calculation. International Journal Climatology, 25, 505-520. [ Links ]
Xu, K., Yang, D., Yang, H., Li, Z., Qin, Y., & Shen, Y. (2015). Spatio-temporal variation of drought in China during 1961-2012: A climatic perspective. Journal of Hydrology, 526, 253-264. [ Links ]
Zelen, M., & Severo, N. C. (1965). Probability Functions. In: M. Abramowitz, & I. Stegun (eds.), Handbook of Mathematical Functions (pp. 925-995). New York, USA: Dover Publications. [ Links ]
Received: November 14, 2016; Accepted: January 18, 2018











 texto en
texto en 




