Introducción
Se estima que alrededor de 300 millones de personas han sido afectadas desde la década de 1990 por desastres naturales (Trivedi, Singh, & Indian, 2015). Según el Grupo Intergubernamental de Expertos sobre el Cambio Climático (IPCC, por sus siglas en inglés) se han observado desviaciones en los patrones meteorológicos promedio del mundo, con una mayor frecuencia de eventos extremos de precipitación (UN-HABITAT, 2011). En este sentido, las inundaciones se encuentran entre los peligros naturales más recurrentes y devastadores (Ouma & Tateishi, 2014). Las inundaciones corresponden a 50% de los desastres relacionados con el agua, por encima de hambrunas, sequías y epidemias (Hernández-Uribe, Barrios-Piña, & Ramírez, 2017).
La aceleración del crecimiento poblacional y los cambios en el uso de suelo aumentan la vulnerabilidad ante las inundaciones, incluyendo mortalidad y morbilidad, desplazamiento, y daño a cultivos, así como a la infraestructura y propiedad (Dewan, 2015). Existe una relación directa entre urbanización y cambios en las características hidrológicas, incluyendo disminución de la infiltración, aumento de escorrentía y altura de las inundaciones que, aunado al crecimiento de la población y a la acumulación de activos de valor, agravan el riesgo de inundación en zonas urbanas (Ouma & Tateishi, 2014). Por lo anterior, las cuencas urbanas resultan más vulnerables a estos fenómenos, sobre todo por los procesos de origen antrópico propios de su dinámica (UN-HABITAT, 2011).
La principal característica de la precipitación en zonas áridas y semiáridas consiste en tormentas que se intensifican con rapidez, provocando inundaciones repentinas (Pourreza, Samadi, Akhoond, & Ghahraman, 2016). En estas regiones habita alrededor de 20% de la población total y representan un 30% del área mundial (Sivakumar, Das, & Brunini, 2005).
Este estudio se realiza en el Río Nuevo, dentro de la cuenca transfronteriza del Salton Sea, ubicada en la región semiárida del Delta del río Colorado, colindante con la frontera entre los estados de Baja California, México, y California, Estados Unidos (The Salton Sea Authority, 2015). El Río Nuevo es un componente intraurbano, ubicado en la ciudad de Mexicali, Baja California, México, que conduce, además de escurrimientos superficiales derivados de eventos locales por precipitación, aguas residuales de origen agrícola, aguas provenientes de procesos industriales y aguas negras.
La importancia del estudio de eventos extremos de precipitación por tormentas de alta intensidad y corta duración en zonas áridas y semiáridas estriba en la capacidad de daños que estos fenómenos pueden ocasionar en la población, y en la infraestructura urbana y agrícola, así como en las actividades de importancia socioeconómica. En el caso del condado Imperial, en California, Estados Unidos, a partir de 1958 y hasta 2006 se habían declarado cuatro estados de emergencias debido a inundaciones, presentando severos daños en la infraestructura hidráulica, agrícola y carretera (Imperial County, 2013). La situación en Mexicali es distinta, pues la zona con mayor riesgo de inundación se presenta en su núcleo urbano, en particular en el Río Nuevo, donde se ha desarrollado infraestructura educativa, comercial, de gobierno y asentamientos humanos.
Tomando como referencia lo anterior y entendiendo que en la evaluación del riesgo de inundación es importante una base científica para la gestión del riesgo de desastres, el objetivo de este estudio es determinar las áreas de inundación del cauce principal del Río Nuevo, caracterizando una tormenta de diseño en condiciones estándar, y con periodos de retorno de 20, 50, 100 y 500 años, a través del acoplamiento de los modelos hidrológico e hidráulico. Esto incluye el empleo de un análisis regional de frecuencia (ARF), con enfoque en los L-momentos que, según Wallis, Shaefer, Barker y Taylor (2007), ha demostrado la fiabilidad de las estimaciones de magnitud de ocurrencia de precipitación.
Referente a los modelos hidrológicos, desde el desarrollo del método racional por Mulvany (1850), se inició la evolución de los mismos, pasando por modelos simples (concentrados) para eventos hasta el desarrollo de modelos distribuidos para simulaciones eventuales y continuas (Vargas-Castañeda, Ibáñez-Castillo, & Arteaga-Ramírez, 2015). Los modelos usados para predecir etapas y flujos en ríos están bien adoptados en la práctica. La gama actual de métodos de modelado fluvial puede dividirse en tres grupos: 1) el proveniente de las ecuaciones de Saint-Venant, incluyendo HEC-RAS; 2) modelos basados en datos observados, donde la mayoría de los parámetros carece de una interpretación física directa, y 3) un grupo que se encuentra entre los dos anteriores e incluye modelos conceptuales que emanan de la ecuación de continuidad (Wolfs, Meert, & Willems, 2015).
Para el análisis hidrológico de este estudio se optó por el empleo de un modelo semidistribuido, como lo es el Hydrologic Modelig System (HEC-HMS), mismo que ha sido ampliamente utilizado para evaluar efectos en los hidrogramas ante posibles escenarios de cambio climático, tipo de uso de suelo, diseño y gestión de obras hidráulicas, así como en la delimitación de zonas inundables (López et al., 2012). Por otro lado, la simulación hidráulica se realizó mediante el software River Analysis System (HEC-RAS), que cuenta con una serie de componentes de análisis unidimensional y bidimensional de flujo en ríos que permite simular el flujo de agua en un modelo 2D, a fin de determinar la llanura de inundación.
Según el estado del arte referente a la modelación hidrológica e hidráulica, la mayoría se realiza de forma independiente, limitando la capacidad de los modelos para pronosticar niveles de inundación debido a errores ocasionados por la manipulación y transferencia de la información (Rodríguez, González, Medina, Pardo, & Santos, 2007). Así, este estudio propone un modelo integral a través de la puesta en marcha de un modelo hidrológico, alimentado con los resultados del ARF, con el enfoque de los L-momentos, y su acoplamiento con un modelo hidráulico, empleando las herramientas de modelado de HEC-HMS y HEC-RAS.
Área de estudio
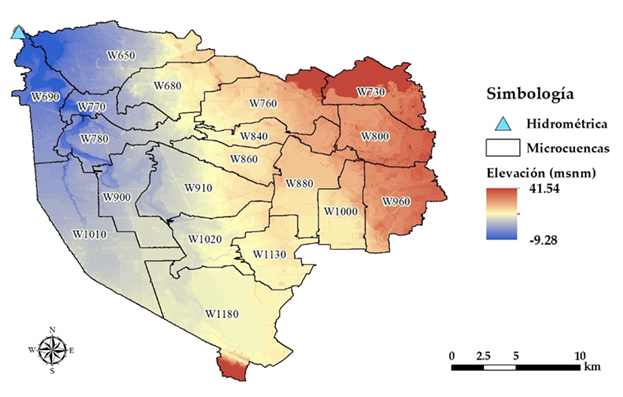
El Río Nuevo se encuentra en una cuenca transfronteriza al noroeste de México, constituida por la participación de distintos núcleos urbanos. Al norte colinda con el condado Imperial, en California, Estados Unidos; y al sur, con la ciudad de Mexicali, Baja California, México (Figura 1).
Cabe mencionar que este río pertenece al delta del río Colorado, que actualmente abastece a más de 30 millones de personas en Estados Unidos y México (Rodríguez-Burgueño, Shanafield, & Ramírez-Hernández, 2017). El río Colorado suministra agua a los estados de Arizona, California, Colorado, Nuevo México, Nevada, Utah y Wyoming, en Estados Unidos, y a los estados de Baja California y Sonora, en México, suministrando agua para regar casi 22 257 km² de campos agrícolas y generando más de 4 200 megawatts de generación eléctrica (U.S Department of the Interior Bureau of Reclamation, 2012). Según los datos del Instituto Nacional de Estadística e Informática (INEGI), referidos en el Censo de Población y Vivienda del año 2010, la población total en Mexicali era de 936 826 habitantes, representando 29.7% de la población total del estado de Baja California.
La superficie de la subcuenca del Río Nuevo, que trasvasa en la frontera de ambos países, es de 2 066.69 km2 y cuenta con una pendiente media de 9.61%. La longitud de su cauce principal es de 47 270 m y su pendiente es de 3.063% (INEGI, 2017). Cabe mencionar que este estudio considera la sección del Río Nuevo con una longitud de 14.17 km, ubicada geográficamente en la coordenadas UTM-WGS84-Z11N a los 3 608 660.30 m norte y 645 613.80 m oeste.
Materiales y métodos
Se desarrolló un modelo hidrológico para obtener un gasto de diseño estimado en diferentes periodos de retorno, bajo el esquema del análisis regional de frecuencia, con el enfoque de los L-momentos. Los resultados alimentaron el modelado hidrológico e hidráulico de la cuenca del Río Nuevo para identificar las zonas de inundación sobre el cauce principal de la cuenca. La preparación e interpretación de los datos del modelo para el procesamiento y la visualización de datos geoespaciales se facilitó con el uso de un sistema de información geográfico (SIG) (Heimhuber, 2013). Se utilizaron las extensiones HEC-GeoHMS y HEC-GeoRAS para la preparación de los archivos de entrada del modelo, incluyendo los registros históricos de precipitación de 35 estaciones meteorológicas y los registros de caudal de una estación hidrométrica ubicada en el trasvase del Río Nuevo, en la frontera con Estados Unidos. En el caso de México, los registros históricos de precipitación se obtuvieron a través del Extractor Rápido de Información climatológica (ERIC III) del Instituto Mexicano de Tecnología del Agua (IMTA) y la Comisión Nacional del Agua (Conagua). En el caso de los registros de Estados Unidos, se utilizaron los datos obtenidos durante el periodo correspondiente a los años de 1930 a 2016, del archivo de datos climáticos de California (CalClim, por sus siglas en inglés). En la Figura 2 se muestra de manera esquemática la metodología implementada para este estudio.

Figura 2 Diagrama del modelo hidrológico e hidráulico basado en SIG, con tormenta de diseño obtenida a través del análisis regional de frecuencia (modificado a partir de Heimhuber, 2013).
Análisis regional de frecuencia con el enfoque de los L-momentos
La mayoría de los procedimientos de análisis regional de frecuencia intenta ajustar a los datos una distribución, cuya forma se especifica a partir de un número finito de parámetros indeterminados del momento de la muestra. En particular, la asimetría (skewness) y la curtosis (kurtosis) se utilizan de modo frecuente para juzgar la cercanía de una muestra observada a una distribución postulada. Sin embargo, las estadísticas son insatisfactorias debido a que están algebraicamente delimitadas, con límites que dependen del tamaño de la muestra; en muestras pequeñas o moderadas, es inusual que asimetría y curtosis de la muestra tomen un valor cercano a los valores poblacionales (Hosking & Wallis, 1997).
Los L-momentos o momentos lineales son un sistema alterno a los métodos tradicionales de los momentos convencionales, que caracterizan las formas de las distribuciones de probabilidad y determinan los parámetros de distribución. Según Hosking y Wallis (1997), los L-momentos se consideran combinaciones lineales de los momentos ponderados. Si bien los L-momentos son un desarrollo relativamente reciente dentro de las estadísticas, forman la base de una teoría matemática y pueden utilizarse para facilitar el proceso de estimación en el análisis regional de frecuencia.
La metodología del ARF utilizada en el presente estudio, con enfoque en los L-momentos, se basa en los trabajos de Wallis et al. (2007), y Schaefer, Barker, Taylor y Wallis (2006), referida por Núñez-Cobo Verbist, Ramírez-Hernández, & Hallack-Alegría (2010), y consta de cuatro etapas: 1) selección de los datos; 2) identificación de regiones homogéneas; 3) selección de la distribución de frecuencia, y 4) estimación de la función de cuantiles.
Selección de los datos
El análisis comienza con la categorización de los sitios en arreglos de
posibles regiones homogéneas utilizando el criterio de discordancia. Dado
que el número de estaciones en las regiones puede variar y la serie de datos
es relativamente pequeña, se consideró analizar los valores críticos de
discordancia recomendados por Hosking y
Wallis (1997), según la expresión:
Tabla 1 Valores críticos de discordancia (D i ) según Hosking y Wallis (1997).
| Número de sitios | Valor crítico | Número de sitios | Valor crítico |
|---|---|---|---|
| 5 | 1.333 | 11 | 2.632 |
| 6 | 1.648 | 12 | 2.757 |
| 7 | 1.917 | 13 | 2.869 |
| 8 | 2.140 | 14 | 2.971 |
| 9 | 2.329 | 15 | 3 |
| 10 | 2.491 |
Identificación de regiones homogéneas
Se utilizó el criterio de estacionalidad y magnitud de la precipitación media anual para el agrupamiento de estaciones. Las medidas de heterogeneidad utilizadas han sido desarrolladas como indicadores del grado de heterogeneidad en las relaciones de los L-momentos para un grupo de mediciones (Schaefer, Barker, Taylor, & Wallis, 2006). El criterio de homogeneidad en este estudio se basa en el trabajo de Wallis et al. (2007), que sugiere los rangos presentados en la Tabla 2.
Tabla 2 Valores críticos de heterogeneidad actualizados (modificado de Núñez-Cobo et al., 2010).
| Heterogeneidad | Wallis et al., 2007 |
|---|---|
| Homogénea | H < 2 |
| Posiblemente heterogénea | 2 < H < 3 |
| Heterogénea | H > 3 |
Las estadísticas H1 y H2 miden la variabilidad relativa del coeficiente de
L-variación (L-Cv, en inglés) y L-Skewness (equivalente al coeficiente de
asimetría convencional) observadas (Núñez-Cobo et al., 2010) para sitios en una subregión, calculada
según la siguiente expresión propuesta (Hosking & Wallis, 1997):
Estas medidas compararon la variabilidad observada con la esperada de una muestra mayor tomada de una región homogénea, representada por la distribución Kappa, según la propuesta de Hosking y Wallis de 1997 (Schaefer et al., 2006). Para este estudio, uno de los criterios utilizados en la integración de regiones homogéneas fue que las estaciones que la integran no presenten propiedades para hacerlas discordantes con las demás que la conforman.
Selección de la distribución de frecuencia
Después de la identificación de las regiones homogéneas, se identificó la
distribución de probabilidad apropiada para describir el comportamiento de
los datos climáticos de interés. La distribución de frecuencia se eligió
basándose en el diagrama de los L-momentos-ratio y la medida de bondad de
ajuste
Tabla 3 Distribuciones de probabilidad.
| Normal generalizada |
|
|
| Pearson tipo III |
|
|
| Generalizadade valor extremo |
|
|
| Kappa de cuatro parámetros |
|
Límite superior es: |
Estimación de la función de cuantiles
Una vez identificada la distribución de probabilidad para la región
homogénea, se determinaron los cuantiles para diferentes periodos de retorno
usando el método Índice de Avenidas, el cual se expresa como
Modelo hidrológico
Las simulaciones hidrológicas se realizaron empleando la herramienta HEC-HMS 3.2 del Hydrologic Engineering Center, representando el proceso de lluvia escorrentía de manera simplificada, simulando el hidrograma que se produce en un determinado punto de la red fluvial, como consecuencia de un episodio de precipitación (López et al., 2012). El modelo en HEC-HMS consideró cuatro componentes: 1) modelo de la cuenca; 2) modelo meteorológico, que indicó la precipitación de entrada requerida por un elemento de la subcuenca; 3) especificación de control con el cual se determinó el inicio y periodo de simulación, y 4) datos de entrada utilizados para proporcionar las variables hidrológicas, como datos de series de tiempo (USACE, 2016).
Determinación de los parámetros de tipo de uso de suelo
La modelación del escurrimiento se basó en el método del Número de Curva (CN) del Servicio de Conservación de Suelos (SCS). Este método se basa en la ecuación de balance de agua, la cual dentro del HEC-HMS estima la precipitación en exceso o efectiva en función de la precipitación acumulada, cobertura del suelo, uso del suelo, y humedad antecedente (Magaña-Hernández, Bá, & Guerra-Cobián, 2013). A fin de determinar con mayor precisión el CN, se obtuvieron los tipos de suelo, el tamaño de sus áreas y su porcentaje de superficie en la zona. Para ello se procesaron 1 500 polígonos con un SIG, sobreponiendo la capa de uso de suelo del Instituto Nacional de Geografía Estadística e Informática (INEGI) a las imágenes obtenidas a través de la plataforma Google Earth. Después, para la definición del CN, se consideraron los valores de la tabla de regiones semiáridas del Natural Resources Conservation Service (NRCS, 1986). Finalmente, se realizó una calibración del modelo hidrológico ajustando el CN, ya que esta variable es el parámetro más sensible (López et al., 2012).
En las especificaciones de control del HEC-HMS se definió el lapso y la fecha
de la ejecución de la simulación, siendo el modelo meteorológico la
representación de la precipitación. El modelo de cuenca se preparó con la
extensión HEC-GeoHMS utilizando la herramienta de fusión de microcuencas,
siguiendo las restricciones de adyacencia y confluencia para facilitar el
manejo de la información espacial. Los resultados del modelo comprendieron
hidrogramas de escorrentía para cada subcuenca, así como representaciones
gráficas y numéricas de precipitaciones, pérdidas y escurrimiento directo.
Por su parte, el tiempo de concentración se calculó con el método de
Kirpich, donde
Delimitación de subcuenca y microcuencas
Una cuenca hidrográfica suele ser delineada como varias subcuencas antes de aplicar el análisis con el HEC-HMS (Patel, 2009). Por lo tanto, la delimitación de las cuencas y redes de drenaje fueron obtenidas utilizando un MDE generado a partir de datos de elevación de alta resolución (LiDAR) de 5 x 5 metros (INEGI, 2010) mediante un SIG.
Modelo hidráulico
Los modelos hidráulicos se utilizaron para simular el comportamiento del flujo en el canal principal y la llanura de inundación del Río Nuevo (Alaghmand, Abdullah, Abustan, & Vosoogh, 2010). Los gastos de diseño de escorrentía generados, se utilizaron como entrada para el modelado en HEC-RAS. La geometría del río fue procesada usando la extensión del HEC-GeoRAS. La realización del modelo hidráulico se constituyó por tres procedimientos fundamentales, como se presenta a continuación.
Preproceso
Se utilizaron los datos geométricos del modelo hidráulico, conformados por el eje del río, secciones transversales, distancia de separación entre secciones, puntos de control, así como el coeficiente de Manning y coeficientes de contracción/expansión.
Proceso-simulación hidráulica con HEC-RAS
Durante la etapa del proceso se establecieron las condiciones de frontera aguas arriba y aguas abajo en la modalidad de flujo permanente. Cabe mencionar que debido a la falta de referencia del nivel del agua se optó por la condición de frontera de tirante crítico (USACE, 2016). Posteriormente se definió el régimen de flujo mixto, a fin de correr la modelación y como parte de este apartado, finalmente se llevó a cabo la calibración del modelo mediante la relación caudal-tirante de agua. El caudal se obtuvo por medio de mediciones in situ, utilizando un velocímetro Doppler acústico y los resultados fueron utilizados para ajustar el modelo matemático de tal manera que reproduzca el fenómeno en estudio (Parhi, Sankhua, & Roy, 2012).
Posproceso
Una vez calibrado el modelo hidráulico se elaboraron mapas de inundación (profundidad) para los diferentes escenarios de flujo. El modelado hidráulico en esta investigación se realizó sin considerar la infraestructura del embovedado del Río Nuevo debido a que en regiones áridas y semiáridas los eventos de inundaciones repentinas son causados por tormentas de alta intensidad y corta duración con alto grado de variabilidad espacial. Estas tormentas suelen presentar crecidas intensas en tiempos muy cortos incluso para cuencas grandes, lo que resulta en cantidades significativas de sedimentos transportados, afectando la infraestructura hidráulica de las instalaciones aguas abajo (Maksimovic, 2001). La modelación hidráulica ―con una extensión de 14.17 km del cauce principal del Río Nuevo, incluyendo el cuerpo lagunar al sur de la ciudad― se analizó mediante 143 secciones transversales distribuidas en intervalos aproximados a los 100 metros.
Resultados y discusión
El estado del arte indica que la generación espacial de la escorrentía en las zonas áridas y semiáridas no es uniforme. Sin embargo, los mecanismos de precipitación dominantes son usualmente tormentas de alta intensidad y corta duración (Wang, Zhang, & Baddo, 2016), condiciones que se cumplen en el área de estudio. Cabe destacar que este trabajo es el primero con tales características que se realiza en la zona, acoplando el modelo hidrológico con el hidráulico, por lo que se espera que sus resultados sean usados como referencia para análisis posteriores.
Análisis regional de frecuencias
Debido a la limitada infraestructura en estaciones meteorológicas y disponibilidad de registros de precipitación en México, el enfoque probabilístico del análisis regional de frecuencia se contempla como una opción válida para estimar la ocurrencia de un evento de precipitación extremo, que será empleado como dato de entrada de un modelo hidrológico. Según los resultados del ARF, se definieron 20 estaciones en la cuenca del Salton Sea consideradas homogéneas (Tabla 4). Seleccionándose la distribución Pearson Tipo III, que fue validada con las funciones Normal Generalizada y Generalizada de Valor Extremo (The Salton Sea Authority, 2015).
Tabla 4 Estaciones de la región homogénea utilizada en el estudio.
| Estación | Latitud norte | Longitud oeste | PMA | L-CV | L-skew | L-kurt | Discordancia (Di) |
|---|---|---|---|---|---|---|---|
| Brawley | 634781.34 | 3647110.12 | 47.1 | 0.366 | 0.242 | 0.175 | 0.26 |
| Bataquez | 681308.65 | 3603156.81 | 36.7 | 0.413 | 0.227 | 0.144 | 1.48 |
| Calexico | 643996.85 | 3617742.02 | 44.7 | 0.357 | 0.171 | 0.139 | 0.33 |
| Col. Rodríguez | 684677.21 | 3588577.52 | 36.1 | 0.402 | 0.183 | 0.174 | 1.75 |
| Deep Canyon Lab | 557860.08 | 3723635.24 | 84.4 | 0.315 | 0.278 | 0.224 | 1.82 |
| Desert Resort RG | 578003.43 | 3721116.77 | 50.8 | 0.334 | 0.212 | 0.155 | 0.19 |
| Ejido Islitas | 696293.9 | 3581476.88 | 46.0 | 0.361 | 0.234 | 0.236 | 1.14 |
| El Centro 2 | 634674.78 | 3627480.63 | 45.3 | 0.323 | 0.112 | 0.083 | 2.00 |
| Hayfield Pump PL | 627051.03 | 3730180.46 | 65.1 | 0.345 | 0.211 | 0.135 | 0.32 |
| Imperial Airport | 633815.99 | 3635564.07 | 43.1 | 0.317 | 0.144 | 0.122 | 1.00 |
| Indio Fire Station | 538732.66 | 3729969.65 | 50.7 | 0.382 | 0.237 | 0.103 | 1.93 |
| Mecca 2 | 585664.6 | 3714972.54 | 47.8 | 0.386 | 0.175 | 0.148 | 0.90 |
| Mxli (Río Nuevo) | 644499.45 | 3615420.52 | 49.2 | 0.313 | 0.208 | 0.174 | 0.53 |
| Mxli C. Agrícola | 617926.28 | 3602097.2 | 68.7 | 0.354 | 0.239 | 0.214 | 0.48 |
| Niland | 637453.84 | 3683078.33 | 44.5 | 0.358 | 0.265 | 0.222 | 0.79 |
| Ocotillo 2 | 593590.88 | 3623570.42 | 66.5 | 0.333 | 0.186 | 0.194 | 0.66 |
| Ocotillo Wells | 580855.45 | 3668250.7 | 43.5 | 0.310 | 0.147 | 0.123 | 1.11 |
| Palm Springs | 545342.18 | 3743082.29 | 81.2 | 0.343 | 0.253 | 0.125 | 1.85 |
| Presa Morelos | 712686.4 | 3620860.17 | 33.9 | 0.387 | 0.225 | 0.161 | 0.48 |
| Yuma Valley | 713970.32 | 3622219.06 | 49.2 | 0.317 | 0.212 | 0.217 | 0.99 |
Después se determinaron los cuantiles correspondientes a los Tr de 20, 50, 100 y 500 años, respectivamente, que se presentan en la Tabla 5.
Tabla 5 Cuantiles correspondientes a los periodos de retorno de 20, 50, 100 y 500 años.
| Cuantil | Periodos de retorno | Normal Generalizada | Generalizada de Valor Extremo | Pearson Tipo III | Kappa |
|---|---|---|---|---|---|
| 0.950 | 20.00 | 2.25 | 2.25 | 2.26 | 2.26 |
| 0.980 | 50.00 | 2.79 | 2.81 | 2.75 | 2.79 |
| 0.990 | 100.00 | 3.20 | 3.25 | 3.10 | 3.19 |
| 0.998 | 500.00 | 4.21 | 4.36 | 3.91 | 4.16 |
Características de los modelos hidrológico e hidráulico
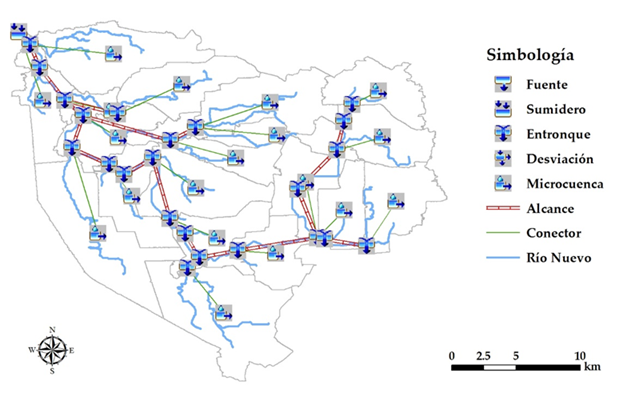
Se obtuvieron 20 microcuencas definidas durante el preproceso en HEC-GeoHMS, las cuales cuentan con una extensión variable para un área total de 562 km². El punto de interés fue ubicado en la salida del Río Nuevo, en el trasvase a California, Estados Unidos, como se muestran en la Figura 3.
Una vez definidas las características físicas de la cuenca, el proyecto fue exportado al HEC-HMS, como se muestra en la Figura 4.
Posteriormente se definieron los datos de entrada de los métodos de pérdida, transformación y enrutamiento, a fin de establecer los parámetros del modelo donde después se analizaron los diferentes periodos de retorno. Por su parte, los gastos máximos en las simulaciones sirvieron de base para el análisis hidráulico (Tabla 6). Cabe señalar que para aumentar la precisión del CN se propuso la abstracción mediante un SIG de los diferentes tipos de uso de suelo, a fin de disminuir los errores por la generalización de los datos propuestos en los manuales.
Tabla 6 Datos de entrada del modelo: número de curva (CN); tiempo de concentración (TC); abstracción inicial (Ia); retención máxima (S), y lag por microcuenca (entradas); además, salidas del modelo: área de drenaje (km²) y gastos máximos (m³/s) por periodo de retorno analizado.
| Microcuenca | Entradas | Salidas | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| CN | TC Kirpich (horas) | Lag Time (min) | S | Ia | Área de drenaje (km²) | Gasto máximo | ||||
| Tr 20 | Tr 50 | Tr 100 | Tr 500 | |||||||
| W650 | 86 | 10.58 | 380.82 | 41.35 | 8.27 | 45.10 | 8.50 | 12.20 | 14.50 | 20.60 |
| W680 | 82 | 12.13 | 436.81 | 55.76 | 11.15 | 29.67 | 4.30 | 6.40 | 7.80 | 11.50 |
| W690 | 82 | 8.28 | 297.91 | 55.76 | 11.15 | 24.09 | 3.50 | 5.20 | 6.30 | 9.40 |
| W730 | 64 | 6.22 | 223.92 | 142.88 | 28.58 | 25.12 | 0.10 | 0.40 | 0.60 | 1.50 |
| W760 | 68 | 10.38 | 373.61 | 119.53 | 23.91 | 37.02 | 1.30 | 2.60 | 3.60 | 6.40 |
| W770 | 88 | 10.54 | 379.48 | 34.64 | 6.93 | 14.49 | 3.10 | 4.40 | 5.10 | 7.20 |
| W780 | 86 | 9.19 | 330.93 | 41.35 | 8.27 | 24.89 | 4.70 | 6.70 | 8.00 | 11.40 |
| W800 | 70 | 11.41 | 410.78 | 108.86 | 21.77 | 26.32 | 0.40 | 0.90 | 1.40 | 2.70 |
| W810 | 86 | 1.36 | 49.01 | 41.35 | 8.27 | 0.29 | 0.10 | 0.10 | 0.10 | 0.10 |
| W840 | 72 | 12.53 | 451.02 | 98.78 | 19.76 | 15.79 | 0.80 | 1.40 | 1.80 | 3.10 |
| W860 | 88 | 10.26 | 369.23 | 34.64 | 6.93 | 16.67 | 3.60 | 5.00 | 5.90 | 8.20 |
| W880 | 72 | 12.31 | 443.21 | 98.78 | 19.76 | 27.47 | 0.70 | 1.40 | 2.00 | 3.60 |
| W900 | 77 | 11.69 | 420.96 | 75.87 | 15.17 | 27.40 | 2.70 | 4.40 | 5.50 | 8.50 |
| W910 | 82 | 11.84 | 426.12 | 55.76 | 11.15 | 37.76 | 5.50 | 8.20 | 9.90 | 14.70 |
| W960 | 68 | 10.80 | 388.98 | 119.53 | 23.91 | 29.76 | 0.30 | 0.80 | 1.30 | 2.60 |
| W1000 | 76 | 9.75 | 350.98 | 80.21 | 16.04 | 20.44 | 0.80 | 1.40 | 1.90 | 3.20 |
| W1010 | 78 | 19.21 | 691.70 | 71.64 | 14.33 | 54.20 | 5.90 | 9.30 | 11.50 | 17.70 |
| W1020 | 82 | 10.24 | 368.81 | 55.76 | 11.15 | 25.94 | 2.60 | 4.00 | 4.90 | 7.60 |
| W1130 | 80 | 8.68 | 312.59 | 63.50 | 12.70 | 22.22 | 1.50 | 2.40 | 3.10 | 5.00 |
| W1180 | 70 | 28.22 | 1015.91 | 108.86 | 21.77 | 60.38 | 1.70 | 3.20 | 4.40 | 7.80 |
| Total | 565.02 | 34.20 | 51.20 | 62.10 | 92.30 | |||||
Determinación de las zonas de inundación por periodo de retorno
Los peligros de inundación en zonas áridas y semiáridas son poco entendidos debido a la falta de información acerca de su comportamiento hidrológico e hidráulico, e inciden en la vulnerabilidad de la infraestructura ubicada en las llanuras de inundación. Así, este tipo de análisis es necesario para ubicar las zonas expuestas a riesgos por escorrentía asociadas con inundaciones repentinas. En el caso del cauce del Río Nuevo, tales zonas se definieron al usar el acoplamiento del modelo hidrológico e hidráulico, como se presenta a continuación.
Las profundidades y al área de inundación para los diferentes periodos de retorno analizados se muestran en la Tabla 7, donde se observa que durante el periodo de retorno de 500 años, el rango de profundidad alcanzó hasta los 6.0 metros y una superficie inundable de 237.83 ha; mientras que en el de 20 años, la profundidad alcanzó 4.80 metros y un área de 190.55 ha.
Tabla 7 Áreas de inundación y profundidades para cada periodo de retorno analizado.
| Periodo de retorno | Área de inundación (ha) | Rango de profundidad (m) |
|---|---|---|
| 20 | 190.55 | 0.10 - 4.80 |
| 50 | 206.25 | 0.10 - 5.20 |
| 100 | 216.66 | 0.10 - 5.50 |
| 500 | 237.83 | 0.10 - 6.00 |
En las siguientes figuras se muestra la representación de la zona inundable para los periodos de retorno de 20 y 500 años, mismas que muestran las profundidades mínimas y máximas obtenidas en este estudio (Figura 5).

Figura 5 Extensión de la inundación y distribución de profundidad generada por HEC-RAS para eventos con periodos de retorno de 20 y 500 años.
Por su parte, en la Figura 6, Figura 7, Figura 8, Figura 9 y Figura 10 se presenta la simulación hidráulica en cinco sitios de importancia sobre el cauce del Río Nuevo por medio de las secciones transversales (RS): 1 520.513, 3 360.577, 4 581.119, 8 292.628 y 9 334.141. Cabe mencionar que a partir del periodo de retorno de 20 años hasta el de 500 se observó un comportamiento similar con variaciones en la profundidad de las zonas inundadas debido a que se identifica que el cauce está definido por pendientes pronunciadas en las márgenes este y oeste.

Figura 6 Zonas inundables correspondientes a la sección 1 520.513, con afectaciones a infraestructura comercial y urbana.

Figura 7 Zonas inundables en la sección 3 360.577, con afectaciones urbanas (edificios públicos e instalaciones deportivas).

Figura 8 Zonas inundables de la sección 4 581.119, con afectaciones en asentamientos humanos e infraestructura educativa (asentamientos humanos con unas 200 familias).

Figura 9 Zonas inundables correspondientes a la sección 8 292.628, con afectaciones en infraestructura educativa.
Conclusiones
El apoyo de un ARF con enfoque en los L-momentos permite alimentar un modelo hidrológico e hidráulico en una zona con pocas estaciones climatológicas y registros históricos de información. Además, es una herramienta útil en el procesamiento de datos y permite dar mayor certeza al identificar los cuantiles de los periodos de retorno y estimar la altura de la precipitación, misma que será utilizada como la base del modelo hidrológico. Cabe mencionar que el manejo de la información del SIG mediante las extensiones HEC-GeoRAS y HEC-GeoHMS permitió llevar a cabo la preparación de los datos de entrada para el acoplamiento del modelo hidrológico HEC-HMS con el modelo hidráulico en HEC-RAS. El resultado de este acoplamiento de modelos en la región semiárida de la cuenca transfronteriza del Río Nuevo es relevante por ser la primera vez que se realiza y, por lo tanto, se espera que sea la base para futuros análisis hidrológicos e hidráulicos de la zona.
El acelerado crecimiento de la ciudad es condicionante en el incremento de sitios impermeables de la zona urbana y del volumen de descarga de la escorrentía. Por lo cual, se recomienda evaluar y ajustar periódicamente el CN por microcuenca, según la metodología propuesta en este trabajo, con especial atención en las zonas aledañas a los escurrimientos principales dentro del núcleo urbano.
Si bien es cierto que el aumento en la magnitud de la precipitación en los periodos de retorno de 20, 50, 100 y 500 años generaron aumentos en el volumen de descarga, el área de inundación no se incrementó de modo significativo debido a que el cauce principal del Río Nuevo se encuentra definido por taludes pronunciados en sus márgenes este y oeste. Por lo tanto, la amenaza más importante identificada en un evento extremo de precipitación se relaciona con la profundidad del agua, que alcanza alturas de 4.80 m para el TR de 20 años hasta 6.0 metros en un TR de 500 años. Cabe mencionar que el incremento de profundidad durante estos eventos representa una amenaza, pues en el área se ha desarrollado infraestructura vial, asentamientos humanos, edificios públicos y privados que albergan actividades de gobierno, y centros educativos. Otra afectación inmediata se presenta en las vialidades que conectan la ciudad de este a oeste, y que intersectan con el Río Nuevo, pues se observó en los mapas de inundación una discontinuidad vial que divide a la ciudad en dos partes, dificultando la comunicación. Este fenómeno se presenta en cualquiera de los cuatro periodos de retorno analizados. Por otro lado, se propone llevar a cabo este análisis por microcuenca, para establecer el nivel de encharcamiento e inundación en diferentes partes de la ciudad.
Además, se propone analizar el comportamiento hidráulico del embovedado del Río Nuevo, integrándolo como parte de las variables de entrada del modelo, para optimizar los resultados obtenidos en HEC-RAS.
Por último, los resultados de esta investigación podrán ser utilizados por los planeadores urbanos, autoridades municipales, estatales, federales, sistemas de protección civil y la sociedad en general, a fin de planificar acciones que den soluciones integrales a la gestión de los riesgos asociados con inundaciones súbitas.











 texto en
texto en