Modelo esfuerzo-deformación para elementos de concretos reforzado que cumple con las hipótesis de las NTC RCDF 2004

 

Edgar I. Villagrán A., César Vera M., Ana Elena Posada S.

 

 

¹ Facultad de Ingeniería, Benemérita Universidad Autónoma de Puebla, BUAP. Edificio 108-C, Ciudad Universitaria, Blvd. Valsequillo Esq. Av. San Claudio S/N, Col. San Manuel, C.P. 72570 Puebla, Puebla, México. E-mail: edgar_villagran@hotmail.com; bustamante.vera@gmail.com; anaelena.posada@correo.buap.mx.

 

Recibido el 24 de julio de 2013
Aprobado el 24 de octubre de 2013

 

Resumen

Se propone un modelo para la relación esfuerzo-deformación para la zona comprimida de elementos de concreto reforzado que cumple formalmente con las hipótesis de diseño adoptadas en las Normas Técnicas Complementarias del Reglamento de Construcciones para el Distrito Federal 2004. Para verificar la validez del modelo propuesto se analizó, mediante la relación momento-curvatura, la resistencia, la profundidad del eje neutro y la inercia efectiva de la sección. Para fines prácticos, el modelo propuesto proporciona resultados razonables al compararlo con otros modelos conocidos.

Palabras clave: Flexión, momento - curvatura, rigidez, fluencia, eje neutro, momento de inercia.

 

Abstract

This paper a model for the relationship between strengths and strains for the compressed zone of elements of reinforced concrete that complies formally with the designs adapted by the NTC DF 2004. In order to verify the validity of the proposed model, the resistance, the depth of the neutral axis and the effective inertia of the section were analyzed. For practical purposes, the proposed model gives reasonable results when compared to other known models.

Keywords: Bending, curvature - moment, stiffness, yelding, neutral axis, inertia.

 

Resumo

Propõe-se um modelo para a relação esforço-deformação para a zona comprimida de elementos de concreto reforçados que cumpre formalmente com as hipóteses de desenho adotadas nas Normas Técnicas Complementares do Regulamento de Construções para o Distrito Federal, 2004. Para verificar a validade do modelo proposto, analisou-se, mediante a relação momento-curvatura, a resistência, a profundidade do eixo neutro e a inércia efetiva da seção. Para fins práticos, o modelo proposto proporciona resultados razoáveis quando comparado com outros modelos conhecidos.

Palavras-chave: Flexão, momento - curvatura, rigidez, fluência, eixo neutro, momentos de inércia.

 

1. INTRODUCCIÓN

Las Normas Técnicas Complementarias del Reglamento de Construcciones para el Distrito Federal 2004 (NTC RCDF) para el Diseño y Construcción de Estructuras de Concreto Reforzado, en su apartado referente al cálculo de deformaciones (segundo estado límite) en elementos sujetos a flexión, indica que la rigidez geométrica (momento de inercia) del elemento se debe considerar como uno de los siguientes dos valores: el momento de inercia agrietado (I_ag) o el momento de inercia equivalente (I_c), no obstante, el inciso 3.2.1.1 permite el empleo de un análisis más racional. En este sentido se plantea como alternativa emplear la rigidez que se obtiene a partir de la gráfica momento-curvatura, sin embargo, la norma no recomienda ningún modelo esfuerzo-deformación para el cálculo de esta gráfica.

De acuerdo con la teoría de elementos de concreto reforzado sujetos a flexión, el momento actuante My la curvatura de la sección Ф están relacionados por la expresión [1]:

 

donde I_ef es el momento de inercia efectivo de la sección, E_c el módulo de elasticidad del concreto, M el momento flexionante y la curvatura de la sección. Considerando que la expresión [1] es válida hasta la falla del elemento, se puede determinar el momento de inercia efectivo de la sección para cualquier valor del momento actuante por la siguiente expresión:

Como se observa de la expresión [2], el momento de inercia es una cantidad variable que depende del momento actuante y de la curvatura de la sección, de aquí la importancia de conocer la relación momento-curvatura.

El momento actuante M, se determina a través de los esfuerzos internos que se desarrollan en la zona comprimida del concreto y en el acero. En el acero, debido al diámetro relativamente pequeño, los esfuerzos se distribuyen uniformemente en la sección y se supone una relación lineal entre esfuerzos y deformaciones hasta la fluencia del material y a partir de ese punto los esfuerzos permanecen constantes. En cuanto al concreto, el problema es mucho más complejo ya que, hasta la actualidad, no se conoce ningún modelo exacto que represente la relación esfuerzo-deformación en la zona comprimida del concreto, aunque se conocen varios modelos aproximados como son los modelos de E. Hognestad y de C. Todeschini que más adelante se mencionan.

El objetivo de este trabajo es proponer un modelo aproximado de la relación esfuerzo-deformación válido para la zona de compresión del concreto reforzado que sea congruente con las hipótesis de diseño adoptadas en las NTC RCDF en el sentido de que, al momento de la falla de la sección, el coeficiente β₁ sea igual a 0.85 y que el esfuerzo en la fibra externa del concreto sea igual a la resistencia máxima del concreto a la compresión, f"_c.

 

2. MODELO ESFUERZO-DEFORMACIÓN DEL CONCRETO

Para determinar la relación momento-curvatura (M-Ф) en una sección de un elemento de concreto reforzado es necesario conocer previamente la relación esfuerzo-deformación unitaria (f_c — ε_c) del concreto en la zona comprimida. Desde hace muchos años se han efectuado investigaciones muy profundas sobre la naturaleza de esta relación esfuerzo-deformación sin que hasta la fecha se conozca un modelo exacto. Sin embargo, los experimentos de E. Hognestad, et al. (1955) han mostrado que esa relación es curvilínea hasta el punto cuando el concreto alcanza su máxima resistencia y en adelante, con el aumento de las deformaciones, los esfuerzos en el concreto disminuyen hasta que ocurre la falla.

 

a) Modelo de Hognestad

Con base en investigaciones experimentales, E. Hognestad et al. (1955) propusieron el modelo esfuerzo-deformación del concreto en compresión que se muestra en la Fg. 1a. Este modelo está compuesto de una parte curvilínea descrita por una parábola que comienza en cero y termina cuando el concreto a compresión alcanza la resistencia máxima f'_c , en este punto la parábola es tangente a la horizontal. A partir de este punto los esfuerzos del concreto disminuyen linealmente conforme aumentan las deformaciones hasta que ocurre la falla. La expresión que representa este modelo es:

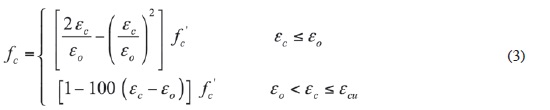
donde f_c y ε_c es el esfuerzo y la deformación unitaria en el concreto, respectivamente, mientras que es la deformación unitaria correspondiente a f'_c y ε_cu es la deformación unitaria máxima útil del concreto en compresión.

 

b) Modelo de Todeschini

Todeschini et al. (1964) propusieron que el modelo esfuerzo-deformación se puede representar por una sola parábola (Fig. 1b) cuya ecuación es:

Para fines prácticos, en algunos casos se considera que la resistencia máxima f'_c se alcanza para una deformación del concreto ε₀ = 0.002 [1] y que el concreto falla cuando ε_cu = 0.003; sin embargo, estos valores no se deben tomar como definitivos.

 

c) Modelo propuesto

En las hipótesis de las NTC RCDF se acepta que en el momento de la falla del concreto (ε_c = ε_cu en la fibra comprimida externa) el bloque curvilíneo de esfuerzos se sustituya por otro rectangular equivalente que tenga un esfuerzo f"_c constante y una profundidad a igual con β₁c (Fig. 2), donde c es la profundidad del eje neutro y β₁ es un coeficiente igual a:

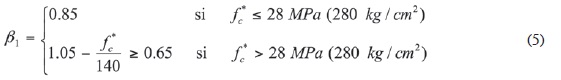
En estas normas se considera que f"_c = 0.85 f*_c y f*_c= 0.8 f'_c, donde f'_c es la resistencia nominal del concreto. Entonces, de acuerdo con las NTC RCDF, en el momento de la falla se debe cumplir que los esfuerzos en el concreto sean igual a f"_c y β₁= 0.85 para concretos con f*_c ≤ 28 MPa (280 kg / cm²).

Si bien es cierto que empleando el modelo de esfuerzos propuesto por Hognestad o el de Todeschini se obtiene que β₁ es igual con 0.85; sin embargo, con estos modelos no se cumple la hipótesis de que al momento de la falla, los esfuerzos en el concreto sean igual con f"_c (Fig. 2).

En el reglamento del CEB se elimina esta última inconsistencia considerando que para deformaciones mayores que ε_o, los esfuerzos en el concreto se mantienen constantes e igual a f'_c (Fig. 1c). Sin embargo, esta corrección tiene como consecuencia que el coeficiente β₁ no sea igual a 0.85, si se considera que se mantienen las otras condiciones.

Con la finalidad de que el modelo esfuerzo-deformación cumpla y sea congruente con las hipótesis aceptadas en las normas NTC RCDF, en este trabajo se propone modificar el modelo de Hognestad de la siguiente manera (Fig. 3): en primer lugar, la parte curvilínea alcanza el esfuerzo f"_c cuando la deformación en el concreto es de ε_o= 0.00135, y en segundo lugar, a partir de este punto se considera que los esfuerzos en el concreto se mantienen constantes hasta la falla. Este modelo queda representado por la expresión:

Con ε_o= 0.00135 y ε_cu = 0.003.

En la Fig. 4 se comparan gráficamente los modelos de la relación esfuerzo-deformación expresados por las fórmulas [3], [4] y [6]. En la figura se observa que el modelo propuesto cumple formalmente con las hipótesis de las NTC RCDF aunque predice esfuerzos mayores que los otros dos.

Con el objetivo de comprobar la pertinencia del modelo propuesto en este trabajo, en la sección 3 se hace un análisis y se compara con los modelos de Hognestad y el de Todeschini a través de la gráfica momento-curvatura.

 

3. ANÁLISIS DEL MODELO ESFUERZO-DEFORMACIÓN PROPUESTO

Para comprobar la congruencia del modelo esfuerzo-deformación propuesto con las hipótesis de las NTC RCDF, se calculó el coeficiente β₁ del bloque equivalente de esfuerzos, considerando que la fuerza de compresión calculada mediante el modelo esfuerzo-deformación propuesto debe ser igual a la calculada con el bloque equivalente de esfuerzos.

Es decir:

Despejando de esta última expresión β₁, se obtiene:

El procedimiento de cálculo del coeficiente β₁ es similar al cálculo de la gráfica momento-curvatura [6]. En la Fig. 5 se muestra la gráfica del coeficiente β₁ como una función de las deformaciones unitarias del concreto ε_c utilizando los modelos de esfuerzo-deformación expresados por las fórmulas [3], [4] y [6]. Como se observa, en general las curvas no coinciden pero todos los modelos dan el mismo valor de β₁ = 0.85 para ε_cu = 0.003, como lo indican las normas.

Un aspecto relevante es conocer el efecto que tiene el modelo propuesto en la relación momento-curvatura. Como se puede apreciar en la Fig. 6a, la gráfica momento-curvatura del modelo propuesto es similar a la de los modelos de Hognestad y Todeschini, sin embargo, el modelo propuesto proporciona momentos resistentes más grandes. En la Fig. 6b se graficó la relación entre el momento resistente calculado con el modelo propuesto y el de Todeschini y el calculado con el modelo de Hognestad. En esta gráfica se aprecia que para curvaturas muy pequeñas, los momentos resistentes del modelo propuesto son mayores, aproximadamente en un 30 % que los calculados con el modelo de Hognestad. También se observa que en la vecindad y después de la fluencia del acero, los momentos del modelo propuesto son mayores que los del modelo de Hognestad en un porcentaje que va aproximadamente del 8 % al 1 %.

Es importante observar que de acuerdo con el modelo esfuerzo-deformación propuesto, el concreto puede experimentar deformaciones mayores de ε_o sin que falle pero los esfuerzos en él ya no se modifican. Sin embargo, las deformaciones en el acero de tensión crecen acompañadas de un aumento en los esfuerzos hasta que el acero fluye. Cuando esto último ocurre, en la sección actúa el momento máximo o momento resistente M_R. En el caso analizado, el momento resistente también se puede determinar por la expresión 2.4 de las NTCR RCDF que se obtiene a partir del bloque equivalente de esfuerzos [1]:

Como se comprobó, el momento resistente determinado por la gráfica momento-curvatura prácticamente coincide con el calculado mediante la fórmula [9].

Otro parámetro que se puede analizar es el de la profundidad del eje neutro c. Como consecuencia de que el modelo esfuerzo-deformación propuesto proporciona esfuerzos mayores para una misma deformación del concreto ε_c, la fuerza de compresión aumenta y por lo tanto también debe aumentar la fuerza de tensión para que se mantenga el equilibrio. Lo anterior provoca que las deformaciones en el acero de tensión aumenten pero como consecuencia de la disminución de la profundidad del eje neutro. En la Fig. 7a se muestra la variación de la profundidad del eje neutro c, como una función de las deformaciones de la fibra externa de la zona comprimida del concreto, para los mismos datos de las figuras anteriores. Se aprecia claramente que el modelo propuesto arroja valores de c menores que los otros dos modelos. En la Fig. 7b se graficó la relación de la profundidad del eje neutro calculada con el modelo propuesto y con el de Hognestad. Se observa que en la zona de interés práctico el modelo propuesto arroja valores de c menores en 5-12 % que el modelo de Hognestad.

Finalmente, también es importante conocer como afecta el modelo propuesto al momento de inercia efectivo de la sección. Al principio de este trabajo se mencionó que el momento de inercia efectivo se determina mediante la relación momento-curvatura, es decir, para cada valor de la deformación ε_c se conocen los valores correspondientes del momento y la curvatura de la sección, entonces el valor del momento de inercia efectivo se determina aplicando la ecuación [2].

En la Fig. 8a se muestra el comportamiento del momento de inercia efectivo en función del momento actuante y del modelo de esfuerzo-deformación adoptado. Como se observa, el modelo propuesto arroja valores del momento de inercia efectivo mayores que los otros dos modelos; sin embargo, en la zona cercana al momento resistente la diferencia es pequeña. En la Fig. 8b se presenta la relación entre el momento de inercia efectivo calculado utilizando el modelo propuesto y el de Todeschini con el de Hognestad. Se observa en esta figura, que en la zona de interés práctico el modelo propuesto proporciona inercias del orden de un 5 % mayor que el de Hognestad.

En la Fig. 9a se muestra la gráfica del momento de inercia efectivo, calculado con el modelo esfuerzo-deformación propuesto, para varias cuantías de acero de refuerzo. Se observa que el acero de refuerzo a tensión no solo aumenta considerablemente el momento resistente, sino que además incrementa de manera importante la rigidez de la sección. En la Fig. 9b se graficó la relación entre el momento de inercia efectivo y el momento de inercia total I_g ( I_a = bh³ / 12), se observa que para porcentajes (p) bajos del acero de refuerzo, el momento de inercia efectivo es del orden del 20 % del momento de inercia total pero, para cuantías de acero de refuerzo mayores que la balanceada, la inercia efectiva puede ser mayor incluso que la inercia bruta I_g. Esto último no es exclusivo del modelo propuesto, ya que se observa en todos los modelos esfuerzo-deformación analizados.

Los resultados presentados en las figuras anteriores corresponden a un caso particular y para confirmarlos se analizaron otras secciones rectangulares con ancho de base entre 200 y 500 mm y relación de aspecto h/b de 1 a 3 para cuantías de acero entre la mínima y la balanceada, obteniéndose resultados similares. Por lo anterior, es posible afirmar que el modelo esfuerzo-deformación propuesto en este trabajo es razonable para aplicarlo con fines prácticos.

 

4. CONCLUSIONES

1) Se propone un modelo matemático de la relación esfuerzo-deformación para el concreto de la zona comprimida, que cumple formalmente con las hipótesis aceptadas por las NTC RCDF.

2) Se verificó que utilizando el modelo propuesto se obtiene prácticamente el mismo momento resistente que con el bloque equivalente de esfuerzos.

3) Para fines prácticos, los valores de la profundidad del eje neutro, del momento resistente y del momento de inercia efectivo calculados con el modelo propuesto son razonablemente similares a los obtenidos con otros modelos conocidos.

4) Empleando el modelo propuesto, es posible evaluar el momento de inercia efectivo de la sección compuesta de una forma más racional, que a través de la sección transformada agrietada.

 

REFERENCIAS

E. Hognestad, N. W. Hanson y D. McHenry. (1955), "Concrete Stress Distribution in Ultimate Strength Design", ACI Journal Proceedings, Vol. 52 No. 4, pp. 455-479.         [ Links ]

EN 1992-1-2, "Design of Concrete Structures Part 1-2", Comiteé Europeén de Normalization, Brussels, Eurocode 2 pr.         [ Links ]

Gobierno del Distrito Federal. (2004), "Normas Técnicas Complementarias para Diseño y Construcción de Estructuras de Concreto", México.         [ Links ]

Todeschini C. E., Bianchini A. B., y Kesler C. E. (1964), "Behavior of Concrete Columns Reinforced with High Strength Steels", ACI Journal Proceedings, Volume 61, pp. 701-716.         [ Links ]

Vargas M. G., González A. J. (2005), "Procedimiento para obtener gráficas momento-curvatura en vigas de concreto reforzado", Ingeniería Revista Académica, (9-1) pp. 37-47.         [ Links ]