Comparación de técnicas de estimación de volumen fustal total para cinco especies de pino de Durango, México

 

Comparisons of bole volume estimation techniques for five pine species of Durango, Mexico

 

S. Corral–Rivas¹; J. de J. Návar–Cháidez^2*

 

¹ Profesor investigador, Instituto Tecnológico de El Salto, Durango, MÉXICO.

² Profesor–Investigador. CIIDIR–IPN. Calle Sigma Núm. 119 Fracc. 20 de Noviembre II. Durango, Durango. MÉXICO. C. P. 34220 Tel: 618– 8142091. Correo–e: jnavar@ipn.mx. *Autor para Correspondencia.

 

Recibido: 21 de Abril, 2008
Aceptado: 18 de Febrero, 2009

 

RESUMEN

En este estudio se compararon diez técnicas de cubicación de volumen fustal total sin corteza para cinco especies de pino en Durango, México. El volumen de cada árbol se estimó con las ecuaciones convencionales de: 1) Smalian, 2) Newton y 3) Sólidos de revolución y con los modelos de ahusamiento 4) Amidon, 5) Biging, 6) Clutter, 7) Kozak 1, 8) Kozak 2, 9) Newnham y 10) Rustagi y Loveless. Los modelos convencionales de: a) Schumacher y Hall, b) Spurr, c) Spurr transformado, d) Honer, e) Sloboda, f) Naslund y g) Australiana se ajustaron a los volúmenes estimados por las técnicas descritas con el uso de las variables independientes diámetro normal y altura total. Los modelos de volumen fueron comparados por medio de un análisis de covarianza con la finalidad de utilizar aquellos comparables con la estimación del volumen por la ecuación convencional de Smalian. Los resultados mostraron que las ecuaciones de ahusamiento de Amidon y Biging proveen volúmenes comparables al nivel del árbol o del rodal con los generados por las ecuaciones de volumen convencionales que se alimentan con el volumen estimado por la ecuación de Smalian, de Huber o de Newton. Por esta razón, los dos modelos se recomiendan para estimar los volúmenes totales y comerciales de las cinco especies de pino de Durango, México.

Palabras clave: cubicación convencional, modelos de ahusamiento, ecuaciones de volumen, fuste total sin corteza, pino, México.

 

ABSTRACT

In this study, ten methods for estimating total stem (bole) volume inside bark, were compared for five pine species distributed in the State of Durango, Mexico. Total stem volume was thus estimated by the conventional equations of 1) Smalian, 2) Newton and 3) revolution of solids, and the taper models of 4) Amidon, 5) Biging, 6) Clutter, 7) Kozak 1, 8) Kozak 2, 9) Newnham and 10) Rustagi and Loveless. Total tree stem volume models of a) Schumacher and Hall, b) Spurr, c) Spurr transformed, d) Honer, e) Sloboda, f) Naslund and g) Australian, were fitted to estimated volumes by the indicated mathematical methods using the independent variables, diameter at breast height (d) and total height. Volume data generated by those conventional models were compared using covariance analysis with the aim to employ those that are compatible with the tree volume estimation by the conventional equation of Smalian. Results showed that the taper equations of Amidon and Biging provided comparable tree and stand volumes to those estimated by the conventional approaches that employ the volume estimated by the Huber, Smalian or Newton equations. Therefore, these two taper equations are widely recommended to estimate total or merchantable volume of the five studied pine species of Durango, Mexico.

Keywords: total stem volume estimation, taper functions, volume equations, pine species, Mexico.

 

INTRODUCCIÓN

La estimación de los volúmenes fustal total y comercial de los árboles de un rodal, constituye una herramienta básica de los inventarios forestales, pues estos parámetros son muy importantes en la planeación del manejo forestal. Así pues, para la estimar el volumen de árboles individuales se han utilizado dos procedimientos: mediciones del diámetro a intervalos específicos de la altura o a través de técnicas de desplazamiento de agua de un recipiente (xilómetro), o procedimiento de Arquímides. En cualquiera de estos casos, las técnicas de medición (xilómetro) y de estimación (ecuaciones de Smalian, Huber o Newton) proveen cálculos adecuados del volumen del fuste del árbol (Biging, 1988).

Martin (1984) comparó el volumen de 243 trozas de 72 especies latifoliadas con 14 ecuaciones contra el volumen estimado por el xilómetro, encontrando que las ecuaciones convencionales de Huber, Newton y Smalian fueron iguales de precisas para estimar el volumen, seguidos muy de cerca por la ecuación de ahusamiento de Beers que el procedimiento de Arquímides.

De manera muy similar, Biging (1988) reportó que las fórmulas de Newton y Huber son las más adecuadas para estimar el volumen de árboles individuales, seguidas por la fórmula de Smalian. Así mismo, Figueiredo y Budant (1999) encontraron errores menores cuando el volumen total es estimado con las fórmulas de Smalian y Huber, en comparación con la técnica del xilómetro; también encontraron que el error obtenido fue mayor, al incorporar a los cálculos, cinco ecuaciones de ahusamiento.

Actualmente, las funciones de ahusamiento son populares y eficientes para representar el perfil del fuste de los árboles y para estimar por integración, volúmenes comerciales y totales (Clutter et al., 1983; Návar et al., 1997; Tapia y Návar, 1998; Maldonado y Návar, 2000). Los modelos de Damaerschalk (1972) y Clutter (1980) son compatibles con las ecuaciones de volumen total estimado por integración de las funciones de ahusamiento y con el volumen obtenido por ecuaciones convencionales de volumen total. Diversas funciones compatibles de ahusamiento han sido derivadas para obtener volumen total o parcial del fuste (Clutter, 1980; Reed y Green, 1984; Amidon 1984; Biging, 1984; Byrne y Reed, 1986; McTague y Bailey, 1987; Rustagi y Loveless, 1991; Bailey, 1994; Fang y Bailey, 1999). Pero existen escasas comparaciones de la estimación del volumen a nivel del rodal.

En México hay pocos trabajos que describen compatiblemente el perfil y el volumen fustal de árboles provenientes de bosques mixtos e irregulares (Návar et al., 1997; Corral et al., 1999). Así pues, aunque existe una gran variedad de funciones de ahusamiento, muchos de estos no han comparado el volumen a nivel del árbol o del rodal obtenido por integración analítica o numérica contra ecuaciones convencionales de cubicación, ni han sido aplicados extensivamente en la determinación del volumen fustal y comercial de las coníferas de la Sierra Madre Occidental en el estado de Durango.

El objetivo de este trabajo fue comparar el volumen fustal total sin corteza a nivel del árbol individual y del rodal estimado mediante diez formas de cubicación con el uso de ecuaciones convencionales de estimación de volumen fustal. La hipótesis implícitamente planteada, es que existen ecuaciones de ahusamiento cuya integración proveen las mismas estimaciones del volumen fustal y del rodal que la ecuación clásica convencional de Smalian.

 

MATERIALES Y MÉTODOS

Descripción general del área de estudio

El estudio se realizó en la región forestal de El Salto, Durango, la cual comprende los predios de la UCODEFO Núm. 6, localizándose en el sistema montañoso denominado Sierra Madre Occidental. Ésta pertenece a las Subprovincias Gran Meseta, Cañones Duranguenses y Mesetas y Cañones del Sur; se encuentra entre las coordenadas 23°30' a 24°15' de latitud norte y 105°15' a 105°45' de longitud oeste, a 100 km, al suroeste de la ciudad de Durango. Las altitudes sobre el nivel del mar fluctúan entre 1,400 y 2,600 m. La región se encuentra dentro del grupo de climas templados C, subgrupo de climas semicálidos (A)C(W₁) y tipos semicálidos subhúmedos con lluvias en verano y precipitación media anual de 800–1200 mm y una temperatura media anual de 20–22°C. La geología de la región consiste en rocas ígneas extrusivas ácidas y basaltos del cretácico superior y cretácico inferior. Las rocas son del tipo sedimentario y vulcanoso sedimentario. Los tipos de suelos encontrados son litosol, cambisol, regosol y feozem.

Por su ubicación geográfica, la zona presenta diversas condiciones de vegetación que va desde selva baja caducifolia, masas puras de encino y pino y bosque mezclado de pino–encino. Las especies de mayor valor comercial, tanto por las características tecnológicas de su madera como por su rango de distribución son las del género Pinus. Las especies listadas en orden de importancia por su volumen de aprovechamiento son: Pinus cooperi Blanco, P. durangensis Martínez, P. leiophylla Schl et Cham, P engelmanniiCarr, P. cooperivar Ornelasi, P. teocote et Cham, P. herrerae Martínez. Otras especies de menor valor comercial, distribución y abundancia son P. ayacahuite Ehrenb, P. lumholtzii Rob et Fern, P. douglasiana Martínez, P. michoacana cornuta Martínez, P. oocarpa Schiede. Además se aprovechan algunas especies de encino (Quercus spp) y otras especies asociadas con las coníferas y hojosas de los géneros Arbutus, Juniperus, Pseudotsuga, Abies y Picea.

 

METODOLOGÍA

Las mediciones del diámetro sin corteza a diferentes secciones de la altura, se realizaron directamente en árboles derribados en operaciones de aprovechamiento desde abril a octubre de 1996. Los árboles muestra fueron distribuidos en toda el área de estudio tratando de cubrir todas las calidades de sitio presentes, así como todas las categorías de diámetro y altura. El tamaño de la muestra por especie fue de 507 árboles para Pinus cooperi, 453 para P. durangensis, 424 para P. engelmannii 400 para P. leiophylla y 322 para P. herrerae. De éstos, el 75 % de cada especie se seleccionó y separó aleatoriamente para el ajuste estadístico de parámetros de los modelos de volumen y, el 25 % restante, para su validación (Cuadro 1). El diámetro sin corteza se midió a la base del fuste, a 0.30 m, a 1.30 m y, desde aquí hasta la parte distal, a cada metro. Otras variables medidas fueron: diámetro normal, edad, altura del tocón, grosor de corteza y altura total.

La cubicación de las trozas de los árboles derribados se realizó con las ecuaciones convencionales de Smalian, Newton y sólidos de revolución, para todas las secciones del fuste, con excepción de la parte distal a la cual se le aplicó la ecuación del cono.

Las ecuaciones convencionales están descritas por:

1. Smalian (1804).

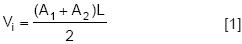
2. Newton (1849).

3. Sólidos de revolución.

Donde: V es el volumen de la troza i (m³); A₁, A₂, y A₃, son el área basal al inicio, final y promedio de la troza respectivamente (m²); R y r son los radios promedio, al inicio y final de la troza (m); L es la longitud de la troza (m); λ=0.0003141593 y N son los tipos dendrométricos (0: para el cilindro, 1: para el paraboloide, 2: para el cono y 3:para el neiloide).

Los modelos de ahusamiento utilizados para estimar el volumen fustal de las cinco especies fueron: 1) Amidon (1984); 2) Biging (1984); 3) Clutter (1980); 4) Kozak (1988) en forma no lineal 5) Kozak (1988) en forma lineal; 6) Newnham (1992) y 7) Rustagi y Loveless (1991).

Las funciones de ahusamiento polinomiales de Kozak et al. (1969), y Kozak et al. (1969) se describen en los modelos [4] y [5], respectivamente:

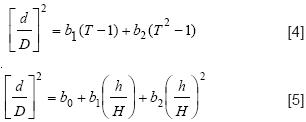
El modelo de potencia que estima el perfil del fuste de Clutter (1980) se describe por el modelo [6]

La ecuación de ahusamiento del exponente variable de Newnham (1992) es el modelo [7]:

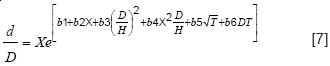
Las ecuaciones de ahusamiento de Amidon (1984) y Bigging (1984) se representan por las ecuaciones [8] y [9], respectivamente:

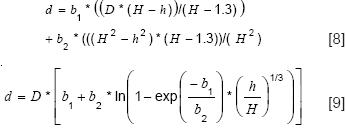
El modelo que describe el perfil del fuste de Rustagi y Loveless (1991) se presenta en [10]:

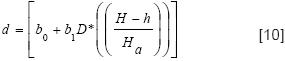
Donde: z = ((H–hi)/H); y = 2z (3*(z²)–2z)+(4*(z³)–2z) + (5*(z⁴)–2z) (6*(z⁵)–2z); x=(h–hi)/(h–1.3); x1=(d/h); x2=(d/h)²; t=(hi/h), t2=(hi/h)², t11=(t–1), t21=(t2–1), t5=Ö(t).

Descripción más detallada de la estructura de las ecuaciones son reportadas en Navar et al. (1997). El volumen se estimó por medio de integración numérica para todos los modelos de ahusamiento (Cuadro 2), con excepción de Amidon (1984) y Biging (1984) los cuales fueron integrados analíticamente. El diámetro se estimó a cada centímetro de la altura relativa del fuste hasta alcanzar la parte distal.

Los volúmenes totales estimados por las 10 técnicas descritas anteriormente fueron ajustados a siete ecuaciones convencionales de estimación de volumen con el uso de las variables independientes diámetro normal (Dn) y altura total (Ht). Las ecuaciones se describen a continuación:

1. Schumacher y Hall (1933).

2. Spurr (1952) en forma logarítmica.

3. Spurr (1952) en forma aritmética.

4. Honer (1964).

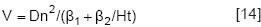
5. Sloboda de tres parámetros.

6. Naslund modificado.

7. Australiano

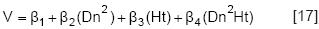
Donde: V= Volumen total del fuste; estimado por 10 diferentes técnicas Dn= Diámetro normal; Ht= Altura total; β₁...₄= coeficientes de regresión y Ln= logaritmo natural.

Los modelos con mejor ajuste fueron Schumacher y Hall y Spurr en forma logarítmica porque presentaron los coeficientes de determinación más altos, los errores estándares más bajos y errores distribuidos normalmente. Los modelos de volumen resultantes fueron comparados a través de un análisis de covarianza, donde el Ln(Dn²Ht) y Dn y Ht fueron las variables para los modelos de Spurr transformado y Schumacher y Hall, respectivamente. Este procedimiento estadístico comparó los parámetros, interceptada y pendiente de cada uno de los modelos para definir la consistencia en el cálculo del volumen por las diez diferentes técnicas de cubicación. Es decir, las ecuaciones proveen parámetros estadísticos que describen las características de la muestra en su conjunto y que pueden ser comparables para saber si son estadísticamente iguales o diferentes.

Los errores se han estimado convencionalmente de la diferencia entre el volumen observado (generalmente medido por desplazamiento de agua) y el volumen estimado por una técnica de cubicación (Martin, 1984). En este estudio se utilizó el volumen estimado por Smalian como el testigo porque diversos estudios no han encontrado diferencias significativas entre esta técnica de medición y el volumen observado por desplazamiento de agua (Martin, 1984; Reed y Green, 1984; Biging, 1988; Figueiredo y Budant, 1999).

Los errores fueron estimados a nivel del rodal y por categoría diamétrica. Con los datos del inventario forestal levantado en 1996 para el área de estudio. Se desarrolló un rodal tipo cuyas estructuras diamétricas por especie fueron predichas por la distribución Weibull y los errores totales para cada especie se estimaron con el modelo [El número de árboles y volumen por hectárea para cada especie fue estimado usando sitios de un décimo de hectárea]. El ajuste de la distribución Weibull se realizó al nivel de las especies considerando su distribución en todas las condiciones de sitio posibles en el área de estudio y los parámetros se estimaron con el procedimiento de máxima verosimilitud.

La estructura del error total fue determinada por:

Donde: E_total= Error total (%); f(x_i)= frecuencia relativa del número de árboles en la categoría diamétrica i; E= Error promedio por categoría diamétrica; N= Número de árboles promedio por hectárea y Vh= Volumen promedio por hectárea de las especies.

 

RESULTADOS

Los estadísticos promedio de ajuste y validación de las siete funciones de volumen mostraron diferencias significativas para predecir el volumen de las cinco especies estudiadas. El modelo de Schumacher y Hall (1933) mostró el mayor coeficiente de determinación y menor error estándar, seguido muy de cerca por el modelo de Spurr transformado en forma logarítmica (Cuadro 3). El modelo de Honer presentó el menor coeficiente de determinación y el mayor error estándar.

Los coeficientes de variación de los modelos para predecir el volumen fustal total oscilan del 15 hasta el 25 % para cada especie estudiada. Los errores se concentraron al origen, resultando una distribución con un alto valor de Curtosis, alejado de la distribución normal, motivo por el cual fue rechazada la hipótesis de normalidad con probabilidad menor de 0.05 (Pr<0.05). De acuerdo con los estadísticos del Cuadro 3 se recomiendan los modelos de Schumacher y Hall (1933) y Spurr (1952) transformado para predecir el volumen fustal total sin corteza de las cinco especies estudiadas.

Considerando el modelo Schumacher y Hall, el análisis de covarianza mostró, que la pendiente del diámetro normal (β₂) fue estadísticamente igual (Pr>0.05) para los modelos convencionales de cubicación (Smalian, Newton y Sólidos Geométricos de Revolución) y los modelos de Biging y Amidon para las cuatro especies, excepto para Pinus cooperi. La pendiente de la variable altura total (β₃) fue también estadísticamente igual (Pr>0.05) entre los modelos convencionales y los modelos de Amidon en P. cooperi, P engelmannii, P. leiophylla, Biging en P. durangensis y P herrerae (Figura 1a). Si se considera el modelo de Spurr, la pendiente de los modelos de cubicación convencionales (b₂) (Sólidos Geométricos de Revolución, Smalian y Newton) fue estadísticamente igual a la pendiente (β₂) de los modelos de ahusamiento de Biging y Amidon (Pr>0.05) para las especies P. engelmannii, P. leiophylla y P. herrerae, pero no para las especies P. cooperi y P. durangensis (Figura 1b).

El volumen se subestima cuando se calcula con los modelos de ahusamiento con respecto al volumen estimado por las técnicas convencionales de cubicación (Figura 1). Este error es mayor a medida que incrementan las dimensiones de los árboles y, se aproximan al cero absoluto, para árboles con diámetro normal menor a 30 cm. Sin embargo, la probabilidad calculada con la distribución Weibull de encontrar árboles de diámetros mayores a 50 cm es sólo de 10 %.

La variación en la estimación del volumen fustal sin corteza de los modelos de Amidon y Biging, en contraste con los volúmenes estimados por la ecuación convencional de Smalian, fue diferente para las especies estudiadas, representados por las funciones de Schumacher y Hall y Spurr. El volumen fustal sin corteza de Pinus cooperi estimado por los modelos de Amidon y Biging presentó un error total porcentual en volumen por hectárea de 9.1, cuando se predice con la función de Schumacher y Hall, mientras que con el modelo de Spurr fue 40.7 para ambos sistemas de cubicación. Para P. durangensis los errores totales porcentuales fueron 11.3 y 25.3 estimados con Amidon y Biging respectivamente, usando la función de Schumacher y Hall, mientras que con la función de Spurr, los errores fueron 54.3 y 85.0 respectivamente. Para P. engelmannii los errores totales porcentuales fueron 33.1 y 14.6; 76.2 y 69.4 del volumen estimado con los modelos de Amidon y Biging y predichos con las funciones de Schumacher y Hall y Spurr, respectivamente. En P. leiophylla los errores totales porcentuales fueron 17.9 y 1.4; 50.3 41.7 para los mismos modelos de ahusamiento y funciones de volumen respectivamente. Finalmente en P. herrerae los errores totales porcentuales fueron 13.3 y 3.4; 35.1 y 33.4; para el volumen estimado con Amidon y Biging y predicho con la función de Schumacher y Hall y Spurr (Cuadro 4).

De los resultados anteriores se puede observar una amplia diferencia en los errores presentados con las funciones de Schumacher y Hall y Spurr en forma logarítmica en el volumen estimado con Amidon y Biging, en contraste con el volumen estimado por Smalian. Este comportamiento se debe, parcialmente, a los errores mayores en la estimación del volumen por el modelo de Spurr transformado.

Los modelos de ahusamiento de Amidon y Biging también presentaron diferencias en estimar volumen entre las especies, excepto para Pinus cooperi donde el error porcentual fue similar. Para P. durangensis el menor error porcentual fue observado cuando el volumen se estima con la ecuación de Amidon. Para P. engelmanni, P. leiophylla y P. herrerae los menores errores se presentaron cuando el volumen se estimó con la ecuación de Biging, aunque las dos últimas especies también presentaron errores aceptables con la ecuación de Amidon.

Los modelos de Biging y Amidon pueden ser utilizados preliminarmente en la estimación de los volúmenes fustales totales y comerciales sin corteza de las especies incluidas en el estudio, porque el error para estimar volumen fustal por hectárea es bajo y cae dentro del error de la función matemática de Schumacher y Hall (Cuadro 5). No se recomienda la estimación del volumen por medio de estos modelos de ahusamiento con el uso de otras ecuaciones de volumen (Spurr transformado, Honer, Australiana, et.) por su error tan alto en la estimación del volumen fustal al nivel del rodal.

Los parámetros ajustados a los perfiles fustales con las ecuaciones de Amidon y Biging para las especies estudiadas se presentan en el (Cuadro 6).

 

DISCUSIÓN

La ecuación de Schumacher y Hall (1933) ha sido ampliamente recomendada en la estimación de componentes de volumen por numerosos investigadores de la biometría forestal (Bailey, 1994; Návar y Domínguez, 1997; Contreras–Aviña y Návar, 2002). El modelo transformado de Spurr (1952) es también utilizado para estimar el volumen del árbol de varias especies (Eljatib, 2002; Salas et al., 2005). Estos modelos se ajustan generalmente de acuerdo a la siguiente forma matemática; Ln(V) = a + b1Ln(Dn) + b2Ln(Ht) o Ln(V) = a + b1Ln(Dn²Ht). La transformación logarítmica en la estimación de parámetros estadísticos resuelve el problema de heteroscedasticidad (varianza heterogénea) y poseen menor variación estadística. Los errores absolutos (en porcentaje del volumen del fuste en m³) se estiman generalmente utilizando la ecuación siguiente V = aDn^b1Ht^b2 o V = a(Dn²Ht)^b1. En este estudio, los errores oscilaron entre 16 y 24 % del volumen promedio registrado. En otros estudios biométricos, los errores van de 15 hasta cerca del 30 % (Montalvo–Guerrero et al., 2001; Contreras y Návar, 2002; Eljatib, 2002). En contraste, otros investigadores generalmente reportan el error con dimensiones logarítmicas, el cual no es interpretable ni contrastable con otros errores (Montalvo–Guerrero et al., 2001).

El error de la ecuación de volumen derivado de la estimación de los parámetros estadísticos es tan grande como la diferencia en la estimación del volumen al nivel del rodal por el procedimiento convencional de Smalian y de la integración de la ecuación de Amidon (1984) o de Biging (1984), cuando se usa la ecuación de Schumacher y Hall (1933). En contraste cuando se emplea la ecuación transformada de Spurr (1952), la diferencia en la estimación del volumen al nivel del rodal es sobre tres veces mayor que el error en la estimación de la ecuación misma. Esta diferencia tan grande hace que el uso de la ecuación de Spurr (1952) o de cualquier otra ecuación de volumen, con la excepción de la ecuación de Schumacher y Hall (1933), cuando se alimentan con volúmenes estimados por la integración de ecuaciones de ahusamiento, sean limitadas en su aplicación en campo. Los sesgos se encuentran generalmente en la estimación de volúmenes de árboles con diámetros mayores de 40 cm y cuando se emplea una ecuación de incluyen las dos variables aleatorias independientemente (Dn y Ht), como en el modelo de Schumacher y Hall (1933), los volúmenes son estimados con menor sesgo en contraste a cuando son estimados con la ecuación típica de Smalian.

 

CONCLUSIONES

Los modelos de ahusamiento de Amidon (1984) y Biging (1984) estiman volúmenes fustales de árboles individuales y por hectárea consistentes con la ecuación convencional de Smalian, cuando se emplea la ecuación clásica de Schumacher y Hall (1933) pero se sesgan marcadamente cuando se contrastan con otras ecuaciones de volumen convencionales; como por ejemplo, la ecuación transformada de Spurr (1952). Por esta razón, cuando se requieren estimaciones de volúmenes fustales totales o comerciales de árboles individuales se recomienda el uso de cualquiera de las dos ecuaciones de ahusamiento señaladas anteriormente en la estimación del volumen y la ecuación de Schumacher y Hall (1933) en la predicción de los volúmenes al nivel del rodal de los bosques templados de Durango, México.

 

LITERATURA CITADA

AMIDON, E. L. 1984. A general taper functional form to predict bole volume for five mixted conifer species in California. For. Sci. 30: 166–171.         [ Links ]

BAILEY, R. L. 1994. A compatible volume–taper model based on the Schumacher and Hall generalizad constant for factor volume equation. For. Sci.40: 303–313.         [ Links ]

BIGING, G. S. 1984. A compatible volume – taper function for Alberta trees. For. Sci. 30:1103–1117.         [ Links ]

BIGING, G. S. 1988. Estimating the accuracy of volume equations using taper equations of stem profile. Can. J. For. Res. 18: 1002–1007.         [ Links ]

BYRNE, J. C.; REED, D. D. 1986. Complex compatible taper and volume estimation systems for red and loblolly pines. For. Sci. 32: 423–443.         [ Links ]

CASTILLO–SANTIAGO, M.A. 1988. Modelo para estimación de incremento y producción maderable neta en Pinus caribea var hondurensis Barr. y Golf., de la Sabana, Oaxaca. Tesis profesional. Chapingo, México. 81 p.         [ Links ]

CLUTTER, J. L. 1980. Development of taper functions from variable–top merchantable volume equations. For. Sci. 26: 117–120.         [ Links ]

CLUTTER, J. L.; FORTSON, J. C.; PIENNAR, J. C.; BRISTER, L.V.; BAYLEY. R. L. 1983. Timber management: A quantitative approach. Wiley New York. 333 p.         [ Links ]

CONTRERAS, J. C.; NÁVAR, J. 2002. Ecuaciones aditivas para estimar componentes de volumen para Pinus teocote de Durango, México. Ciencia Forestal en México 27: 67–82.         [ Links ]

CORRAL, S.; NÁVAR J.; FERNÁNDEZ, F. 1999. Ajuste de funciones de ahusamiento a los perfiles fustales de cinco pináceas de la región de El Salto, Durango. Madera y Bosques.         [ Links ]

DAMAERSCHALK, J. P. 1972. Converting volume equations to compatible taper equations. For. Sci. 18: 241–245.         [ Links ]

DE LOS SANTOS–POSADAS, H. M.; VALDÉZ–LAZALDE, J. R.; RODRÍGUEZ–AGUILAR, M. 1995. Uso del modelo compatible volumen–ahusamiento de Bailey en dos especies de pino. II Congreso de Mexicano sobre Recursos Forestales. Resumen de ponencia. Desarrollo sustentable: redefiniendo el papel de los recursos forestales. Montecillo, México. 91 p.         [ Links ]

ELJATIB, C. S. 2002. Ajuste y validación de ecuaciones de volumen para un relicto del bosque de Roble–Laurel–Lingue. Bosque (Valdivia) 23: 81–92.         [ Links ]

FANG, Z.; BAILEY, R. L. 1999. Compatible volume and taper models with coeficients for tropical species on Hainan Island in Southern China. For. Sci. 45(1): 85–100.         [ Links ]

FIGUEIREDO, F. A.; BUDANT, S. L. 1999. Comparison between predicted volumes estimated by taper equations and true volumes obtained by the water displacement technique (xylometer). Can. J. For. Res. 29: 451–461.         [ Links ]

HONER, T. G. 1964. The use of height and squared diameter ratios for the estimation of cubic foot volume. For Chron. 40: 324–331.         [ Links ]

KOZAK, A. 1988. A variabl e–exponent taper equation. Can. J. For. Res. 18:1363–1368.         [ Links ]

MALDONADO, D.; NÁVAR, J. 2000. Ajuste de funciones de ahusamiento de cinco especies de pino en plantaciones en la región de El Salto, Durango, México. Revista Chapingo. Serie Ciencias Forestales y del Ambiente 6(2): 159–164.         [ Links ]

MARTIN, A. J. 1984. Testing volume equation accuracy with water displacement techniques. For. Sci. 30: 41–50.         [ Links ]

McTAGUE, J. P.; BAILEY, R. L. 1987. Simultaneous total and merchantable volume equations and compatible taper functions for loblolly pine. Can. J. For. Res. 17: 87–92.         [ Links ]

MONTALVO–GUERRERO, J. M.; BUENO–LÓPEZ, S.; TORRES, G. J. 2001. Ecuaciones para el calculo del volumen del árbol para Pinus occidentales SW., en el Plan Sierra, República Dominicana. Revista Chapingo. Serie Ciencias Forestales y del Ambiente 7: 49–53.         [ Links ]

NÁVAR, J.; DOMÍNGUEZ, C. P. A. 1997. Ajuste de modelos de volumen y funciones que describen el perfil diametrico de cuatro especies de pino plantadas en el nordeste de Mexico. Investigación Agraria: Sistemas Forestales: 6(1,2): 147–162.         [ Links ]

NÁVAR J.; DOMÍNGUEZ–CALLEROS, P. A.; CONTRERAS–AVIÑA, J. C.; ESTRADA M., C. 1997. Ajuste de siete modelos de ahusamiento a los perfiles fustales de Pinus hartwegii Lindl., del Noreste de México. Agrociencia 31: 73–81.         [ Links ]

NEWNHAM, R. M. 1992. Variable–form taper functions for four Alberta tree species. Can. J. For. Res. 22: 210–223.         [ Links ]

REED, D. D.; GREEN, E. J. 1984. Compatible stem taper and volume ratio equations. For. Sci. 30: 977–990.         [ Links ]

RUSTAGI, K. P.; LOVELESS, R. S. 1991. Compatible variable–form volume and stem profile equations for Douglas–fir. Can. J. For. Res. 21: 143–151.         [ Links ]

SALAS, C.; NIETO, L.; IRISARRI, A. E. 2005. Modelos de volumen para Pinus pinaster Ait. en la Comarca del Baixo Miño, Galicia, España. Quebracho 12: 11–22.         [ Links ]

SCHUMACHER, F. X.; HALL, F. S. 1933. Logarthmic expression of timber–tree volume. J. Agric. Res. 47: 719–734.         [ Links ]

SPURR, S. H. 1952. Forest inventory. John Wiley and Sons. New York. 472 p.         [ Links ]

TAPIA, J.; NÁVAR, J. 1998. Ajuste de modelos de volumen y funciones de ahusamiento para Pinus teocote en bosques de pino de la Sierra Madre Oriental. Ciencia e Investigacion Forestal 12(1): 5–19.         [ Links ]