Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Chapingo serie ciencias forestales y del ambiente
versión On-line ISSN 2007-4018versión impresa ISSN 2007-3828
Rev. Chapingo ser. cienc. for. ambient vol.25 no.1 Chapingo ene./abr. 2019 Epub 15-Feb-2021
https://doi.org/10.5154/r.rchscfa.2018.03.026
Artículo científico
Diagrama de manejo de la densidad para los bosques mezclados de la región de El Salto, Durango
1Instituto Tecnológico de El Salto, Programa de Maestría en Ciencias en Desarrollo Forestal Sustentable. Mesa del Tecnológico s/n. C. P. 34942. El Salto, Pueblo Nuevo, Durango, México.
2Instituto Nacional de Investigaciones Forestales, Agrícolas y Pecuarias (INIFAP), Campo Experimental Valle del Guadiana. km 4.5 carretera Durango-Mezquital. C. P. 34170. Durango, Durango, México.
Introducción:
Los diagramas para el manejo de la densidad (DMD) son herramientas útiles en la caracterización y manejo de la densidad del rodal.
Objetivo:
Desarrollar un DMD para programar aclareos en los bosques naturales mezclados de la región de El Salto, Durango.
Materiales y métodos:
Los datos se obtuvieron en 441 parcelas temporales de muestreo en 263 rodales mezclados con especies de los géneros Pinus y Quercus, principalmente. El DMD se basó en el índice de Hart-Becking y una relación de dos ecuaciones alométricas: 1) el diámetro medio cuadrático (dg, cm) con la densidad (N, árboles·ha-1) y altura dominante (Hd, m), y 2) el volumen (V, m3·ha-1) con el dg, Hd y N. En el ajuste de los parámetros de las ecuaciones se utilizó el método de mínimos cuadrados ordinarios no lineales en forma simultánea. El límite de densidad máxima se estimó mediante regresión cuantílica potencial que relacionó N con la Hd.
Resultados y discusión:
En los modelos ajustados se obtuvieron estadísticos de bondad de ajuste eficientes, en términos de la raíz del error medio cuadrático (2.29) y coeficiente de determinación (0.86). El DMD sugiere aplicar aclareos debajo de la línea de densidad máxima para evitar mortalidad. A través del DMD se pueden evaluar diferentes alternativas silvícolas, programar aclareos, maximizar el espacio de crecimiento, promover el incremento de árboles y mejorar los productos forestales.
Conclusión:
El DMD desarrollado es útil para programar aclareos con fines de producción de madera para asierre al final del turno.
Palabras clave: aclareo; altura dominante; densidad máxima; índice de Hart-Becking; regresión cuantílica
Introduction:
Density management diagrams (DMDs) are useful tools for characterizing and managing stand density.
Objective:
To develop a DMD to schedule thinnings in the natural mixed-species forests of the El Salto region, Durango.
Materials and methods:
The data were collected in 441 temporary sampling plots in 263 mixed-species stands with mainly species of the Pinus and Quercus genus. The DMD was based on the Hart-Becking index and a relationship of two allometric equations: 1) the quadratic mean diameter (dg, cm) with the density (N, trees·ha−1) and dominant height (Hd, m), and 2) the volume (V, m3·ha−1) with the dg, Hd and N. In fitting equations, the ordinary Nonlinear Least Squares (NLS) method was used simultaneously. The maximum density limit was estimated by potential quantile regression that related N to Hd.
Results and discussion:
Efficient goodness-of-fit statistics were reported in the fitted models, in terms of Root Mean Square Error (2.29) and coefficient of determination (0.86). The DMD suggests applying thinnings below the maximum density line to avoid mortality. Through the DMD it is possible to evaluate different silvicultural alternatives, schedule thinnings, maximize growth space, promote tree growth and improve forest products.
Conclusion:
The DMD developed is useful for thinning scheduling to obtain saw-timber at rotation age.
Keywords: thinning; dominant height; maximum density; Hart-Becking index; quantile regression
Introducción
Los árboles se consideran los elementos más importantes en un ecosistema forestal, ya que presentan características morfológicas distintas que dan lugar a estructuras diferentes en diámetro, altura y densidad. Esta última característica es muy importante para la evaluación de la competencia entre árboles de un rodal o bosque determinado (Berger & Puettmann, 2000).
La densidad es un factor que determina la productividad de un sitio forestal y puede manipularse con relativa facilidad por el manejador forestal mediante los aclareos (Daniel, Helms, & Baker, 1982). No obstante, la determinación de los niveles adecuados de densidad del rodal es un proceso complicado que depende de factores biológicos, tecnológicos y operacionales (Diéguez-Aranda et al., 2009). La densidad de una especie, mezcla de especies o región determinada se maneja mediante diferentes espesuras que contemplan límites superior e inferior para la aplicación de aclareos. Para lograr un manejo eficiente en el control de la densidad del rodal es necesario que el manejo forestal cuente con herramientas cuantitativas como los diagramas de manejo de la densidad (DMD).
Los DMD reflejan relaciones fundamentales entre el número de árboles, su tamaño, la ocupación del espacio de crecimiento y el autoaclareo (Vacchiano, Motta, Long, & Shaw, 2008). En el control de la densidad óptima del rodal se sugiere establecer un límite superior que correspondería con la densidad máxima que un rodal es capaz de sustentar en las diferentes etapas de desarrollo (Barrio-Anta, Balboa-Murias, Castedo-Dorado, Diéguez-Aranda, & Álvarez-González, 2006). Un DMD es un modelo gráfico que permite programar los aclareos en un rodal para anticipar la mortalidad de los árboles por autoaclareo; además, los efectos de las cortas se pueden simular y predecir en un tiempo determinado (Magaña-Torres, Torres-Rojo, Rodríguez-Franco, Aguirre-Díaz, & Fierros-González, 2008). También, los DMD son herramientas útiles para desarrollar, evaluar y mostrar alternativas de manejo de la densidad del rodal para propósitos que van desde la optimización del hábitat de la fauna silvestre (Sturtevant, Bissonette, & Long, 1996) hasta la producción de biomasa aérea (Castedo-Dorado, Crecente-Campo, Álvarez-Álvarez, & Barrio-Anta, 2009).
En México, los DMD se han desarrollado para bosques regulares con diferentes especies (Márquez-Linares & Álvarez-Zagoya, 1995; Santiago-García et al., 2013; Quiñonez-Barraza et al., 2018) y plantaciones comerciales de Tectona grandis L. f. (Minoche, Risio-Allione, Herrero, & Martínez-Zurimendi, 2017); sin embargo, son pocos los trabajos publicados en bosques naturales con mezcla de especies (Corral-Rivas, Álvarez-González, Corral-Rivas, Wehenkel, & López-Sánchez, 2015; Torres-Rojo & Velázquez-Martínez, 2000). Por lo anterior, el objetivo de este trabajo fue desarrollar un DMD como herramienta para la planeación y prescripción de aclareos en bosques mezclados del ejido Borbollones, Pueblo Nuevo, Durango. Además, se ilustra el uso del diagrama para un esquema de manejo, cuyo propósito es la producción de madera para asierre al final del turno.
Materiales y métodos
Área de estudio
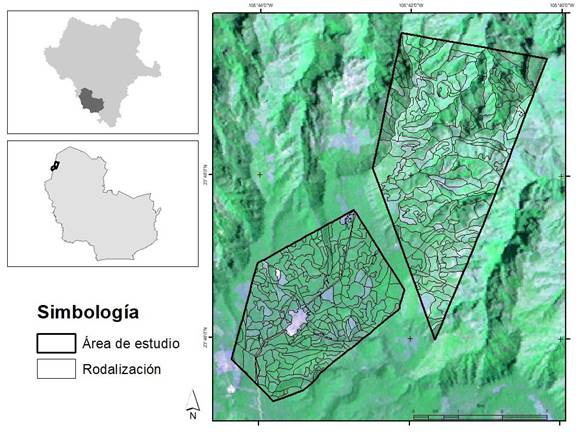
El área de estudio se localiza en la región suroeste del estado de Durango, México, concretamente, en los bosques del ejido Borbollones, Pueblo Nuevo (Figura 1), el cual se ubica en las coordenadas 23º 30’ y 24º 15’ LN, y 105º 15’ y 105º 45’ LO. El tipo de vegetación predominante corresponde a bosques mezclados con especies de los géneros Pinus y Quercus, principalmente. La altura sobre el nivel del mar varía de 1 400 a 3 000 m. El clima que prevalece es templado semifrío con un régimen de precipitación anual que fluctúa de 900 a 1 200 mm y una temperatura media anual que oscila de 8 °C en las partes más altas a 24 °C en las más bajas (García, 1981).
Datos de estudio
Los datos provienen de 441 parcelas temporales de muestreo de forma circular de 0.10 ha, obtenidos en el 2012 mediante un diseño de muestreo aleatorio estratificado con fines de manejo forestal maderable, cubriendo una superficie de 2 339.89 ha divididas en 263 unidades de manejo (rodales). Con la información de todas las especies registradas en cada parcela se estimaron las variables de rodal siguientes: número de árboles por hectárea (N; árboles·ha-1), área basal del rodal (G; m2·ha-1), diámetro medio cuadrático (dg; cm), altura dominante estimada como el promedio de los 100 árboles de mayor diámetro por hectárea (Hd; m) (Assmann, 1970) y volumen rollo total árbol (V; m3·ha-1). La composición de especies estimada fue 84 % para el género Pinus (P. ayacahuite Ehrenb., P. chihuahuana Schiede ex Schltdl. & Cham., P. cooperi Blanco, P. douglasiana Martínez, P. durangensis Martínez., P. engelmannii Carr., P. herrerae Martínez., P. leiophylla Schlecht. & Cham., P. lumholtzii B. L. Rob. & Fernald., P. michoacana Martínez., P. oocarpa Shiede. y P. teocote Schlecht. & Cham.); 8 % para el género Quercus (Q. candicans Neé, Q. crassifolia Ehrenb., Q. durifolia Seem., Q. eduardii Trel., Q. scytophylla Liebm., Q. obtusata Bonpl., Q. rugosa Neé, Q. sideroxila Humb. & Bonpl.); y 8 % para especies de los géneros Juniperus deppeana Steud., Cupressus lusitanica Mill. y Pseudotsuga menziesii (Mirb.) Franco. El Cuadro 1 muestra un resumen de los estadísticos principales de las variables involucradas en la construcción del DMD.
Cuadro 1 Resumen de la base de datos empleada en la construcción del diagrama de manejo de la densidad, para rodales mezclados del ejido Borbollones, Pueblo Nuevo, Durango, México.
| Variables de rodal | Mínimo | Máximo | Media ± DE |
|---|---|---|---|
| N (árboles·ha-1) | 173 | 1 180 | 503.73 ± 210.03 |
| dg (cm) | 15.40 | 46.20 | 26.83 ± 6.32 |
| Hd (m) | 11.20 | 20.70 | 15.70 ± 1.77 |
| V (m3·ha-1) | 40.60 | 343.10 | 142.65 ± 46.96 |
DE = desviación estándar de la media. N = número de árboles por hectárea; dg = diámetro cuadrático promedio; Hd = altura dominante; V = volumen.
Ecuaciones utilizadas
La estructura básica de un DMD está compuesta por dos ecuaciones alométricas ajustadas a partir de datos reales, y un índice de espesura del rodal que suele emplearse para caracterizar los tratamientos silvícolas a realizar. La primera de las ecuaciones relaciona el diámetro del árbol medio con la densidad del rodal y un indicador de su productividad. La segunda ecuación predice el volumen de productividad del rodal en función de las variables que definen el volumen del árbol medio y la densidad. A su vez, las variables de los ejes del DMD están condicionadas por el índice de caracterización de la espesura elegido, lo que obliga a que la densidad sea representada en términos del número de árboles por hectárea. En este trabajo se utilizó el índice de Hart-Becking “IHB” (Wilson, 1946), también conocido como índice de espaciamiento relativo, el cual se define como la razón (expresada en porcentaje) entre la distancia media de los árboles del rodal y la altura dominante. El IHB se emplea habitualmente para definir los límites superior e inferior de densidad, así como la necesidad, intensidad y frecuencia de los aclareos (Diéguez-Aranda et al., 2009); además, es independiente de la edad del rodal (Long, 1985) y puede ser adaptado para bosques regulares e irregulares (Gadow & Hui, 1999), representando, por tanto, una buena herramienta silvícola para el manejo de la densidad en rodales mezclados (Barrio-Anta & Álvarez-González, 2005).A partir de dos ejes de coordenadas que corresponden a la altura dominante (eje de las abscisas) y al número de árboles por hectárea (eje de las ordenadas) se representan las isolíneas de los valores del IHB y de las variables dependientes de las relaciones alométricas: una que relaciona el diámetro medio cuadrático con el número de árboles por hectárea y la altura dominante, y otra que relaciona el volumen del rodal con el número de árboles por hectárea, el diámetro medio cuadrático y la altura dominante como un indicador de la calidad de estación. Las expresiones de las ecuaciones empleadas en la construcción del DMD son las siguientes (despejando la densidad):
donde,
IHB |
índice de espacio de crecimiento relativo de Hart-Becking (%) |
d g |
diámetro medio cuadrático (cm) |
N |
densidad (árboles·ha-1) |
H d |
altura dominante (m) |
V |
volumen rollo total árbol (m3·ha-1) |
β i (i = 1 - 7) |
parámetros a estimar mediante mínimos cuadrados ordinarios no lineales |
Estas relaciones tienen consistencia silvícola y biológica; es decir, el valor del diámetro medio cuadrático va a estar condicionado por los tratamientos silvícolas (que determina los residuales del número de árboles por hectárea) y por la calidad de estación (caracterizada por la altura dominante). Por otro lado, el volumen del rodal está directamente relacionado con el área basal (cuyo valor depende del número de árboles por hectárea y del diámetro medio cuadrático) y con la altura dominante del rodal.
Para el cálculo del IHB se ha empleado la distancia media entre árboles correspondiente a un rodal con una distribución a tresbolillo, que se adecua más al estado actual de las masas estudiadas (Castaño-Santamaría, Barrio-Anta, & Álvarez-Álvarez, 2013). Teniendo en cuenta las ecuaciones anteriores, si se despeja N para cada una de ellas y se fijan valores distintos de IHB, dg y V, se pueden obtener las expresiones que permiten calcular las isolíneas o trayectorias que posteriormente se sobreponen en un diagrama cartesiano con Hd en el eje de las abscisas y N en el eje de las ordenadas, con lo cual queda el diagrama definido.
El sistema alométrico definido por las ecuaciones 2 y 3 tiene al dg como variable instrumental; es decir, el dg es la variable dependiente de la ecuación 2, mientras que en la ecuación 3 es una variable independiente. Por lo anterior, ambas ecuaciones se ajustaron de manera simultánea para evitar la correlación de errores. El ajuste de los parámetros se realizó mediante mínimos cuadrados ordinarios no lineales (ONLS) usando el procedimiento ‘nlsLM’ del paquete minpack.lm (Elzhov, Mullen, Spiess, & Bolker, 2013) en R (R Core Team, 2014).
El establecimiento de la línea del autoaclareo o límite superior del DMD se considera de importancia significativa, dada su utilidad en la simulación de la mortalidad natural o el autoaclareo y la prescripción de los aclareos; si esta línea no se considera, existe alta probabilidad de mortalidad por competencia. La regresión cuantílica ofrece la posibilidad de obtener la línea de densidad máxima y crear distintas líneas en cuantiles para rodales que superan los valores observados dentro del diagrama. La línea de densidad máxima se ajustó por regresión cuantílica no lineal (Koenker, & Bassett, 1978) con una ecuación potencial que relaciona el número de árboles por hectárea con la altura dominante:
El valor del cuantíl (τ) utilizado en el ajuste fue de 95 %; es decir, el límite superior de autoaclareo solo es superado por el 5 % de los rodales. Los parámetros a 1 y a 2 se estimaron mediante el uso de la función “nlrq” del módulo “quantreg” (Koenker, 2015) del programa R (R Core Team, 2014).
Evaluación de las relaciones alométricas
El análisis de la capacidad de ajuste de las relaciones alométricas se basó en las gráficas de los residuos y en los valores de los estadísticos coeficiente de determinación (R2) y raíz del error medio cuadrático (RMSE), cuyas expresiones matemáticas son las siguientes:
Resultados y discusión
Relaciones alométricas
Los estimadores de los parámetros β i de las ecuaciones 2 y 3 que definen el DMD (Cuadro 2) resultaron diferentes de cero con un nivel de significancia de 5 % (P < 0.05). El análisis de los residuales reveló que las ecuaciones de regresión no presentaron tendencias anómalas que hicieran suponer incumplimiento de las hipótesis de partida de normalidad, homogeneidad de varianza e independencia de los errores. Mediante el ajuste simultáneo de las ecuaciones 2 y 3, las variables independientes lograron explicar cerca de 87 % de la variabilidad observada de las variables dependientes, situación común para modelos estáticos de rodal (López-Sánchez & Rodríguez-Soalleiro, 2009), logrando minimizar el valor de la raíz del error medio cuadrático a 2.3. Estos resultados son consistentes con los rangos observados en la base de datos y muestran una estimación correcta del dg y V con la forma de las ecuaciones. La precisión en el ajuste de las ecuaciones 1 y 2 es aceptable al comparar los valores de R2 con trabajos desarrollados para rodales regulares de una o dos especies (Barrio Anta & Álvarez González, 2005; Castedo-Dorado et al., 2009; Tewari & Álvarez-González, 2014) y para rodales con mezcla de especies de los géneros Pinus, Quercus, Cupressus, Alnus y Juniperus (Corral-Rivas et al., 2015).
Cuadro 2 Parámetros estimados en el ajuste simultáneo de las ecuaciones* que definen el diagrama de manejo de la densidad.
| Parámetro | Estimador | EE | t | Pr > |t| |
|---|---|---|---|---|
|
|
1.735 | 0.4568 | 3.7996 | <0.0001 |
|
|
-0.188 | 0.0176 | -10.7020 | <0.0001 |
|
|
1.409 | 0.0641 | 21.9578 | <0.0001 |
|
|
1.155 | 1.1462 | 1.0076 | <0.0001 |
|
|
0.845 | 0.2244 | 3.7649 | <0.0001 |
|
|
0.305 | 0.0778 | 3.9176 | <0.0001 |
|
|
0.065 | 0.3808 | 0.1717 | <0.0001 |
EE = error estándar de los parámetros estimados; t = estadístico t de Student; Pr > |t| = probabilidad asociada al estimador del parámetro bajo una distribución de t de Student. *Ecuaciones:
Límite de densidad máxima
Los estimadores de los parámetros de la ecuación que determina la línea de autoaclareo (
Diagrama de manejo de la densidad
En la construcción del DMD, primeramente, se dibujó la línea de densidad máxima, utilizando la ecuación
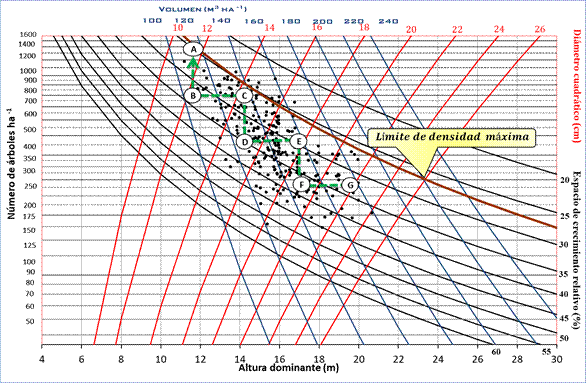
Figura 2 Ejemplo del uso del diagrama de manejo de la densidad desarrollado para rodales mezclados en un esquema de producción de madera para asierre al final del turno.
La Figura 2 ilustra un caso de estudio para el uso del DMD en un esquema de manejo, cuyo objetivo es la producción de madera para asierre al final del turno. En general, cualquier programa de manejo de la densidad en el diagrama se centra en maximizar la producción en volumen del rodal; por tanto, las opciones para el manejo de la densidad pueden ser representadas gráficamente a partir del eje de ordenadas (asumiendo que no existe mortalidad natural). La reducción de la densidad por los aclareos no causa efecto en la evolución de la altura dominante (eje de abscisas), por tanto, la velocidad con la que la masa se desplaza (edad de la altura dominante), a través del eje de abscisas, depende de la calidad de sitio o del crecimiento (Reineke, 1933). La producción total del rodal se puede obtener directamente de cualquier punto del diagrama a partir de las isolíneas que representan el volumen total. El volumen de la masa extraído, que deriva de las distintas intervenciones en forma de aclareos, se puede estimar como la diferencia entre los volúmenes antes y después de la intervención. La suma de estos volúmenes a lo largo del turno puede dar lugar a la estimación de la producción total bajo un régimen determinado de manejo silvícola.
En la Figura 2 se muestra un esquema de intervenciones silvícolas (recorridos entre los puntos A-B, C-D y E-F) en un rodal en particular que tendrá como objetivo la obtención de madera para asierre en la cosecha final (punto G del diagrama), el cual está definido por una altura dominante cercana a 20 m y un diámetro medio cuadrático de 20 cm, que dará un volumen promedio de 180 m3·ha-1. El esquema consiste en tres intervenciones (la primera corresponde a un aclareo comercial) dispuestas en el tiempo mediante el criterio biológico de crecimiento en altura dominante de más de cinco años (recorridos entre los puntos B-C, D-E, F-G), valor razonable para especies que crecen en buenas condiciones de sitio; para alcanzar el objetivo final (punto G), el esquema se presenta en una línea en forma de escalera (línea punteada). Los segmentos verticales representan las cortas de aclareo, mientras que los horizontales reflejan los intervalos entre los aclareos en un ciclo de corta de 10 años, asumiendo que después del aclareo no existirá mortalidad por competencia entre los individuos; sin embargo, se deberá tomar en cuenta que siempre existe la mortalidad por plagas, enfermedades o factores meteorológicos, lo cual no está considerado en el DMD. Dado que en el diagrama no figura la variable tiempo para definir el intervalo entre cortas, la altura dominante para el ciclo de corta se estimó utilizando la ecuación desarrollada por Corral-Rivas, Álvarez-González, Ruíz-González, y Gadow (2004); además, se consideró el número de tratamientos silvícolas aplicados a las masas regulares para un periodo de rotación de 60 años. De acuerdo con el diagrama, la primera intervención (punto B) se deberá realizar cuando el rodal alcance un diámetro medio cuadrático de 11 cm y 1 200 árboles·ha-1 con un IHB de 25 % que, en promedio, representa un volumen de 117 m3·ha-1. Los segmentos de las cortas intermedias fueron representados paralelos al eje de ordenadas bajo el supuesto de que los aclareos por lo bajo no afectan la altura dominante del rodal (López-Sánchez & Rodríguez-Soalleiro, 2009). En cuanto a la producción, esta puede ser obtenida en cualquier punto del diagrama utilizando las isolíneas de volumen del rodal. También es posible estimar el volumen de madera, según el destino industrial, a partir de las ecuaciones de volumen comercial ajustadas para las principales especies del área de estudio (Pérez-Cruzado, Merino, & Rodríguez-Soalleiro, 2011). La interpretación del programa de aclareos se puede apreciar con mayor detalle en el Cuadro 3.
Cuadro 3 Esquema de cortas a través del uso del diagrama de manejo de la densidad.
| Operación | Hd (m) | dg (cm) | IHB (%) | N (árboles·ha-1) | V (m3·ha-1) | EC (m) | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| ac | dc | ac | dc | ac | dc | ac | dc | |||
| Corta (A-B) | 11.8 | 11.7 | 12 | 26 | 34 | 1 100 | 750 | 115 | 105 | 3.06 |
| Corta (C-D) | 14.3 | 14.0 | 15 | 34 | 35 | 750 | 450 | 138 | 122 | 4.86 |
| Corta (E-F) | 16.7 | 16.5 | 18 | 29 | 38 | 450 | 260 | 150 | 140 | 4.84 |
| Corta final (G) | 19.5 | 21.8 | 33.5 | 260 | 170 | 6.53 | ||||
Hd = altura dominante; N = densidad; dg = diámetro medio cuadrático; V = volumen total del rodal; IHB = Índice de Hart-Becking; EC = espacio de crecimiento; ac = variable antes de la corta; y dc = variable después de la corta.
Conclusiones
Los resultados indican que la regresión cuantílica ofrece una alternativa para estimar de forma eficiente la línea de densidad máxima. El DMD desarrollado resulta útil para planificar y evaluar las cortas intermedias aplicadas a los bosques mezclados. El diagrama es una herramienta práctica para los manejadores forestales, ya que auxilia en la toma de decisiones en el manejo de la densidad del rodal para alcanzar diferentes objetivos, que en este caso fue la producción de madera. La altura dominante del rodal es la variable principal para considerar en la definición del periodo y frecuencia de los aclareos. Tal variable depende directamente de la calidad de sitio, composición de especies y edad, lo que permite maximizar el uso del sitio mediante un control adecuado de los niveles de densidad puntual y relativa.
Agradecimientos
Agradecemos a los ejidatarios del ejido Borbollones, Pueblo Nuevo, Durango, y al Dr. José Ascención Lujan Soto, Director Técnico de la UCODEFO “El Salto”, por permitirnos usar los datos de inventario del ejido y la información cartográfica. Nuestro agradecimiento también a los revisores anónimos y a los editores de la revista por sus valiosas sugerencias en este trabajo.
REFERENCIAS
Assmann, E. (1970). The principles of forest yield study: studies in the organic production, structure, increment and yield of forest stands. Oxford, UK: Pergamon Press. [ Links ]
Barrio-Anta, M., & Álvarez-González, J. G. (2005). Development of a stand density management diagram for even-aged pedunculated oak stands and its use in designing thinning schedules. Forestry, 78(3), 209-216. doi: 10.1093/forestry/ cpi033 [ Links ]
Barrio-Anta, M., Balboa-Murias, M. A., Castedo-Dorado, F., Dieguez-Aranda, U., & Álvarez-González, J. G. (2006). An ecoregional model for estimating volume, biomass and carbon pools in maritime pine stands in Galicia (northwestern Spain). Forest Ecology and Management, 223(1-3), 24-34. doi: 10.1016/j.foreco.2005.10.073 [ Links ]
Berger, A. L., & Puettmann, K. J. (2000). Overstory composition and stand structure influence herbaceous plant diversity in the mixed aspen forest of northern Minnesota. The American Midland Naturalist, 143(1), 111-125. Retrieved from https://blogs.cornell.edu/fieldbio2100/files/2016/10/Berger-Puetmann-2000-25ca3j7.pdf [ Links ]
Bi, H., Bruskin, S., & Smith, R. (2002). The zone of influence of paddock trees and the consequent loss in volume growth in young Eucalyptus dunnii plantations. Forest Ecology and Management, 165(1-3), 305-315. doi: 10.1016/S0378-1127(01)00632-6 [ Links ]
Bi, H., Wan, G., & Turvey, N. D. (2000). Estimating the self‐thinning boundary line as a density‐dependent stochastic biomass frontier. Ecology, 81(6), 1477-1483. doi: 10.1890/0012-9658(2000)081[1477:etstbl]2.0.co;2 [ Links ]
Castaño-Santamaría, J., Barrio-Anta, M., & Álvarez-Álvarez, P. (2013). Regional-scale stand density management diagrams for Pyrenean oak (Quercus pyrenaica Willd.) stands in north-west Spain. iForest, 6, 113-122. doi: 10.3832/ifor0880-006 [ Links ]
Castedo-Dorado, F., Crecente-Campo, F., Álvarez-Álvarez, P., & Barrio-Anta, M. (2009). Development of a stand density management diagram for radiata pine stands including assessment of stand stability. Forestry, 82(1), 1-16. doi: 10.1093/forestry/cpm032 [ Links ]
Comeau, P. G., White, M., Kerr, G., & Hale, S. E. (2010). Maximum density-size relationships for Sitka spruce and coastal Douglas-fir in Britain and Canada. Forestry, 83(5), 461-468. doi: 10.1093/forestry/cpq028 [ Links ]
Corral-Rivas, J. J., Álvarez-González, J. G., Ruíz-González, A. D., & Gadow, v. K. (2004). Compatible height and site index models for five pine species in El Salto, Durango (Mexico). Forest Ecology and Management, 201, 145-160. doi: 10.1016/j.foreco.2004.05.060 [ Links ]
Corral-Rivas, S., Álvarez-González, J. G., Corral-Rivas, J. J., Wehenkel, C., & López-Sánchez, C. A. (2015). Diagramas para el manejo de la densidad en bosques mixtos e irregulares de Durango, México. Bosque (Valdivia), 36(3), 409-421. doi: 10.4067/S0717-92002015000300008 [ Links ]
Daniel, T., Helms, J., & Baker, F. (1982). Principios de silvicultura (1.a ed.). México: McGraw-Hill. [ Links ]
del Rı́o, M., Montero, G., & Bravo, F. (2001). Analysis of diameter-density relationships and self-thinning in non-thinned even-aged Scots pine stands. Forest Ecology and Management, 142(1-3), 79-87. doi: 10.1016/S0378-1127(00)00341-8 [ Links ]
Diéguez-Aranda, U., Rojo-Alboreca, A., Castedo-Dorado, F., Álvarez González, J. G., Barrio-Anta, M., Crecente-Campo, F., …Sánchez-Rodríguez, F. (2009). Herramientas selvícolas para la gestión forestal sostenible en Galicia. España: Dirección Xeral de Montes, Consellería do Medio Rural, Xunta de Galicia. [ Links ]
Elzhov, T., Mullen, K., Spiess, A., & Bolker, B. (2013). Minpack.lm: R interface to the Levenberg-Marquardt nonlinear least-squares algorithm found in MINPACK, plus support for bounds. R package version 1.1-8. Retrieved from https://mran.microsoft.com/snapshot/2015-07-17/web/packages/minpack.lm/index.html [ Links ]
Gadow, K., & Hui, G. (1999). Modelling forest development. Forestry Sciences. The Netherlands: Kluwer Academic Publishers. doi: 10.1007/978-94-011-4816-0 [ Links ]
García, E. M. (1981). Modificaciones al sistema de clasificación climática de Köppen México: UNAM. [ Links ]
Koenker, R. (2015). quantreg: Quantile Regression. R package version 5.11. Retrieved from https://mran.microsoft.com/snapshot/2015-07-07/web/packages/quantreg/index.html [ Links ]
Koenker, R., & Bassett Jr, G. (1978). Regression quantiles. Econometrica, 46(1), 33-50. doi: 10.2307/1913643 [ Links ]
Long, J. N. (1985). A practical approach to density management. The Forestry Chronicle, 61(1), 23-27. Retrieved from http://pubs.cif-ifc.org/doi/pdf/10.5558/tfc61023-1 [ Links ]
López-Sánchez, C., & Rodríguez-Soalleiro, R. (2009). A density management diagram including stand stability and crown fire risk for Pseudotsuga menziesii (Mirb.) Franco in Spain. Mountain Research and Development, 29(2), 169-176. doi: 10.1659/mrd.1070 [ Links ]
Magaña, T. O. S., Torres, R. J. M., Rodríguez, F. C., Aguirre, D. H., & Fierros, G. A. M. (2008). Predicción de la producción y rendimiento de Pinus rudis Endl., en Aloapan, Oaxaca. Madera y Bosques, 14(1), 5-13. Retrieved from http://www.scielo.org.mx/pdf/mb/v14n1/v14n1a2.pdf [ Links ]
Márquez-Linares, M. A., & Álvarez-Zagoya, R. (1995). Construcción de una guía de densidad para Pinus cooperi var. ornelasi con base en la clase de copa en Durango, México. Madera y Bosques, 1(2), 23-36. Retrieved from http://www.redalyc.org/articulo.oa?id=61700204 [ Links ]
Minoche, D., Risio-Allione, L., Herrero, A. C., & Martínez-Zurimendi, P. (2017). Density management diagram for teak plantations in Tabasco, Mexico. iForest, 10(6), 909-915. doi: 10.3832/ifor2247-010 [ Links ]
Pérez-Cruzado, C., Merino, A., & Rodriguez-Soalleiro, R. (2011). A management tool for estimating bioenergy production and carbon sequestration in Eucalyptus globulus and Eucalyptus nitens grown as short rotation woody crops in northwest Spain. Biomass and Bioenergy, 35, 2839-2851. doi: 10.1016/j.biombioe.2011.03.020 [ Links ]
Quiñonez-Barraza, G., Tamarit-Urias, J. C., Martínez-Salvador, M., García-Cuevas, X., de los Santos-Posadas, H. M., & Santiago-García, W. (2018). Maximum density and density management diagram for mixed-species forests in Durango, Mexico. Revista Chapingo Serie Ciencias Forestales y del Ambiente, 24(1), 73-90. doi: 10.5154/r.rchscfa.2017.09.056 [ Links ]
R Core Team, R. C. (2014). R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing. [ Links ]
Reineke, L. H. (1933). Perfecting a stand-density index for even-aged forests. Journal of Agricultural Research, 46(7), 627-638. Retrieved from https://naldc.nal.usda.gov/ download/IND43968212/PDF [ Links ]
Santiago-García, W., de los Santos-Posadas, H. M., Ángeles- Pérez, G., Valdez-Lazalde, J. R., del Valle-Paniagua, D. H., & Corral-Rivas, J. J. (2013). Auto-aclareo y guías de densidad para Pinus patula mediante el enfoque de regresión de frontera estocástica. Agrociencia, 47, 75-89. Retrieved from http://www.scielo.org.mx/pdf/agro/v47n1/v47n1a7.pdf [ Links ]
Sturtevant, B. R., Bissonette, J. A., & Long, J. N. (1996). Temporal and spatial dynamics of boreal forest structure in western Newfoundland: Silvicultural implications for marten habitat management. Forest Ecology and Management, 87(1-3), 13-25. doi: 10.1016/S0378-1127(96)03837-6 [ Links ]
Tewari, V. P., & Álvarez-González, J. G. (2014). Development of a stand density management diagram for teak forests in southern India. Journal of Forest and Environmental Sciences, 30(3), 259-266. doi: 10.7747/JFS.2014.30.3.259 [ Links ]
Torres-Rojo, J. M., Velázquez-Martínez, A. (2000). Relative stand density index for mixed even-aged stands. Agrociencia, 34(4), 497-507. Retrieved from https://www.researchgate.net/publication/308142004_RELATIVE_STAND_DENSITY_INDEX_FOR_MIXED_EVEN-AGED_STANDS [ Links ]
Vacchiano, G., Motta, R., Long, J. N., & Shaw, J. D. (2008). A density management diagram for Scots pine (Pinus sylvestris L.): A tool for assessing the forest's protective effect. Forest Ecology and Management, 255(7), 2542-2554. doi: 10.1016/j.-foreco.2008.01.015 [ Links ]
Wilson, F. (1946). Numerical expression of stocking in terms of height. Journal of Forestry, 44(10), 758-761. doi: 10.1093/jof/44.10.758 [ Links ]
Yoda, K., Tatuo, K., Husato, O., & Kazuo, H. (1963). Self-thinning in overcrowded pure stands under cultivated and natural conditions. Journal of Biology Osaka City University, 14, 107-129. [ Links ]
Zhang, L., Bi, H., Gove, J. H., & Heath, L. S. (2005). A comparison of alternative methods for estimating the self-thinning boundary line. Canadian Journal of Forest Research, 35(6), 1507-1514. doi: 10.1139/x05-070 [ Links ]
Recibido: 26 de Marzo de 2018; Aprobado: 12 de Septiembre de 2018











 texto en
texto en