Introduction
A volume estimation system should be compatible; i.e., the stem volume obtained through the integration of a taper model should be equal to the volume predicted by the volume equation (Özçelik & Cao, 2017). Based on mass theory, an alternative for predicting sectional stem dry weight, at a given diameter at breast height (dbh) or total height, can be based on the integration of the taper equation and a function of wood density (Parresol & Thomas, 1989). Tree profile, volume and biomass are essential elements in forest management planning. Traditionally, these elements have been estimated separately, but the inclusion of wood density allows accurate simultaneous estimates (Parresol, 1999; Parresol & Thomas, 1989; Parresol & Thomas, 1996). Wood density can be modeled as a function of merchantable height or assumed to be constant, to determine the green weight or biomass of stems at any desired height (Brooks, Jiang, & Zhang, 2007; Jordan, Souter, Parresol, & Daniels, 2006; Valenzuela et al., 2018). The addition of wood density acquires relevance in the conversion of timber stocks to biomass and, particularly, for the estimation of carbon content (Ordóñez-Díaz et al., 2015).
Total biomass or by tree components (stem, bark, branches or foliage) can be estimated directly by equations with dbh and height data from forest inventories (Vargas-Larreta et al., 2017; Zhao, Kane, Markewitz, Teskey, & Clutter, 2015). On the other hand, when volume estimates are available, they can be converted to green weight or biomass through ratio equations (Zhao, Kane, Teskey, & Markewitz, 2016), or the corresponding taper and merchantable volume equations, to estimate variable biomass (Valenzuela et al., 2018). Indirect biomass estimates obtained from volume allow extensive transformation of volume data into biomass data (Ver Planck & MacFarlane, 2015). The demand for biomass equations has increased due to the need to improve estimation of forest carbon stocks and to quantify the distribution of wood biomass within trees (Ver Planck & MacFarlane, 2015). Quantification of the carbon concentration by components, and specifically in the branches, has taken on importance for bioenergy or CO2 quantification (Corral-Rivas et al., 2017).
Trees, without considering the roots, are commonly separated into four components: stump, main stem, stem bark and live crown, which are used to refer to volume, green weight, biomass (Parresol, 2001) and, frequently, carbon. According to Ver Planck and MacFarlane (2015), there are three main procedures for estimating biomass: prediction through predictor variables, (2) prediction from volume, or (3) simultaneous estimation of both biomass and volume components.
Carbon is an important element in the forest wood value chain and represents an essential product on the global market (Zakrzewski & Duchesne, 2012). Quantifying carbon sources and sinks and their spatial distribution and dynamics over time is a global research focus (Zakrzewski & Duchesne, 2012). If taper, green weight and carbon concentration are integrated into the simultaneous volume and biomass estimates, a compatible system for the simultaneous estimation of the five variables can be considered. Therefore, the objective of this study was to develop a compatible taper, volume, green weight, biomass and carbon concentration system for Quercus sideroxyla Bonpl. in Durango, Mexico.
Materials and methods
Study area and experimental data
The study area was the ejido San Diego de Tezains, located in Forest Management Unit 1005, Santiago Papasquiaro y Anexos, in the state of Durango, between the geographic coordinates 24° 48’ 16.98” - 25° 13’ 47.25” N and 105° 53’ 09.81” - 106° 12’ 52.58” W. The total area is 60 801.92 ha, with the forest covering 26 039.02 ha (Quiñonez-Barraza, De los Santos-Posadas, Álvarez-González, & Velázquez-Martínez, 2014). The predominant climate is temperate semi-cold humid -C(E)(w2)(x’) - with a mean annual temperature of 5 to 12 °C and average annual rainfall of 840 mm (García, 2004).
Quercus sideroxyla is a commercial timber species distributed in mixed-species stands in which the genus Pinus is dominant. The database was integrated with 37 trees (522 merchantable diameter-height measurements) distributed in stands with forest management and collected in 2006 to generate the local biometric system. Tree selection considered stem straightness, a regular live crown, dominance and distribution of diameters and heights. The trees were felled and the diameters and heights on the stem were measured. Measurements on the stem were recorded considering the taper at the height of the dbh (four measurements) and then sections of 2 m to tree top. Merchantable branches (basal diameter ≥ 2 cm) were measured at variable lengths. The volume of the bolts and stem was estimated using the overlapping bolts method proposed by Bailey (1995), while branch volume was estimated using the Smalian and cone formulas (Quiñonez-Barraza et al., 2014). Figure 1 shows the dispersion of relative outside-bark and inside-bark volume with respect to relative height, and Table 1 presents the variables used.
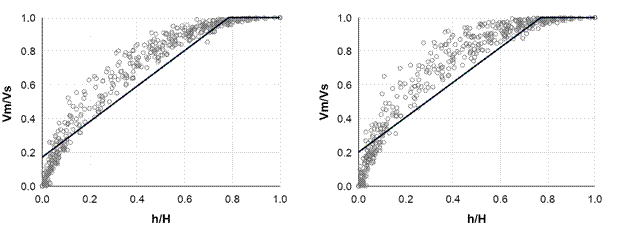
Figure 1 Relative volume (Vm/Vs) by relative height (h/H) data, outside-bark (left) and inside-bark (right). Vm: merchantable volume, Vs: stem volume, h: upper-height, H: total height.
Table 1 Database used in fitting of the compatible taper, volume, green weight, biomass and carbon concentration system for Quercus sideroxyla.
| Variable | outside-bark | inside-bark | ||||||
|---|---|---|---|---|---|---|---|---|
| Minimum | Maximum | Mean | SD | Minimum | Maximum | Mean | SD | |
| d (cm) | 0.000 | 67.000 | 20.314 | 13.435 | 0.000 | 60.000 | 16.513 | 11.951 |
| D (cm) | 11.000 | 48.000 | 27.090 | 10.170 | 9.000 | 42.000 | 23.008 | 8.806 |
| H (m) | 6.600 | 21.000 | 12.867 | 4.092 | - | - | - | - |
| h (m) | 0.000 | 21.000 | 5.447 | 4.947 | - | - | - | - |
| hs (m) | 0.070 | 0.340 | 0.181 | 0.064 | - | - | - | - |
| Vs (m3) | 0.041 | 2.054 | 0.501 | 0.494 | 0.025 | 1.579 | 0.330 | 0.345 |
| Vm (m3) | 0.000 | 2.054 | 0.310 | 0.410 | 0.000 | 1.579 | 0.210 | 0.285 |
| Vb (m3) | 0.047 | 2.440 | 0.586 | 0.584 | 0.032 | 1.783 | 0.388 | 0.395 |
| Vt (m3) | 0.003 | 0.387 | 0.085 | 0.098 | 0.002 | 0.245 | 0.058 | 0.065 |
| Wsg (kg) | 57.839 | 2 895.483 | 706.936 | 696.835 | 35.622 | 2226.204 | 465.297 | 486.070 |
| Wmg (kg) | 0.000 | 2 895.483 | 437.177 | 578.471 | 0.000 | 2226.204 | 296.073 | 402.258 |
| Wtg (kg) | 66.286 | 3 440.598 | 826.095 | 823.941 | 44.592 | 2513.792 | 547.436 | 557.510 |
| Wbg (kg) | 3.983 | 545.115 | 119.158 | 138.565 | 3.278 | 344.913 | 82.139 | 91.527 |
| Wsd (kg) | 25.474 | 1 275.244 | 311.353 | 306.904 | 15.689 | 980.477 | 204.929 | 214.078 |
| Wmd (kg) | 0.000 | 1 275.244 | 192.544 | 254.773 | 0.000 | 980.477 | 130.398 | 177.165 |
| Wtd (kg) | 29.194 | 1 515.327 | 363.833 | 362.885 | 19.639 | 1 107.138 | 241.105 | 245.542 |
| Wbd (kg) | 1.754 | 240.083 | 52.480 | 61.027 | 1.444 | 151.908 | 36.176 | 40.311 |
| Cs (kg) | 12.737 | 637.622 | 155.676 | 153.452 | 7.844 | 490.239 | 102.464 | 107.039 |
| Cm (kg) | 0.000 | 637.622 | 96.272 | 127.387 | 0.000 | 490.239 | 65.199 | 88.582 |
| Ct (kg) | 14.597 | 757.664 | 181.917 | 181.442 | 9.820 | 553.569 | 120.552 | 122.771 |
| Cb (kg) | 0.877 | 120.041 | 26.240 | 30.514 | 0.722 | 75.954 | 18.088 | 20.155 |
SD = standard deviation of the mean, d = taper, D = diameter at breast height (dbh), H = total height, h = upper-height, hs = stump height, Vs = stem volume, Vm = merchantable volume, Vb = branch volume, Vt = total tree volume, Wsg = stem green weight, Wmg = merchantable green weight, Wtg = total tree green weight, Wbg = branch green weight, Wsd = stem biomass, Wmd = merchantable biomass, Wtd = total tree biomass, Wbd = branch biomass, Cs = stem carbon concentration, Cm = merchantable carbon concentration, Ct = total tree carbon concentration, Cb = branch carbon concentration.
Description of the Quercus sideroxyla compatible system
Some of the volume and biomass equations, based on wood density, are founded on the approach proposed by Parresol and Thomas (1989), which consists of determining dry weight or dry biomass as a function that multiplies volume by wood density and can be obtained as:
where,
w |
weight of stem section between lower (hl) and upper (hu) height for total height (H) |
f(h) |
taper equation in the cross-sectional area of the stem |
ρ(h, Y) |
function of density in the cross-sectional area (Y) as a dimension of tree height |
In practice, the double-integral model is simplified to one integral because the relative density is usually constant in the Y dimension. Therefore, the weight of bolts or stems can be obtained according to what is expressed by Parresol and Thomas (1996):
Based on the procedure described by Zhang,
Borders, and Bailey (2002), the merchantable volume equation is
integrated with the density function (
If a taper function is used that considers a compatible merchantable volume, the merchantable weight (W m , kg) would be given by multiplying the basic density of the wood (ρ 0 , kg·m-3) and the corresponding merchantable volume equation (V m , m3) (Brooks, Jiang, & Clark III, 2007). This can be expressed as:
Green density (ρ 0g ) and basic density (ρ 0d ) were used to model green weight (W g ) and dry biomass (W d ), respectively. These density concepts have been used in biomass studies for forest species in Mexico and North America (Miles & Smith, 2009; Nájera et al., 2007; Návar, 2009; Ordóñez-Díaz et al., 2015; Pérez, Dávalos-Sotelo, Limón, & Quintanar, 2015; Pérez-Olvera & Dávalos-Sotelo, 2008). According to the average values reported in these studies and considering the proximity to the study area, the value used for ρ 0g was 1 410 kg·m-3, and for ρ 0d , 621 kg·m-3, and 49 % of the ρ 0d was used for carbon concentration (ρ 0c ) of 304.29 kg·m-3 as a reasonable amount for the species Q. sideroxyla (Aquino-Ramírez, Velázquez-Martínez, Echevers-Barra, & Castellanos-Bolaños, 2018; Návar, 2009; Silva-Arredondo & Návar-Cháidez, 2009; Vargas-Larreta et al., 2017).
In this study, the compatible taper and merchantable volume system reported by Fang, Borders, and Bailey (2000) was used, and green weight, biomass, and carbon concentration were included. The system is integrated by the taper and merchantable volume equations (Equations 1 and 2, respectively):
with the following expressions,
where,
h ij |
upper-height j of tree i (m) |
d ij(ob) |
diameter j of tree i at height h ij (cm) |
|
merchantable outside-bark volume (m3) j, outside-bark green weight (kg) j, outside-bark biomass (kg) and outside-bark carbon concentration (kg) j, respectively, of tree i at height h ij |
H i |
total height of tree i (m) |
D i(ob) |
outside-bark dbh of tree i (cm) |
h s |
stump height of tree i (m) |
α i |
total volume parameters (i = 0, 1, 2) |
β i |
taper and merchantable volume parameters (i = 1, 2, 3) |
|
inflection point parameters |
ε ij |
error j in tree i |
ρ 0i |
density value for W sg(ob) , W sd(ob) and C s(ob) , which were assumed constants, which did not apply for V s(ob) in the stem volume equation |
The CS included taper (d), stem volume (V s ), merchantable volume (V m ), total tree volume (V t ) and branch volume (V b ) equations. These components were the basis of the CS and defined the set of equations for W g , W d and C.
The stem volume equation was the one reported by Schumacher (1933) and is given in Equation 3, the total tree volume equation (V s + V b ) is given in Equation 4 and that of branch volume in Equation 5, for all variables:
where,
V s(ob , V t(ob) and V b(ob) |
stem outside-bark volume, total tree outside-bark volume and branches outside-bark volume (m3), respectively |
W sg(ob), W tg(ob) and W bg(ob) |
green stem outside-bark weight, green total tree outside-bark weight and green branches outside-bark weight (kg), respectively. |
W sd(ob) , W td(ob) and W bd(ob) |
stem outside-bark biomass, total tree outside-bark biomass and branches outside-bark biomass (kg), respectively |
C s(ob) , C t(ob) and C b(ob) |
stem outside-bark carbon concentration, total tree outside-bark carbon concentration and branches outside-bark carbon concentration (kg), respectively. |
(ob) |
outside-bark components |
ρ 0i |
density corresponding to W sg(ob) , W sd(ob) and C s(ob) , which does not apply for V s(ob) in the stem volume equation |
α i (i = 1, 2) |
common parameters for V s(ob) , W sg(ob) , W sd(ob) and C s(ob) |
α 0i (i = 1, 2, 3, 4) |
specific parameters for each equation (i = 1 for V s(ob) , i = 2 for W sg(ob) , i = 3 for W sd(ob) and i = 4 for C s(ob) ), which were scaled with the known density parameters (ρ 0i ). The same procedure in δ i and δ 0i for total tree |
The outside-bark equations were modeled inside-bark with the addition of a proportion parameter, as follows:
where,
(ib) |
inside-bark component |
θ 0 |
parameter representing the taper equation |
f(d ij(ob) ) |
taper function |
θ 1i |
parameters representing merchantable volume, green weight, dry biomass and carbon concentration |
|
merchantable volume function |
θ 2i , θ 3i y θ 4i |
parameters representing the stem inside-bark volume, total tree inside-bark volume and branch inside-bark volume equations (i = 1, 2, 3, 4) |
Fitting of the compatible system
The CS was simultaneously fitted by generalized nonlinear least squares (GNLS) of
the SAS® MODEL procedure (SAS
Institute Inc., 2015). In addition, a continuous autoregressive error
structure (CAR2) was included to correct the autocorrelation in
the taper, as well as a power function [
Fitting statistics
Goodness-of-fit of the CS was evaluated with global statistics such as root mean square error (RMSE), adjusted coefficient of determination (R2), mean Bias and Akaike information criterion (AIC). The standard error of estimate (SEE), R2 and bias were used per relative height classes for the taper and merchantable equations.
Results and discussion
The 34 CS equations were simultaneously fitted and the 36 parameters were different from zero at a significance level of 1 % (p < 0.01). The fitting guaranteed the compatibility of the equations, and the parameter errors were simultaneously minimized (Brooks, Jiang, & Clark III, 2007; Jiang & Brooks, 2008). The base parameters of the taper equation and the merchantable stem and total tree volumes defined the global and specific parameters for the rest of the variables, both outside-and inside-bark components (Table 2). The use of green density, basic density and percentage of biomass for carbon concentration allowed modeling the five variables in the stem, total tree and branch components. This procedure was similar to that proposed by Parresol and Thomas (1989), but assuming constant density along the tree stem. Brooks, Jiang, and Zhang (2007), and Ver Planck and MacFarlane (2015) found similar results in predicting biomass with a merchantable volume function.
Table 2 Estimate parameters of compatible system equations for taper, volume, green weight, biomass and carbon concentration of Quercus sideroxyla.
| Parameter | Estimate | SE | t | p | Parameter | Estimate | SE | t | p |
|---|---|---|---|---|---|---|---|---|---|
|
|
0.00003 | 7.1×10−6 | 39.81 | <0.0001 |
|
0.00963 | 0.00024 | 39.82 | <0.0001 |
|
|
2.17879 | 0.00959 | 227.18 | <0.0001 |
|
0.82130 | 0.00672 | 122.22 | <0.0001 |
|
|
0.85272 | 0.00902 | 94.50 | <0.0001 |
|
0.70054 | 0.00801 | 87.45 | <0.0001 |
|
|
0.00001 | 3.6×10−6 | 18.20 | <0.0001 |
|
0.72230 | 0.00685 | 105.47 | <0.0001 |
|
|
0.00002 | 1.4×10−5 | 12.50 | <0.0001 |
|
0.68538 | 0.00652 | 105.13 | <0.0001 |
|
|
0.00003 | 4.7×10−6 | 66.37 | <0.0001 |
|
0.52499 | 0.01700 | 30.90 | <0.0001 |
|
|
0.04643 | 0.00382 | 12.14 | <0.0001 |
|
0.65491 | 0.00746 | 87.84 | <0.0001 |
|
|
0.18090 | 0.01890 | 9.55 | <0.0001 |
|
0.66609 | 0.00611 | 108.93 | <0.0001 |
|
|
0.68358 | 0.05860 | 11.67 | <0.0001 |
|
0.66270 | 0.00620 | 106.96 | <0.0001 |
|
|
0.20490 | 0.03360 | 6.10 | <0.0001 |
|
0.64401 | 0.02130 | 30.29 | <0.0001 |
|
|
0.00004 | 0.00001 | 37.48 | <0.0001 |
|
0.65491 | 0.00746 | 87.84 | <0.0001 |
|
|
2.20564 | 0.01020 | 216.06 | <0.0001 |
|
0.66609 | 0.00611 | 108.94 | <0.0001 |
|
|
0.80209 | 0.00924 | 86.84 | <0.0001 |
|
0.66270 | 0.00620 | 106.96 | <0.0001 |
|
|
0.05334 | 0.00142 | 37.53 | <0.0001 |
|
0.64401 | 0.02130 | 30.29 | <0.0001 |
|
|
0.02349 | 0.00063 | 37.53 | <0.0001 |
|
0.65226 | 0.00739 | 88.23 | <0.0001 |
|
|
0.01178 | 0.00031 | 37.51 | <0.0001 |
|
0.66221 | 0.00605 | 109.39 | <0.0001 |
|
|
0.04346 | 0.00109 | 39.89 | <0.0001 |
|
0.66052 | 0.00616 | 107.17 | <0.0001 |
|
|
0.01914 | 0.00048 | 39.89 | <0.0001 |
|
0.65157 | 0.02160 | 30.20 | <0.0001 |
SE = standard error; t = Student's t-distribution value; p = value of the probability associated with the t value. d = taper, Vs = stem volume, Vm = merchantable volume, Vt = total tree volume, Vb = branch volume, Wsg = stem green weight, Wmg = merchantable green weight, Wtg = total tree green weight, Wbg = branch green weight, Wsd = stem biomass, Wmd = merchantable biomass, Wtd = total tree biomass, Wbd = branch biomass, Cs = stem carbon concentration, Cm = merchantable carbon concentration, Ct = total tree carbon concentration, Cb = branch carbon concentration, ob = outside-bark, ib = inside-bark.
The lowest inflection point occurs at 4.64 % of total height, while the highest inflection point occurs at 18.09 % (Table 2). The normalized form factors of the three segments were 0.086, 0.229 and 0.407 (Fang et al., 2000), suggesting a strong taper below 20 % relative height, while the stem has a better form after that height; this behavior is common in this species. Vargas-Larreta et al. (2017) fitted a regional model for the species, in which they suggest form factors similar to those found.
The fitting statistics showed the accuracy of the CS equations, which are presented in Table 3. The lowest R2 values were found for the branch component: 0.742 outside-bark and 0.668 for inside-bark components; however, these statistics are considered efficient, if compared with the low values reported by Simental-Cano et al. (2017) for different species, among them Q. sideroxyla (R2 = 0.48). The improved fitting is due to the fact that the merchantable branch volume considered all the merchantable branches for each tree and not only the branches with a basal diameter greater than 5 cm, as considered by Vargas-Larreta et al. (2017) in developing a forest biometric system for some forests in Mexico. In addition, volume, green weight, biomass and carbon concentration estimation can be made at desired upper-heights and diameters, which involves an important gain compared to models based on allometric relationships and expansion factors such as those of Návar (2009), and Silva-Arredondo and Návar-Cháidez (2009). In the other CS equations, the lowest R2 values were 0.959 and 0.923 for outside-bark and inside-bark diameters, respectively. Because the outside- and inside-bark components for green weight, biomass and carbon concentration equations were scaled from the merchantable volume of the stem, total tree and branches, the R2 values were the same for the sets of equations, but those of RMSE, AIC and Bias were different.
Table 3 Fitting statistics of the compatible system equation components of taper, volume, green weight, biomass and carbon concentration of Quercus sideroxyla.
| Variable | Outside-bark | Inside-bark | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| np | RMSE | R2 | AIC | Bias | np | RMSE | R2 | AIC | Bias | |
| d (cm) | 10 | 2.708 | 0.959 | 1052 | 0.167 | 11 | 3.320 | 0.923 | 1266 | 0.099 |
| Vm (m3) | 8 | 0.065 | 0.975 | -2835 | 0.032 | 9 | 0.072 | 0.936 | -2733 | 0.013 |
| Vs (m3) | 3 | 0.023 | 0.965 | -3955 | 0.003 | 4 | 0.022 | 0.931 | -3992 | 0.000 |
| Vt (m3) | 3 | 0.026 | 0.967 | -3821 | 0.002 | 4 | 0.026 | 0.926 | -3810 | 0.001 |
| Vb (m3) | 6 | 0.014 | 0.742 | -4458 | -0.001 | 7 | 0.012 | 0.668 | -4599 | 0.000 |
| Wmg (kg) | 8 | 75.316 | 0.983 | 4524 | 12.683 | 9 | 101.587 | 0.936 | 4837 | 18.067 |
| Wsg (kg) | 3 | 25.976 | 0.977 | 3405 | 1.076 | 4 | 30.620 | 0.931 | 3578 | 0.503 |
| Wtg (kg) | 3 | 34.938 | 0.970 | 3715 | 0.967 | 4 | 36.448 | 0.926 | 3760 | 0.983 |
| Wbg (kg) | 6 | 17.288 | 0.742 | 2983 | -0.109 | 7 | 17.042 | 0.668 | 2969 | 0.475 |
| Wmd (kg) | 8 | 33.171 | 0.983 | 3668 | 5.586 | 9 | 44.741 | 0.936 | 3981 | 7.957 |
| Wsd (kg) | 3 | 11.440 | 0.977 | 2549 | 0.474 | 4 | 13.486 | 0.931 | 2722 | 0.221 |
| Wtd (kg) | 3 | 15.387 | 0.970 | 2859 | 0.426 | 4 | 16.053 | 0.926 | 2904 | 0.433 |
| Wbd (kg) | 6 | 7.614 | 0.742 | 2127 | -0.048 | 7 | 7.506 | 0.668 | 2113 | 0.209 |
| Cm (kg) | 8 | 16.655 | 0.983 | 2948 | 2.245 | 9 | 22.343 | 0.937 | 3256 | 3.869 |
| Cs (kg) | 3 | 5.728 | 0.977 | 1827 | 0.182 | 4 | 6.743 | 0.931 | 1998 | 0.111 |
| Ct (kg) | 3 | 7.696 | 0.970 | 2136 | 0.176 | 4 | 8.026 | 0.926 | 2180 | 0.216 |
| Cb (kg) | 6 | 3.809 | 0.742 | 1404 | -0.005 | 7 | 3.752 | 0.668 | 1390 | 0.104 |
np = number of parameters in the equation, RMSE = root mean square error, R2 = adjusted coefficient of determination, AIC = Akaike information criterion, d = taper, Vm = merchantable volume, Vs = stem volume, Vt = total tree volume, Vb = branch volume, Wmg = merchantable green weight, Wsg = stem green weight, Wtg = total tree green weight, Wbg = branch green weight, Wmd = merchantable biomass, Wsd = stem biomass, Wtd = total tree biomass, Wbd = branch biomass, Cm = merchantable carbon concentration, Cs = stem carbon concentration, Ct = total tree carbon concentration, Cb = branch carbon concentration.
The variation in
The fitting statistics by relative height classes are shown in Table 4. The 10 % class considered merchantable measurements from the base and around the dbh. The lowest efficiency was found in the extreme classes, i.e., at stump height and in the 90 % class. The latter is associated with the number of observations (16) and CS restrictions on top diameter.
Table 4 Fitting statistics for the relative height classes of the compatible system equation components of taper, volume, green weight, biomass and carbon concentration of Quercus sideroxyla.
| h/H (%) | n | outside-bark | inside-bark | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| d (cm) | Vm (m3) | Wmg (kg) | Wmd (kg) | Cm (kg) | d (cm) | Vm (m3) | Wmg (kg) | Wmd (kg) | Cm (kg) | ||
| SEE | |||||||||||
| 10 | 178 | 3.632 | 0.028 | 38.412 | 16.919 | 8.449 | 4.106 | 0.024 | 34.167 | 15.076 | 7.519 |
| 20 | 26 | 2.897 | 0.022 | 47.410 | 20.817 | 10.854 | 3.511 | 0.038 | 54.310 | 23.889 | 11.966 |
| 30 | 29 | 2.365 | 0.029 | 65.414 | 28.714 | 15.024 | 3.116 | 0.043 | 60.347 | 26.612 | 13.284 |
| 40 | 36 | 2.096 | 0.059 | 68.870 | 30.295 | 15.434 | 3.667 | 0.080 | 109.573 | 48.459 | 24.091 |
| 50 | 50 | 2.101 | 0.055 | 64.113 | 28.222 | 14.236 | 2.800 | 0.068 | 94.284 | 41.591 | 20.750 |
| 60 | 49 | 1.899 | 0.071 | 77.653 | 34.198 | 17.147 | 2.434 | 0.078 | 106.835 | 47.251 | 23.489 |
| 70 | 57 | 2.044 | 0.081 | 83.061 | 36.597 | 18.230 | 2.829 | 0.098 | 137.765 | 60.692 | 30.335 |
| 80 | 43 | 1.602 | 0.100 | 102.587 | 45.197 | 22.538 | 2.347 | 0.116 | 162.924 | 71.748 | 35.881 |
| 90 | 16 | 2.151 | 0.163 | 172.223 | 75.886 | 37.769 | 2.685 | 0.161 | 220.525 | 97.663 | 48.459 |
| 100 | 38 | 0.528 | 0.088 | 109.245 | 48.095 | 24.207 | 0.683 | 0.073 | 116.337 | 43.450 | 21.788 |
| R2 | |||||||||||
| 10 | 178 | 0.903 | 0.788 | 0.803 | 0.803 | 0.804 | 0.843 | 0.729 | 0.734 | 0.733 | 0.735 |
| 20 | 26 | 0.911 | 0.985 | 0.967 | 0.967 | 0.964 | 0.822 | 0.915 | 0.914 | 0.914 | 0.914 |
| 30 | 29 | 0.937 | 0.990 | 0.973 | 0.974 | 0.971 | 0.845 | 0.955 | 0.956 | 0.956 | 0.956 |
| 40 | 36 | 0.949 | 0.980 | 0.986 | 0.986 | 0.986 | 0.805 | 0.934 | 0.937 | 0.936 | 0.937 |
| 50 | 50 | 0.900 | 0.971 | 0.980 | 0.980 | 0.980 | 0.742 | 0.913 | 0.915 | 0.914 | 0.915 |
| 60 | 49 | 0.916 | 0.972 | 0.983 | 0.983 | 0.983 | 0.771 | 0.935 | 0.938 | 0.938 | 0.939 |
| 70 | 57 | 0.875 | 0.967 | 0.983 | 0.983 | 0.983 | 0.650 | 0.900 | 0.900 | 0.900 | 0.900 |
| 80 | 43 | 0.841 | 0.961 | 0.979 | 0.979 | 0.979 | 0.555 | 0.893 | 0.894 | 0.894 | 0.894 |
| 90 | 16 | 0.484 | 0.938 | 0.965 | 0.965 | 0.965 | 0.140 | 0.895 | 0.901 | 0.900 | 0.902 |
| 100 | 38 | 0.784 | 0.963 | 0.971 | 0.971 | 0.970 | 0.508 | 0.946 | 0.930 | 0.950 | 0.949 |
| Bias | |||||||||||
| 10 | 178 | -0.227 | 0.020 | 24.563 | 10.827 | 5.353 | 1.012 | 0.017 | 24.055 | 10.628 | 5.291 |
| 20 | 26 | 0.654 | 0.011 | -11.227 | -4.881 | -2.880 | -0.102 | 0.008 | 8.678 | 4.065 | 1.864 |
| 30 | 29 | -0.082 | 0.012 | -19.217 | -8.377 | -4.784 | -0.403 | 0.017 | 19.763 | 9.034 | 4.288 |
| 40 | 36 | 0.864 | 0.030 | -3.137 | -1.273 | -1.388 | -0.007 | 0.020 | 23.860 | 10.925 | 5.173 |
| 50 | 50 | 0.394 | 0.030 | 6.312 | 2.867 | 0.834 | -0.821 | 0.015 | 17.665 | 8.112 | 3.825 |
| 60 | 49 | 0.513 | 0.037 | 7.235 | 3.294 | 0.906 | -0.454 | 0.023 | 27.036 | 12.318 | 5.874 |
| 70 | 57 | 0.192 | 0.047 | 15.051 | 6.751 | 2.531 | -0.788 | 0.007 | 3.904 | 2.187 | 0.769 |
| 80 | 43 | 0.191 | 0.065 | 21.589 | 9.675 | 3.689 | -0.583 | 0.002 | -5.073 | -1.598 | -1.241 |
| 90 | 16 | 0.557 | 0.089 | 9.189 | 4.327 | 0.234 | 0.421 | 0.049 | 55.966 | 25.717 | 12.117 |
| 100 | 38 | 0.086 | 0.039 | 4.847 | 2.253 | 0.308 | 0.111 | -0.019 | 9.452 | 0.689 | 0.538 |
h/H = relative height; n = number of observations per relative height classes; SEE = standard error of estimate, R2 = adjusted coefficient of determination, d = taper, Vm = merchantable volume, Wmg = merchantable green weight, Wmd = merchantable biomass, Cm = merchantable carbon concentration.
The residuals per relative height classes (h/H) and total height (H), for taper and volume, are presented in box and whisker plots in Figure 2, for green weight in Figure 3, for biomass in Figure 4 and for carbon concentration in Figure 5. The CS modeled biomass and carbon concentration with high statistical precision, which will allow quantification of these variables for complete trees, as well as merchantable heights and inclusion in forest inventories. Similar patterns have been reported by Fang et al. (2000) for volume and taper and by Kozak and Smith (1993) for taper in standard error of estimate and average Bias.
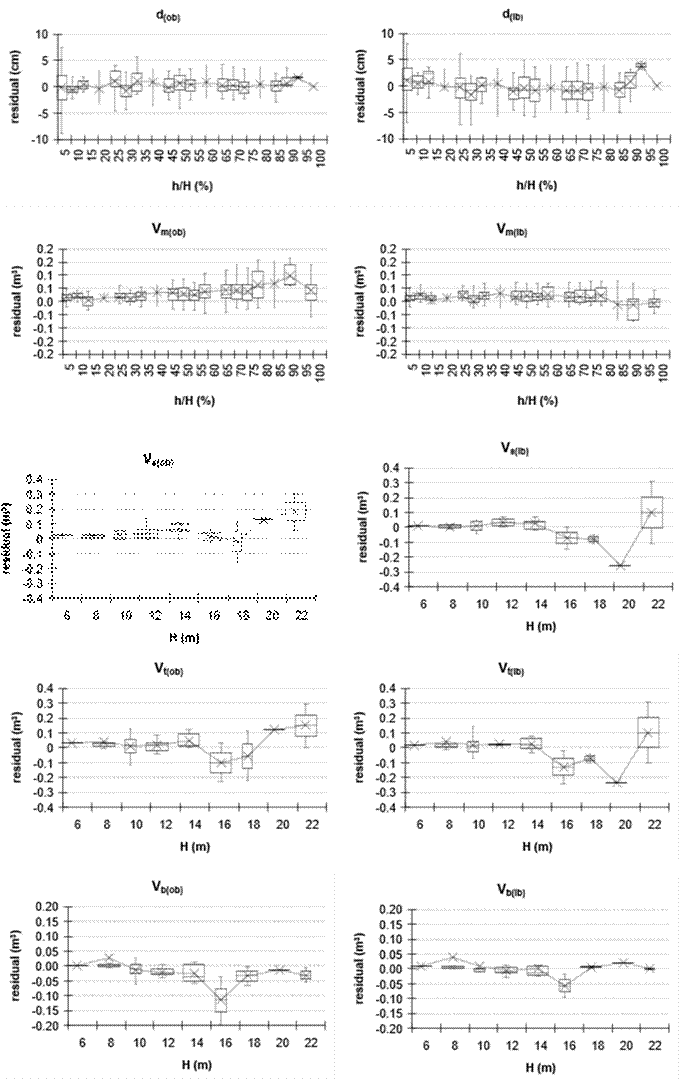
Figure 2 Dispersion of the residuals of taper (d) and merchantable volume (Vm) with respect to relative height (h/H), and of stem (Vs), total tree (Vt) and branch (Vb) volumes with respect to total height (H), outside-bark (ob) and inside-bark (ib).
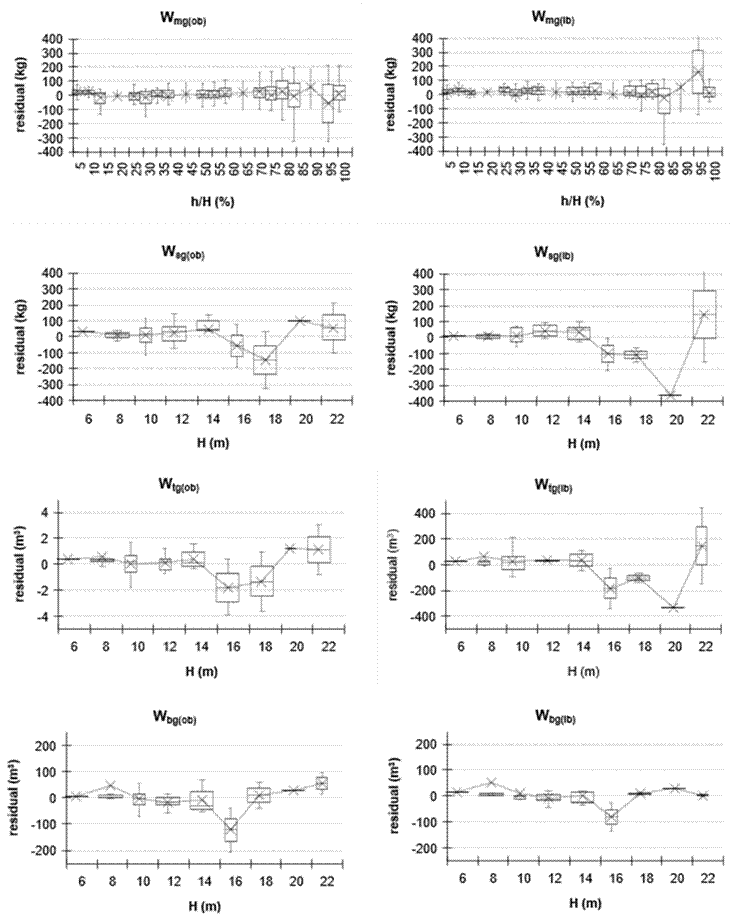
Figure 3 Dispersion of the residuals of merchantable green weight (Wmg) with respect to relative height (h/H), and of stem (Wsg), total tree (Wtg) and branch (Wbg) green weight with respect to total height (H), outside-bark (ob) and inside-bark (ib).
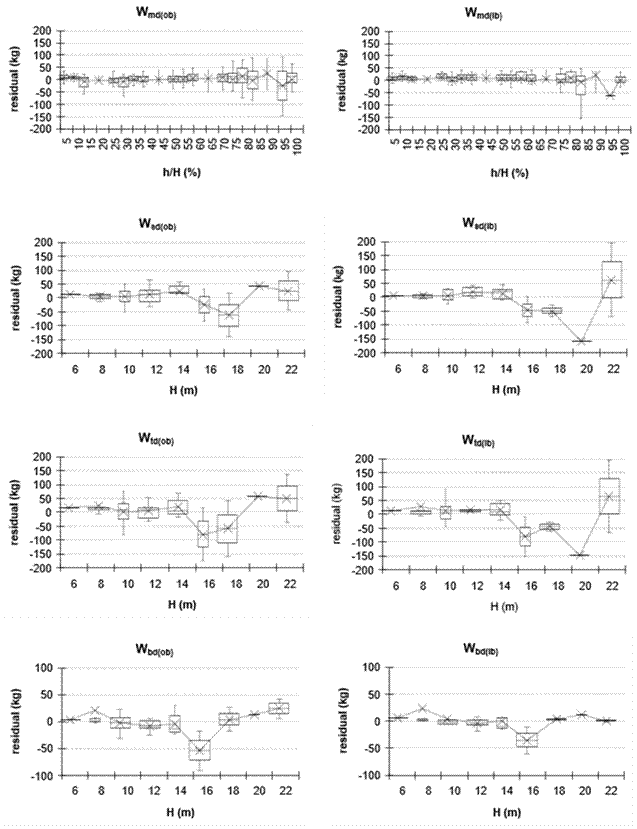
Figure 4 Dispersion of the residuals of merchantable biomass (Wmd) with respect to relative height (h/H), and of stem (Wsd), total tree (Wtd) and branch (Wbd) biomass with respect to total height (H), outside-bark (ob) and inside-bark (ib).
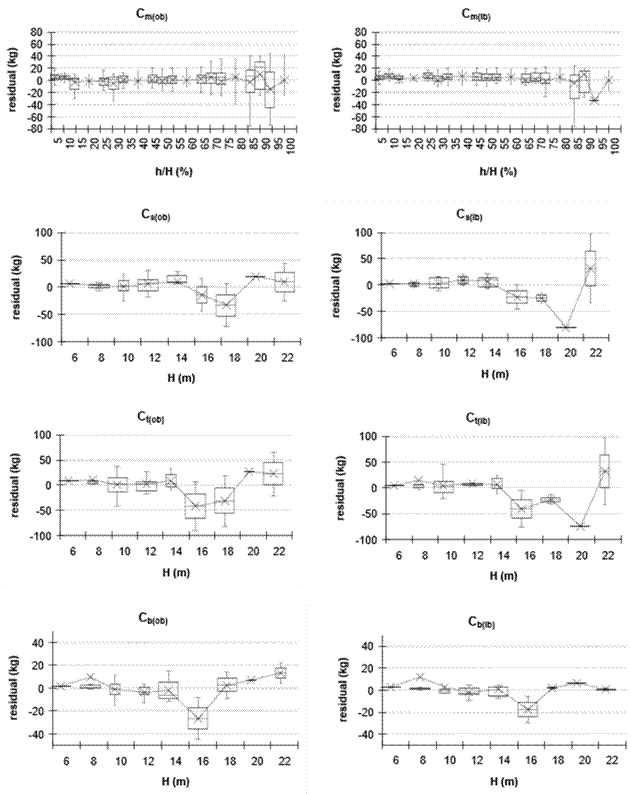
Figure 5. Dispersion of the residuals of merchantable carbon concentration (Cm) with respect to relative height (h/H), and of stem (Cs), total tree (Ct) and branch (Cb) carbon concentrations with respect to total height (H), outside bark (ob) and inside bark (ib).
Table 5 shows the variances-covariances and correlations matrix for some of the CS variables. Because the green weight, biomass and carbon concentration were scaled from the volume, it was logical that the residuals were correlated. The correlation coefficient of the W md and W mg errors was 1.00, as it was also for C m with W mg and W md ; this pattern was observed for the residuals outside- and inside-bark. A similar trend was found for the stem green weight, biomass and carbon concentration equations. This implies that as the residuals of one equation vary, they also do systematically for the other equation. This correlation is not important, as it is possible that the stem profile predictions will improve if the bolt correlation is reasonably traced (Fang et al., 2000). The taper-merchantable volume correlation (0.13 and 0.02 outside- and inside-bark, respectively) presented the same pattern for green weight, biomass and carbon concentration. In addition, the data comply with the factor pointed out by Williams and Reich (1997); that is, they were representative of the study area and not taken in the cutting areas, which are considered mature trees.
Table 5 Variances-covariances and correlations matrix of the residuals of the compatible taper, volume, green weight, biomass and carbon concentration system of Quercus sideroxyla.
| Variables | outside-bark | inside-bark | |||||||||
| d | Vm | Wmg | Wmd | Cm | D | Vm | Wmg | Wmd | Cm | ||
| outside-bark | d | 7.17 | 0.02 | 11.76 | 5.18 | 2.33 | 4.40 | 0.01 | 3.64 | 1.60 | 0.75 |
| Vm | 0.13 | 0.01 | 3.40 | 1.50 | 0.73 | 0.03 | 0.01 | 2.52 | 1.11 | 0.55 | |
| Wmg | 0.06 | 0.82 | 5 402 | 2 379 | 1 199 | 45.93 | 1.99 | 3 309 | 1 457 | 730.91 | |
| Wmd | 0.06 | 0.82 | 1.00 | 1 048 | 528.46 | 20.23 | 0.88 | 1 457.78 | 642.04 | 321.91 | |
| Cm | 0.05 | 0.80 | 1.00 | 1.00 | 267.03 | 10.19 | 0.43 | 724.84 | 319.24 | 160.18 | |
| inside-bark | d | 0.50 | 0.16 | 0.19 | 0.19 | 0.19 | 10.78 | 0.06 | 85.38 | 37.60 | 18.82 |
| Vm | 0.02 | 0.40 | 0.39 | 0.39 | 0.38 | 0.26 | 0.01 | 6.76 | 2.98 | 1.49 | |
| Wmg | 0.01 | 0.45 | 0.46 | 0.46 | 0.45 | 0.26 | 0.98 | 9 775 | 4 305 | 2 151.99 | |
| Wmd | 0.01 | 0.45 | 0.46 | 0.46 | 0.45 | 0.26 | 0.98 | 1.00 | 1896 | 947.79 | |
| Cm | 0.01 | 0.45 | 0.46 | 0.46 | 0.45 | 0.26 | 0.98 | 1.00 | 1.00 | 473.74 | |
| Vs | Vt | Wsg | Wsd | Cs | Vs | Vt | Wsg | Wsd | Cs | ||
| outside-bark | Vs | 0.01 | 0.01 | 6.04 | 2.66 | 1.31 | 0.01 | 0.01 | 3.95 | 1.74 | 0.87 |
| Vt | 0.85 | 0.01 | 7.55 | 3.32 | 1.66 | 0.00 | 0.01 | 5.66 | 2.49 | 1.25 | |
| Wsg | 0.87 | 0.85 | 9 234 | 4 066 | 2 045 | 4.19 | 4.44 | 5 906 | 2 601 | 1 300 | |
| Wsd | 0.87 | 0.85 | 1.00 | 1791 | 900 | 1.85 | 1.96 | 2 601 | 1 145 | 572.82 | |
| Cs | 0.85 | 0.84 | 1.00 | 1.00 | 453.69 | 0.93 | 0.99 | 1 306 | 575.25 | 287.62 | |
| inside-bark | Vs | 0.48 | 0.54 | 0.54 | 0.54 | 0.54 | 0.01 | 0.01 | 9.27 | 4.08 | 2.04 |
| Vt | 0.41 | 0.67 | 0.48 | 0.48 | 0.48 | 0.89 | 0.01 | 9.75 | 4.29 | 2.15 | |
| Wsg | 0.48 | 0.54 | 0.54 | 0.54 | 0.54 | 1.00 | 0.89 | 13 075 | 5 758 | 2 879 | |
| Wsd | 0.48 | 0.54 | 0.54 | 0.54 | 0.54 | 1.00 | 0.89 | 1.00 | 2 536 | 1 333 | |
| Cs | 0.48 | 0.54 | 0.54 | 0.54 | 0.54 | 1.00 | 0.89 | 1.00 | 1.00 | 634.09 | |
The variances are presented on the diagonal of the matrices, and the covariances and correlation coefficients are at the top and bottom of the diagonal, respectively. d = taper, Vm = merchantable volume, Vs = stem volume, Vt = total tree volume, Wmg = merchantable green weight, Wsg = stem green weight, Wsd = stem biomass, Cm = merchantable carbon concentration, Cs = stem carbon concentration.
Although the results of fitting the CS equations showed efficient statistics assuming constant density, a function to model density would improve the results. This is because wood density values increase from the base of the tree to the top, as well as from the center of the stem to the outside of the bark (Calegario, Gregoire, da Silva, Tomazello, & Alves, 2017). In addition, young trees with narrow growth rings have higher wood density than old trees (Pajtík, Konôpka, & Lukac, 2008). The use of a linear or quadratic wood density function may improve predictive accuracy; however, improvements may only be marginal and can considerably increase the complexity of the system (Jiang & Brooks, 2008).
Conclusions
A compatible taper, volume, green weight, dry biomass and carbon concentration system for the species Q. sideroxyla was generated, with the inclusion of wood density. Fitting statistics showed that outside- and inside-bark equations efficiently estimate variables in the stem, total tree and branch components. Variables can be estimated at a desired upper-diameter or upper-height. Although density was not modeled as a function of merchantable height in the compatible system, the results demonstrate that the equations are consistent. These can be used to carry out timber and carbon inventories, for forest management and planning objectives or for environmental services in the measurement and monitoring of carbon sequestration. In addition, the compatible system allows estimating the biomass expansion factors.











 texto en
texto en 


