Introducción

Uno de los efectos ópticos más interesantes que se han estudiado en los últimos años es aquel relacionado con la refracción negativa. Este efecto anómalo lo predijo ^{Veselago (1968)} hace 40 años. Por otro lado, las propiedades ópticas de materiales se han estudiado ampliamente debido a las múltiples aplicaciones tecnológicas. En particular, los materiales artificiales (aquellos que se fabrican) han recibido mucha atención, ya que éstos se pueden diseñar con propiedades ópticas específicas, de tal forma que su aplicación práctica hace que los dispositivos sean más eficientes. Un parámetro importante para la caracterización óptica de un material es el índice de refracción (^{Saleh y Teich, 1991}). El índice de refracción es la respuesta del material a su interacción con la radiación electromagnética (ondas electromagnéticas). En este trabajo explicaremos algunos aspectos de la interacción de la radiación electromagnética con diferentes tipos de materiales.

Debido a que hablaremos sobre la radiación electromagnética es necesario explicar este concepto. La radiación electromagnética también se le llama onda electromagnética. Una onda electromagnética (Ibid) es un ente físico el cual consta de un campo eléctrico y un campo magnético que oscilan en fase y son perpendiculares entre sí y, a su vez, son perpendiculares a la dirección en la cual se propaga la onda.¹ Una onda se caracteriza por una frecuencia angular (ω), la cual está relacionada con la longitud de onda λ de la siguiente manera: ω = 2π • c / λ, donde c es la velocidad de la luz en el espacio vacío. Un ejemplo de onda electromagnética es la luz visible cuya longitud de onda es del orden de 5,000 Å (angstroms), 1Å=10^-10cm. En un medio material de índice de refracción n, la magnitud del vector de propagación de la onda k está relacionada con n y ω por medio de la ecuación k = nω/c. Diferentes medios tienen diferentes índices de refracción y como una consecuencia, la propagación de la radiación electromagnética depende de estos valores. El índice de refracción está relacionado con dos parámetros del material, la permitividad eléctrica (ε) y la permeabilidad magnética (μ). Dependiendo de los valores y signos de estas cantidades, el índice de refracción puede tomar valores positivos, negativos o complejos. En ausencia de efectos de disipación o de absorción, generalmente, el índice de refracción es una cantidad real y positiva. Sin embargo, es posible construir materiales cuyo índice de refracción sea negativo, y, por tanto, las propiedades ópticas se verán modificadas.

Refracción de la luz

Cuando un rayo de luz cruza la interface entre dos materiales distintos, la dirección del haz se modifica, este cambio depende del índice de refracción. El índice de refracción de un medio es una medida que determina la reducción de la velocidad de la luz al propagarse en el material cuando se compara con la velocidad de la luz en el vacío. Este valor nos sirve para calcular el ángulo con que se desvía de su dirección original al atravesar la interface, usando lo que se conoce como la Ley de Snell (^{Saleh y Teich, 1991}). El lector habrá observado cómo un lápiz sumergido parcialmente dentro de un vaso con agua parece no verse recto, esto es, se ve cortado en la frontera entre el aire y el agua. A este fenómeno se le denomina refracción y en todos los materiales conocidos hasta ahora la refracción es positiva.

¿Qué es un metamaterial?

^{Victor Veselago (1968)}, predijo las consecuencias de la interacción de la radiación electromagnética con un material hipotético de índice de refracción negativo, el resultado sería una refracción negativa (véase Fig. 1) contrario a lo observado en todos los materiales existentes. Una pregunta fue si esta asimetría sería posible de alcanzar aunque sea en un material artificial, y se concluyó que, de existir tales materiales, presentarían características notables que modificarían todos los fenómenos electromagnéticos observados hasta la fecha.

Figura 1 Representación esquemática de la refracción positiva y negativa de la radiación electromagnética. 

Como se ha mencionado anteriormente, el índice de refracción puede tener valores negativos, por lo que es necesario considerar que la permitividad eléctrica y la permeabilidad magnética sean también negativos. Surge la pregunta de cómo lograr la construcción de un material con estas características. Después de varios años de investigación, en la actualidad se sabe que aunque menos común que los materiales con índice de refracción positivo, los materiales con permitividad eléctrica y permeabilidad magnética negativas se pueden encontrar en la naturaleza. A frecuencias ópticas hay materiales con permitividad eléctrica negativa entre los que se incluyen los metales como la plata, el oro y el aluminio, mientras que materiales con permeabilidad magnética negativa, incluyen materiales con resonancia ferromagnética o sistemas anti-ferromagnéticos. Aunque estas dos propiedades son viables, la refracción negativa no se había observado. La razón por la que no se había observado este efecto es que la permitividad eléctrica negativa es posible encontrarla para algunos materiales en frecuencias muy altas, como son frecuencias ópticas (luz visible) para metales, o frecuencias del infrarrojo para semiconductores y aislantes. Por otra parte, los sistemas de resonancia magnética ocurren a baja frecuencia, es decir, los fenómenos electrónicos y magnéticos no ocurren en el mismo rango de frecuencia de manera natural. Sin embargo, el desarrollo de la tecnología de materiales ha logrado diseñar sistemas donde simultáneamente estos dos parámetros sean negativos, de ello se hablará más adelante.

En materiales con índice de refracción negativo (^{Veselago, 1968}; ^{Pendry y Smith, 2004}), conocidos como materiales izquierdos o metamateriales, los rayos de luz incidentes se curvan hacia “el lado contrario” a lo esperado, en otras palabras, se presenta la refracción negativa de la radiación electromagnética. Para ilustrar este fenómeno, en la Figura 2 se muestra la comparación entre la refracción positiva (vaso de la izquierda) y la refracción negativa (vaso de la derecha). En el lado izquierdo se presenta la situación habitual, se trata de un líquido con índice de refracción positivo, en donde se observa que la barra introducida se curva en la misma dirección en la que se encuentra en el aire, sólo con un ángulo distinto (refracción positiva). A la derecha se muestra la situación cuando el líquido tiene un índice de refracción negativo. Lo que se aprecia es que la barra aparece como rota, inclinada en dirección opuesta a la parte que está en el aire. Además, hay otras cosas más sutiles e interesantes. En primer lugar, la parte inferior de la interfaz líquido-aire es visible, ya que los rayos emitidos hacia abajo son refractados negativamente hacia arriba. Por el mismo motivo, la parte superior del fondo del vaso no puede verse, ya que los rayos emitidos hacia arriba son refractados hacia abajo.

Crédito: G. Dolling et al.,. - (c) 2006 Optical Society of America.

Figura 2 Se muestra la comparación entre la refracción positiva (vaso de la izquierda) y la refracción negativa (vaso de la derecha). En la refracción positiva el líquido tiene índice de refracción positivo, mientras que en la refracción negativa, el índice de refracción del líquido es negativo. 

Efecto Doppler

A la variación de la frecuencia de una onda provocada por el movimiento del observador o de la fuente se le conoce como Efecto Doppler (^{Ramkrishna, 2005}). Para ilustrar esto, considérese a una persona que se encuentra cerca de un equipo de sonido, el ruido producido por éste lo escuchará con una cierta frecuencia. Si la persona camina hacia el equipo, detectará una frecuencia más alta, es decir, escuchará el sonido más agudo y si se aleja del equipo, detectará una frecuencia menor, esto es, lo escuchará más grave. Este efecto también puede observarse para ondas de luz, por ejemplo, si una persona camina hacia un semáforo que tiene luz roja observará un color de mayor frecuencia, esto es, si la persona pudiese viajar a velocidades comparables con las de la luz podría llegar a ver el semáforo en verde aun cuando estuviese en rojo. El corrimiento de la frecuencia para fuentes u observadores en movimiento, del que habla el Efecto Doppler, depende de la velocidad con la que se propagan las ondas y de los objetos en movimiento relativo. Si las ondas se mueven en un material izquierdo, la velocidad quedará en sentido inverso y esto llevará a que la frecuencia calculada por el observador en movimiento se obtenga de manera inversa a la que ocurre en el caso de los materiales de índice de refracción positivo, esto es si una persona pudiese viajar a velocidades cercanas a las de la luz, un semáforo en verde lo podría ver en rojo.

¿Cómo construir un metamaterial?

En la actualidad es posible construir metamateriales en diferentes geometrías. A continuación describiremos algunos arreglos geométricos que permiten lograr metamateriales. Además comentaremos sobre sistemas fotónicos que tienen refracción negativa.

Arreglos con base en circuitos

Se forma un conjunto de elementos ordenados periódicamente y que están diseñados para responder a la acción de un campo electromagnético. El tamaño y la separación deben ser mucho menor que la longitud de onda de la radiación electromagnética de interés para el estudio. Esto permitirá que la radiación incidente interaccione con el material artificial como si éste fuera homogéneo. De esta manera se puede reemplazar el sistema compuesto por un material continuo con parámetros “ε” y “μ”, los cuales son la permitividad eléctrica y la permeabilidad magnética, respectivamente.

El primer sistema que presentamos en este reporte es la propuesta realizada por ^{Pendry y Smith (2004)}. Aquí consideraremos un material artificial que se construye con un arreglo de alambres, los cuales se cortan periódicamente. Usando este sistema se puede escribir la fórmula de la función dieléctrica que corresponde al modelo de Drude-Lorentz (Ibid; ^{Gupta, 2004}), y de donde se obtiene que para cierto rango de frecuencias ésta es negativa. Por otro lado, la respuesta magnética de un conductor se puede obtener a partir de corrientes inducidas a través de alambres en circuitos cerrados, con lo que se puede lograr una respuesta magnética intensa, la cual permite producir una permeabilidad magnética negativa (^{Pendry y Smith, 2004}). Las estructuras que Pendry y colaboradores propusieron se forman de circuitos conductores que contienen brechas. Estos sistemas se pueden visualizar como circuitos en miniatura. Recordemos que un campo magnético dependiente del tiempo induce una fuerza electromotriz en el plano del elemento produciendo una corriente en el conductor. La brecha en el circuito genera una capacitancia en el plano del circuito y da lugar a una resonancia en la frecuencia, la cual se debe a la geometría del elemento. Este circuito, que puede tener diferentes formas, con una resonancia (de manera equivalente a un átomo magnético) permite el diseño de un metamaterial. El medio con alambres conductores y con anillos representa los elementos básicos (uno eléctrico y otro magnético) para un sistema con respuesta de metamaterial.

Crédito de la Figura: Cálculo de la fuerza de Casimir entre placas paralelas de cristales fotónicos construidos de metamateriales, Tesis de Maestría, Irina S. Solís Mora, FCFM-BUAP, Puebla, México (2006).

Figura 3 Se muestran esquemas de dos materiales artificiales: En a) se presenta un metamaterial construido de alambres que se cortan periódicamente para generar resonancias y circuitos con resonancias. El sistema es similar al propuesto por Pendry et al., que permite generar permitividad eléctrica y permeabilidad magnética negativas. La parte b) está dedicada a un sistema fotónico bidimensional. El índice de refracción es positivo, pero el arreglo geométrico permite la refracción negativa.  

Cristales fotónicos

Es posible producir refracción negativa en un cristal fotónico que consiste de un arreglo periódico de dos materiales como en los metamateriales, pero que tienen índice de refracción positivo y velocidad de grupo positivo (^{Li et al., 2003}). Una estructura en la cual ha sido posible encontrar estas propiedades, es una red cuadrada de huecos en un medio dieléctrico. El medio tiene una permitividad eléctrica grande comparada con la de los huecos, que tienen un radio de r = 0.35a, donde a es la magnitud de los lados de los cuadrados de la red. Los estudios consideran la propagación de luz con una polarización donde el campo eléctrico es transversal (^{Luo et al., 2002}), en este caso es posible tener refracción negativa en dos regiones de frecuencia. Una región de baja frecuencia, con límites superior ω_u = 0.198 x 2πc/a e inferior ω₁ = 0.186 x 2πc/a, donde el índice de refracción es positivo, y una región de alta frecuencia, que está en las vecindades de ω = 0.287 x 2πc/a, donde el índice de refracción es negativo. Si consideramos ahora que los huecos en el dieléctrico tienen un radio mayor, por ejemplo r = 0.45a, es posible lograr refracción negativa para la propagación de la radiación electromagnética con polarización tal que el campo magnético es transversal (Ibid). En este caso la región de frecuencias está en las vecindades de ω = 0.20 x 2πc/a.

Existe una propuesta (^{Cubukcu, 2003}) alternativa para la construcción de estos arreglos y que generan las propiedades de un metamaterial, ésta consiste en un arreglo cuadrado de varillas de dieléctrico en aire. Las varillas tienen una permitividad eléctrica también altamente contrastante con el vacío, el diámetro que se ha elegido es de 2r = 3.15 mm, y longitud l = 15cm. Este sistema sirve para estudiar la propagación de radiación electromagnética con polarización tal que el campo magnético es transversal. Como en los casos anteriores para estos parámetros, en la región de frecuencias de 13.10 a 15.44 GHz se obtiene refracción negativa para la propagación de la radiación electromagnética.

Crédito de la imagen: C. Luo et al., Phys. Rev. B.

Figura 4 Se muestra la fuente (source) y la imagen (image) en la refracción negativa en un arreglo geométrico de un sistema bidimensional fotónico. 

Sistemas composito

En un trabajo reciente, ^{Podolskiy et al. (2005)}, publicaron una propuesta para construir un metamaterial. El sistema considera un diseño no convencional, el cual no requiere que la permitividad dieléctrica y la permeabilidad magnética sean simultáneamente negativas para tener un material de mano izquierda. El medio es no magnético y la respuesta dieléctrica se representa a través de un tensor, en otras palabras, se tiene anisotropía dieléctrica, esto es, la respuesta del material varía dependiendo de la dirección en la que incide la radiación. Para ser precisos, el sistema es un composito que se forma con inclusiones anisotrópicas en un medio dieléctrico isotrópico. El modelo requiere que las inclusiones sean esferoidales y que estén distribuidas uniformemente a través del dieléctrico. Un ejemplo de este medio material es el composito que se forma de un 10% de nano-esferoides de (carburo de silicio) SiC que se encuentren inmersas en una matriz de quartz. Esto permite usar un laser de dióxido de carbono (CO₂) con una longitud de onda de 12um para los estudios de la propagación de la radiación electromagnética con una polarización donde el campo magnético es transversal. Además, en el trabajo de ^{Podolskiy et al. (2005)}, se ha propuesto otro composito que se forma de inclusiones isotrópicas (esféricas) en un medio dieléctrico. Este material se puede obtener mediante el depósito de un dieléctrico seguido por un depósito aleatorio de inclusiones o mediante la deformación del composito con una distribución isotrópica de inclusiones.

Se han realizado estudios de la propagación de radiación electromagnética en una guía de ondas plana¹¹ construida de un material composito con inclusiones esferoidales, 10% de nanoesferoides de SiC inmersas en una matriz de quartz. Este sistema altamente anisotrópico es no magnético con características de metamaterial, bajo ciertas condiciones. El arreglo geométrico es el siguiente: La guía de ondas es plana y paralela al plano (y, z) de un sistema de coordenadas cartesiano, las superficies están en x = ±d/2. La propagación de las ondas sucede en el plano (y,z). Los resultados de la refracción de la radiación demuestran el comportamiento de refracción negativa, véase Fig. 5. Otro estudio (^{Hernández et al., 2007}) que toma en cuenta a este composito, como un metamaterial, se publicó recientemente. En este trabajo se considera una capa delgada del composito altamente anisotrópico emparedado entre dos dieléctricos isotrópicos. Una representación esquemática de la geometría se muestra en la Figura 6. De acuerdo con el sistema de coordenadas cartesianas, el medio con índice de refracción n₁ ≥ 0 se encuentra ocupando la región z < 0, la capa delgada anisotrópica ocupa el espacio 0 ≤ z ≤ d y tiene una respuesta dieléctrica que es un tensor, y el medio de índice de refracción n₃ ≥ 0 se encuentra en la región del espacio z ≥ d. En este caso, la propagación sucede en la dirección z. Los estudios suponen que la radiación electromagnética viaja de izquierda a derecha, el vector de propagación de la luz incidente en el sistema hace un ángulo θ con la línea normal a la interface entre el medio isotrópico de índice n₁ y la capa anisotrópica de composito, tal y como se muestra en la Figura 6. La radiación se refleja y refracta en la interface entre los medios 1 y 2, así como en la interface entre los medios 2 y 3.

Crédito de la Figura: V. A. Podolskiy, and E.E. Narimanov, Phys. Rev. B

Figura 5 Presentamos en a) una guía de ondas de espesor d que confina la radiación en la diercción x y permite la propagación en la dirección z del sistema de coordenadas cartesiano. En b) se muestra la refracción negativa para dos valores de la permitividad eléctrica. En c) se dibuja el módulo del campo eléctrico para los casos presentados en b): la línea azul corresponde a la parte superior de b) y la línea roja a la parte inferior de b). 

Figura 6 Representación esquemática de la geometría para inducir un metamaterial. La película delgada de espesor d, construida de un composito anisotrópico se encuentra emparedada entre dos medios isotrópicos, uno de índice de refracción n₁ (medio de la izquierda) y otro de índice de refracción n₃. La radiación electromagnética incide sobre el sistema con un ángulo de incidencia q. 

Tomando en cuenta los parámetros usados en ^{Hernández et al., 2007}, para la propagación de luz con polarización donde el campo magnético es transversal, existen tres regiones de ángulos de incidencia que producen diferentes espectros de reflexión. Consideremos que la capa delgada del material altamente anisotrópico está emparedado entre dos medios isotrópicos, 1 y 3, y supongamos que el medio de la izquierda tiene índice de refracción n₁ =2 y que el medio de la derecha tiene índice de refracción n₃ = 1, las tres regiones de ángulos de incidencia están delimitadas por los siguientes valores: I) 0 ≤ θ ≤ 30º, II) 30 ≤ 0 ≤ 39.23º, y III) 39.23º ≤ θ. Reportamos los resultados obtenidos para la reflexión de la luz para tres espesores diferentes de la capa anisotrópica. (Para la región II d=2.5, 3, 4, y para la región III, d=5, 10, 15. Aquí d=1 corresponde a 12um). En la región I, la radiación incidente sufre reflexión total, la radiación electromagnética no se puede propagar a través de la capa anisotrópica. En la región II, la reflexión tiene un mínimo para cada valor del espesor de la película. El mínimo sucede a un ángulo de incidencia de aproximadamente 31.85⁰. Estos mínimos indican que la radiación incidente se acopla al modo de superficie de la capa anisotrópica. Finalmente, para la región III la reflexión tiene una serie de mínimos. Los mínimos indican que un número entero de medias longitudes de onda de la radiación caben en la capa dieléctrica. El número de mínimos depende del espesor d de la película, de tal forma que aumenta con el espesor. Es importante hacer notar que en la región III, del ángulo de incidencia, es donde la película delgada tiene refracción negativa. En otras palabras, es en esta región donde se induce un metamaterial, cuando el ángulo de incidencia de la radiación satisface la condición de pertenecer a la región III.

Materiales invisibles

Los metamateriales, debido a sus propiedades de refracción negativa, podrían usarse para hacer invisibles los objetos. Hasta hace poco, solamente se había podido fabricar metamateriales que funcionaban en la región infrarroja y de microondas del espectro de radiación electromagnética, o que eran invisibles vistos desde un solo ángulo. Para fabricar un metamaterial es necesario que sus dimensiones internas sean mucho menores que la longitud de onda de la radiación electromagnética incidente. En el caso de la luz visible está en el rango de 400 a 700 nanómetros. Por tanto, para tener materiales invisibles, su estructura debe ser muy pequeña, en la nanoescala. Recientemente, el grupo del profesor Xiang Zhang, de la Universidad de California en Berkeley ha creado dos metamateriales con índice de refracción negativo para todos los ángulos de incidencia de la luz visible. En un primer trabajo publicado en la revista Science (^{Zhang et al., 2008A}), los investigadores crearon una nueva clase de material embebiendo nanoalambres de plata de 60 nanómetros de anchura en una lámina de óxido de aluminio de un grosor de una centésima de milímetro. Los nanoalambres estaban alineados unos con otros y colocados perpendicularmente a la lámina de óxido. Se reportó refracción negativa para todos los ángulos de incidencia en la región visible. En el segundo trabajo, publicado en la revista Nature (^{Zhang et al., 2008B}), los investigadores fabricaron una estructura tridimensional parecida a una red de pescar y formada por 21 capas alternadas de fluoruro de plata y de magnesio de 30 y 50 nm de grosor respectivamente. Perforaron hoyos rectangulares de 565nm×265nm, separados 800 nanómetros unos de otros y creando la apariencia de la red. Los autores demostraron que el material poseía un índice de refracción negativo para frecuencias ópticas (luz visible). Estos materiales tridimensionales podrían tener muchas otras aplicaciones tales como la mejora en el funcionamiento de antenas de comunicación, al reducir el “ruido” de las ondas electromagnéticas o en superlentes, los cuales describiremos en la siguiente sección.

Figura 7 En esta figura se muestran resultados de la reflexión de la radiación electromagnética que incide sobre el sistema emparedado, descrito en la Figura 6. El panel de la izquierda representa la reflexión en la región II y el panel de la derecha, corresponde a la región III del ángulo de incidencia, como se describe en el texto. En cada caso se consideran tres espesores de la película. En ambos paneles se indican los espesores y en el panel de la derecha se muestra θc2, que es el límite entre las regiones II y III. 

Figura 8 En esta figura se dibuja la refracción negativa en una película delgada de espesor d, de un metamaterial (índice de refracción igual a -1). El objeto está en la parte izquierda de la película a una distancia d/2 y la imagen se obtiene en la parte derecha a una distancia d/2. 

Superlentes

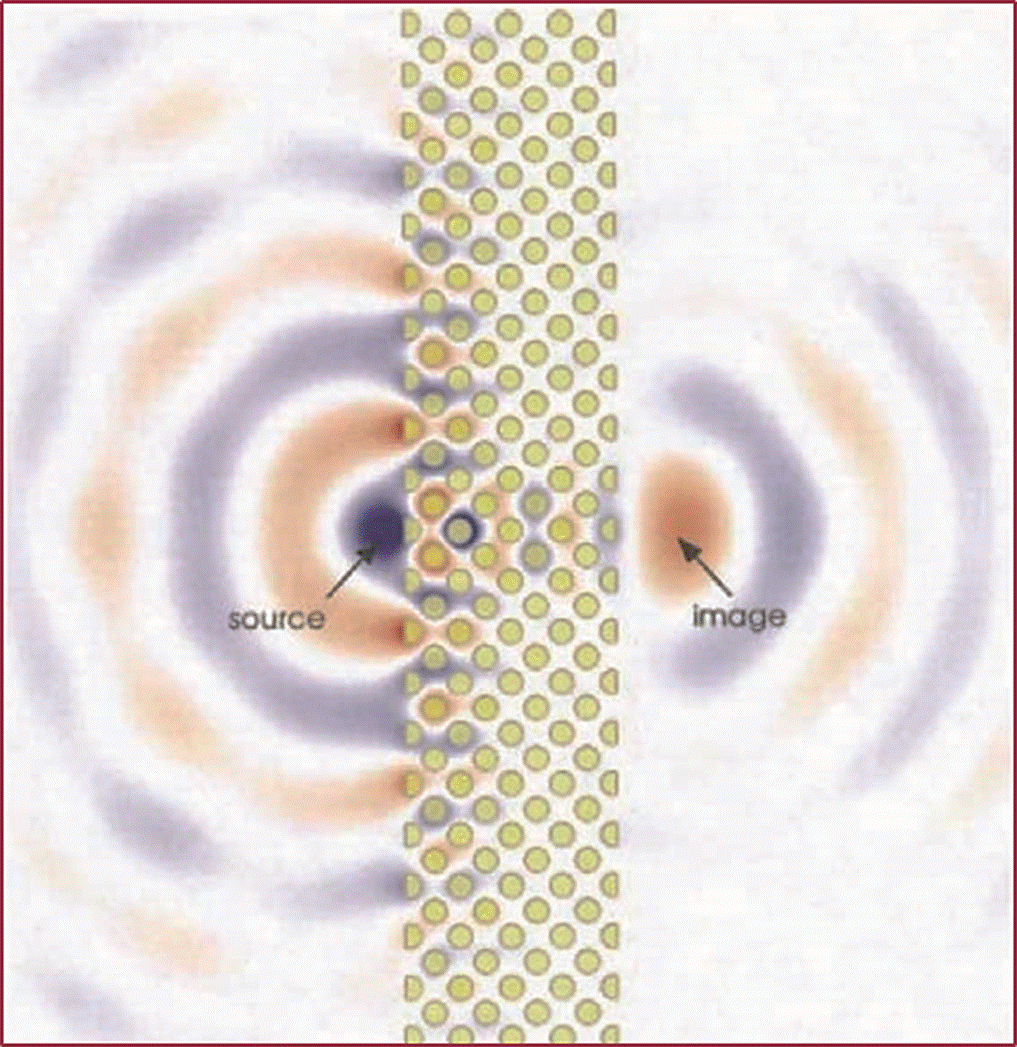
El propósito de esta sección es ilustrar otro ejemplo de aplicación práctica de los materiales con refracción negativa. Una de las consecuencias de la refracción negativa es que puedan enfocar objetos de manera similar a las lentes convencionales. La diferencia importante es que estos nuevos materiales tienen superficies planas (^{Ramkrishna, 2005}; ^{Pendry y Smith, 2004}), en contraste a las lentes convencionales que requieren de una superficie curva para poder enfocar rayos que provienen del infinito. En los metamateriales, un rayo proveniente de una fuente ubicada a una distancia d/2 en el lado izquierdo, puede enfocarse en el lado derecho a una distancia d/2, con el solo hecho de atravesar un material izquierdo de un ancho d, como se ilustra con los rayos dibujados en la Figura 3. Esto hace útiles a estos materiales, ya que no se requieren grandes dimensiones para mejorar la resolución de una lente. Por otra parte, estos materiales permiten superar la barrera, que imponen los instrumentos ópticos, a la que se le denomina límite de la difracción. La difracción es un fenómeno que ocurre cuando la radiación electromagnética, en su trayectoria, encuentra un obstáculo, ésta se dispersa y se curva. Se produce en todo tipo de ondas: ondas sonoras, ondas en la superficie de un fluido y ondas electromagnéticas. La difracción sólo se observa si el tamaño del obstáculo que encuentran las ondas es del mismo orden que la longitud de onda de la radiación. La distorsión de la luz por la difracción produce una borrosidad que limita la capacidad de aumento útil de un microscopio, o de un telescopio. Así, los detalles menores de media milésima de milímetro no pueden verse en la mayoría de los microscopios ópticos. Las razones de esta resolución limitada son la difracción y la incapacidad de los dispositivos de imagen convencionales de enfocar componentes. Cabe señalar que en los metamateriales no existe corrimiento de fase de una onda que viaja del punto fuente al punto imagen, en contraste con las correcciones de fase que deben hacerse en las lentes convencionales.

Conclusiones

Hemos presentado aspectos relacionados con la refracción negativa de la radiación electromagnética en materiales artificiales. Se han presentado los sistemas y mostrado las condiciones bajo las cuales esta refracción anómala puede suceder. Un tipo de sistemas se llaman metamateriales, en los cuales el índice de refracción efectivo es negativo, acompañado de una velocidad de fase negativa. Otros tipos de materiales son aquellos donde los índices de refracción de los componentes son positivos y la velocidad de grupo de la radicación electromagnética es positiva. También se ha discutido la posible aplicación en la industria de la óptica. Concretamente se ha comentado que los materiales que presentan refracción negativa se pueden emplear en la fabricación de lentes con superficies planas. Es importante hacer notar que para que los metamateriales funcionen en el espectro visible de la radiación, las componentes de los sistemas deben tener dimensiones en la nanoescala.