Introducción
La difracción de rayos x (DRX) se ha utilizado para analizar la composición de suelos e identificar minerales, aleaciones, metales, materiales catalíticos, ferroeléctricos y luminiscentes entre otros. Este tipo de análisis se ha incorporado al estudio de materiales en el área de nanociencias, debido a que la información que arroja un difractograma ayuda a determinar la estructura cristalina y la composición de un material, e incluso, a partir de un difractograma se pueden calcular los tamaños de grano. El difractograma está formado por reflexiones (picos) que corresponden a las distancias de dimensiones nanométricas entre familias de planos de átomos. Las dimensiones se tornan relevantes en las nanociencias cuando aparece una nueva propiedad en los materiales asociada a esa dimensión y esto es objeto de estudio en el Centro de Nanociencias y Nanotecnología de la Universidad Nacional Autónoma de México. Este trabajo está enfocado a ejemplos en los que la DRX ha sido crucial para resolver cuestiones en sistemas nanométricos especialmente en America Latina.
Historia
En 1895, Wilhelm Conrad Roentgen descubrió los rayos x. Al principio, los rayos x tuvieron aplicaciones en el campo de la medicina. La noticia más antigua sobre los rayos x en la República mexicana data del 19 de febrero de 1896 y fue publicada en el diario El Estandarte de San Luis Potosí. En la Ciudad de México, la primera radiografía aplicada al diagnóstico quirúrgico de la que se tiene noticia fue realizada por el Dr. Tobías Núñez, el 29 de octubre de 1896 (Stoopen, 1997).
En 1913, William Henry Bragg y su hijo William Lorentz establecieron las bases de la ciencia conocida como roentgencristalografía o radiocristalografía, la cual estudia la estructura de los cristales usando difracción de rayos x (Cordero, 2000a). La DRX llegó a México treinta y siete años después de las investigaciones de Bragg, con los trabajos pioneros de Carlos Graef Fernández, Octavio Cano Corona y Francisco José Fabregat Guinchard (Cordero, 2000b).
En el Centro de Nanociencias y Nanotecnología (CNyN), la Difracción de rayos x (DRX) dio inicio propiamente con la llegada del difractómetro Philips modelo X’Pert (Figura 1a) en marzo de 1996, en el entonces Laboratorio de Física de Ensenada del Instituto de Física de la UNAM. Los primeros análisis fueron efectuados en la alteración de vidrio volcánico de la península de Baja California (Aparicio et al., 1996 y Avalos et al., 1996). En 1997, se inició formalmente el análisis de muestras por estudiantes e investigadores del ahora CNyN. En promedio se analizan anualmente mil muestras de polvo o películas delgadas; se han identificado fases en catalizadores, materiales ferroeléctricos y minerales arcillosos, entre otros.
Laboratorio de difracción de rayos x del CNyN
El laboratorio de difracción de rayos x alberga un difractómetro Philips modelo X’Pert. El equipo tiene la configuración Bragg-Brentano. Los principales componentes son el tubo de rayos x con ánodo de cobre, con un sistema cerrado de enfriamiento (agua), rejillas, monocromador y el detector. El detector contiene xenón; este tipo de gas es adecuado para detectar la radiación de longitud de onda Cu Ká o longitud de onda larga.
Los rayos x se generan en el tubo, que es una ampolla al vacío que alberga al electrodo positivo (ánodo) y el negativo (cátodo). El cátodo contiene un filamento de tungsteno por donde viajan los electrones, producidos por una diferencia de potencial de 45,000 voltios, que chocan con el blanco de cobre (puede ser de Mo, Fe, Co, etc.). Los electrones que chocan con el blanco producen los rayos x de fondo que atraviesan por una ventana de berilio que, debido a su bajo número atómico, permite el paso de los rayos x (Figura 1b).
La información que se obtiene a partir de los difractogramas permite determinar el sistema cristalino al que pertenece el compuesto así como los parámetros de celda, es decir, la unidad mínima con que se organiza un cristal. Con las intensidades de las reflexiones es posible determinar la distribución de los átomos dentro de la celda (análisis estructural). La geometría de los perfiles en los “picos” o máximos de difracción, permite determinar el tamaño de los cristales.
Usos de la DRX en sistemas nanométricos
Una de las aplicaciones de la DRX en las nanociencias consiste en determinar las estructuras de nuevos compuestos a partir de sus patrones de difracción (Petrick-Casagrande y Castillo-Blanco, 2005) para posteriormente asociar la estructura del compuesto con sus propiedades. Otra aplicación rutinaria es la de identificar la composición de una muestra con base en su estructura cristalina. Esto es común cuando se quiere preparar un compuesto que ya se conoce pero utilizando métodos nuevos, ya sea porque son más baratos, de mayor rendimiento o menos tóxicos.
La identificación se hace a partir del perfil (o patrón) de difracción de rayos x característico para cada compuesto natural o sintético, que es como una huella digital. Los materiales se identifican en la base de datos del International Centre for Diffraction Data (ICDD, 2010) que reporta las condiciones del análisis así como los perfiles de difracción de polvos, las distancias interplanares, las intensidades relativas y los índices de Miller, entre otros.
Una de las contribuciones de la DRX a la identificación de un compuesto al realizar una síntesis nueva fue durante la preparación de nanotubos de carbono (NTC) cuyo catalizador era fibra de acero utilizada para lavar platos y que empleaba benceno como fuente de carbono (Koch, 2007). En este caso, los investigadores se auxiliaron de la DRX para confirmar que estaban obteniendo NTC, ya que en esta síntesis, justo por ser nueva, existía la posibilidad de obtener carbono amorfo (estructura sin orden) y otros compuestos de fierro como impurezas. En los difractogramas que se obtuvieron de muestras colectadas en tres puntos diferentes del reactor, se detectó que aparecieron reflexiones características de grafito (marcadas con un rombo en la Figura 2) que forma las estructuras de NTC. En este caso, la DRX les dio a los investigadores, de manera rápida, indicios de la formación de NTC que posteriormente fue corroborada con imágenes de microscopía electrónica de transmisión.
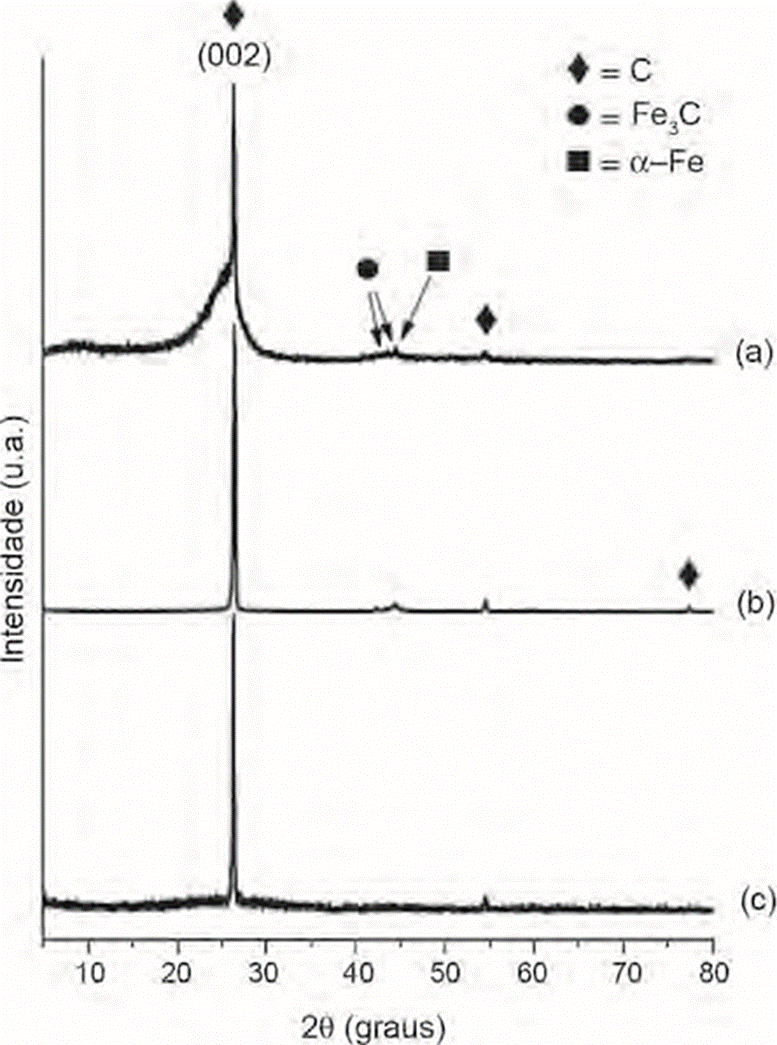
Figura 2 Difractogramas de estructuras de grafito de NTC (rombo) obtenidos (a) al inicio, (b) al centro y (c) a la salida de un reactor tubular. El catalizador fue fibra de acero utilizada para lavar platos. El difractograma ayudó a identificar la presencia de grafito, que es indicio de la formación de nanotubos de carbono (Koch, 2007).
Otra información que dió el difractograma fue que junto con la formación del grafito, también hubo impurezas de fierro y carburo de fierro en poca cantidad. Esto se sabe porque las reflexiones que corresponden a estos compuestos (su huella digital) fueron de baja intensidad (Figura 2a, b)
El caso de los compuestos laminares
La aplicación de la DRX en nuestra área de trabajo se relaciona con el estudio de compuestos laminares. Se les llama así porque están formados por diversas láminas como las que se muestran en la Figura 3.

Figura 3 Estructura laminar del hidróxido de magnesio con distancia interplanar basal (distancia entre láminas) de 0.48 nm, correspondiente al plano 001. (Ficha 9003876 de la Crystallography Open Database, visualizada con Mercury 2.2).
Los compuestos laminares han sido estudiados ampliamente en todo el mundo, debido a que entre las láminas de este material inorgánico se pueden insertar diferentes tipos de moléculas que pueden ser orgánicas. Esto da como resultado la formación de compuestos híbridos con propiedades combinadas de material inorgánico y orgánico. La DRX juega un papel importantísimo, porque la primera reflexión de los difractogramas, que muchas veces es la más intensa, (como las de la Figura 4), corresponde a la distancia existente entre una lámina y otra, denominada espacio interlaminar basal (Figura 3). El espacio interlaminar basal se calcula a partir del difractograma con la ecuación de Bragg:
donde λ es la longitud de onda de los rayos x, que en este caso se trató de una radiación emitida por cobre de 0.15418 nm; D es el valor de la distancia entre los planos y q es el valor del ángulo donde aparece la reflexión (eje x del difractograma).

Figura 4 DRX de hidroxinitrato de zinc (un compuesto laminar) con diferentes dimensiones en el espacio basal. Originalmente están separadas por el ión nitrato y se expanden a medida que aumenta la cadena de los iones orgánicos intercalados: succinato, glutarato y adipato (adaptado de Carbajal, 2004).
Es importante determinar el valor de la distancia basal en los compuestos laminares porque se puede saber de qué forma está orientada una molécula en el espacio interlaminar. Los difractogramas presentados en la Figura 4 corresponden a láminas de hidroxinitrato de zinc, que inicialmente estaban separadas por iones de nitrato situados entre ellas formando un espacio basal de 0.99 nm. Mediante reacciones de intercambio iónico, los iones de nitrato se sustituyeron por iones orgánicos de diferentes tamaños. Nótese que a medida que aumenta el número de carbonos en la cadena del ion (4 carbonos en succinato, 5 en glutarato y 6 en adipato) el espacio basal aumenta de 1.20 a 1.31 y a 1.45 nm.
Los compuestos laminares intercalados con moléculas orgánicas tienen nuevas propiedades y, en algunos casos, se han encontrado resultados sorprendentes como la detección de distintos comportamientos magnéticos cuando se modifica la distancia entre las láminas en fracciones de nanómetros.
El ejemplo específico se observó en láminas formadas por hidróxido de cobalto. Entre las láminas se introdujeron iones de diversos tamaños para separarlas. El resultado fue que a cada distancia de separación hubo un cambio en la susceptibilidad magnética. Hubo fenómenos de transición antiferromagnética a paramagnética (TN) cuando la separación de las láminas era de 0.47 a 0.69 nm, y transiciones ferromagnéticas a paramagnéticas (TC) con separaciones de 0.92 a 2.54 nm (Tabla 1) manifestadas a diferentes temperaturas. La difracción de rayos ayudó en este caso a demostrar que una separación nanométrica entre las láminas induce grandes cambios en las propiedades magnéticas.
Tabla 1 Láminas de hidróxido de cobalto separadas por distintos aniones a diferentes temperaturas de ordenamiento determinadas por ensayos de susceptibilidad magnética.
| Compuesto | Separación de las láminas (nm) | Temperatura (I) de ordenamiento (K) |
|---|---|---|
| Co(OH)2 | 0.47 | TN = 10.0 |
| Co2(OH)3(NO3) | 0.69 | TN = 9.8 |
| Co7(OH)12(NO3)2·3H2O | 0.92 | TC = 23.4 |
| Co2(OH)3(acetato) | 0.94 | TC = 13.0 |
| Co2(OH)3(acetato) ·H2O | 1.28 | TC = 18.0 |
| Co2(OH)3(C12H25SO4) ·2H2O | 2.54 | TC = 7.9 |
*Adaptada de Laget et al. (1996).
Determinación de tamaños de partículas (ecuación de Scherrer)
Además de que un difractograma nos ayuda a identificar composiciones y a medir las dimensiones de las estructuras cristalinas, también es posible utilizarlo para determinar el tamaño de las partículas que generan las reflexiones del difractograma.
La ecuación de Scherrer relaciona la forma de la reflexión de un plano de átomos y la dimensión del cristal en la dirección de ese plano. La ecuación es (Barbosa et al., 2005):
donde: D es tamaño del cristal en la dirección evaluada; λ es la longitud de onda de la radiación de rayos x; θ es el ángulo de difracción de la reflexión evaluada; k es una constante que depende de la forma del cristal, en el caso de partículas esféricas se considera k = 0.9; y β es el ancho que presenta la reflexión a la mitad de la altura, conocida como FWHM por sus siglas en inglés.
Retomando como ejemplo el compuesto laminar intercalado con ácido glutárico de la Figura 4, para calcular la dimensión del cristal a lo largo del eje basal (dirección de apilamiento de las láminas), se traza la altura de la reflexión basal (línea azul en la Figura 5) y se mide el ancho (β) a esa altura (línea roja). Con estos datos, y sabiendo que la longitud de onda del equipo que utilizamos es una emisión de cobre Kα = 0.15404 nm, el resultado nos indica que este cristal tiene una dimensión de 14.0 nm.
Comparación del tamaño de partícula calculado con la ecuación de Scherrer e imágenes de microscopía electrónica de transmisión
La eficiencia de algunos catalizadores (compuestos o materiales que aceleran una reacción química) depende del tamaño de las partículas y por lo tanto es necesario conocer sus dimensiones. Un ejemplo lo tenemos en la preparación de catalizadores de platino dispersados en carbono que se utilizan en celdas de combustible. Una vez que los autores obtuvieron el catalizador por medio de diversas condiciones de síntesis, calcularon los tamaños de los cristales a partir del perfil de DRX, utilizando la ecuación de Scherrer que arrojó resultados de tamaños entre 2.8 a 9.3 nm (Salgado, 2003). Los datos utilizados para el cálculo se obtuvieron a partir de la reflexión más intensa del difractograma (plano (111)) mostrado en la Figura 6a.

Figura 6 (a) Perfiles de DRX de diversas muestras de platino y (b) las imágenes de microscopía electrónica de barrido que ratifican los tamaños de las nanopartículas (zonas oscuras) calculados con la ecuación de Scherrer (Salgado, 2003).
Los resultados tuvieron buena correlación con las dimensiones que mostraron las imágenes de microscopía electrónica de transmisión (Figura 6b), demostrando que la estimación de tamaños de partícula por medio de un difractograma es confiable.
Tamaño de partículas y cristalinidad relativa
Podemos mencionar otro ejemplo en el que, además de estimar los tamaños de partículas nanométricas de un pigmento de zinc y antimonio (Zn7Sb2O12), se utilizó la DRX para determinar variaciones de cristalinidad cuando a la estructura se le introdujo praseodimio en cantidades de 0.01 a 0.10 % (Barbosa et al., 2005). El Zn7Sb2O12 se utiliza como colorante en recubrimietos cerámicos, y la introducción de praseodimio se hizo para buscar nuevas propiedades en este óxido. Para evaluar la calidad de los cristales de las estructuras con praseodimio, se utilizó la DRX para monitorear la cristalinidad relativa por un método simple:
se tomó como referencia el perfil de DRX del compuesto original (Zn7Sb2O12) con más alta cristalinidad, y se comparó con el ensanchamiento y caída de la intensidad de los difractogramas de las muestras dopadas con praseodimio utilizando la siguiente ecuación:
donde: A1 es el área de la reflexión del compuesto de referencia (máxima cristalinidad); y A2 es el área del pico del compuesto dopado con praseodimio. En este trabajo, la DRX ayudó a saber que el grado de cristalinidad, observado por medio de la cristalinidad relativa, no cambió cuando se insertaron los átomos de praseodimio en los cristales de (Zn7Sb2O12), es decir, la calidad de los cristales se mantuvo. Sin embargo, cuando utilizaron la ley de Bragg para verificar las dimensiones de la estructura, observaron que la celda sufrió cambios en sus dimensiones, aumentando de 0.8597 a 0.8613 nm con la inserción de 0.01 y 0.10 % de praseodimio, respectivamente.
Determinación del tamaño de partículas con el modelo Williamson Hall
Hay procesos en que las partículas nanométricas que se obtienen presenten varios defectos en su cristalinidad, como lo sería la preparación de partículas metálicas mediante molienda (D‘Angelo et al., 2006). Las colisiones constantes entre partículas favorecen la formación de defectos, y estos defectos, a su vez, influyen en el ensanchamiento de las reflexiones en un DRX.
En estos casos, el método Williamson-Hall ayuda a separar el ensanchamiento causado por los defectos del cristal y el ensanchamiento debido al tamaño de partícula. La expresión utilizada se basa en la ecuación de Scherrer y se describe como (D‘Angelo et al., 2006):
en donde η es la pendiente que se relaciona con la deformación (defectos) que es inversamente proporcional al tamaño de la partícula (D). Dicha pendiente es extraída al graficar los valores de senq con bcosq como en la gráfica de la Figura 7, que corresponde a muestras de fierro y aluminio de alta pureza, molidas en diversos intervalos de tiempo.
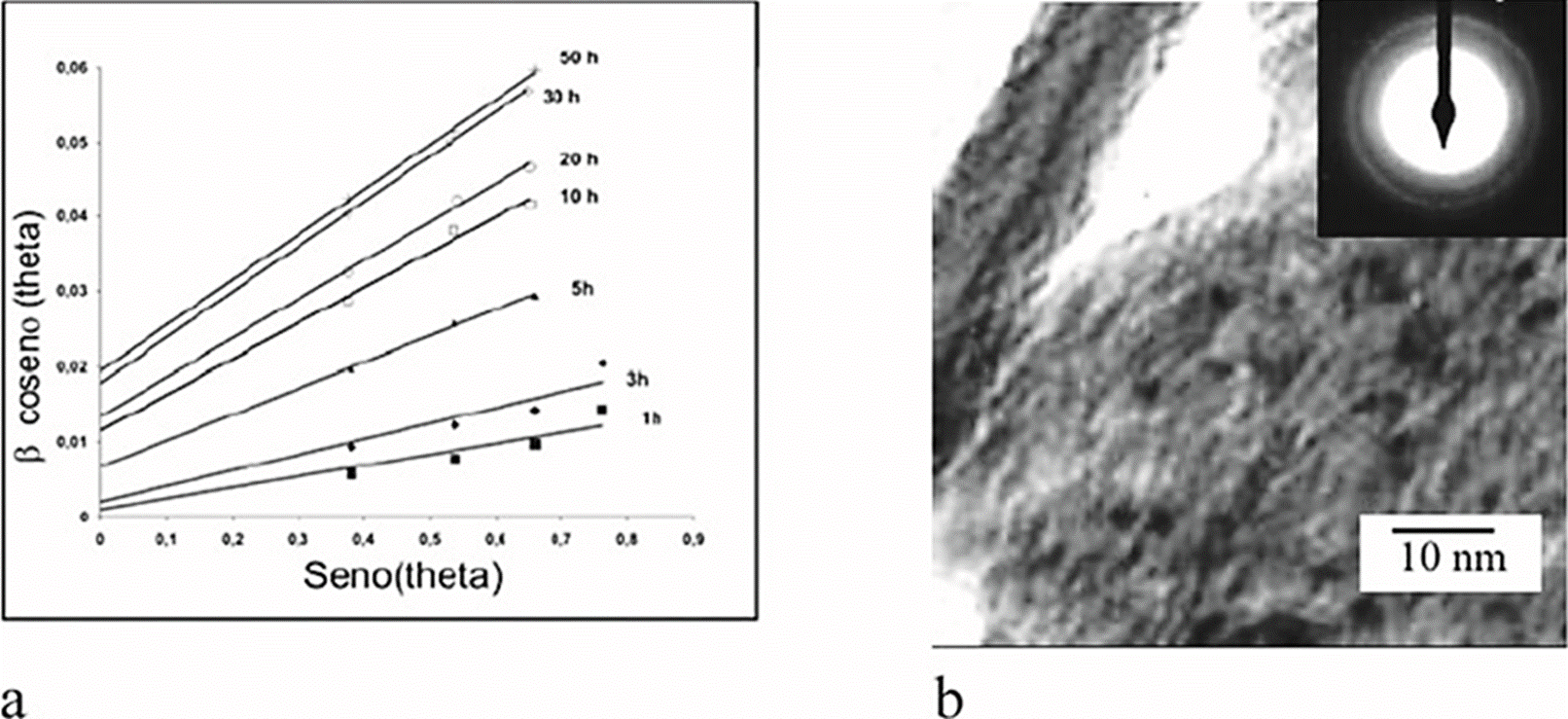
Figura 7 (a) Gráfico que muestra la relación de los cambios de una reflexión (D‘Angelo et al., 2006) y (b) las imágenes de microscopía electrónica de transmisión que muestran tamaños de partículas de 5 nm y casi 20 nm.
Una vez que se conoce la contribución de los defectos de las partículas en el ensanchamiento de las bandas del difractograma, se puede estimar el tamaño de la partícula. En el caso de la muestra molida por 50 horas, el método de Williamson Hall indicó que las partículas tenían tamaños de 5.9 nm, dato que se confirmó con las imágenes de microscopía electrónica de transmisión (Figura 7). Si la ecuación de Scherrer se hubiera aplicado directamente, el tamaño estimado hubiera sido de 9.97 nm, dado que esta ecuación no es para partículas con grandes cantidades de defectos.
Conclusión
La difracción de rayos x se ha consagrado como una herramienta indispensable para estudios en estado sólido y ciencia de materiales, incluyendo los materiales a escala nanométrica.
Los tipos de información que pueden ser extraídos de un difractograma son: (a) la geometría de la celda y las dimensiones, determinadas a partir de la posición de las reflexiones; (b) la distribución de los átomos dentro de la celda unitaria y las cantidades de los compuestos cuando se trata de mezclas que se estiman tomando en cuenta la intensidad de las reflexiones (picos); (c) analizando la geometría de las reflexiones es posible determinar el tamaño de los cristales; (d) y al hacer un análisis cualitativo se pueden identificar los componentes de una mezcla.
Con los pocos ejemplos citados, en su mayoría de estudios realizados en Latinoamérica, demostramos la utilidad que ha tenido la difracción de rayos X en el estudio de sistemas nanométricos. Esto es sólo una muestra de los incontables trabajos que se desarrollan hoy en día en los que la DRX juega un papel indispensable como herramienta de caracterización cristalográfica de compuestos nanoestructurados.











 nueva página del texto (beta)
nueva página del texto (beta)




