INTRODUCCIÓN
Ante el decremento en la extracción de petróleo en los campos maduros (Thomas, 2008; Kamari, Nikookar, Sahranavard y Mohammadi 2014; Kaminszczik y López, 2016) se buscan nuevas técnicas de recuperación mejorada de petróleo1 (EOR, por sus siglas en inglés) (Al-Mjeni et al., 2010) para poder acceder a más de dos tercios del petróleo que no se recupera con los métodos convencionales (Lake, Schmidt y Venuto, 1992; Zekri y Jerbi, 2002; Thomas, 2008; Al-Mjeni et al., 2010).
Una de las técnicas EOR es la inyección de químicos ASP, la cual es una alternativa para la extracción del hidrocarburo en yacimientos como Cantarell (Kamari et al., 2014), y en los cuales es posible recuperar al menos 20% del volumen original en sitio (Olajire, 2014). Cantarell, ubicado en la Sonda de Campeche estuvo entre los más productivos a nivel mundial. Específicamente el campo Akal aportó el 95.2% del total extraído en dicho yacimiento, pero en el año 2004 inició su proceso de declinación (Romo, 2015).
Los estudios existentes sobre la valoración económica de la técnica EOR-ASP son escasos, además de que, los aspectos técnicos incluidos en dichos estudios son tratados de manera superficial (Ekern, S.,1988; Galli, Armstrong y Jehl, 1999; Bailey et al., 2004; Armstrong, Galli, Bailey y Couët, 2004).
Una alternativa para la valoración económica son las opciones reales, las cuales han sido utilizadas para valuar inversiones en la que se presentan cambios inesperados en un entorno económico inestable o bajo la presencia de activos intangibles, los cuales no son tomados en cuenta por los métodos de valoración tradicionales (Calle y Tamayo, 2009), como lo es el cálculo del VPN, método que no contempla la flexibilidad estratégica de la empresa para reaccionar ante entornos cambiantes que impactan en el valor de la misma (Milanesi, 2012).
Las opciones reales se basan en el método binomial para cuantificar el valor de la opción, de compra (call) o venta (put) de un activo a un precio y fecha determinada (Cox, Ross y Rubinstein 1979), de tal forma que una inversión bajo un entorno neutral al riesgo requiere de dos pasos. Primero, la proyección binomial del valor del activo, y que en el presente proyecto se refiere a los flujos de ingreso neto esperados. Segundo, la valoración de la opción, lo cual requiere la estimación de las probabilidades neutrales al riesgo2 en que aumenta (p) y baja (1-p) el valor del activo subyacente y que dependen del valor de la volatilidad del activo gemelo, plazo de la valoración y coeficientes de tendencia (Cox, Ross y Rubinstein 1979). De esta manera, las probabilidades neutrales al riesgo no sólo permiten la valoración de la opción sino también la generación de la distribución de los valores finales, es decir, del grado de dispersión o incertidumbre que presentan los flujos de ingreso neto del proyecto (Brambila, 2011).
Como alternativa al modelo binomial, Del Ángel, Márquez y Patiño (1998) y Huang et al. (2017) realizaron la estimación de las probabilidades de un aumento (p) y baja (1-p) en el valor del activo financiero gemelo basados en el método de cadenas de Markov. A diferencia del modelo binomial en el que existe independencia en el cálculo del valor del activo a través del tiempo, el valor de dicho activo en el tiempo futuro depende de su valor actual. Adicionalmente, las probabilidades estimadas con cadenas de Markov no se basan en el principio de neutralidad al riesgo.
El objetivo del presente estudio es evaluar la rentabilidad económica de un proyecto EOR en el que se lleva a cabo la inyección de químicos ASP en el campo Akal en México y cuantificar la flexibilidad e incertidumbre presente en el proyecto. Adicionalmente, se busca mostrar que, desde el punto de vista de las opciones reales, un mayor nivel de dispersión o incertidumbre puede resultar en un mayor valor del activo.
El artículo se divide en 3 secciones: la sección I presenta el marco conceptual en el que se dan a conocer aspectos relevantes de la valoración económica en la industria petrolera, así como del modelo binomial y cadenas de Markov. En la sección II se desarrolla la metodología para llevar a cabo tanto la valoración económica de un proyecto EOR bajo el método tradicional como por el método de opción real europea de abandono. Se continua con el cálculo del nivel de incertidumbre de los flujos de ingreso neto del proyecto. En la sección III se dan a conocer los resultados. Finalmente, se exponen las principales conclusiones.
I. MARCO CONCEPTUAL
Métodos de valoración utilizados en la industria del petróleo
La aplicación de opciones reales en la valoración de proyectos en el sector de hidrocarburos ha demostrado ser un procedimiento útil, tanto para analistas como para inversionistas en la toma de decisiones bajo riesgo financiero e incertidumbre (Ekern, 1988; Armstrong et al., 2004; Bailey et al., 2004; Guimarães, 2004; Suslick, Schiozer y Rodríguez, 2009; Willigers y Bratvold, 2008; Pineda y Sierra 2012). Al respecto, se mencionan algunos estudios en los cuales se han implementado opciones reales de diferente naturaleza, para analizar la opción de desarrollar o no proyectos, así como su ventaja ante diferentes procedimientos numéricos.
Ekern (1988) muestra ejemplos en la industria petrolera, donde sugiere que el enfoque de opciones reales puede dar señales adicionales sobre la rentabilidad en un proyecto de inversión, en contraparte con el análisis de métodos tradicionales. Cortázar y Schwartz (1998) usan el enfoque de opciones reales para determinar el momento óptimo de inversión en un campo no desarrollado de petróleo. Además, utilizan simulación Monte Carlo ya que permite la inclusión de variables aleatorias adicionales, tales como costos y cantidad de reservas. Galli et al. (1999) analizan tres métodos para evaluar proyectos de inversión bajo riesgo en el sector del petróleo: flujo de ingreso neto descontado, árboles de decisión y simulaciones de Monte Carlo. Concluyen que, aunque las simulaciones basadas en el método Monte Carlo modelan la incertidumbre de acuerdo con los valores de los parámetros, ignoran la flexibilidad gerencial. En contraste, los árboles de decisión permiten analizar diferentes estrategias gerenciales, eligiendo la que maximiza el VPN esperado. La desventaja es que este método no genera una proyección acerca de los posibles valores del VPN. Zekri y Jerbi (2002) mediante la proyección del flujo de ingreso neto descontado determinan la rentabilidad de un proyecto EOR en Libia. Los autores indican que el riesgo en un proyecto EOR es básicamente económico. Por una parte, los costos de inversión previos a la extracción son significativos, y por otra, los costos de operación y los correspondientes a la aplicación del químico pueden resultar importantes dado que existe el riesgo de no recuperar la cantidad de petróleo inicialmente estimada. Armstrong et al. (2004) al abordar la cuestión de cómo evaluar la opción de adquirir más información en proyectos petroleros, combina el análisis bayesiano y las opciones reales. Bailey et al. (2004) comparan el método de flujo de ingreso neto descontado con el método de opciones reales. Dichos autores concluyen que mientras el primero es estático e independiente de que se modifiquen las circunstancias, las opciones reales permiten una mayor flexibilidad con respecto a cambios en la ejecución de proyectos a través del tiempo. También Paddock, Siegel y Smith (1988) muestran el valor de las opciones reales en el desarrollo de un campo petrolero en alta mar para maximizar los rendimientos y minimizar las pérdidas. Guimarães (2004) muestra diversos modelos de opciones reales para evaluar inversiones de exploración y producción de petróleo, en específico utiliza el análisis de opciones para determinar si se debe expandir la producción a través de nuevos pozos.
En resumen, la presente sección refiere diferentes procedimientos numéricos, los cuales han sido usados para determinar el VPN, y algunos de ellos tales como árboles de decisión bajo opciones reales y cadenas de Markov, para modelar la incertidumbre presente en un proyecto. Al respecto, mientras se destaca que el método binomial permite cuantificar la flexibilidad presente en un proyecto de inversión (Brandão y Dyer, 2005); se minimiza su importancia en términos de la relación que existe entre la dispersión en los valores obtenidos mediante dicho método y el valor del activo.
Tipos de opciones reales
De acuerdo con Venegas y Aizenstat (2006) la metodología de las opciones reales “es la aplicación de las técnicas de evaluación de opciones financieras a la evaluación de proyectos de inversión” cuando existe la flexibilidad de tomar en el futuro nuevas decisiones relacionadas con dichos proyectos y estrategias. Así bajo la decisión de elegir, entre los flujos de ingreso neto esperados del proyecto (St,) y el valor de remplazo (V), la opción real del proyecto de inversión se puede plantear como una opción de compra o como una opción de venta. Una opción de compra se presenta cuando la empresa tiene el derecho, pero no la obligación, de invertir en la expansión o extensión en el periodo de la inversión, o diferir (retardar) la decisión de continuar la producción del hidrocarburo, es decir, cuando St > V.
En el caso de una opción de venta, ésta se presenta cuando la empresa tiene el derecho, pero no la obligación, de abandonar, reducir o vender una fracción de los activos de la empresa, es decir, cuando St < V.
Cuadro 1 Equivalencia entre la opción real y tipo de opción financiera
| Opción real | Opción de venta | Opción de compra |
|---|---|---|
| Diferimiento | X | |
| Expansión | X | |
| Extensión en tiempo | X | |
| Abandono | X | |
| Reducción | X | |
| Venta de una fracción | X |
Fuente: Elaborado con base en Tamara y Aristizábal (2012).
Adicionalmente, las opciones reales pueden clasificarse con base en el momento en que pueden ser ejercidas, las más comunes son americanas y europeas. Mientras la opción americana puede ejercerse en cualquier momento durante la vida del proyecto, la opción europea sólo puede ejercerse al vencimiento (Bailey et al., 2004; Calle y Tamayo, 2009). En el presente estudio se plantea el desarrollo de una opción real europea de abandono, en el que se propone llevar a cabo la decisión de inversión bajo la técnica EOR-ASP.
Método binomial en la valoración de opciones reales
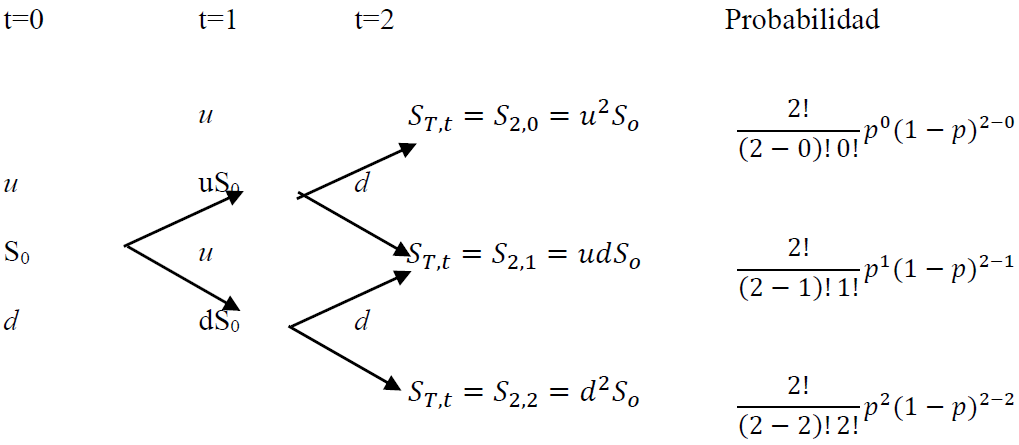
En una inversión en la que se requiere tomar una decisión estratégica bajo incertidumbre, el método binomial de valoración de opciones propuesto por Cox et al. (1979) plantea una relación entre el valor del activo subyacente, su volatilidad y el valor de la opción (valor esperado de los beneficios actualizados). El primer paso en la valoración de una opción real es la proyección binomial. La variable a simular parte de un valor inicial S0 y evoluciona mediante un proceso multiplicativo, el cual toma dos valores posibles (coeficientes de tendencia), al alza (u) y a la baja (d) y los cuales dependen entre otras variables de la volatilidad estimada (σ) (véase ecuaciones 1 y 2).
Bajo una opción real, los flujos de ingreso neto (S0) se modelan mediante la volatilidad estimada de un activo gemelo y que en el presente estudio refiere al rendimiento del precio en dólares de la mezcla mexicana de petróleo. Si el rendimiento del precio del activo sube en t=1, S0 se calcula como uS0, y si baja se calcula como dS0. Los coeficientes de tendencia u, d se determinan con base en las siguientes formulas:
Donde 𝑒 es el exponencial, ∆𝑡 es el incremento en un periodo de tiempo, 𝜎 es la volatilidad anualizada de los rendimientos diarios y 𝑟 la tasa de descuento. Adicionalmente se debe de cumplir la condición de 𝑢 > 𝑟 > 𝑑, de otra manera, existen oportunidades de hacer operaciones de arbitraje en las que se obtenga un beneficio (Cox et al., 1979).
De manera similar uS0 y dS0 pueden aumentar o disminuir a medida que se dan los incrementos de tiempo y en el que el resultado (aumento o disminución de Sn) en cada nodo subsiguiente es independiente del resultado presente en el nodo anterior, generando un modelo binomial expandido en t períodos. Cada uno de los valores St generados en t, nuevamente tendrán la opción de subir o bajar, situación que se repetirá hasta alcanzar ST,t en el nodo final (figura 1).
El segundo paso es el cálculo del valor de la opción. Con base en los valores de u, d y la tasa de descuento (r) se determina la probabilidad neutral al riesgo3 de que el valor del activo S0 suba (p) o baje (1-p). Las probabilidades neutrales al riesgo p y (1-p) se expresan de la siguiente manera (Bailey et al., 2004):
Para determinar el valor de la inversión bajo la opción real, se consideran los valores de los últimos nodos (ST,t) del modelo binomial expandido y se elige el valor máximo entre ST,t y V, es decir, CT = max(ST,t , V). Posteriormente, basado en el proceso de inducción hacia atrás el valor del nodo precedente (CT-1,t) se calcula como el valor actualizado obtenido de los valores maximizados de dos nodos ponderados por las probabilidades neutrales al riesgo. Dicho procedimiento se aplica hasta llegar al nodo inicial C0 lo que permite crear un nuevo modelo binomial (Brambila, 2011).
Adicionalmente en cada nodo final de la proyección binomial, cada valor ST,t tiene asociado la probabilidad de que se presente, y la cual, se calcula mediante la ecuación (5) (Brambila, 2011).
Donde t es el número de nodos con probabilidad p, 𝑇 es el total de periodos, 𝑝 es la probabilidad neutral al riesgo de subir y 𝛽 denota la probabilidad binomial de ST,t presente en el nodo final.
Método de cadenas de Markov
Hernández-Lerma y Venegas-Martínez (2012, p. 375) afirman que, “Existen muchos sistemas económicos y financieros en los que los hechos futuros tienen asociada una distribución de probabilidad que depende sólo del presente, en cuyo caso podría ser idóneo modelarlos con cadenas de Markov”.
El método de cadenas de Markov ha sido utilizado en diversos estudios con el objetivo de llevar a cabo la valoración de activos. Huang et al. (2017) mediante cadenas de Markov desarrollan un modelo de pronósticos para analizar la variación del precio de un activo. Al respecto, una cadena regular es usada para obtener información de lo que sucederá a largo plazo, y adicionalmente saber si la distribución de probabilidades de los estados tiende a estabilizarse a través del tiempo de una manera eficiente. Eriksson y Pistorius (2015) desarrollan un algoritmo para la función de valor de una opción americana bajo cadenas de Markov en tiempo continuo. El algoritmo proporciona un método eficiente y preciso para su valoración, así como el cálculo del límite óptimo. Simonato (2011) propone un enfoque numérico en el contexto log-normal salto difusión, para lo cual utiliza una matriz de transición, que permite desarrollar una cadena de Markov y evaluar los precios de las opciones. Hoek y Elliott (2012)) basados en la teoría de fijación de precios de activos utilizan una función de descuento estocástica. Esta función permite modelar la incertidumbre en una economía al usar cadenas de Markov.
Una cadena de Markov proporciona una forma adecuada para analizar las condiciones futuras a través de una matriz de distribución de probabilidades (Huang et al., 2017). Rincón (2012) menciona que es un proceso estocástico en tiempo discreto,{𝑋𝑡: 𝑡 = 0,1, . . . }, con espacio de estados discretos que satisface la propiedad que para cualquier entero 𝑡 ≥ 0, y para cualesquiera estados 𝑋0, … , 𝑋𝑡+1, se cumple:
𝑝(𝑋𝑡+1|𝑋0, … , 𝑋𝑡) = 𝑝(𝑋𝑡+1|𝑋𝑡) (6)
Si al tiempo 𝑡 + 1, se le considera como un tiempo futuro, al tiempo 𝑡, como el presente y a los tiempos 0, 1, … , 𝑡 − 1, como el pasado, entonces la condición establece que la distribución de la probabilidad del estado del proceso al tiempo futuro 𝑡 + 1, depende únicamente del estado del proceso al tiempo 𝑡, y no de los estados en los tiempos pasados 0, 1, … , 𝑡 − 1. Una vez que las probabilidades calculadas no dependan del tiempo en que se considere, t, se tiene una cadena homogénea; es decir, una matriz de transición, en el que las probabilidades son las mismas en cada estado (Huang et al., 2017). Dado que dichas probabilidades se mantienen sin cambios en cada estado, es posible introducirlas en la fórmula de la distribución binomial con el objeto de realizar la simulación de los flujos de ingreso neto del proyecto (S0), conocer su correspondiente distribución de probabilidades y determinar el valor de la opción.
II. METODOLOGÍA
En el presente estudio se lleva a cabo la valoración económica de un proyecto EOR- ASP del Campo Akal en México tanto por el método tradicional como por el método de una opción real europea de abandono. Los resultados obtenidos son comparados con el objeto de determinar el valor de la opción real europea de abandono.
Posteriormente, se determina el nivel de incertidumbre de los flujos de ingreso neto. A través del modelo binomial se lleva a cabo la proyección de dichos flujos y lo cual requiere del cálculo de las probabilidades4 tanto de un aumento (p) como de una disminución (1-p) del valor del activo subyacente. El modelo binomial por un lado toma como insumo la volatilidad histórica de los rendimientos de los precios del petróleo, y por otra, las probabilidades calculadas con cadenas de Markov. Adicionalmente se llevan a cabo dos pruebas estadísticas. La prueba no paramétrica de Kolmogorov-Smirnov permite mostrar sí la distribución de probabilidad estimada se distribuye como una función log-normal. La prueba de Wald-Wolfowitz (prueba rachas) permite conocer si las observaciones sucesivas repetidas de un mismo evento son independientes estadísticamente, y de esta manera, determinar si los rendimientos del precio del petróleo deben de ser modelados como una variable independiente o dependiente.
Determinación del VPN
El VPN del proyecto EOR-ASP se calcula mediante el método de valoración tradicional (Hernández del Valle y Martínez, 2007):
Donde V es el costo de inversión, St representa el flujo de ingreso neto esperado del proyecto en el año t (donde t va de 0 hasta n), y r es la tasa de descuento.
La sumatoria de los flujos de ingreso neto descontados (S0) se obtiene de la diferencia entre los ingresos y costos proyectados en cada periodo t, variables que se estiman a partir del volumen por recuperar acumulado de petróleo (VRA), uno de los puntos técnicos más importantes del proyecto (Dandekar, 2006; Al-Mjeni et al., 2010). El VRA se modela con el factor de recuperación final por año (FR), que es la relación existente entre la extracción acumulada de aceite y el volumen original en sitio a condiciones atmosféricas (Langenkamp, 2006). Dado que FR es una estimación, sus valores resultantes se comparan con los resultados obtenidos mediante el análisis de las propiedades reales del yacimiento (Álvarez, Ortuño, González y Pérez, 2013; Suslick et al., 2009); es decir, mediante pruebas en laboratorio de muestras de roca del campo Akal, en el que se analizan: porosidad, permeabilidad, saturación inicial de aceite y profundidad (Kamari et al., 2014). De esta manera, el VRA y el FR son modelados con las siguientes fórmulas:
Donde VRA depende del volumen original en sitio (Vtb) y que corresponde a las reservas probadas5. FR depende del factor de recuperación máximo (FR max ), de la velocidad del FR max (λ), y del volumen poroso inyectado de químico ASP por año6 (Vol poroso_iny ). A su vez, Volporoso_iny depende tanto del volumen inyectado de químico ASP (Vol i ny ) como de Vtb y 365 corresponde a los días del año calendario. Los valores técnicos requeridos para el cálculo del VRA son los siguientes:
Cuadro 2 Valores para el cálculo del VRA
| Voliny | Volumen inyectado de químico ASP | 6 mmb / día |
| Vtb | Volumen original en sitio | 30,685 mmb |
| FRmax | Factor de recuperación máximo del volumen original en sitio | 20 % |
| λ | Velocidad del FRmax | 2.1 |
| FR | Factor de recuperación | Variable* |
| Volporoso_iny | volumen poroso inyectado de químico ASP | 7%/año |
*El porcentaje de dicho factor se incrementa de manera decreciente con el transcurso de los periodos hasta alcanzar un valor del 20 % en un plazo máximo de treinta y nueve años.
Fuente: Elaboración propia con base en información de CNH (2018).
Con base en las variables anteriores, el máximo VRA es de 6,137 mmb. Los ingresos proyectados dependeran tanto del VRA como del precio de petróleo estimado. Para obtener un precio representativo para el año 2017, se siguió la regla emitida por la Securities and Exchange Commission7 (SEC, 2010) según disposiciones referidas en el documento Modernization of Oil and Gas Reporting Requirements. El precio se determina mediante el promedio de la suma de precios del primer día de cada mes. El resultado obtenido fue $46.47 USD/b, el cual se considera al comienzo del proyecto.
Los costos proyectados se explican a partir de aquellos incurridos en la extracción de petróleo y de las operaciones asociadas en la aplicación de fluidos como es requerido en el caso de la técnica EOR-ASP, y para lo cual se tomó como guía el informe Adquisition and Development of Selected Cost Data for Saline Storage and Enhanced Oil Recovery Operations elaborado por Energy Sector Planning and Analysis & National Energy Technology Laboratory (ESPA & NETL, 2014). En dicho informe, se proporcionan recomendaciones para la estimación del costo operacional asociado con el desarrollo continuo de la energía fósil EOR, específicamente para CO2.
El costo de inversión (V) corresponde a los gastos en infraestructura marina y adquisición de ductos, equipos de perforación, mobiliario y oficina, vehículos de transporte y de trabajo, reparaciones mayores, etc. (CNH, 2013).
Probabilidad neutral al riesgo
La probabilidad neutral al riesgo requiere del cálculo previo de la volatilidad (𝜎), tasa de descuento (r) y coeficientes de ascenso (u) y descenso (d) del rendimiento del precio del petróleo. En la presente investigación, la volatilidad (𝜎) se estima a partir de la desviación estándar anualizada de los rendimientos diarios (Hull, 2009) del precio de la mezcla mexicana de petróleo de 2007 a 2017. El valor de la tasa de descuento (r) anual es el mismo que se utiliza en la clasificación de los proyectos de exploración y explotación de hidrocarburos (CNH, 2018). En el caso de los coeficientes de ascenso (u) y descenso (d) del rendimiento del precio del petróleo, se determinan con base en la ecuación (1) y la ecuación (2). Dichas ecuaciones consideran un incremento en el tiempo, ∆𝑡, igual a un año.
Probabilidad con base en el método de cadenas de Markov
Para el establecimiento de una matriz de transición con respecto a la variación de los rendimientos del precio diario del petróleo de la mezcla mexicana, el primer paso es determinar la matriz de distribución, la cual incluye las variaciones de los rendimientos del precio anualizados (Hull, 2009) en dos eventos: ascenso, si se presentó un incremento en el rendimiento con respecto al registrado el día anterior, o descenso si el rendimiento tuvo un decremento con respecto al día anterior. El incremento o decremento en el rendimiento presentado en el estado n se compara con respecto al incremento o decremento presentado en el estado n-1 de tal forma que se conforme una matriz de distribución de eventos de 2 x 2.
Una vez obtenida la matriz de distribución, se calcula la matriz de probabilidad inicial, tanto del ascenso como del descenso en rendimientos. Dichas probabilidades se calculan por cada fila.
Posteriormente, se calcula la matriz de probabilidades de transición, la cual indica la probabilidad de cambio de un estado a otro. Sea i y j, dos estados de una cadena de Markov. A la probabilidad P (Xt= j/ Xt-1= i) se le denota por pij (t-1, t), y representa la probabilidad de transición del estado i en el tiempo t-1, al estado j en el tiempo t. El índice i, se refiere al renglón de la matriz, y el índice j, a la columna. La matriz de probabilidades de transición cumple las siguientes dos propiedades: pij ≥ 0 y Σjpij = 1 (Rincón, 2012); es decir, todas las probabilidades están entre 0 y 1, y la suma de las entradas en cada fila es 1.
A continuación, si la matriz de probabilidades de transición tiende a estabilizarse con el tiempo, permite investigar la condición bajo la cual una cadena de Markov produce un equilibrio, o estado estable. Una distribución de probabilidad π= (π0, π1,…) es estacionaria o invariante para una cadena de Markov con matriz de probabilidades de transición P=(pij) si πj = Σjπipij. En términos matriciales, la distribución de probabilidad π es estacionaria si π = πP. Esta identidad tiene como consecuencia que para cualquier número natural t se cumpla que π = πPt; es decir, π es también una distribución estacionaria para la matriz Pt. Esto significa que, si la variable aleatoria inicial X0 tiene esa distribución π, entonces la distribución Xt también es π ya que P (Xt = j) = Σj πiPij(t) = πj, es decir, esta distribución no cambia con el paso del tiempo y por ello se le llama estacionaria o invariante. En el presente estudio, la matriz de transición será de tamaño 2x2, es decir de dos filas y dos columnas. Cada fila representa un vector con dos entradas, las cuales representan probabilidades que al sumarlas deben ser igual a uno. Adicionalmente, al ser una matriz estacionaria, todas las filas son iguales. Así, el vector fila en la primera entrada mostrará la probabilidad de que el rendimiento suba (p), y en la segunda entrada la probabilidad de que el rendimiento baje (1-p) (Huang et al., 2017).
Modelo Binomial y Distribución de probabilidades del VPN
Al respecto, primero se llevará a cabo la proyección binomial de S0, y posteriormente se realizará la valoración de la opción real. Finalmente se determinará la distribución de probabilidades correspondiente a la proyección binomial, tanto para la volatilidad histórica, como para el método de cadenas de Markov.
Opción real europea de abandono.
A diferencia del método de valoración tradicional en el que se debe de cumplir que los flujos de ingreso neto son mayores a los costos de inversión (V); en el caso de la valoración de la opción real, el valor del activo se modifica debido a la flexibilidad u opcionalidad de tomar una nueva decisión. Así, la decisión de llevar a cabo el proyecto se plantea para cada valor (ST,t) del nodo final del modelo binomial proyectado, de tal forma que si ST,t > V se realiza el proyecto, de otra manera si ST,t < V, la mejor elección para el tomador de decisiones será abandonar el proyecto (Venegas y Aizenstat, 2006). La decisión de abandono se toma previo a la aplicación de la técnica EOR lo que implica una opción real europea.
Con el objetivo de determinar el valor de la opción real, cada valor presente en el nodo final (ST,t) del modelo binomial proyectado se compara con el valor de reemplazo (V) y se elige el valor máximo, es decir, CT = Max (ST,t , V). Posteriormente, basado en el proceso de inducción hacia atrás el valor del nodo precedente (CT-1,t) se calcula como el valor actualizado obtenido de los valores maximizados de dos nodos ponderados por las probabilidades neutrales al riesgo. Dicho procedimiento se aplica hasta llegar al nodo inicial C0 lo que permite crear un nuevo modelo binomial (Brambila, 2011).
Donde C0 es el valor del activo bajo la opción real, p es la probabilidad de ascenso y (1-p) es la probabilidad de descenso. La diferencia entre C0 y V permite obtener el VPN modificado. Finalmente, el valor de la opción resulta de la diferencia entre el
III. RESULTADOS
Determinación del VPN del proyecto
Con base en el método de valoración tradicional el VPN fue de $ 120.157 MMUSD y el cual resultó de la diferencia entre los flujos de ingreso neto (S0) y costos de inversión (V):
VPN = 137.987 - 17.830 = 120.157 MMUSD.
El resultado muestra la viabilidad económica del proyecto dado que cumple con el criterio de S 0 > V (Venegas y Aizenstat, 2006).
Al respecto, dada la tasa decreciente en la recuperación del hidrocarburo con la técnica EOR, los flujos de ingreso neto (S0) se alcanzaron en un plazo de dieciséis años y un VRA de 5,656.91 mmb. Como resultado, la proporción de los costos de operación8 e inyección del químico ASP9) con respecto a los ingresos 10 proyectados se incrementó anualmente al pasar de 0.11 en el primer año al 0.94 en el año dieciséis. Después de dicho año, los ingresos son menores a los costos totales. El costo unitario proyectado fue de $7.14 USD/b para el año 2018.
Zekri y Jerbi (2002) encontraron que el método EOR aplicado en un yacimiento en Libia es rentable11 bajo la aplicación alternativa de dos químicos. El primero, mediante la aplicación de bióxido de carbono que presenta un costo total promedio de $7.14 USD/b, y el segundo mediante la aplicación de hidrocarburo donde el gas natural es el principal insumo y presenta un costo total promedio de $13.06 USD/b. Dichos costos resultaron ser igual y superior (83%) respectivamente al costo total promedio obtenido en el presente estudio.
Alternativamente, en el caso de México, el costo de producción incurrido bajo el proceso de extracción convencional del hidrocarburo para el año 2017 fue de 10.99 USD/b (PEMEX, 2018) mayor (54%) al costo del presente estudio. Olajire (2014) señala que la selección del químico a aplicar como técnica EOR, no sólo depende de las características del yacimiento (tipo de materia orgánica y proceso de maduración del yacimiento), sino también de la disponibilidad de dicho químico, la cantidad requerida a ser aplicada, el costo, el resultado obtenido, y la logística.
En el caso del campo Akal, el método químico ASP resultó ser el más adecuado al permitir la mayor recuperación de petróleo al menor costo posible. En particular, la inyección del químico álcali permite, por una parte, reducir las cantidades de surfactante y polímero y los costos, y por otra, recuperar la mayor cantidad del hidrocarburo. El químico álcali se limita a ser usado en crudos que tienen cantidades suficientes de compuestos ácidos orgánicos siendo el caso del campo Akal (Kamari et al., 2014).
Cuadro 3 Valor presente neto
| Periodo | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Volpor_iny (% | 0.07 | 0.14 | 0.21 | 0.29 | 0.36 | 0.43 | 0.5 | 0.57 | 0.64 | 0.71 | 0.79 | 0.86 | 0.93 | 1 | 1.07 | 1.14 | 1.21 |
| FR(%) | 2.78 | 5.18 | 7.24 | 9.02 | 10.55 | 11.86 | 13 | 13.97 | 14.81 | 15.53 | 16.2 | 16.7 | 17.2 | 17.6 | 17.9 | 18.2 | 18.44 |
| VRA (mmb) | 854 | 1,589 | 2,222 | 2,767 | 3,236 | 3,640 | 3,988 | 4,287 | 4,544 | 4,766 | 4,957 | 5,121 | 5,263 | 5,384 | 5,489 | 5,579 | 5,657 |
| VR anual (mm | 854 | 735 | 633 | 545 | 469 | 404 | 348 | 299 | 258 | 222 | 191 | 164 | 141 | 122 | 105 | 90 | 78 |
| Ingresos (MMU | 36,699 | 34,173 | 29,417 | 25,322 | 21,798 | 18,764 | 16,152 | 13,904 | 11,969 | 10,303 | 8,869 | 7,635 | 6,572 | 5,657 | 4,870 | 4,192 | 3,609 |
| Costos (MMUS | 4,552 | 4,375 | 4,224 | 4,093 | 3,980 | 3,884 | 3,800 | 3,729 | 3,667 | 3,614 | 3,568 | 3,529 | 3,495 | 3,465 | 3,440 | 3,419 | 3,400 |
| FIN (MMUSD) | 35,147 | 29,798 | 25,193 | 21,230 | 17,817 | 14,880 | 12,352 | 10.176 | 8,302 | 6,689 | 5,301 | 4,106 | 3,077 | 2,192 | 1,430 | 773 | 208 |
| VPN(MUSD) | 120.16 |
Fuente: Elaboración propia
Cálculo de las probabilidades
Para la determinación de las probabilidades en que el rendimiento sube (p) y baja (1-p) en el modelo binomial y volatilidad histórica, las variables relevantes consideran los valores siguientes: volatilidad anual (σ = 37.6%), tasa de descuento anual (r = 12%) y periodo en que se incrementan los rendimientos (Δt = 1 año), en un horizonte de 16 periodos. Con dichos valores y utilizando la ecuación (1) y la ecuación (2) se determinaron los valores, tanto para el factor en que el rendimiento sube (u = 1.46), como para el factor en que el rendimiento baja (d = 0.69). Como resultado, las probabilidades estimadas son: p = 0.56 y 1-p = 0.44. Dichas probabilidades cumplen con el principio de valoración neutral al riesgo (Hull, 2009).
Para determinar las probabilidades bajo el método de cadenas de Markov, se procedió al cálculo de la matriz de distribución de los rendimientos (cuadro 4).
Cuadro 4 Matriz de distribución de los rendimientos anualizados
| Estado | t | |||
|---|---|---|---|---|
| Sube | Baja | Total | ||
| t-1 | Sube | 717 | 620 | 1,337 |
| Baja | 620 | 668 | 1,288 | |
| Total | 2,625 | |||
Fuente: Elaboración propia como base a precios diarios en dólares por barril de la mezcla mexicana de petróleo registrados en el periodo 01/Enero/2007 - 31/Diciembre/2017 (BANXICO, 2018)
Posteriormente se calculó la matriz de distribución de probabilidad inicial. Dichas probabilidades se calculan por fila, con base en la matriz mostrada en el cuadro 4, se tiene que la primera fila contiene un total de 1,337 observaciones, por lo que las observaciones registradas en cada evento se dividen entre el total de observaciones registradas en la respectiva fila. Los resultados se muestran en el cuadro 5.
Cuadro 5 Matriz de distribución de probabilidad inicial es de los rendimientos anualizados
| Estado | t | |||
|---|---|---|---|---|
| Sube | Baja | Total | ||
| Sube(p) | 0.54 | 0.46 | 1.00 | |
| t-1 | Baja(1-p) | 0.48 | 0.52 | 1.00 |
Fuente: Elaboración propia.
Después, mediante la matriz de distribución de probabilidad inicial, se calculó la matriz de probabilidad de transición, donde la distribución de la matriz no cambia con el paso del tiempo, de tal forma que la probabilidad pt t-1 ≥ 0, y Σtpt t-1 = 1 (Rincón, 2012). Es decir, todas las probabilidades están entre 0 y 1, y la suma de las entradas en cada fila es igual a 1.
Así, la cadena regular de Markov mostrada en el cuadro 6 después de tres ensayos converge y es estable.
Cuadro 6 Matriz de probabilidad de transición después de tres ensayos
| Estado | t | |||
|---|---|---|---|---|
| Sube | Baja | |||
| (p) | (1-p) | Total | ||
| t-1 | Sube(p) | 0.51 | 0.49 | 1.00 |
| Baja(1-p) | 0.51 | 0.49 | 1.00 | |
Fuente: Elaboración propia.
Los resultados indican que la probabilidad de incrementar y disminuir es p = 51% y 1-p = 49%, respectivamente. En este caso, la probabilidad de subir (p) resultó menor a la obtenida mediante la volatilidad histórica estimada. Con la probabilidad de p y con base en las ecuaciones (1) y (2)se determinaron los valores para los coeficientes u = 1.59, d = 0.63, y volatilidad 𝜎 = 46.6%. Es importante notar que, mientras que en el método binomial se parte del valor de la volatilidad, para posteriormente calcular los valores de los coeficientes u y d, y la probabilidad neutral al riesgo (p); en el método de cadenas de Markov se parte del valor de la probabilidad de transición (p) para calcular los valores de los coeficientes u y d, y la volatilidad mediante el método binomial.
Determinación del VPN mediante el método de valoración de opciones
Mediante el método de valoración de opciones reales se llevó a cabo el cálculo del VPN modificado
Cuadro 7 Valores finales de los flujos de ingreso netos descontados y su respectiva distribución de probabilidades (MMUSD de 2018)
| Probabilidad neutral al riesgo 𝜎 = 37.6% | Probabilidad de cadenas de Markov 𝜎 = 46.6% | ||
|---|---|---|---|
| Valor del nodo final (nodo dieciséis) | Probabilidad | Valor del nodo final (nodo dieciséis) | Probabilidad |
| 9,227.10 | 0.00010 | 38,944.80 | 0.00002 |
| 4,349.87 | 0.00126 | 15,335.11 | 0.00032 |
| 2,050.63 | 0.00736 | 6,038.44 | 0.00231 |
| 966.71 | 0.02667 | 2,377.73 | 0.01036 |
| 455.73 | 0.06729 | 936.27 | 0.03237 |
| 214.84 | 0.12536 | 366.27 | 0.07472 |
| 101.28 | 0.17842 | 145.17 | 0.13173 |
| 47.75 | 0.19787 | 57.16 | 0.18097 |
| 22.51 | 0.17280 | 22.51 | 0.19578 |
| 10.61 | 0.11924 | 8.86 | 0.16735 |
| 5.00 | 0.06480 | 3.49 | 0.11266 |
| 2.36 | 0.02744 | 1.37 | 0.05909 |
| 1.11 | 0.00888 | 0.54 | 0.02369 |
| 0.52 | 0.00212 | 0.21 | 0.00701 |
| 0.25 | 0.00035 | 0.08 | 0.00144 |
| 0.12 | 0.00004 | 0.03 | 0.00019 |
| 0.05 | 0.00000 | 0.01 | 0.00001 |
Fuente: Elaboración propia.
Distribución de probabilidades
Con base en los valores finales de los flujos de ingreso netos descontados y sus respectivas distribuciones de probabilidades se aprecia una mayor dispersión de dichos valores bajo las probabilidades de cadenas de Markov que los valores bajo las probabilidades neutrales al riesgo.
Con los valores finales en cada nodo y su respectiva distribución de probabilidad, se planteó la hipótesis nula (H0) en la que se afirma que dichos valores corresponden a una distribución log-normal. Mediante el programa SAS versión 9.4 se llevó a cabo la prueba estadística Kolmogorov-Smirnov. Los resultados para las distribuciones de probabilidad obtenidas, tanto por medio de la volatilidad histórica, como por el método de cadenas de Markov mostraron un p-value de 0.31 y 0.29 respectivamente, lo cual indica que, en ambos casos, no se rechaza la hipótesis H0 12; es decir, que los datos analizados siguen una distribución log-normal. Lo anterior confirma lo referido por Cox et al. (1979), Bailey et al. (2004) y Milanesi (2012), quienes señalan que en la medida que el número de periodos bajo la proyección binomial se incrementa, la distribución de probabilidades de los rendimientos de un activo tiende a una distribución log-normal (figura 3 ).
La prueba de Wald-Wolfowitz (prueba rachas) plantea la hipótesis nula (H0) de independencia en las observaciones de una variable aleatoria. Esta se llevó a cabo para cada uno de los años del periodo 2007-2017. Los resultados mostraron que, para todos los años del periodo, el estadístico con respecto a las observaciones sucesivas o rachas referentes a la variación del rendimiento del precio se ubicó dentro del intervalo de confianza al 95 por ciento, por lo que no se rechaza la hipótesis nula y se concluye que el método binomial de valoración mediante el uso de la volatilidad histórica es el adecuado para llevar a cabo la simulación de los flujos de ingreso neto.
Es importante señalar que la presente investigación llevó a cabo una valoración del proyecto con un mayor nivel de detalle comparado con investigaciones previas (Galli et al., 1999; Bailey et al., 2004; Armstrong et al., 2004). La estimación del volumen de recuperación acumulado de hidrocarburo implicó determinar previamente variables tales como el coeficiente de volumen poroso inyectado (Volporoso_iny) y el factor de recuperación máximo (FR max ).
CONCLUSIONES
En la presente investigación se llevó a cabo tanto la valoración del proyecto de recuperación mejorada de petróleo en México como la determinación del nivel de incertidumbre de dicho valor bajo la técnica EOR-ASP en el yacimiento Cantarell, específicamente en el campo Akal, que en términos de su producción ha sido uno de los más importantes a nivel mundial.
Con base en el cálculo de los ingresos, los costos de inversión, los costos de operación e inyección del químico, y las estimaciones técnicas sobre recuperación de petróleo se concluye que la aplicación de la técnica EOR mediante el método químico ASP es rentable económicamente. Durante un periodo no mayor a dieciséis años se espera obtener un valor de 120.157 MMUSD.
Al respecto, el método de valoración de opciones reales mostró que debido a la flexibilidad presente en el proyecto el método de valoración de la opción de abandono es el adecuado debido a que permite valorar la alteración en la estrategia operativa propuesta inicialmente. Por lo anterior, un proyecto que valore la opción de abandono valdrá más que aquel que no lo haga.
Finalmente se mostró que el valor de la opción se incrementa a medida que se presenta una mayor dispersión en los valores proyectados mediante el método binomial.











 nueva página del texto (beta)
nueva página del texto (beta)