Introduction
In the current context of slow economic growth experienced by many developed and developing countries and in light of the well-documented set of economic policies undertaken by several East Asian economies leading to the so-called Asian ‘miracle’ (e.g. Amsden, 2001, 2004; Chang, 2006; UNCTAD, 2018), some economists have proposed the use of the nominal exchange rate as a ‘policy variable’ with the purpose of maintaining an undervalued real exchange rate, in order to boost national exports and investment in the tradable sector, which would lift productivity, employment, and economic growth (e.g. Polterovich and Popov, 2003; Rodrik, 2008; Razmi et al., 2009; Bhalla, 2012; Missio et al., 2017).
Given that the exchange rate is a macroeconomic-price capable of having considerable influence on the allocation of resources (mainly financial resources like capital inflows, foreign direct investment, credit, industrial production and inflation), it is likely that the lack of economic growth that many economies have experienced is due, to some extent, to recurring periods of exchange rate overvaluation, which has limited the process of industrial upgrade, created permanent trade deficits and maintained low levels of domestic savings and foreign exchange reserves. This diagnosis could be especially true for African and Latin American economies, which on average, during the years 1981-2010, have been performing worse than in previous periods (1960-1980) and other developing countries (Martínez-Hernández, 2019).
The main objective of this investigation is to make a critical analysis of the effects and consequences of maintaining an undervalued currency upon certain components of aggregate demand of developed and developing countries for the periods 1981-2010 and 1990-2010. Thus, a priori we are not in favor of one specific real exchange rate policy, we are just trying to understand and estimate all the economic impacts, positive or negative of an undervalued currency. In addition, we seek to contribute towards clarifying two absent points in the literature of the relationship between real exchange rate and GDP per capita: 1) we show the existence of different Balassa-Samuelson effects among developed and developing countries, something several empirical studies have overlooked, and 2) we show that for some set of countries there is a non-linear relationship between real GDP per capita and real exchange rate.
On the one hand, our econometrics results confirm what other empirical investigations have previously concluded (Polterovich and Popov, 2003; Rodrik, 2008; Razmi et al., 2009; Bhalla, 2012; Missio et al, 2015). Overall, in the medium-to-long-run an undervalued real exchange rate has had positive effects on economic growth via mainly the trade balance, higher levels of investment, industrial and manufacturing production. Nevertheless, when we disaggregate the main components of aggregate demand for different clusters of developed and developing countries, we found that in general, an undervalued currency has expansionary and contractionary effects in the short-run, specifically via the manufacturing sector, the wage-share and the inflation rate.
On the other hand, due to the foregoing results, we believe that the analysis of the effects of an undervalued currency upon aggregate demand should also be carried out on a case-by-case basis, in order to try to evaluate ‘correctly’ the structural parameters of each economy (types of exports, degree of trade openness, level of foreign indebtedness (public and private), economic performance of the main trade partners, the strength of external demand, etc.) and ‘all the possible channels’ through which a currency depreciation could affect the level of economic activity for a particular economy.
After this introduction, the first section presents a literature review of some researchs that study and analyze theoretically and empirically the economic impacts of holding an undervalue currency upon economic growth. The second section presents our theoretical framework and strategy to analyze the impacts of an undervalue currency on economic growth and certain aggregate demand components in the short and long run. The third section develops our own reformulation of Rodrik’s (2008) exchange rate undervaluation index for the periods 1960-2010, 1960-1980, and 1981-2010. Our main sample considers 96 countries, and it makes distinction between developed and developing countries and considers different blocks of countries (e.g., countries from Africa, Asia, and Latin America).
For our different blocks of countries, drawing on the Dynamic Panel Data methodology, the fourth section estimates for the period 1981-2010 the short and overall ‘long-run’ effects of the undervaluation index upon the trade balance, the ratios of total investment, industrial and manufacturing production with respect to GDP, respectively, the ratio of industrial employment to total employment, and the inflation rate. The fifth section, drawing on the autoregressive distributed lag (hereafter ARDL) approach, for a selection of developed and developing countries for the period 1990-2010, we estimated the ‘short-run’ multiplier effects of the undervaluation index on the main sectoral macroeconomic balances with respect to GDP ((I-S), (X-M), and (G-T)), the ratio of manufacturing production to GDP, the ratio of industrial employment to total employment, the wage-share, and the inflation rate. The last section provides some concluding remarks.
I. Literature review
With regard to the theoretical and empirical analysis of the relationship between changes in the real exchange rate, aggregate demand and economic growth, we basically recognize two camps: 1) those researchers who find a positive and meaningful strong relationship among these economic components and 2) those researchers who pose serious doubts about the alleged economic mechanisms put in place by the undervaluation of the currency, especially in those emerging economies highly globalized productively and financially. We begin analyzing the first group.
According to standard open macroeconomy models, a real depreciation of the exchange rate has an expansionary short-run effect via aggregate demand, if price elasticities satisfy the Marshall-Lerner (M-L) condition (so that the trade balance improves) and there are unemployed resources in the devaluing country (so that output can increase). A real depreciation can also yield benefits on the supply side by increasing the relative price of tradable goods, which creates incentives to shift domestic production towards tradables and demand towards non-tradables, thereby freeing up a greater surplus for exports (Blecker and Razmi, 2008: 87).
Most of the studies that have estimated empirically the effects of the changes of real exchange rate on economic growth focus mainly on the effects of exchange rate depreciations on the external sector, specifically on the performance of the national export sector; that is, in these analyses, an undervalued currency leads to a favorable change in the relative prices of commercial goods, by which tend to raise exports and investment in the tradable sector, employment, wages and economic growth (e.g., Rodrik, 2008; Razmi et al., 2009; Bhalla, 2012).
In the case of Rodrik´s (2008) empirical analysis (1950-2000), he finds that an undervalued exchange rate stimulates economic growth in developing countries via a change in relative prices and an increase in the relative profitability of investment in tradable goods, all of which causes that this sector expands along with the level of exports at the expenses of the non-traded sector. Thus, according to the author, these findings suggest that tradable goods suffer disproportionately from the government or market-failure, so devaluating the currency would act as a second-best fashion to (partially) alleviate the economic cost of these distortions.
Following Rodrik (2008) methodology, Razmi et al., (2009) also found that an undervalued exchange rate spurs economic growth via mainly the size of the external sector and the level of exports; one particular difference with Rodrik´s study is that these authors, in light of their theoretical framework, present empirical evidence that suggest that exchange rate undervaluations tends to promote investment and as a consequence more economic growth but only in developing countries for the period 1950-2004.
In the same vein, Missio et al., (2015) found also that an undervalued currency tends to enhance economic growth and the level of investment for the period 1980-2008; one important difference with the previous two studies is that these authors found a non-linear (quadratic) relationship between economic growth and the estimated index of undervaluation, which suggests that for countries with low economic income per capita, an undervalued currency tends to generate more economic growth but till certain level, surpassing that level an undervalued currency would tend to hinder economic growth. Similar to the two previous studies, all these results only seem to apply to developing countries.
In the case of the developing countries of Latin America, Missio et al., (2015) found that an undervalue currency has a positive (but non-significant) effect upon the income elasticity of the demand for exports and a negative (significant) effect on that of imports. According to these authors, this last result suggests that the hypothesis of elasticities endogenous to the level of the real exchange rate is theoretically supported (more on this below).
Finally, with regard to empirical studies of the first group, we have the study carried out by Bhalla (2012), who found a (statistically significant) nonlinear relationship between the level of the real exchange rate (hereafter RER) and the GDP per capita, but in this case the relationship between both variables trace an S-shape path for a sample of 138 countries for the period 1980-2011, indicating that the growth rate is slow at first, then the growth rate accelerates with a more depreciated currency, and then it slows down once the economy becomes developed. Once this happens, per capita income plateaus, albeit at a very high level with a more appreciated currency.
Now, under a more theoretical approach still with regard to the first group, we analyze three studies, the first one was developed by Bresser-Pereira (2016), who claims that the slowdown in economic growth and the premature deindustrialization observed in several Latin American countries have been caused by the appreciation of their exchange rates, insofar as the appreciation of the currency discourages the production of internationally tradable goods, promotes a productive specialization in primary goods, and reduces the share of manufacturing in GDP.
Therefore, to escape from this premature deindustrialization, this author proposes to maintain a stable undervalued exchange rate, which would tend to increase international competitiveness of the industrial sector, at a cost of lower real wages, but with a higher amount of savings which would support more productive investment and employment. In addition, the author insists on accompanying this competitive exchange rate policy with a long-term government industrial policy encouraging technological research to promote the development of knowledge-intensive industries and high value-added.
If the government is unable to directly subsidize certain industries, especially “infant industries”, then, according to Guzman, Ocampo, and Stiglitz (2017), the maintenance of a competitive and stable exchange rate policy would be able to contribute to diversifying the export structure and hopefully to include more activities with higher technological content. Moreover, in the absence of capital account regulations, central banks could be able to mitigate the pro-cyclical effects of capital inflows through counter-cyclical accumulation of foreign exchange reserves. The cost of maintaining these higher reserves (liquidity) could be reduced via a partial sterilization of excess liquidity (issuing short-and medium-term securities).
Following the foregoing arguments, Missio et al. (2017) claim, through the development of several theoretical models, the existence of an indirect and unidirectional connection of the nominal and RER upon the income elasticities of the demand for exports and imports. Hence, for this theoretical framework, a depreciation of the exchange rate would improve the national exports and discourage the mount of imports, thus relaxing the balance-of-payment-constrained growth. However, the fundamental change would occur when a depreciated currency had a favorable impact on the quality and the diversification of exports (creation of new products), which would be associated to 1) a process of higher productive investment (capital accumulation) in the tradable good sectors and 2) a substantial improvement on the process of innovation and technological change (more R & D) in these same sectors.
Furthermore, on the import demand side, a depreciation of the currency would not only lead to a reduction in the import demand and a higher incentive on domestic production, but also would create a shift on the domestic credit market by encouraging national companies to rely more on domestic credit, on self-financing capacity, and less on external credit. Unlike the previous approaches, this last one recognizes that although the favorable change in relative prices may occur after a depreciation of the currency, this effect is less important than the effect on income elasticities, that is, these elasticities are endogenous and sensible to the level of the RER, therefore, for this approach the depreciation of the currency is more important on its qualitative and quantitative effects upon the upgrading of the national productive structure than on relative prices.
We now focus on analyzing the results of some theoretical and empirical studies that pose serious doubts about the alleged economic mechanisms put in place by the undervaluation of the RER upon economic growth and aggregate demand highlighted by the previous group of studies.
First, according to the standard economic theory, in two cases, a real depreciation of the exchange rate could have a contractionary short-run effect even if the M-L condition is fulfilled: (i) if the devaluation leads to higher domestic prices due to higher costs (mainly imports), which may create a shift in the distribution of income in favor of capital and against labor, by enabling firms to increase price-cost margins (i.e., lower real wages). If capital owners have a higher propensity to save than workers, then overall aggregate demand may fall despite increased exports; and (ii) if the devaluation increases the indebtedness ratio of firms and governments indebted in foreign currency (Diaz-Alejandro, 1963; Krugman and Taylor, 1978; Blecker and Razmi, 2008). Furthermore, if the response of exports (and import substitution) to the change in relatively prices is slow, then the currency depreciation may result in the short run in a worsening of the trade balance, the terms of trade and profits (López and Perrotini, 2006).
Along these lines, Medeiros and Trebat (2016) and Mántey (2017) challenge the two main tenets of the so-called New Developmentalism (Bresser-Pereira, 2016), who ascribe enormous importance to the RER to foment investment and foreign demand. Regarding the first tenet, for Medeiros and Trebat (2016), a depreciation of the currency only redistributes income from wages to industrial profits (through a larger gap between the real exchange rate and unit labor cost). Moreover, for these authors, a strong undervalued currency does not necessarily mean that industrial investment would increase pari passu with the depreciation of the currency as this depreciation could lead to a fall in aggregate consumption due to the inflationary process created with the depreciation, which would prevent larger levels of investment.
This last effect seems to be true theoretically and empirically. Firstly, Ribeiro, McCombie, and Tadeu-Lima (2016) show through a theoretical model à la Thirlwall that, the larger the import component of the economy, the larger the contractionary and inflationary effects of a devaluation on the economy. Secondly, our empirical results in this paper show that the latter effect use to happen for certain economies (see table 3 and 4 below).
About the second tenet, Medeiros and Trebat (2016) question the assumption of the New Developmentalist approach that external demand for industrial production in developing countries always exists and requires only a competitive RER (a small reduction in real wages caused by currency devaluation) to be transformed into “effective demand”. As we know now, the possibility for export-led growth has become more limited in recent years with the fragmentation of world trade characterized by increasing specialization and a high import content of manufactured exports (Medeiros and Trebat, 2016, pp.6). Therefore, even if fully fledged undervalued policies could increase the external demand for some countries, that would not be possible to do so for all developing countries (the so-called fallacy of composition).
For the case of Mántey´s (2017) study, through a classical structuralist theoretical framework and an empirical analysis for a sample of 10 developing countries for the period 1995-2014, she concludes that the RER is not an effective variable to accelerate economic growth for the case of these developing country, since their manufacturing trade balances depend little on relative prices, and more on the way these countries have themselves inserted in the global value chains, this latter being the one that conditions the value added in the local industrial sector.
More specifically, this study finds that exports respond negatively to an exchange rate depreciation, as this has adverse effects on the balance sheets of the economic agents of these countries, basically due to the high indebtedness ratio in foreign currencies. Other three important findings of this empirical study is that 1) the main determinant of manufacturing exports is external demand, 2) there is an absence of causal relationship between the growth of local manufacturing industry and the growth of manufacturing exports, and 3) there is an unidirectional, positive and highly significant causal relationship for the growth rate of manufacturing imports, and in particular from high-technology imports towards the growth of total labor productivity, which implies that a high value of exports have to be imported, thus causing a low multiplier effect on domestic output. Therefore, the author concludes that the hypothesis that premature deindustrialization is caused by real exchange rate appreciation is not valid.
II. Theoretical and strategic framework: Undervaluation and Aggregate Demand in the Short-and-Long Run.
In this section we describe our theoretical framework and the strategy to proceed to estimate the effects of an undervalued currency upon economic growth and aggregate demand.
Firstly, although we agree in general terms with all the foregoing set of policies proposed to foster the diversification and the national component of exports, we also believe that the main emphasis should be put on strengthening national industries with high valued added directly rather than pursuing only an undervalued policy per se, the reason for this is that a one-time depreciation of the currency could only be transformed into a one-time impulse on the national industry without having long-lasting effects. More precisely, even continuous depreciations could end up having negligible effects on industrial production or even worse, with more inflation and (domestic and external) debt and low stimulus on economic activity, especially in developing countries with high current account deficit (see the policies advocated by the second group analyzed above).
Secondly, we believe that the chain of causation emphasized by the first group due to a currency depreciation, although probably correct, it does not describe the full picture associated with exchange rate depreciations. In developing countries, and even in some developed countries, changes in the RER also see important changes in the other components of aggregate demand (aggregate consumption, investment, government expenditure), and even changes in the stance of monetary policy, and thus on credit and economic growth in the short run.
Therefore, we believe that holding an undervalued currency for an extended period could pose serious distributive effects, so we are more inclined towards holding a relatively stable exchange rate subject to changes in relative productivity and real cost of production (relative real unit labor cost) associated with the evolution of direct national industrial and technological policies implemented to foment, diversify and upgrade the key tradable sectors of the economy (see Shaikh, 2016; Martinez-Hernandez, 2017).
Now, regarding our strategy to estimate the impacts of an undervalued currency upon economic growth and aggregate demand components, we begin in the third section re-estimating with a different data set and a slightly different method and technique to that used by Rodrik (2008), our index of undervaluation. In this same section we explain all the details to construct this index and its interesting results.
Afterward, due that all our main variables are stationary series, as they are ratios, we could not make use of the cointegrating panel techniques, so in section fourth we stick to the General Method of Moments (hereafter GMM) technique to obtain the short-run parameters, and then based on those parameters, we were able to estimate the long-run parameters. Finally, in section fifth we made use of the ARDL technique which relies on the two-stage procedure to obtain the short-run multiplier effects of an undervalued currency upon different components of aggregate demand.
III Methodological Aspects of the Relationship between the Real Exchange Rate and GDP Per Capita: Cross-Country Evidence by World Regions through Time.
We begin by reformulating an undervaluation index proposed by Johnson et al. (2007) and Rodrik (2008). This standard methodology for the construction of RER and an undervaluation index uses the Purchasing Power Parity (PPP) conversion factor calculated by the Penn World Tables 7.1, which assumed 2005=100 as the base year or equilibrium reference for prices, thus the deviation of the PPP conversion factor from the market exchange rate (XRAT) is considered a measure of currency misalignment (under/over-valuation).1
Now, building on the work by Johnson, Ostry, and Subramanian (2007), Rodrik (2008) and Bhalla (2012), we computed an index of exchange rate undervaluation in three steps. Firstly, we define the RER in its natural log form as the log of the ratio of the data on exchange rates (XRAT) and Purchasing Power Parity conversion factors (PPP)2.
Where i is an index for countries and t is an index for (1-year) time periods. XRAT and PPP are expressed as national units per U.S. dollar. When ln RER is greater than zero it indicates that the value of the currency is lower (more depreciated) than is indicated by purchasing-power parity (PPP) conversion factor, which is considered the ‘equilibrium’ level of exchange rate, so that the deviation of XRAT from PPP measures the level of currency misalignment (under/over-valuation).
A second step in the construction of the RER is to take into consideration the price difference (due to unequal productivities) between tradable and non-tradable goods among developed and developing countries. That is, according to the Balassa-Samuelson effect, higher productivity in the tradable sector of rich countries pushes up the general level of prices and the RER; while low productivity in the tradable sector of poor countries tends to maintain or lower the general level of prices and more devaluated/depreciated exchange rates. Thus, to discount this income effect over the RER, equation 2 regresses ln RER on the log of per capita GDP (LRGDP_PC):
Where
Figure 1 clearly shows that developed countries follow completely the linear relation first pointed out by Balassa and Samuelson (figure 1 with 25 countries). Meanwhile, the (unadjusted) RER of developing countries (figure 1 with 71 countries) seems to follow a lower rate of change (i.e., overvaluation) as income per capita increases. Moreover, like the Asian and African countries, the developing countries seem to follow a nonlinear relation through time. When we split up our sample of countries (as in figure 1) into two periods (1960-1980 and 1981-2010), the same patterns remained. The upshot is that trying to estimate equation 2 for a combined sample of developed and developing countries might be misleading and biased. Therefore, we basically decided to estimate the adjusted (for income) RER taking up different blocks of countries (as in figure 1) using equation 3 and 3.1.
Equation 3 is like equation 2 but adds a fixed effect for cross-sections to consider different initial conditions and different structural characteristics between countries (Asteriou and Stephen, 2011). Equation 3.1 is like equation 3 but adds an exponential component in the GDP per capita to capture a possible nonlinear relation with the RER.
Where
Using equation 3 and 3.1, we estimated panel (two-way) FE error component models for different periods (1960-1980, 1981-2010, and 1960-2010) and blocks of countries to estimate the parameters beta in equation 3 and 3.1, the Balassa-Samuelson effect (hereafter, B-S effect). Our main sample considers 96 countries (developed and developing), and to consider different stages of development (measured by income per capita) and geographic regions through time, we split up this main sample into different groups of countries as follows: 25 developed countries, 72 developing countries, 35 countries from Africa, 18 countries from Asia, and 20 countries from Latin America. The list of countries for each group and the statistical tests are available upon request to the primary author. Using these more homogeneous groups of countries allow for more precise estimates and reveals interesting differences in the estimated coefficients based on different structural characteristics.
The econometric results of these panel regressions for different time periods and samples are shown in table 1. Our investigation uses annual data4, and a priori, we did not impose any restriction on our econometric panel models (i.e., pooled model, one-way, or two-way FE), that is, we decided which sort of panel model to estimate based on a Chow test (see Baltagi, 2005: 13). Performing a Chow test to our different block of countries and time-periods allowed to consider the heterogeneity between countries and possible changes over time.
Table 1 Balassa-Samuelson effects
| 1960-2010 | 1960-1980 | 1981-2010 | |||||||||
| β1/β3 | Adj-R^2 | FE | β1/β3 | Adj-R^2 | FE | β1/β3 | Adj-R^2 | FE | |||
| All Countries (96) | -0.17 [-34] | 0.64 | 2w | -0.162 [-22.9] | 0.82 | 1w, C | -0.147 [-7.65] | 0.68 | 2w | ||
| Developed (25) | -0.32 [-18] | 0.67 | 1w, C | -0.32 [-7.8] | 0.6 | 1w, P | -0.30 [-4.9] | 0.64 | 1w, C | ||
| Developing (71) | -0.16 [-30] | 0.58 | 2w | -0.11 [-6.3] | 0.82 | 1w, C | -0.15 [-8.3] | 0.53 | 2w | ||
| Africa (35) | -0.23 [-16.4] | 0.6 | 2w | -0.24 [-11.4] | 0.85 | 2w | -0.16 [-6.3] | 0.49 | 2w | ||
| Asia (18) | -0.15 [-15.7] | 0.73 | 2w | -0.16 [-20] | 0.713 | 1w, C | -0.20 [-5] | 0.79 | 2w | ||
| L.A. (20) | -0.31 [-3.6] | 0.10 | 1w, P | -0.20 [-3.7] | 0.93 | 1w, C | -0.39 [-5.2] | 0.53 | 1w, C | ||
Note: The numbers in brackets stand for the t-statistic (based on White cross-section or White period standard errors & covariance). The numbers in parentheses indicate the number of countries in each panel regression.
Source: Own calculations.
Thus, our strategy was to estimate two Chow (F) tests for each block of countries. The first F-test compared a pooled (restricted) model against a cross-section FE (unrestricted) model. The second F-test compared a pooled (restricted) model against a period FE (unrestricted) model. By applying this procedure, we obtained three sets of models: 1) cross-section FE models (1w, C), 2) period FE models (1w, P), and 3) two-way (2w) FE models.
The results on table 1 show that there have been differentiated B-S effects among countries through time, since the estimated
The results on table 1 also show that developed countries have maintained a relatively high but stable B-S effect for the whole period (
Table 1 also shows that except for developed countries, the Latin American countries (hereafter LAC), and the Asian countries (only for the third estimated period, 1981-2010), the other blocks of countries followed a nonlinear relationship through time, which means that at lower levels of GDP per capita, the real exchange rate tends to increase (depreciate) as income per capita increases, but as the level of GDP per capita reaches a higher level, the RER begins to decrease (appreciate) as income per capita continues growing.
Finally, to arrive at our index of undervaluation for each block of countries and period, we take the difference between the actual RER (from equation 1) and the Balassa-Samuelson-adjusted rate (from equation 3 or 3.1) as follows:
Where
Defined in this way, ln UNDERVAL is comparable across countries ‘within’ each block of countries and over time. Whenever ln UNDERVAL exceeds zero, it indicates that the currency in dollar terms is undervalued. When ln UNDERVAL is below zero, the currency is overvalued. Thus, this measure of over-under-valuation is centered at 0.
IV Empirical Results: Undervaluation and some Forces of Economic Growth in the Long-Run, 1981-2010
Based on our own reformulated index of undervaluation for the classification of countries by economic regions defined above, we estimated through the dynamic panel data methodology the effect of an undervalued currency on the trade balance (X_M), the ratio of total investment to GDP (Total Inv_GDP), the ratio of industrial GDP to GDP (Ind GDP_GDP), the ratio of manufacturing GDP to GDP (Manuf GDP_GDP), the ratio of industrial employment to total employment (Ind Emp_Total Emp), and the inflation rate (Inflation). It is important to bear in mind that for each block of countries we estimated a particular undervaluation index, since we identify different B-S effects between developed and developing countries and among developing countries.
To build our econometric models, we start by running panel data unit root tests to our series. These tests suggested that all the series were stationary series for the estimated periods, so this fact prevented us from using the cointegrating panel data technique, which would have allowed us to estimate the long-run effects. Nonetheless, we made use of the properties of the dynamic panel data models to estimate the short and overall long-term effects of undervaluation on our six dependent variables.
We decided to use a dynamic panel data specification as it is possible that the estimated parameters using panel FE models could suffer a problem of endogeneity bias due to a possible problem of contemporaneous simultaneity effect between the dependent variables and the independent variable (
Using the GMM corrects for both problems as it allows the inclusion of a lagged dependent variable, which itself contains the history of the model (through backward interactions), enabling researchers to find overall (long-run) coefficients for the explanatory variable, in our case, the overall long-run effect of LnUnderval. Moreover, the GMM procedure also controls for endogeneity using suitable instrumental variables (see Arellano and Bond, 1991; Baltagi, 2005: Chapter 8; Greene 2008: 468).
The econometric specifications using the GMM approach, and a log-log representation are shown in equation 5 through 10.
Where the subscript it-1 stands for the lag of the dependent variable,
The estimated overall long-term effects from equations 5 through 10 using the GMM are shown in table 2.
Table 2 Undervaluation, trade, investment, manufacturing and industrial production: Overall long-term effects 1981-2010
| Dependent Variable | X_M | Total Investment/GDP | Industrial GDP/GDP | Manufacturing GDP/GDP | |||||||
| Parameter | θ* | lag(s) | ϑ* | lag(s) | τ* | lag(s) | μ* | lag(s) | |||
| All Countries (96) | 0.33 | 0 | 0.22 | 0 | 0.23 | 0 | 0.13 | 0 | |||
| Developed (25) | 0.16 | 0 | 0.19 | 1 | 0.68 | 0 | 0.77 | 1 | |||
| Developing (71) | 0.36 | 0 | 0.24 | 0 | 0.11 | 1 | 0.11 | 0 | |||
| Africa (35) | 0.36 | 0 | 0.44 | 0 | 0.39 | 0 | 0.14 | 0 | |||
| Asia (18) | 0.39 | 0 | 0.17 | 2 | 0.39 | 0 | 0.19 | 0 | |||
| L.A. (20) | 0.54 | 0 | 0.28 | 4 | 0.20 | 1 | 0.24 | 0 | |||
Note: The numbers in parentheses indicate the number of countries in each panel regression.
Source: Own calculations.
Table 2 displays the overall long-term elasticities of undervaluation upon our first four key macroeconomic variables. Thus, although these results show different elasticities, all these are positive. Here we can only say that all of these parameters are statistical significant different from zero at the 5% of statistical significance and that the probability of the Sargan-Hansen test of over-identifying restrictions (J-statistic) and the second-order autocorrelation in the residual test (AR(2)) are higher than the 5%, which suggest the use of valid instruments under the null hypothesis that the over-identifying restrictions are valid and that the number of instruments are appropriate, respectively (Arellano and Bond, 1991; Stock and Watson, 2015).
Regarding the trade balance (X_M), the LAC show the largest positive long-term elasticity to an increase in undervaluation. The developed countries reported the lowest long-term positive elasticity to an increase in undervaluation. In general, the results for the trade balance for all the blocks of countries show that an increase in the undervaluation of the currency tends to improve the trade balance by reducing imports, and to a certain degree, by increasing exports.
For the case of the ratio of total investment to GDP (Total Inv_GDP), the African countries show the highest elasticity, which means that African countries tend to attract more investment when the currency weakens. The Asian and developed countries showed the lowest elasticity to an increase in undervaluation. The developing countries as a whole and the sample of LAC countries reported almost similar positive elasticities on Total Inv_GDP due to an increase in undervaluation.
Another interesting result from table 2 not shown thus far by other empirical investigations is the fact that despite the long de-industrialization process that many developed countries have been experienced for at least over the last thirty years, the undervaluation of the real exchange rate seems to improve the industrial and manufacturing production of these developed countries as their long-term elasticity reported by table 2 turned out to be positive and the highest, which means that these productive sectors are sensitive to retain or expand national industrial and manufacturing production when there are changes in the value of the currency (see figure 2 and 3).
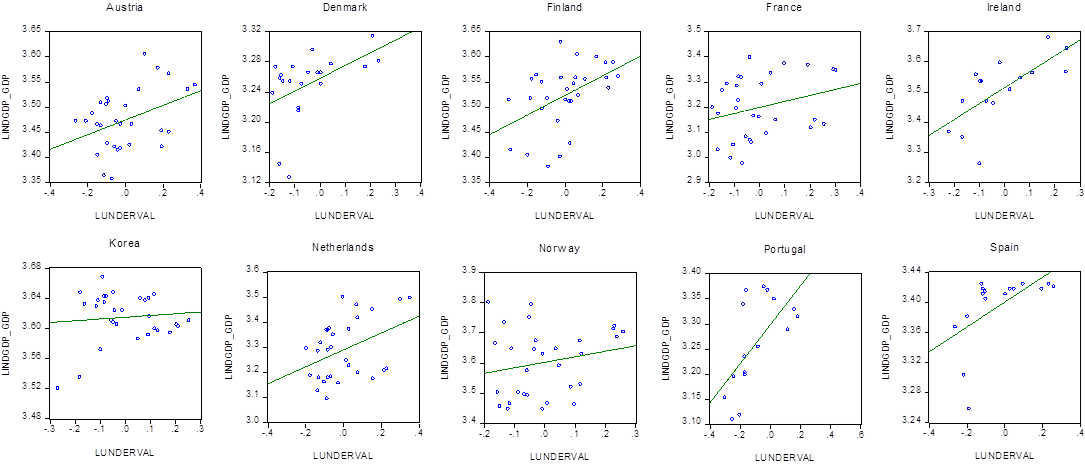
Source: Own elaboration.
Figure 2 Developed Countries, Industrial GDP/GDP and Undervaluation, 1981-2010
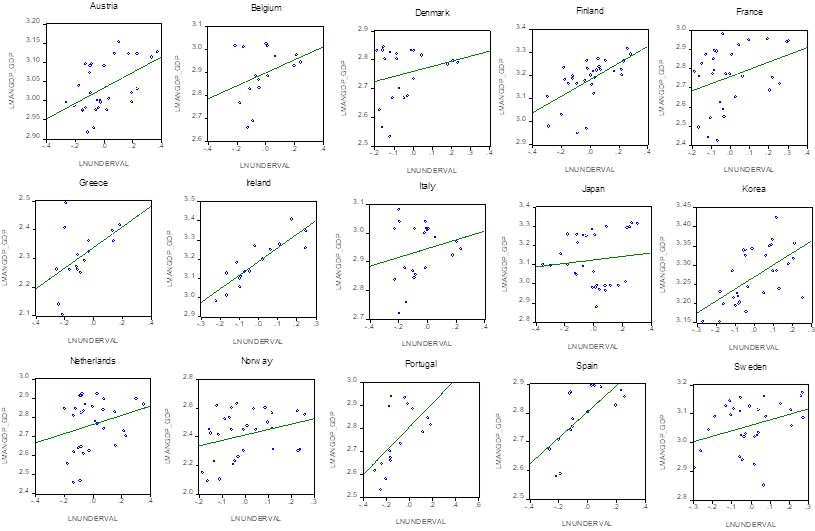
Source: Own elaboration.
Figure 3 Developed Countries, Manufacturing GDP/GDP and Undervaluation, 1981-2010
Figure 2 displays a selection of developed countries that showed a positive relationship between the ratio of Ind GDP_GDP and our undervaluation index5. Also, figure 3 displays a selection of developed countries that clearly showed a positive relationship between the ratio of Manuf GDP_GDP and our undervaluation index. Thus, it seems that, for some developed countries, one of the main channels through which economic activity has been enhanced is via the undervaluation of the currency, by which industrial and manufacturing production tend to increase in the short and long run.
Table 2 also shows that after the developed countries, the African and Asian countries have the higher long-term elasticities on the ratio Ind GDP_GDP due to an increase in undervaluation. Similarly, the LAC and Asian countries have the higher long-term elasticities on the ratio Manuf GDP_GDP due to an increase in undervaluation. These results could make more sense to the reader by looking at figures 4 and 5, which display a selection of developing countries that showed a positive relationship between the ratios Ind GDP_GDP and Manuf GDP_GDP with our undervaluation index.
Thereby, in the case of these developing countries, the results seem to suggest that the undervaluation of the currency tends to improve the level of international competitiveness and to foster higher levels of investment. By considering all these observations, it is possible to expect that an increased level of industrial and manufacturing production will trigger a higher multiplier effect on the economy in the short and long-run.
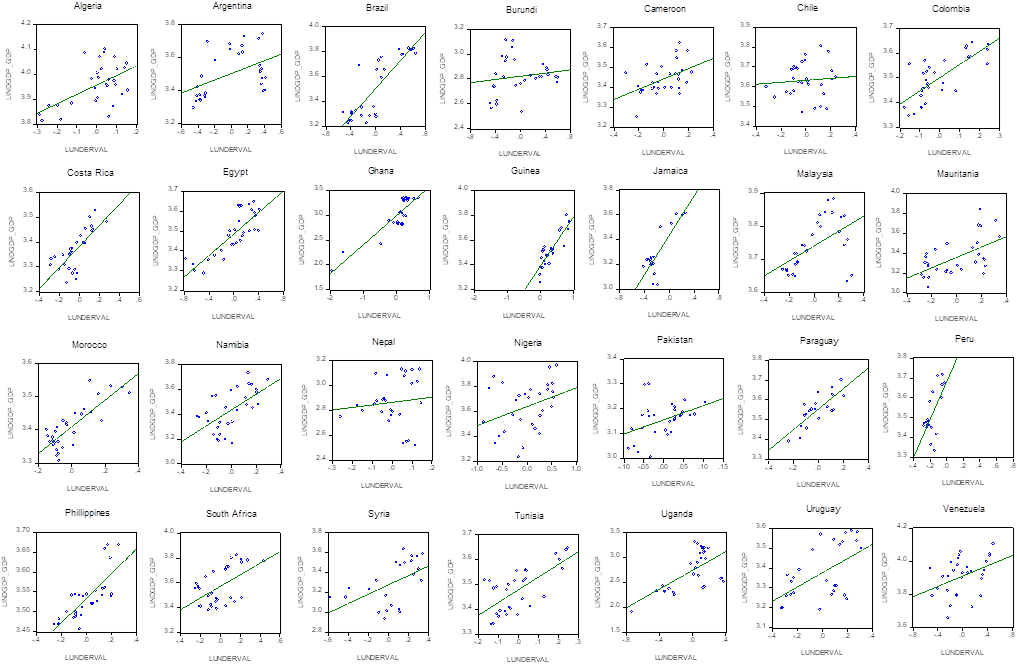
Source: Own elaboration.
Figure 4 Developing Countries, Industrial GDP/GDP and Undervaluation, 1981-2010
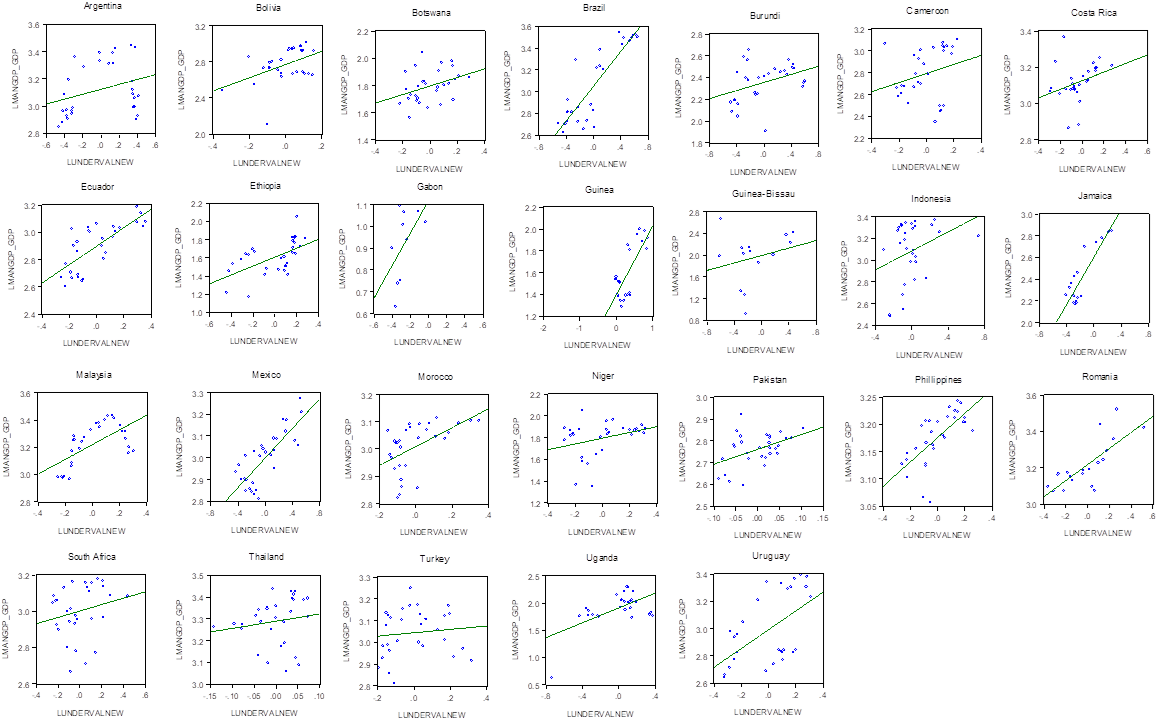
Source: Own elaboration.
Figure 5 Developing Countries, Manufacturing GDP/GDP and Undervaluation, 1981-2010
By the same token, table 3 reports the overall long-term estimates from equations 9 and 10, which relate the ratio Ind Emp_Total Emp and Inflation with the index of undervaluation. Regarding the first relation, our estimates suggest that, except for our sample of African countries, an undervalued currency has had positive effects on the ratio Ind Emp_Total Emp for all our sample of countries, having the developed and Asian countries the larger overall long-term elasticities. The developing countries turned out to have the lowest long-term elasticity. Now, figure 6 displays a selection of developed countries that showed a positive relationship between the ratio Ind Emp_Total Emp and the undervaluation index. While figure 7 displays the same relation for the case of developing countries.
Table 3 Undervaluation, industrial employment and inflation: Short and overall long-term effects, 1981-2010
| Dependent Variable | LInd. Emp./Total Emp. | LInflation | |||
| Parameter | ε* | lag(s) | Π* | lag(s) | |
| All Countries (96) | 0.35 | 0 | 1.09 | 1 | |
| Developed (25) | 0.50 | 0 | 0.84 | 0 | |
| Developing (71) | 0.12 | 0 | 1.12 | 1 | |
| Africa (35) | -0.11 | 0 | 0.64 | 0 | |
| Asia (18) | 0.23 | 1 | 0.80 | 0 | |
| L.A. (20) | 0.19 | 0 | 1.95 | 0 | |
Note: The numbers in parentheses indicate the number of countries in each panel regression. Ind. Emp/T. Emp stands for the ratio of industrial employment to total employment.
Source: Own calculations.
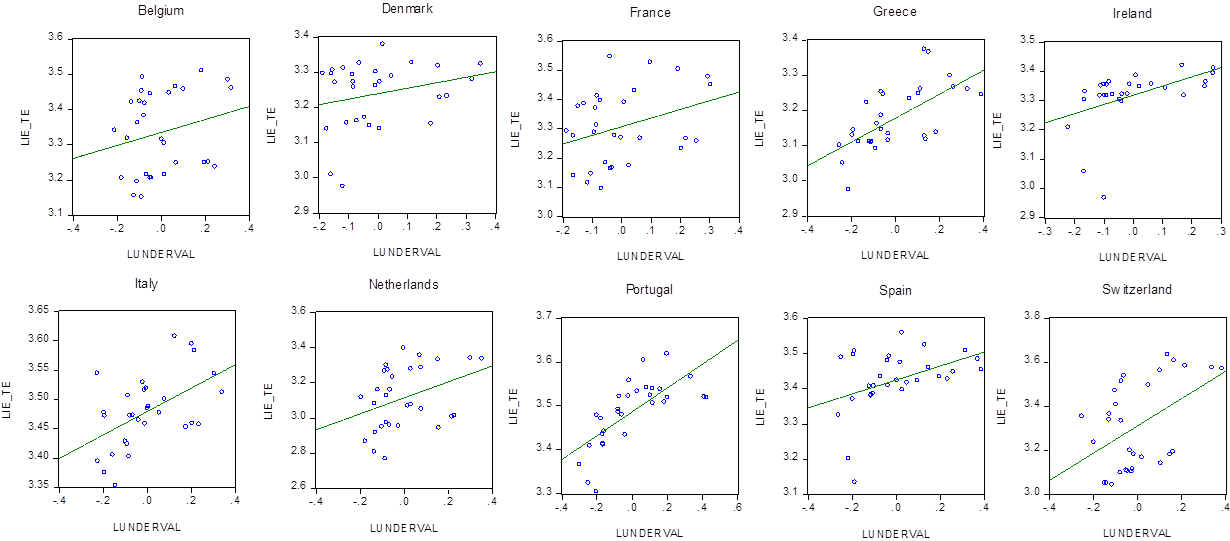
Source: Own elaboration.
Figure 6 Developed Countries, Industrial Employment/Total Employment and Undervaluation, 1981-2010
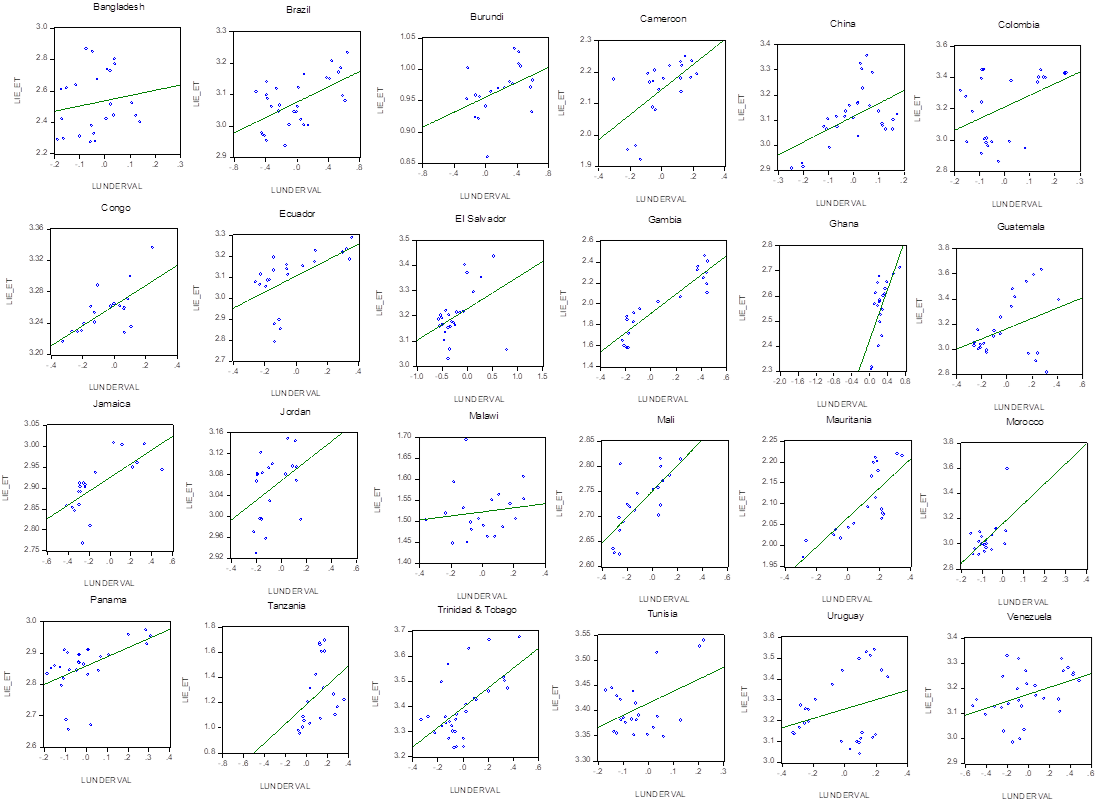
Source: Own elaboration.
Figure 7 Developing Countries, Industrial Employment/Total Employment and Undervaluation, 1981-2010
Concerning the second relation, our estimates in table 3 suggest that for all our blocks of countries, the downside effect of an undervalued currency has been an increase in the inflation rate in the short and long-term. For example, for our sample of developed, African and Asian countries, there was an incomplete pass-through effect from the changes of the undervalue index to the overall prices in the short and long-term as their elasticities turned out to be less than one.
Moreover, for the cases of our sample of developing countries as a whole and the LAC countries, our estimated results suggest that a deliberated undervalued policy would end up creating more inflation in developing countries, and especially in LAC countries, which showed a very large overall long-term effect. We believe that these results, along with redistributive issues (more on this below), indicate the main drawbacks of pursuing de facto undervalued exchange rate policies.
V. Empirical Results: Undervaluation and Aggregate Demand in the Short Run
In this section, for a selection of developed and developing countries for the period 1990-2010, our aim is to estimate the short-run multiplier effects of a change in our undervaluation index calculated in section three upon the main three sectoral balances of the economy with respect to the GDP ((I-S), (X-M), and (G-T)), the ratio of manufacturing GDP to GDP, the ratio of industrial employment to total employment, the wage-share (Wages + Salaries/GDP), and the inflation rate. With regard to the sectoral balances, it is important to highlight that a positive difference in any of these balances indicates an injection of demand, whereas a negative difference indicates a reduction (a leakage) of demand (see Shaikh, 2012). Now, in order to estimate these short-run multipliers, we made use of the ARDL methodology (see Hill et al., 2011: 378).
The main purpose of the ARDL methodology is to estimate the
In table 4 we report the period short-run interim multipliers (
In table 4, the empty cells indicate that an undervalued currency did not have any meaningful econometric short-run impact on the estimated variable; the bold squares indicate the average of each region. Considering our selection of developed countries, we can see that for some economies, an undervalued currency has some important positive effects on the excess of investment over savings and the excess of exports over imports (especially in the UK and Canada).
The inflation rate tends to be higher in three out of six countries. For the other variables, perhaps the most relevant elasticity to discuss is the ratio of
Table 4 Aggregate Demand Components: Short-Run Multipliers, 1990-2010
| Countries | (I - S) | (G - T) | (X -M) | Man.GDP/GDP | IE/TE | W/GDP | Inflation | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Belgium | 0.16 | -0.10 | 0.07 | -0.04 | ||||||||||
| Canada | 0.34 | -0.11 | 0.15 | 0.10 | ||||||||||
| France | ||||||||||||||
| Greece | -0.16 | 0.55 | 0.12 | |||||||||||
| UK | 0.54 | 0.12 | 0.49 | 0.18 | ||||||||||
| US | 0.35 | |||||||||||||
| Average by Region | 0.35 | -0.06 | 0.24 | 0.55 | 0.12 | -0.04 | 0.21 | |||||||
| Cameroon | -0.03 | |||||||||||||
| Cote d' Ivore | 0.29 | |||||||||||||
| Egypt | 0.15 | -0.16 | 0.05 | -0.32 | 0.05 | -0.12 | 0.15 | |||||||
| Nigeria | 0.39 | |||||||||||||
| South Africa | 0.17 | 0.11 | ||||||||||||
| Tanzania | -0.43 | 0.08 | -0.26 | 0.46 | ||||||||||
| Average by Region | -0.140 | 0.03 | 0.15 | -0.29 | 0.05 | -0.078 | 0.33 | |||||||
| China | 0.21 | 0.16 | 0.26 | 0.41 | 0.07 | |||||||||
| Hong Kong | -0.23 | -0.14 | 0.19 | |||||||||||
| India | ||||||||||||||
| Indonesia | 0.06 | 0.31 | -0.12 | -0.04 | 0.19 | |||||||||
| Japan | -0.05 | 0.05 | ||||||||||||
| Korea | 0.10 | -0.36 | ||||||||||||
| Malaysia | 0.73 | 1.70 | ||||||||||||
| Singapore | 0.51 | 0.46 | -0.13 | 0.13 | ||||||||||
| Thailand | ||||||||||||||
| Average by Region | 0.27 | 0.00 | 0.36 | 0.07 | 0.14 | -0.034 | 0.14 | |||||||
| Argentina | 0.08 | 0.029 | 0.12 | 0.24 | 0.03 | -0.077 | 0.089 | |||||||
| Brazil | 0.05 | 0.08 | 0.50 | -0.03 | -0.048 | 0.063 | ||||||||
| Chile | 0.04 | 0.064 | 0.16 | 0.022 | 0.078 | |||||||||
| Colombia | -0.11 | -0.11 | 0.49 | |||||||||||
| Guatemala | 1.17 | 0.376 | ||||||||||||
| Mexico | 0.12 | 0.12 | 0.84 | -0.153 | 0.469 | |||||||||
| Panama | 0.29 | -1.39 | -0.159 | 0.047 | ||||||||||
| Peru | 0.32 | 0.37 | -0.101 | |||||||||||
| Uruguay | 0.08 | 0.005 | 0.07 | 0.40 | 0.20 | -0.164 | 0.105 | |||||||
| Average by Region | 0.08 | 0.033 | 0.14 | 0.18 | 0.34 | -0.097 | 0.175 |
Source: Own calculations.
For the case of the African countries, we can observe in table 4 that in two out of six economies, a higher level of undervaluation tends, in the short run, to lead to the contraction of the economy via a reduction of the ratio
Only in the case of Egypt, an increase in undervaluation tends to worsen the distribution of income, as the wage-share would shrink by 1.2% if this economy undergoes a 10% undervaluation rate. For the cases of South Africa and Tanzania, it seems that a higher level of undervaluation tends to increase the government expenditure with respect to the GDP, stimulated perhaps by a higher tax revenue coming from a higher value of the export of commodities or from the acquisition of more public debt.
With respect to the case of the Asian countries, in four out of nine countries, the excess of investment over savings tends to improve strongly when there is an increase in undervaluation. Only in four of these economies, there is an improvement in the trade balance, especially in Malaysia, which reported a strong elasticity, 1.7%. Inflation tends to increase in four of these economies; only in the case of Japan, this increase was negligible.
The only economy that reported negative important distributive effects after a devalued currency was Singapore, where the drop in the wage-share totally matched the increase in the inflation rate. Korea showed a contractionary effect as its ratio
As for the LAC countries, this region presented mixed-effects because of an increase in undervaluation, more noticeable are the fall in the wage-share in six out of nine economies (especially in Uruguay and Mexico) and the increase in the inflation rate in seven economies (especially in Mexico and Guatemala). Regarding the positive effects due to the increase in the level of undervaluation, our results suggest that Peru had a strong increase in the level of investment over savings and in its trade balance.
Also, Panama reported a strong elasticity in its trade balance. Mexico, Brazil, and Colombia showed important positive elasticities in their ratio
In short, based on the information drawn from table 4, we could conclude that, in general, the short-run effects of real depreciation on the components of aggregate demand can be diverse, not only among different economies but also within an economy. Hence, a thorough analysis of all the economic sectors should be pursued to weigh the pros and cons of a fully-fledged competitive macro-policy through the administration of the nominal exchange rate. Finally, we want to single out the case of the LAC countries, which in general showed an important deterioration in their distribution of income (which is pretty much equivalent to a reduction on the aggregate level of consumption) when there is an increase in the undervaluation of their currencies in the short run. This pattern is not really seen in other areas of the world.
Concluding Remarks
Based on our own reformulation of Rodrik’s (2008) undervaluation index using the PWT 7.1, this investigation presents evidence of different long-run patterns in the relationship between the RER and income per capita for developed and developing countries and among developing countries. With these differences between countries in mind, we subsequently estimated the Balassa-Samuelson (B-S) effect for different sets of countries, observing different B-S effects among countries, linear and nonlinear relationships between these variables, a result that many other investigations have overlooked. Only in the study by Missio et al., (2015) using a different data set and a slightly different technique, they also found a nonlinear relationship between these variables but for a different sample of countries. The main difference is that our study found that the nonlinear relationship applies to different sets of developing countries at different times (see table 1).
Moreover, our study found, using the dynamic panel data methodology, that an undervalued currency had, for some developed and developing countries, positive long-run effects upon the trade balance, the level of investment, industrial, and manufacturing production for the period 1981-2010. In contrast, using the same undervaluation index and the ARDL methodology for the period 1990-2010, we found that an undervalued currency had expansive and contractionary effects in the short run upon aggregate demand components. Most expansionary effects took place on the trade balance and the manufacturing production ratio. Meanwhile, most negative impacts took place upon the wage-share and the inflation rate, especially in developing countries (see table 4).
Despite the foregoing empirical results, it is important to highlight the different global international trade and finance context of the twenty-first century, especially after the 2008 financial crisis, where the pace of the international demand for commodities has substantially declined, in a situation in which global supply chains have considerably reduced the national value-added of national exports (UNCTAD, 2018; UNCTAD, 2020).
In this new global context, an ongoing undervaluation of the currency would mean that the multiplier effects of exports on the entire economy would, in general, be minimal, along with a worse distribution of income; hence, nowadays, countries should not only pursue more exports with a higher national value-added component but should more importantly turn their attention to strengthen their national productive systems, especially those countries that have large internal markets.
In short, we believe that each country should make a thorough evaluation of the pros and cons of carrying out a fully-fledged undervalued exchange rate policy. Moreover, we believe that developing countries should try to undertake mixed policies to develop national industrial production and their exports through the reconnection of backward and forward linkages of their industrial systems of production.
Finally, regarding the issue of income distribution, we believe that an overvalued currency could improve the wage-share in the short-to-medium term but reduces the general level of competitiveness over time. Therefore, if a country wishes to improve its international competitiveness without significantly affecting its national distribution of income, it should make efforts to increase its international competitiveness through the development of new technologies and more differentiated products. Of course, such countries should also seek lower production costs. In the absence of a strong national bourgeoisie, the response could come from a vigorous public sector capable of developing relevant and dynamic economic sectors.











 nueva página del texto (beta)
nueva página del texto (beta)



