Clasificación JEL: C51, C52, F13, F14.
Introducción
El objetivo de este trabajo es estudiar la evolución de los flujos de comercio exterior de México de 1980 a 2000, periodo que incluye importantes cambios institucionales, como la adhesión de México al GATT (1985) y el inicio del Tratado de Libre Comercio de América del Norte (TLCAN) en 1994. El notorio desempeño del comercio exterior mexicano en los años recientes1 ha sido un tema frecuente tanto en análisis de política económica como en la prensa. Sin embargo, la mayoría de los estudios rigurosos de este tema se han centrado en evaluar únicamente los cambios ocurridos en los años noventa.
Gould (1998) encontró que el comercio de Canadá con los Estados Unidos y México no tuvo efectos perceptibles después del TLCAN, pero que el comercio entre México y los Estados Unidos sí mostró cambios notorios. Este autor basó sus cálculos en un modelo de gravedad del comercio bilateral, en el que el cambio en las barreras tarifarias y no tarifarias es aproximado con una variable dicotómica que resultó significativa para las ecuaciones de comercio entre México y los Estados Unidos.
Por su parte, Krueger (1999) señala que tanto el comercio canadiense como el mexicano se han tornado más concentrados hacia los Estados Unidos e indaga, también en el contexto de un modelo de gravedad, si dicho fenómeno es resultado de la creación o de la desviación de comercio. La autora concluye que el TLCAN no indujo grandes efectos respecto a otros procesos ya en marcha, como la reducción previa de tarifas y la modificación del régimen del tipo de cambio en México. Gruben (2001) encuentra que el TLCAN ha tenido poca influencia en el empleo en las plantas maquiladoras mexicanas.
El interés en el estudio de los efectos del TLCAN en el comercio exterior mexicano es comprensible por ser este acuerdo uno de los sucesos económicos e institucionales más importantes del decenio pasado. Un factor adicional que quizá explique el hincapié en la experiencia reciente es la dificultad de obtener modelos econométricos que abarquen periodos largos, debido a posibles cambios estructurales en las relaciones económicas o modificaciones metodológicas en la elaboración de las estadísticas. Por ejemplo, en un elaborado estudio para muchos países con datos anuales de 1960 a 1993, Senhadji y Montenegro (1998) no lograron obtener cifras con el signo correcto para la función de exportaciones de México. Esto probablemente obedeció a alguna de las causas mencionadas, ya que su metodología parece apropiada y fue exitosa en muchos otros de los casos que ellos analizan.2 En este trabajo se examina de manera más pormenorizada la evolución de los flujos comerciales de México y analiza el comportamiento de las funciones de demanda y no se hace ningún intento de estimar funciones de oferta.
Debido a la menciona da dificultad de obtener modelos para todo el periodo 1980-2000, éste se divide en dos submuestras, 1980-1989 y 1990-2000, en que se destaca la incorporación de México al GATT y al TLCAN, respectivamente. Aunque se da una relevancia mayor al estudio de la segunda submuestra, también se obtienen modelos de largo plazo para la primera. El análisis se realiza con el uso simultáneo de varios métodos de estimación de relaciones de largo plazo.
Los resultados principales se señalan a continuación. Se obtienen coeficientes con el signo correcto y magnitud razonable en la estimación de funciones de demanda de largo plazo para las exportaciones e importaciones en el periodo 1990-2000. La ecuación de exportaciones es función del índice de la producción de los Estados Unidos y del tipo de cambio real y resulta muy estable para dicho periodo. La función de importaciones, que depende del índice de la producción industrial de México, del monto de las exportaciones y del tipo de cambio real, muestra inestabilidad, aunque la ecuación ajusta los datos muy bien aun sin considerar la estacionalidad o la dinámica de corto plazo.
El análisis se extiende para datos desagregados del periodo 1980-2000 y se obtiene que solamente en unos pocos casos se puede encontrar cointegración para toda la muestra (1980-2000) y en ningún caso el vector correspondiente es estable. Para el periodo 1990-2000 se obtuvo un vector de cointegración estable en todos los casos. La inestabilidad de la ecuación de las importaciones totales para la submuestra 1990-2000 no se transfiere a los datos desagregados. También se obtienen modelos de corrección de error estables y constantes para igual periodo.
En la mayoría de los casos, pudieron obtenerse vectores de cointegración para la submuestra 1980-1989, aunque éstos no pasan las pruebas de estabilidad. Los resultados anteriores indican que si bien un cambio estructural en el comercio exterior de México durante los años noventa no parece haber se realizado, uno muy importante fue inducido por la apertura de la economía y la incorporación de México al GATT en los años ochenta. Por esa razón no es posible, en general, encontrar relaciones estables comenzando desde 1980.
El resto del documento está organizado como sigue: en la sección I se describe los datos y se explora la presencia de raíces unitarias en ellos. En la sección II se analiza el comportamiento de las exportaciones e importaciones a nivel más agregado. En la sección III se estudia diferentes tipos de exportaciones e importaciones. En la sección IV se analiza los modelos de corrección de error. Al final se proporciona las conclusiones.
I. Descripción y propiedades estadísticas de los datos
Los datos de exportaciones e importaciones totales (X y M, respectivamente) se expresan en dólares constantes y tienen una periodicidad mensual.3 Las exportaciones están desagregadas en maquila (X {Q} ), derivados del petróleo (X {O} ) y el resto (X {−QO} ). Las importaciones están subdivididas en bienes de consumo (M {cons} ), bienes de capital (M {cap} ) y bienes intermedios (M {int} ). También se consideran las importaciones de bienes intermedios para maquila (M {intQ} ) y el resto (M {int−Q} ). El tipo de cambio real bilateral peso/dólar (TCR) está basado en los respectivos índices de precios al consumidor.
Las variables de escala son el índice de valor de la producción industrial de los Estados Unidos (ivusa) y el índice de valor de la producción industrial de México (ivpi). Los nombres de las variables en letras pequeñas indican el uso de logaritmos.
En el cuadro 1 se presentan dos pruebas (con tres y seis rezagos) para clasificar los logaritmos de las series como de tendencia estacionaria (TS) o diferencia estacionaria (DS). La primera es la prueba DFGLS propuesta por Elliot et al (1996), la cual es una versión más poderosa de la bien conocida prueba ADF. La segunda es la prueba KPSS de estacionariedad propuesta por Kwiatkowski et al (1992). Estas pruebas, u otras similares, se usan conjuntamente en análisis confirmatorios de la presencia de una raíz unitaria en las series.4
Cuadro 1 Pruebas de raíces unitarias
| Variable | DFGLS | PSS2 | ||||
| 3 rezagos | 6 rezagos | 3 rezagos | 6 rezagos | |||
| Niveles | ||||||
| x | −1.8 | −0.9 | 1.3** | 0.8** | ||
| x {−QP} | −1.7 | −1.3 | 0.5** | 0.3** | ||
| x {Q} | −2.9** | −2.2 | 0.2** | 0.2** | ||
| m | −1.5 | −1.8 | 0.7** | 0.4** | ||
| m {cap} | −1.5 | −1.5 | 0.7** | 0.4** | ||
| m {cons} | −1.8 | −2.0 | 0.6** | 0.3** | ||
| m {int} | −1.7 | −1.6 | 0.7** | 0.4** | ||
| m {intQ} | −3.2** | −2.5 | 0.2** | 0.1 | ||
| m {int−Q} | −1.7 | −1.7 | 0.7** | 0.4** | ||
| ivusa | −1.1 | −1.4 | 0.7** | 0.4** | ||
| ivpi | −1.8 | −1.7 | 0.8** | 0.5** | ||
| tcr | −1.6 | −1.9 | 0.5** | 0.3** | ||
| Diferencias | ||||||
| x | −8.9** | −3.7*** | 0.0 | 0.0 | ||
| x {−QP} | −8.1*** | −3.7** | 0.0 | 0.0 | ||
| x {Q} | −10.6*** | −6.2*** | 0.0 | 0.0 | ||
| m | −7.8*** | −5.4*** | 0.1 | 0.1 | ||
| m {cap} | −5.2*** | −2.8* | 0.0 | 0.1 | ||
| m {cons} | −6.8 | −4.2*** | 0.1 | 0.1 | ||
| m {int} | −6.0*** | −3.7*** | 0.0 | 0.0 | ||
| m {intQ} | −10.1*** | −6.1*** | 0.0 | 0.0 | ||
| m {int−Q} | −5.7*** | −3.8*** | 0.0 | 0.0 | ||
| ivusa | −6.7*** | −5.1*** | 0.1 | 0.1 | ||
| ivpi | −9.5*** | −5.6*** | 0.0 | 0.0 | ||
| tcr | −8.3*** | −5.5*** | 0.1 | 0.1 | ||
* 10% de significación.
** 5% de significación.
*** 1% de significación.
En todos los casos excepto dos (con tres rezagos) la prueba DFGLS no rechaza la presencia de una raíz unitaria en los niveles de las series. El resultado es confirmado por el rechazo del estadístico KPSS a la hipótesis de estacionariedad en todos excepto uno de los casos (con seis rezagos). Para las diferencias de las series (tasas de crecimiento) los resultados son los opuestos: el estadístico DFGLS rechaza la hipótesis de una raíz unitaria en todos los casos y el KPSS no puede rechazar la hipótesis de estacionariedad. Por ello, se procede al análisis considerando que todas las series son I(1). Los resultados de este documento se mantienen inalterados aún si el tipo de cambio real se considera una variable I(0).
II. Análisis del comercio exterior agregado de México
En la gráfica 1 se muestra en sus dos partes con una línea continua a la balanza comercial de México, medida como x-m en lugar de X-M. La línea punteada en la par te superior representa la diferencia del logaritmo de los índices de la producción industrial de México (ivpi) y de los Estados Unidos (ivusa), como un indicador del ingreso relativo. La línea punteada en la parte inferior representa la trayectoria del logaritmo del tipo de cambio real (tcr).
La gráfica sugiere que la balanza comercial mexicana empeora cuando la actividad de México crece más rápido que la de Estados Unidos y lo mismo ocurre cuando el tipo de cambio real se aprecia. El análisis econométrico se basa en considerar un vector y t = (y 1t , y 2t ) de k variables económicas no estacionarias que forman un sistema cointegrador que puede ser interpretado como una demanda de largo plazo y 1 de importaciones o exportaciones, dependiendo de otras k − 1 variables y 2 en una forma lineal:
en que
1. Exportaciones
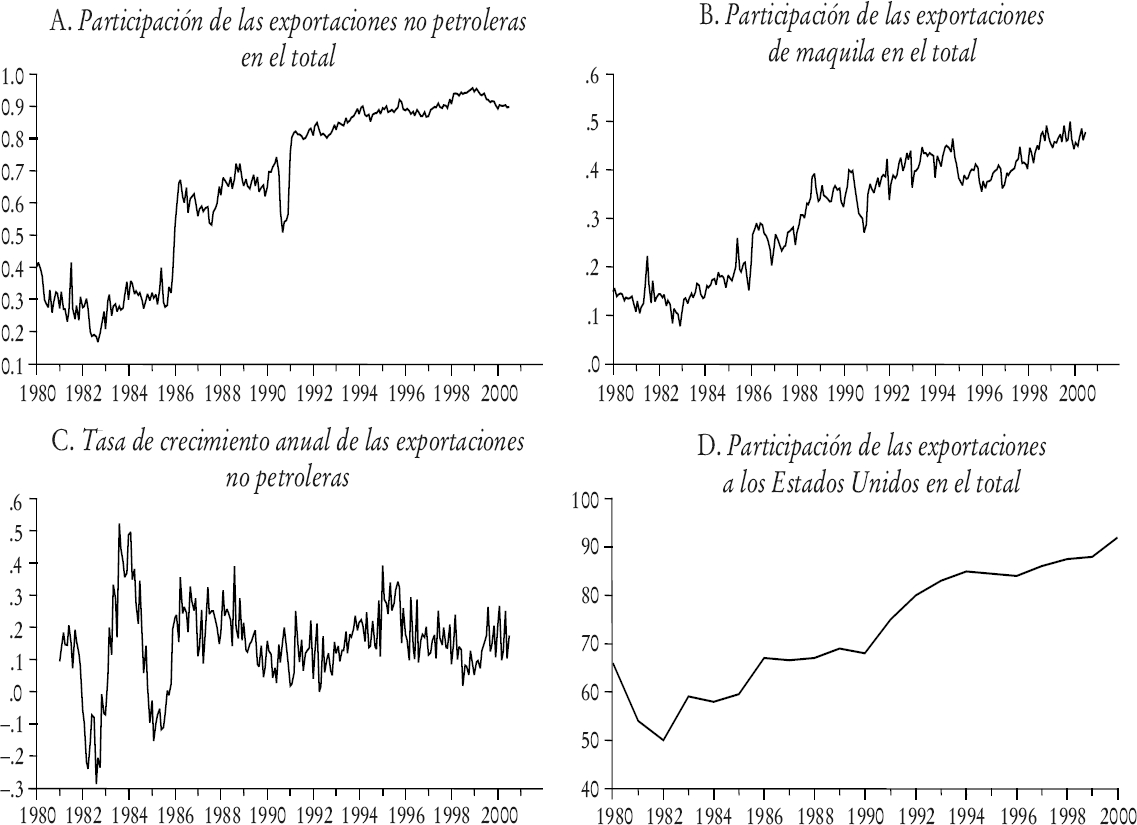
En las cuatro partes de la gráfica 2 se observa que desde 1980 ha habido cambios muy importantes en la composición, la tasa de crecimiento y el destino de las exportaciones mexicanas. En la par te A se aprecia que la participación de las exportaciones no petroleras en el total ha aumentado cerca de 50% al inicio de los años ochenta hasta alrededor de 90% en 2000. En la parte B se muestra un comportamiento similar de las exportaciones de maquila, las cuales han incrementado su participación en el total hasta alrededor de 50%, partiendo de 15% en los inicios de los años ochenta.
En la parte C se ilustra cómo la evolución de las exportaciones ha cambiado desde la segunda mitad de los años ochenta, una vez que México se unió al GATT. Las abruptas variaciones al comienzo de la muestra obedecen a la crisis económica que inició en 1982 y a la aplicación de medidas restrictivas al comercio internacional y son una probable causa de la dificultad para estimar una función de exportaciones para todo el periodo considerado. En la última parte, que utiliza observaciones anuales por falta de datos mensuales antes de los años noventa, se señala que la tendencia de las exportaciones mexicanas a concentrarse en los Estados Unidos comenzó desde los ochenta.6 En esta sección se modela la demanda de exportaciones mexicanas totales (x) como una función lineal del índice de la producción industrial de los Estados Unidos (ivusa) y del tipo de cambio real (tcr) únicamente para la submuestra de 1990 a 2000 (los diez años previos se estudian líneas abajo). Se aplica el procedimiento de Johansen (1988) para estudiar el sistema formado por estas tres variables. Los resultados se presentan en el cuadro 2.
Cuadro 2 Análisis de máxima verosimilitud para exportaciones (1990-2000)a
| i) | Análisis de cointegración | ||||
| Eigenvalores | 0.215 | 0.054 | 0.027 | ||
| Hipótesis nula | ran = 0 | ran < 2 | ran < 3 | ||
| λ traza | 42.280** | 10.520 | 3.459 | ||
| Val. crit. (95%) | 29.700 | 15.400 | 3.800 | ||
| ii) | Estandarización del vector de cointegración y ajuste de los coeficientes | ||||
| Variable | x | IPI {USA} | tcr | ||
| Ver. coin. nort. γ | 1.000 | −2.800 | −0.318 | ||
| Ajuste de coef. α | −0.400 | 0.017 | 0.043 | ||
| iii) | Prueba de significación, exogeneidad débil y exogeneidad fuerte de una variable dada | ||||
| Variable | x | IPI {USA} | tcr | ||
| Exclusión X 2(1) | 21.247** | 19.382** | 10.656** | ||
| Exog. débil X 2(1) | 16.100** | 5.168* | 0.455 | ||
| iv) | Pruebas de especificación | ||||
| Ecuación | x | IPI {USA} | tcr | Prueba conjunta | |
| ARF (7,102) | 4.40[.00] | 0.75[.37] | 1.11[.37] | F(63 257 = 2.01[.00]** | |
| Normalidad X 2 (2) | 0.99[.61] | 5.36[.07] | 73.98[.00]** | X 2 (6) = 76.44[.00]** | |
| Heterosc. F(12.96) | 1.35[.20] | 1.59[.11] | 3.08[.00]** | F(72 500) = 1.47[.01]* | |
a Los valores de probabilidad están entre paréntesis. Una descripción pormenorizada de las pruebas aquí proporcionadas se pueden obtener en Hendry (1995).
* 10% de significación.
** 5% de significación.
*** 1% de significación.
La sección i) del cuadro 2 contiene los estadísticos de la traza para las hipótesis secuenciales de 0 vectores, al menos un vector y a lo más dos vectores de cointegración. Únicamente la primera hipótesis se rechaza y se concluye que hay solamente una relación de largo plazo entre las variables implicadas. Este hecho permite que al darse un coeficiente unitario a las exportaciones (x), los otros coeficientes de la relación sean interpretables como elasticidades de largo plazo.
En la sección ii) se presentan los coeficientes de cointegración ya normalizados. Estos tienen el signo correcto y resultan ser muy similares a los que se obtienen líneas abajo con un método diferente. Los estimados implican la siguiente demanda de largo plazo de las exportaciones totales en dólares constantes (x):
En la sección iii) del cuadro se incluyen las pruebas de exclusión y exogeneidad débil. Éstas demuestran que ninguna de las tres variables puede ser eliminada de la relación de largo plazo y que sólo para las exportaciones totales se rechaza la hipótesis de exogeneidad débil. Lo anterior justifica el análisis más pormenorizado que se realiza líneas abajo utilizando métodos uniecuacionales, aunque una observación es importante en vista de que las pruebas de especificación no fueron completamente satisfactorias. Aunque se intentó corregir la no normalidad de los residuales del VAR con variables dicotómicas, es te proceso requería demasiadas de ellas para el tamaño de la muestra. Esto es desafortunado dado que la propiedad de normalidad es un requisito para que las pruebas de esta sección sean estrictamente válidas. Dada esta circunstancia, también presente en la ecuación de las importaciones, se optó por un método de análisis algo diferente para los datos desagregados el cual es más sólido en presencia de no normalidad.
Finalmente, se aplicó una prueba sencilla para evaluar la estabilidad de la
función de las exportaciones mexicanas durante el periodo 1990-2000. Este
procedimiento consiste en estimar recursivamente el sistema y probar con un
cociente de verosimilitud (distribuido como una
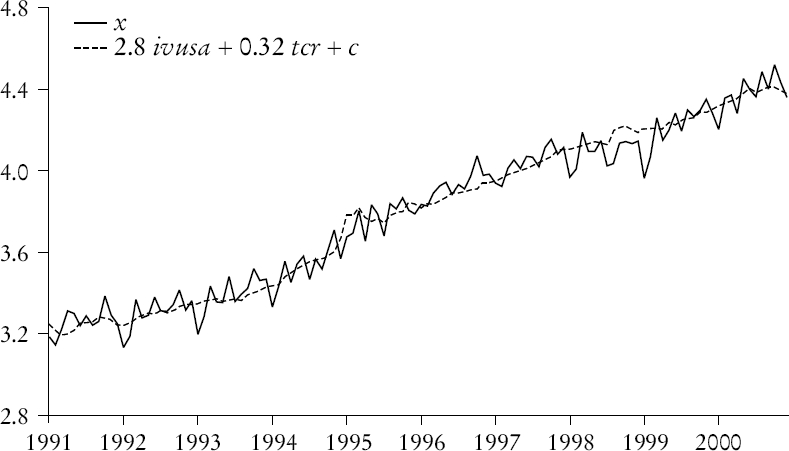
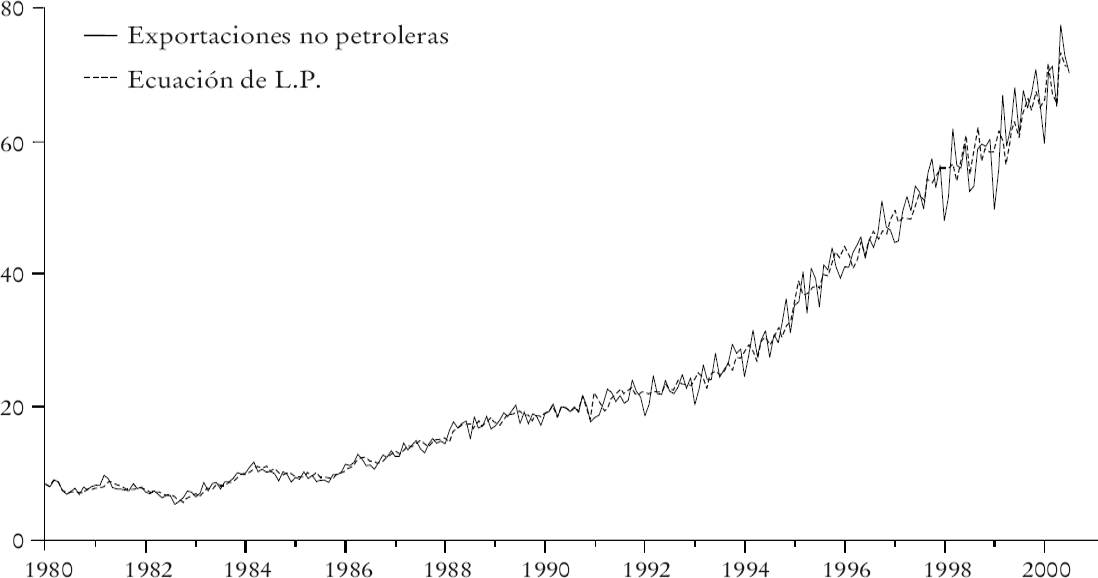
La hipótesis de parámetros constantes es claramente confirmada por los datos. Sobre la base de este resultado y con la salvedad mencionada, puede afirmarse que en la muestra no hay información suficiente para señalar un cambio estructural en la conducta de las exportaciones mexicanas durante los años noventa. Sin embargo, este resultado puede ser el producto del nivel de agregación usado en el análisis. Por ello, un análisis con datos más desagregados es necesario. Ejemplo de ello es la trayectoria de las exportaciones petroleras, la cual probablemente no responde a factores de mercado de la misma manera en la que la de otro tipo de exportaciones lo hace.7 La precisión del ajuste del modelo se muestra en la gráfica 4.
La bondad del ajuste gráfico es muy aceptable a pesar de no incluir la dinámica de corto plazo ni los efectos estacionales. En el periodo 1994-2000, el crecimiento del nivel de equilibrio de las exportaciones mexicanas se debe principalmente a la mayor fortaleza de la economía de los Estados Unidos. De 1990 a 1993 las exportaciones aumentaron menos porque la economía de ese país lo hacía a un paso mucho más lento y el tipo de cambio estaba bastante más apreciado.8
2. Importaciones
Durante los años ochenta las importaciones fueron a menudo objeto de una política comercial restrictiva y fueron influidas por una serie de grandes devaluaciones. Después de que México entrara al GATT, a la mitad de los ochenta, la mayor parte de las restricciones no tarifarias fueron removidas, los gravámenes fueron reducidos y la volatilidad del tipo de cambio se atenuó considerablemente. En las cuatro partes de la gráfica 5 se muestran algunos aspectos de la trayectoria de las importaciones.
En la parte A se observa la tasa de crecimiento anual de las importaciones totales. Las devaluaciones históricamente han tenido un gran efecto en dicha variable y algunas veces arribaron junto con severas contracciones de la actividad interna y en el contexto de una política comercial restrictiva (esto último al principio de los años ochenta). La gran caída que se observa en 1983 ocurrió a consecuencia del estallido de la crisis de la deuda.
En la parte B se presenta la participación de las importaciones de consumo en el total. Este tipo de importaciones tiene el efecto ingreso más alto. La expansión económica y el aumento del consumo al principio de los años noventa coincidió con la etapa en la que las importaciones de este tipo de bienes tuvieron su mayor participación en el total.
En la parte C se incluye la participación de las importaciones de bienes intermedios en el total. Este es el componente más importante de las importaciones mexicanas y ha estado creciendo desde el comienzo de la muestra, representando actualmente cerca de 80% del total. En la última parte se muestra la participación de los bienes intermedios importados por las maquilas. Este es, por mucho, el componente más vigoroso de las importaciones mexicanas y actualmente se acerca a 30% del total.
Se aplicó el procedimiento de Johansen a un sistema de variables que incluye importaciones mexicanas totales (m), el índice mexicano de la producción industrial (ivpi), el tipo de cambio real (tcr) y el nivel de las exportaciones totales (x). La muestra considerada en esta sección se extiende de 1991 a 2000. Los resultados se presentan en el cuadro 3.
Cuadro 3 Análisis de máxima verosimilitud para las importaciones (1990-2000)a
| i) | Análisis de cointegración | |||||
| Eigenvalores | 0.222 | 0.136 | 0.029 | 0.002 | ||
| Hipótesis nula | ran = 0 | ran < 1 | ran < 2 | ran < 3 | ||
| λ traza | 48.59** | 20.170 | 3.599 | 0.251 | ||
| Val. crit. (95%) | 47.200 | 29.700 | 15.400 | 3.800 | ||
| ii) | Estandarización del vector de cointegración y ajuste de los coeficientes | |||||
| Variable | m | ivpi | tcr | x | ||
| Ver. coin. nort. γ | 1.000 | −0.937 | 0.410 | −0.530 | ||
| Ajuste de coef. α | −0.712 | −0.178 | 0.113 | −0.365 | ||
| iii) | Prueba de significación, exogeneidad débil y exogeneidad fuerte de una variable dada | |||||
| Variable | m | ipvi | tcr | x | ||
| Exclusión X 2(1) | 27.98** | 24.99** | 17.29** | 26.23** | ||
| Exog. débil X 2(1) | 16.63** | 4.84 | 1.23 | 4.14 | ||
| iv) | Pruebas de especificación | |||||
| Ecuación | m | ipvi | tcr | x | Prueba conjunta | |
| ARF (7,102) | 2.43[.03]* | 2.29[.03]* | 2.00[.06] | 4.97[.00] | F(112,292 = 1.83[.00]** | |
| Normalidad X 2 (2) | 0.12[.51] | 1.35[.51] | 62.46[.00]** | 0.61[.74] | X 2 (8) = 64.74[.00]** | |
| Heterosc. F(12.96) | 1.10[.37] | 1.58[.09]* | 3.36[.00]** | 1.84[.04] | F(160,685) = 1.59[.00] | |
a Los valores de probabilidad están entre paréntesis. Una descripción pormenorizada de las pruebas aquí proporcionadas se pueden obtener en Hendry (1995).
* 10% de significación.
** 5% de significación.
Estos resultados son muy similares a los que se obtuvieron en el caso de las exportaciones: hay un solo vector de cointegración, las elasticidades de largo plazo tienen el signo correcto, ninguna de las variables puede ser excluida y solamente para la variable importaciones se rechaza la hipótesis de exogeneidad débil. La demanda de largo plazo para las importaciones es la siguiente:
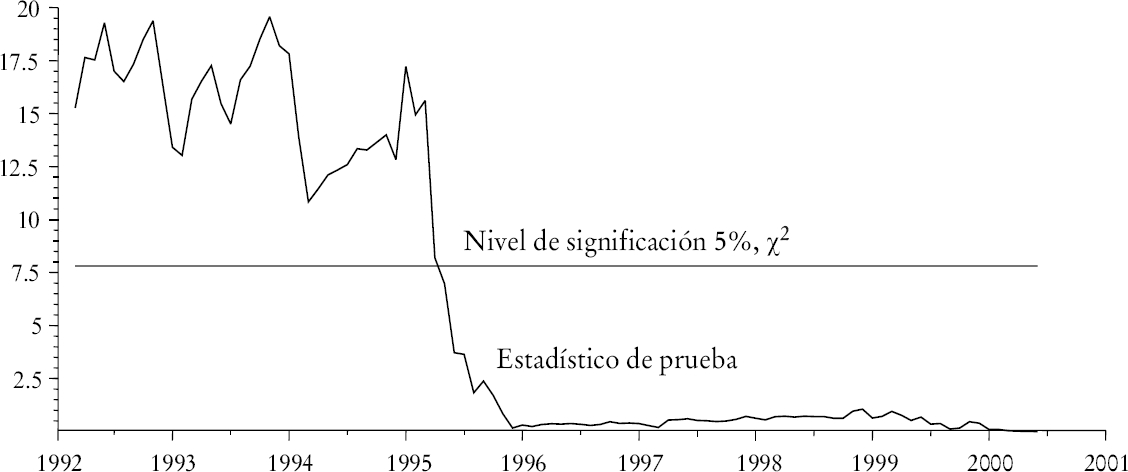
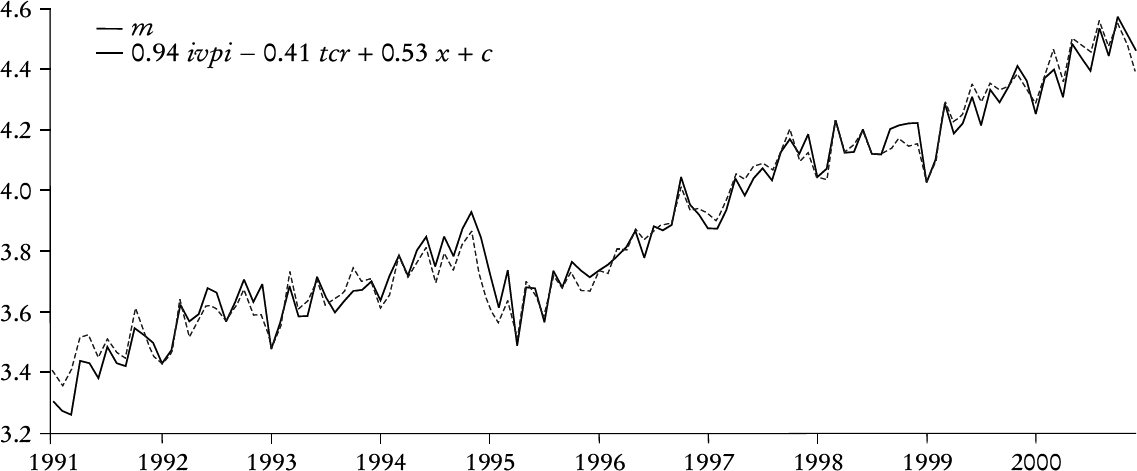
El resultado de las pruebas de estabilidad, sin embargo, es diferente. Como se indica en la gráfica 6 la secuencia de estadísticos del cociente de verosimilitud cruza la línea de significación. Esto podría ser interpretado como indicativo de que un cambio estructural en las importaciones mexicanas ocurrió durante los años noventa. Sin embargo, un análisis más pormenorizado sería necesario. Por ejemplo, el modelo de corrección que se presenta más adelante exhibe estabilidad. Otro argumento contra la hipótesis de cambio estructural en los noventa lo ofrece el hecho de que la ecuación de largo plazo ajusta los datos extremadamente bien, tal como se muestra en la gráfica 7.
III. Análisis de los datos desagregados
Aunque algunos posibles cambios en las relaciones económicas fueron tomados en consideración al dividirse la muestra, los resultados obtenidos de las exportaciones e importaciones totales podrían no confirmarse a un nivel desagregado. Para considerar esta posibilidad, además de incluir todos los años disponibles en la muestra, se estimó y se examinó la estabilidad de las funciones de exportaciones e importaciones desagregadas para el periodo completo 1980-2000 y los subperiodos 1980-1989 y 1990-2000. Debido al alto número de funciones estimadas se utilizó el marco del modelo de corrección no restringido, que generalmente produce los mismos resultados que el enfoque de máxima verosimilitud presentado en la sección anterior, pero es más sencillo.
Primero se somete a prueba la propiedad de cointegración para las diferentes definiciones y submuestras y luego se determina la estabilidad de las funciones que tienen tal propiedad. Esto último se realiza con las pruebas de estabilidad de Hansen (1992) para regresiones con variables I(1) con el método de FM-LS. Los estimados para los datos agregados resultaron muy similares con cada método utilizado y este último es más sólido en cuanto a los problemas de no normalidad comentados líneas arriba.
1. Existencia de relaciones de largo plazo con datos desagregados
Se dividió a las exportaciones en maquila (x {Q} ), petroleras (x {O} ) y el resto c(x {−QO} ). Las importaciones se desagregaron en bienes de consumo (m {c} ), bienes de capital (m {k} )y bienes intermedios (m {i} ). También se consideraron las importaciones de bienes intermedios para maquila (m {iq} ) y el res to (m {i−q} ). Para cada categoría se estimaron modelos de corrección de error no restringidos para cada submuestra.
En el cuadro 4 se registran solamente los casos en que había evidencia de cointegración para los diferentes tipos de exportaciones. Debido a que los estimados de los vectores de cointegración son muy similares con cada uno de los métodos aplicados, no se presentan las ecuaciones correspondientes. En la columna 3 se proporciona el número de variables en la relación de cointegración k. La columna 4 contiene el número de componentes determinísticos d. La columna 5 indica el tamaño de la muestra T y la columna 6 el número total de regresores h. La columna 7 corresponde el estadístico ECM.9 La columna final proporciona el valor p para cada estadístico generado por el programa de Ericsson y McKinnon (1999). Cada caso es interesante en sí mismo.
Cuadro 4 Pruebas del ECM para las exportaciones
| Variable | Periodo |
Número de variables
en el vector de cointegración k |
Número de
variables determinísticas d |
Tamaño de
la muestra T |
Número total
de regresores h |
Estadístico ECM t |
Valor pa p |
| x | 1990-2000 | 3 | 1 | 127 | 7 | −6.38 | 0.00 |
| x {−QP} | 1980-2000 | 3 | 1 | 234 | 7 | −3.67 | 0.04 |
| 1980-1989 | 3 | 1 | 107 | 7 | −3.38 | 0.07 | |
| 1991-2000 | 3 | 1 | 114 | 7 | −4.80 | 0.00 | |
| x {Q} | 1980-2000 | 2 | 1 | 234 | 6 | −2.72 | 0.15 |
| 1980-1989 | 2 | 1 | 107 | 6 | −3.90 | 0.01 | |
| 1991-2000 | 2 | 1 | 113 | 6 | −4.88 | 0.00 |
a Los valores críticos y los valores p fueron obtenidos usando el método de Ericsson y Mackinnon (1999), como instrumento en el programa ECMtest.xls (versión 1.0).
Para las importaciones totales (x) solamente se encontró cointegración para el periodo 1990-2000 (valor p = 0.0) y no para la muestra completa y la razón se puede inferir del análisis de los datos desagregados. El caso de las exportaciones de maquila (x {Q} ) puede explicar la situación. Primero que todo, la relación de cointegración excluye al tipo de cambio real (por ello k = 2). Segundo, para toda la muestra el estadístico ECM no es significativo (−2.72 con valor p = 0.15). Sin embargo, para cada submuestra, el estadístico ECM lo es. Este es un caso probable de cambio estructural (como se verá, el vector de cointegración es muy diferente para cada submuestra) del tipo sugerido por Gregory y Hansen (1996), en el que un cambio estructural esconde la existencia de una relación de largo plazo entre las variables I(1).10 Estas características de las exportaciones de maquila explican el problema de encontrar cointegración para las exportaciones totales. El caso de las exportaciones no petroleras y de no maquila (x {−QO} ) muestra cointegración para los tres periodos y las variables cointegrantes son las mismas que las relativas a las exportaciones totales.
En el cuadro 5 se muestra que en importaciones totales hay cointegración solamente para el periodo 1990-2000. Para esta categoría las variables cointegrantes son el índice de la producción industrial, el tipo de cambio real y las exportaciones (k = 4). Las mismas variables cointegrantes aparecen en el caso de las importaciones de bienes intermedios, pero las exportaciones no están en las ecuaciones de importaciones de bienes de capital y bienes de consumo (k = 3).
Cuadro 5 Pruebas del ECM para las exportaciones
| Variable | Periodo |
Número de variables
en el vector de cointegración k |
Número de
variables determinísticas d |
Tamaño de
la muestra T |
Número total
de regresores h |
Estadístico ECM t |
Valor pa p |
| m | 1991-2000 | 4 | 1 | 113 | 8 | −5.46 | 0.00 |
| m {cap} | 1980-2000 | 3 | 1 | 243 | 6 | −6.00 | 0.00 |
| 1980-1989 | 2 | 1 | 116 | 6 | −4.02 | 0.01 | |
| 1991-2000 | 3 | 1 | 114 | 6 | −6.85 | 0.00 | |
| m {cons} | 1980-2000 | 3 | 1 | 234 | 8 | −3.93 | 0.02 |
| 1980-1989 | 3 | 1 | 107 | 8 | −3.71 | 0.03 | |
| 1991-2000 | 3 | 1 | 114 | 8 | −5.20 | 0.00 | |
| m {int} | 1991-2000 | 3 | 1 | 113 | 6 | −6.37 | 0.00 |
| m {intQ} | 1991-2000 | 3 | 1 | 113 | 9 | −4.81 | 0.00 |
| m {int−Q} | 1980-2000 | 3 | 1 | 245 | 7 | −3.38 | 0.07 |
| 1991-2000 | 3 | 1 | 113 | 7 | −6.82 | 0.00 |
a Los valores críticos y los valores p fueron obtenidos usando el método de Ericsson y Mackinnon (1999), como instrumento en el programa ECMtest.xls (versión 1.0).
El caso de las importaciones de bienes de capital (m {cap} ) es notorio porque la presencia de cointegración para toda la muestra esconde la existencia de un cambio estructural de un tipo especial. Se encuentra cointegración en los tres periodos, pero los vectores de las dos submuestras contienen un número diferente de componentes: k = 3 para el periodo 1990-2000 y k = 2 para el periodo 1980-1989. En lo anterior, la variable que sale de la relación de cointegración es el índice de la producción industrial de México. Esta situación de cambio estructural, sin embargo, fue detectada por las pruebas de estabilidad que se presentan líneas abajo. Para las importaciones de consumo (m {cons} ) se encontró cointegración para los tres periodos y el mismo número de variables aparece en cada caso. Sin embargo, como se verá, también hay evidencia de un cambio estructural.
Para bienes intermedios (m {int} ) sólo se encontró cointegración para el periodo 1991-2000. Como este es por mucho el componente más grande de las importaciones mexicanas, la falta de cointegración se pasa al total. Al dividir esta categoría entre los bienes que van a maquilas (m {intQ} ) y el resto (m {int-Q} ) se llega a resultados similares.
2. Estabilidad de las relaciones de largo plazo con datos desagregados
En esta subsección se examina la estabilidad de las relaciones de largo plazo encontradas antes. Para los mismos casos presentados en el cuadro 4, se estimaron coeficientes de cointegración con el método de cuadrados mínimos completamente modificados (FM-LS por sus siglas en inglés) y se aplicaron tres pruebas de estabilidad para variables I(1) propuestas por Hansen (1991). Las tres tienen como hipótesis nula coeficientes de cointegración constantes durante toda la muestra. Las primeras dos (LC y F prom) tienen a una caminata aleatoria como opción mientras que la tercera (F sup) tiene a un cambio de una sola vez en una fecha desconocida.11
Las columnas 3-5 del cuadro 6 contienen los estimados FM-LS de los coeficientes de largo plazo de las funciones de exportaciones junto con los errores estándar para cada una de las variables cointegrantes y una constante. En las columnas 6-8 se presenta el valor de los estadísticos para probar estabilidad y los respectivos valores p.12
Cuadro 6 Estabilidad de la relación de largo plazo para las exportaciones
| Variable | Periodo | Relaciones de largo plazoa | Pruebas de estabilidadb | |||||
| IPI USA | tcr | C | LC | F prom. | F sup. | |||
| x | 1990-2000 | 2.867 (0.070) |
0.234 (0.070) |
−11.890 (0.656) |
0.321 p = 0.200 |
5.090 p = 0.107 |
7.680 p = 0.200 |
|
| 1980-2000 | 3.597 (0.105) |
0.069 (0.100) |
−14.756 (1.046) |
0.884 p = 0.010 |
10.759 p = 0.010 |
20.371 p = 0.010 |
||
| x {−QP} | 1980-1989 | 2.917 (0.302) |
0.163 (0.123) |
−12.595 (1.351) |
0.479 p = 0.111 |
5.382 p = 0.088 |
13.884 p = 0.082 |
|
| 1991-2000 | 2.945 (0.0712) |
0.702 (0.067) |
−17.077 (0.608) |
0.258 p = 0.200 |
5.003 p = 0.114 |
10.460 p = 0.200 |
||
| x {Q} | 1980-1989 | 4.564 (0.199) |
— — |
−18.974 (0.889) |
0.772 p = 0.018 |
6.560 p = 0.010 |
12.105 p = 0.200 |
|
| 1991-2000 | 3.279 (0.074) |
— — |
−12.706 (0.353) |
0.176 p = 0.200 |
1.831 p = 0.200 |
4.897 p = 0.200 |
||
a Errores estándar entre paréntesis.
bp = valor p para el estadístico.
Lo primero que se destaca es que las elasticidades para las exportaciones totales calcula das con el método FM-LS son muy similares a las obtenidas con el método de Johansen y a las conseguidas con el modelo de corrección de error no restringido. Las pruebas de estabilidad confirman los resultados comentados en la sección II, que no mostraban evidencia de inestabilidad en la relación de largo plazo: el valor p de cada prueba estadística se encuentra por encima de 0.20.
Para las exportaciones no petroleras y sin maquila (x {−QP} ) se encontró una relación de largo plazo para los tres periodos. Sin embargo, para la muestra completa los estadísticos de prueba detectan inestabilidad. Para cada una de las dos submuestras los vectores de cointegración difieren principalmente en cuanto al coeficiente del tipo de cambio real. En este caso parece haber ocurrido un cambio estructural, pero no tan drástico como para encubrir la presencia de una relación de largo plazo. Las exportaciones de maquila ejemplifican una situación en la que el cambio en los coeficientes esconde la existencia de una relación de cointegración. Para toda la muestra no fue posible encontrar algún vector razonable, pero sí para cada submuestra.13 El tipo de cambio real no es significativo en ningún vector, y la elasticidad del índice de la producción industrial de los Estados Unidos es mayor en la primera submuestra, en que, además, los estadísticos detectan probable inestabilidad. Este problema no aparece en la segunda submuestra.
En el cuadro 7 se presentan los resultados correspondientes a las importaciones. La interpretación es la misma que en el cuadro 6. Para las importaciones totales solamente se encontró un vector de cointegración para el periodo 1991- 2000. Este es muy similar al obtenido en la sección II (en particular, el nivel exportaciones es parte del conjunto cointegrador). Para las importaciones de bienes de capital fue posible encontrar un vector de cointegración para cada periodo. Si bien el obtenido para toda la muestra y la primera submuestra indica inestabilidad, la segunda submuestra es muy estable. Tanto para este tipo de importaciones, como para las de bienes de consumo, el nivel de exportaciones no entra en la relación de largo plazo, lo cual es intuitivamente razonable. La variable de escala (el índice de la producción industrial de México) no entró en la primera submuestra. Esta es una situación en la que el cambio estructural no esconde la relación de largo plazo. El caso de las importaciones de bienes de consumo también indica un vector de cointegración inestable para toda la muestra. Sin embargo, los correspondientes a las dos submuestras son estables, particularmente el de la segunda.
Cuadro 7 Estabilidad de la relación de largo plazo para las importaciones
| Variable | Periodo | Relaciones de largo plazoa | Pruebas de estabilidadb | ||||||
| IPI USA | tcr | x | C | LC | F prom. | F sup. | |||
| m | 1991-2000 | 1.124 (0.131) |
−0.286 (0.061) |
0.461 (0.043) |
−0.676 (0.922) |
0.863 p = 0.020 |
12.054 p = 0.010 |
24.897 p = 0.010 |
|
| 1980-2000 | 2.217 (0.151) |
−1.570 (0.141) |
— — |
5.141 (1.623) |
1.518 p = 0.010 |
9.624 p = 0.010 |
22.547 p = 0.010 |
||
| m {cap} | 1980-1989 | — — |
−1.966 (0.237) |
— — |
18.300 (2.082) |
0.762 p = 0.119 |
5.561 p = 0.025 |
13.884 p = 0.071 |
|
| 1991-2000 | 1.966 (0.077) |
−0.734 (0.068) |
— — |
−0.927 (0.728) |
0.173 p = 0.200 |
2.658 p = 0.200 |
9.215 p = 0.200 |
||
| 1980-2000 | 3.506 (0.376) |
−2.277 (0.350) |
— — |
4.720 (4.039) |
0.962 p = 0.010 |
9.488 p = 0.010 |
17.121 p = 0.023 |
||
| m {cons} | 1980-1989 | 5.324 (1.571) |
−2.188 (0.402) |
— — |
−4.095 (8.802) |
0.696 p = 0.035 |
5.818 p = 0.066 |
14.974 p = 0.054 |
|
| 1991-2000 | 1.753 (0.150) |
−1.160 (0.132) |
— — |
3.30677 (1.411) |
0.086 p = 0.200 |
1.537 p = 0.200 |
7.990 p = 0.200 |
||
| m {int} | 1991-2000 | — — |
−0.476 (0.048) |
0.908 (0.017) |
4.261 (0.399) |
0.331 p = 0.200 |
4.806 p = 0.129 |
10.862 p = 0.200 |
|
| m {int_−QP} | 1991-2000 | — — |
−0.206 (0.071) |
1.224 (0.026) |
−0.181 (0.592) |
0.567 p = 0.067 |
10.247 p = 0.010 |
20.327 p = 0.010 |
|
| 1980-2000 | 2.549 (0.502) |
−0.719 (0.186) |
0.036 (0.182) |
−2.833 (2.923) |
1.388 p = 0.010 |
11.626 p = 0.010 |
19.623 p = 0.264 |
||
| m {int_−QP} | 1991-2000 | 1.200 (0.158) |
−0.146 (0.074) |
0.323 (0.053) |
−2.523 (1.118) |
1.000 p = 0.010 |
10.014 p = 0.010 |
15.524 p = 0.113 |
|
a Errores estándar entre paréntesis.
bp = valor p para el estadístico.
Para las importaciones de bienes intermedios sólo se encontró cointegración para la segunda submuestra. El vector de cointegración fue muy estable y no incluye al índice de la producción industrial pero sí al nivel de las exportaciones. En realidad, al desagregar los datos aún más se encontró que las importaciones para la industria de maquila solamente presentan una relación de cointegración inestable en la segunda submuestra. Para los bienes intermedios importados de la industria no maquiladora se encontró cointegración para ambas submuestras pero no para todo el periodo. La estabilidad en estos casos no es obvia, puesto que los resultados de las pruebas son contradictorios (una de ellas sugiere estabilidad y las otras dos rechazan esta hipótesis).
Las conclusiones de esta sección pueden sintetizarse como sigue. Primero, para todo el periodo 1980-2000 no es posible encontrar una relación de cointegración para cada uno de los tipos de importaciones y exportaciones que aquí se analizan. Sin embargo, para la mayor parte de las categorías se encontraron relaciones de largo plazo estables para el periodo 1990-2000. Las únicas excepciones parecen ser los datos a nivel muy desagregado para las importaciones de bienes intermedios. Finalmente, en la gráfica 8 se muestra con una línea continua el logaritmo de las exportaciones no petroleras y su nivel de largo plazo construido en partes (donde una ecuación diferente ajusta cada segmento de la muestra) y en que no se incorporan ni la dinámica de corto plazo (rezagos) ni factores estacionales. Es notorio que con el paso del tiempo el nivel de las exportaciones parece ser más volátil alrededor de su tendencia de largo plazo.
IV. Modelos de corrección de error
En esta sección se analizan las propiedades estadísticas de los modelos de corrección de error asociados a las relaciones de largo plazo para el periodo 1990-2000. Los términos de corrección de error se construyen con los coeficientes de los cuadros 6 y 7. Los cuadros siguientes muestran los estimados de los parámetros de corto plazo y, al final, varios estadísticos de prueba. Una variable con superíndice x i = x, x {−QP} , x {Q} indica que ésta debe ser entendida como específica a una ecuación dada. El cuadro 8 contiene los resultados para las exportaciones.
Cuadro 8 Modelos de corrección de error para las exportaciones
| Variable | Modelos | ||
|
|
|
|
|
|
|
−0.314 (0.077) |
−0.271 (0.085) |
−0.592 (0.123) |
|
|
−0.420 (0.085) |
−0.483 (0.081) |
−0.444 (0.102) |
|
|
−0.237 (0.078) |
−0.358 (0.073) |
−0.30300 (0.082) |
|
|
−0.231 (0.075) |
||
|
|
−0.294 (0.077) |
||
|
|
−0.225 (0.072) |
||
|
|
−0.161 (0.062) |
||
|
|
−0.304 (0.075) |
||
|
|
−0.245 (0.071) |
−0.358 (0.069) |
−0.214 (0.062) |
|
|
−0.417 (0.121) |
||
|
|
−2.222 (0.897) |
||
| Est. MCE | −6.380 | −4.800 | −4.880 |
| R 2 | 0.769 | 0.713 | 0.839 |
| R 2 ajustada | 0.728 | 0.679 | 0.812 |
| E. E. | 0.045 | 0.053 | 0.051 |
| Coeficiente asimetría | 0.154 | 0.226 | −0.072 |
| Curtosis | 3.472 | 3.583 | 2.656 |
| Est. Jarque-Bera | 1.680 | 2.587 | 0.662 |
| LM 12 AR | 1.387 | 0.728 | 0.771 |
| LM 12 ARCH | 0.970** | 0.627 | 0.786 |
| Prueba de White | 1.502* | 0.030 | 1.019 |
| RESET | 0.002 | 0.013 | 0.474 |
| Chow B. (94:01) | 1.016 | 0.793 | 1.901** |
| Chow Pred. (94:01) | 1.224 | 0.839 | 0.967 |
Los coeficientes de velocidad de ajuste14 son todos negativos y muy significativos, lo que fortalece la hipótesis de existencia de una relación de largo plazo. En todos los casos el valor es muy alto, lo que indica que el proceso de ajuste no toma mucho tiempo para ser completado. Hay varios rezagos de la variable dependiente, principalmente negativos, y eso produce un oscilante proceso de ajuste. En el caso de las exportaciones totales, los coeficientes relativos al cambio en la actividad económica de los Estados Unidos son muy altos. El efecto de corto plazo de variaciones en el tipo de cambio real aparece solamente en la ecuación de las exportaciones sin petróleo y sin maquila.
Todos los estadísticos ECM (obtenidos con el modelo no restringido) son significativos a 1%. Las medidas de bondad de ajuste son muy buenas. No hay problemas con la normalidad de los residuales y solamente la ecuación para las exportaciones totales muestra alguna evidencia de efectos ARCH. Las pruebas de Chow de quiebre estructural y falla de pronóstico para enero de 1994 son todas no significativas, con la excepción de un caso. Se introdujo una variable igual a 1 al comienzo de 1994 y ésta fue no significativa.
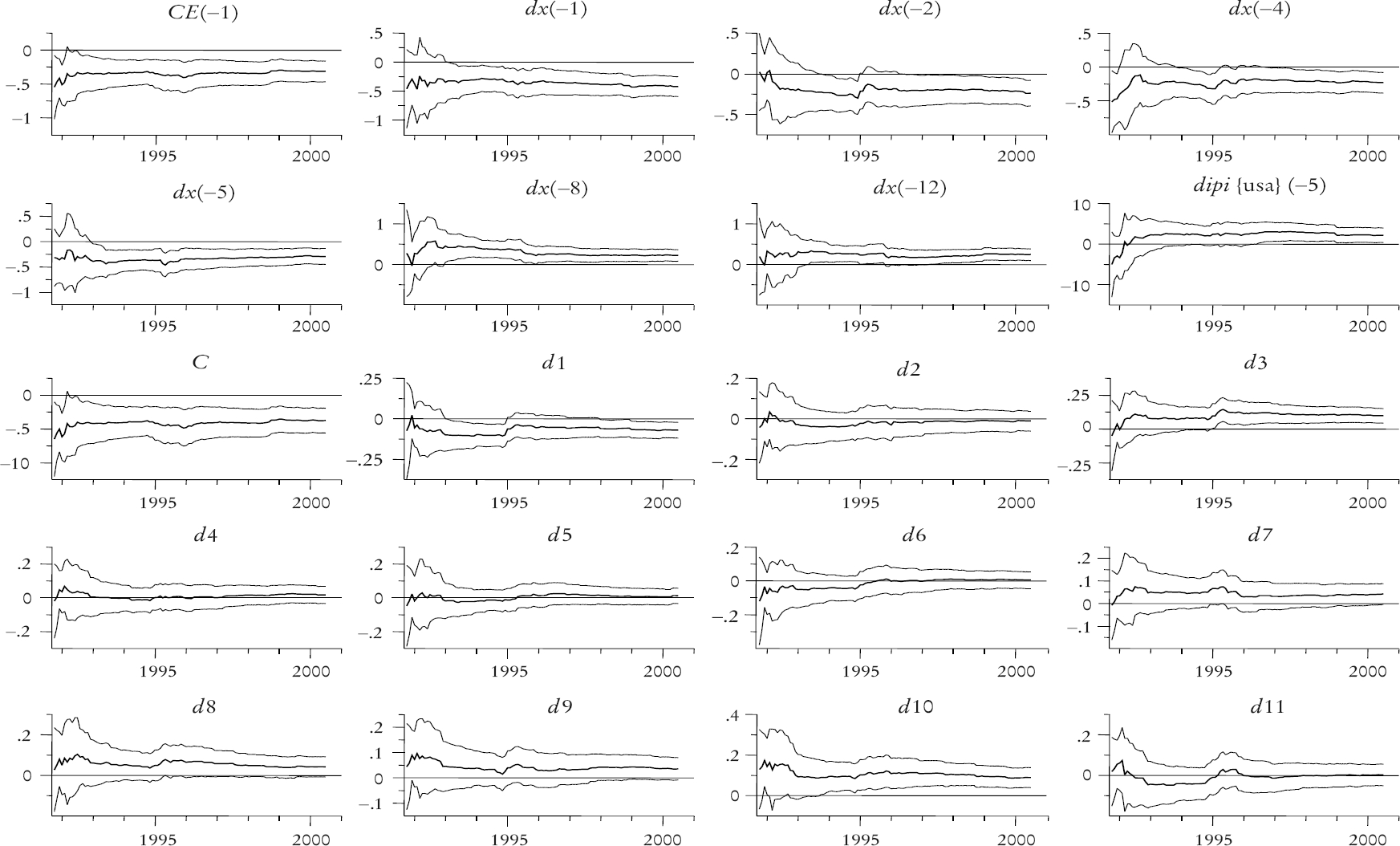
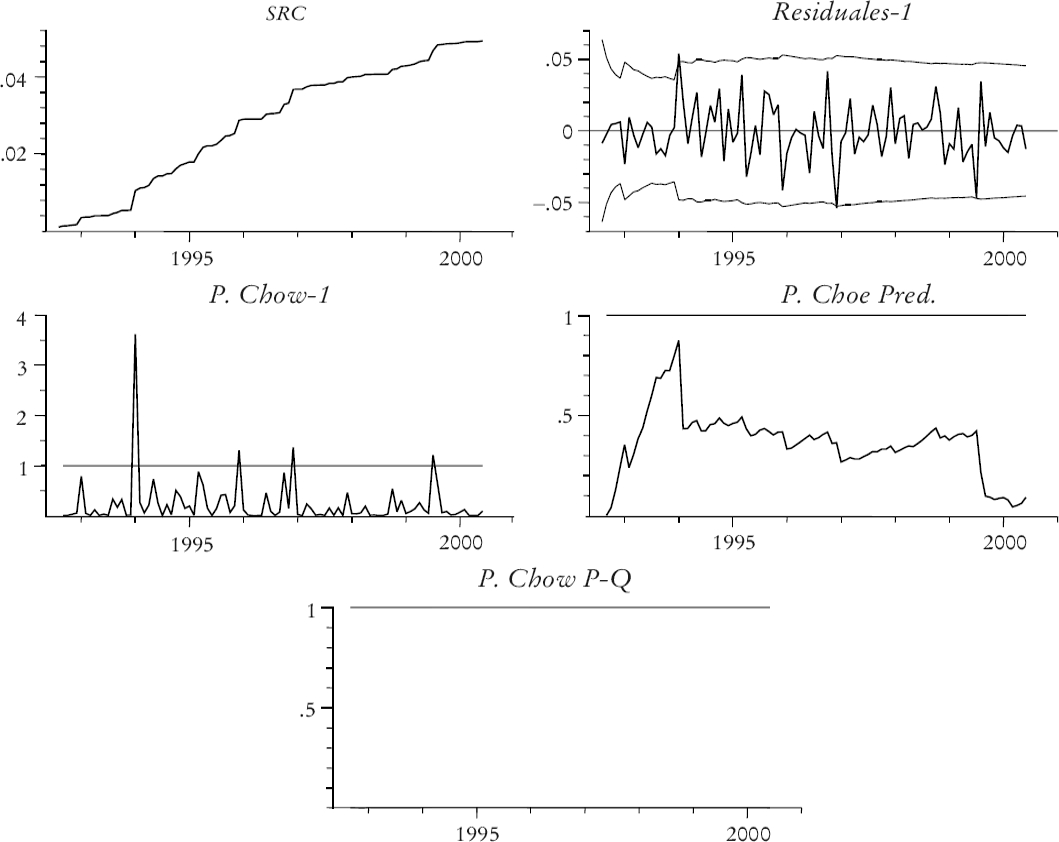
En la gráfica 9 se presenta el análisis recursivo de los modelos de corrección de error para las exportaciones totales. La primera parte muestra la suma de cuadrados, la cual se aproxima a una línea recta; la segunda parte muestra la secuencia de residuales de un paso adelante que cruza la banda de confianza solamente en un mes. La siguiente parte muestra los estadísticos de Chow que solamente detectan tres casos de observaciones extremas al tiempo de la crisis de 1995. Las últimas dos partes muestran los estadísticos de n pasos hacia adelante y n pasos hacia atrás de cambio estructural de Chow. En ambos casos la secuencia permanece debajo de la línea de significación al 5%. En la gráfica 10 se muestra la secuencia de coeficientes recursivos para el mismo modelo de corrección de error. Cabe señalar que las secuencias para las variables ficticias (dummies) estacionales también están incluidas. Se puede observar que los coeficientes de corto plazo también son relativamente constantes. En el cuadro 9 se presentan los resultados para las importaciones y contiene el mismo conjunto de estadísticos que el cuadro 8.
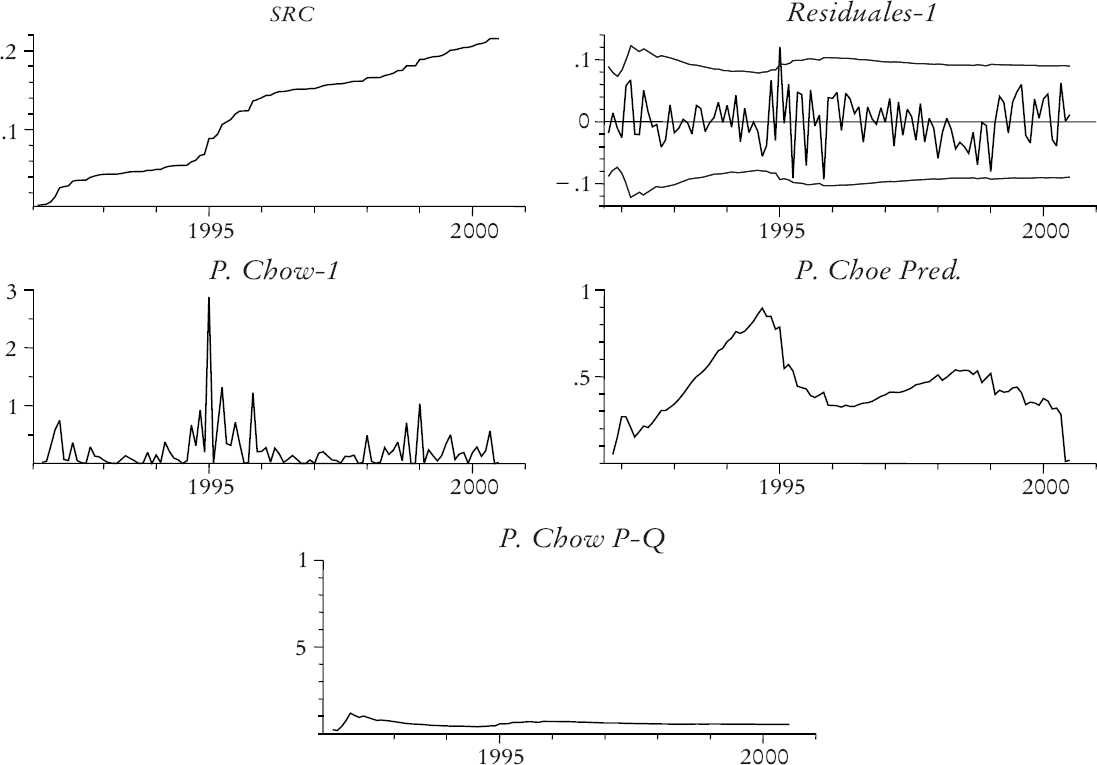
Gráfica 9 Pruebas recursivas de estabilidad para los modelos de corrección de error para las exportaciones totales
Cuadro 9 Modelos de corrección de error para las importaciones
| Variable | Modelos | |||||
|
|
|
|
|
|
|
|
|
|
−0.246 (0.057) |
−0.343 (0.076) |
−0.323 (0.063) |
−0.313 (0.069) |
−0.277 (0.080) |
−0.331 (0.064) |
|
|
−0.214 (0.067) |
−0.440 (0.082) |
||||
|
|
−0.447 (0.089) |
|||||
|
|
−0.374 (0.093) |
|||||
|
|
−0.26300 (0.078) |
|||||
|
|
−0.195 (0.064) |
|||||
|
|
0.101 (0.035) |
|||||
|
|
−0.139 (0.037) |
−1.888 (0.060) |
−0.130 (0.060) |
|||
|
|
0.78300 (0.043) |
0.914 (0.048) |
1.00600 (0.088) |
0.510 (0.054) |
||
|
|
0.670 (0.091) |
1.605 (0.201) |
1.772 (0.205) |
1.221 (0.122) |
||
|
|
−0.487 (0.156) |
|||||
|
|
−0.199 (0.057) |
−0.412 (0.161) |
−0.218 (0.076) |
−0.370 (0.077) |
||
|
|
0.175 (0.072) |
|||||
|
|
0.342 (0.101) |
|||||
| Est. MCE | −5.460 | −6.850 | −5.200 | −6.370 | −4.810 | −6.820 |
| R 2 | 0.942 | 0.740 | 0.813 | 0.903 | 0.901 | 0.892 |
| R 2 ajustada | 0.932 | 0.705 | 0.787 | 0.888 | 0.881 | 0.875 |
| E. E. | 0.023 | 0.067 | 0.069 | 0.029 | 0.040 | 0.031 |
| Coeficiente asimetría | −0.095 | 0.056 | 0.239 | −0.335 | −0.103 | −0.427 |
| Curtosis | 3.617 | 2.890 | 3.484 | 3.514 | 2.440 | 3.144 |
| Est. Jarque-Bera | 1.959 | 0.130 | 2.430 | 3.390 | 1.691 | 3.537 |
| LM 12 AR | 1.555 | 1.533 | 0.839 | 0.695 | 1.042 | 1.106 |
| LM 12 ARCH | 0.701 | 0.779 | 0.888 | 1.096 | 0.919 | 0.540 |
| Prueba de White | 1.065 | 0.956 | 1.459 | 1.169 | 1.570* | 0.72 |
| RESET | 0.074 | 2.453 | 0.033 | 0.089 | 2.456 | 2.452 |
| Chow B. (94:01) | 2.113** | 1.183 | 1.201 | 2.209** | 1.913** | 1.850** |
| Chow Pred. (94:01) | 1.782* | 0.533 | 0.625 | 0.938 | 1.271 | 0.999 |
Los coeficientes de velocidad de ajuste para las importaciones también implican convergencia rápida. La presencia de términos de corto plazo refuerza esta propiedad. Los estadísticos ECM son todos significativos a 1%. Las medidas de bondad de ajuste son similares a las encontradas para las exportaciones. No existen problemas con los residuales. Las pruebas RESET son fácilmente superadas en todos los casos. Sin embargo, solamente las ecuaciones para bienes de consumo y bienes de capital pasan las pruebas de Chow. El rechazo de la estabilidad con ambas pruebas ocurre sólo en cuanto a las importaciones totales.
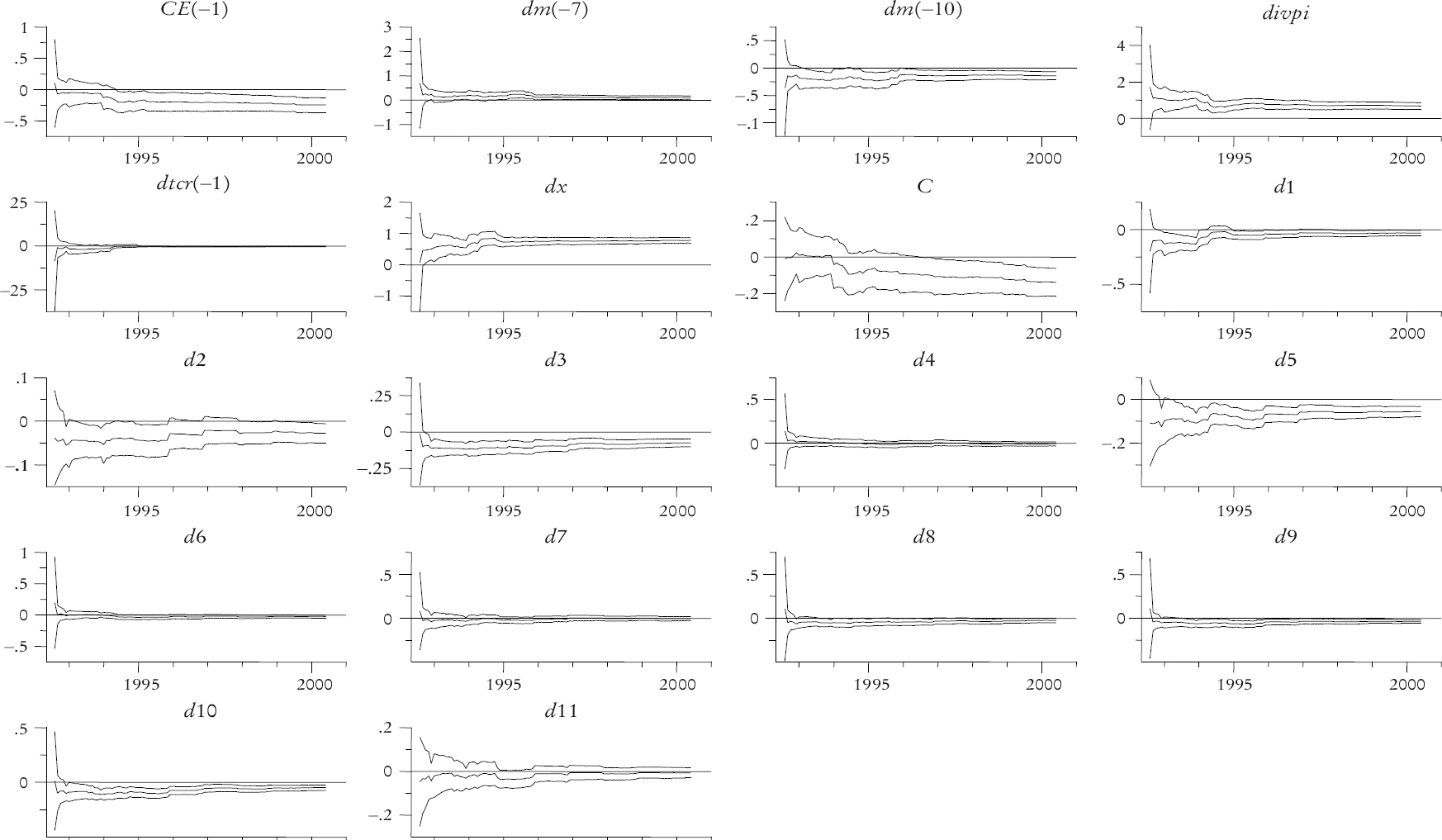
En la gráfica 12 se completó el análisis del modelo de corrección de error para las importaciones totales. En las partes se presentan los estadísticos recursivos. La suma de residuales se aproxima a una línea recta. Los residuales de un paso permanecen dentro de las bandas excepto en un mes. La secuencia de estadísticos de Chow de un paso muestra más observaciones extremas que en el caso de las exportaciones. Sin embargo, los estadísticos de Chow de n pasos no señalan problema alguno. Para completar el análisis, en la gráfica 11 se muestran las secuencias de estadísticos recursivos para el mismo modelo, los cuales parecen ser constantes a lo largo de todo el periodo de muestra.
V. Análisis de la estabilidad de las funciones de importaciones y exportaciones
De los resultados anteriores se puede concluir que aunque es fácil en general obtener funciones de importaciones, para las exportaciones es más complicado si la muestra es larga. Entre las razones para ello se puede plantear que hubo un cambio estructural pero esta no es la única posibilidad. En esta sección se proporciona un resultado adicional que sugiere que el cambio estructural, aunque probable, no forzosamente está detrás de la inestabilidad de la función de exportaciones en una muestra larga.
Bleaney (1999) mediante un análisis de panel de datos tanto para exportaciones manufactureras como totales encuentra que las reformas comerciales efectuadas en la América Latina de 1979 a 1994 tuvieron el efecto de aumentar las elasticidades ingreso y tipo de cambio real mientras que la tasa de crecimiento del PIB y la tasa de inversión no parecen haber sido afectadas. En particular, en sus estimaciones la elasticidad ingreso se incrementó entre .87 y 1.12.
Estos hallazgos coinciden parcialmente con los encontrados para la función de exportaciones no maquiladores que excluyen petróleo. En efecto, los datos del cuadro 6 muestran que la elasticidad ingreso pasa de 2.92 en el periodo 1980-1989 a 2.93 para la otra parte de la muestra. El aumento aunque del mismo signo que el encontrado por Bleaney es, no obstante, muy pequeño. Por lo contrario, la elasticidad para el tipo de cambio real experimenta un cambio mucho mayor al pasar de 0.16 a 0.70, más en línea con lo presentado por dicho autor.
En un artículo más reciente Santos-Paulino y Thirlwall (2004) usan una muestra más extensa de países en desarrollo de diversos continentes aplicando también la técnica de panel de datos y estudian tanto las funciones de exportaciones como de importaciones. Sus resultados indican que la liberación comercial tuvo un efecto en la promoción de las exportaciones pero el efecto en las importaciones fue aún mayor, con lo cual las balanzas de pago tendieron a deteriorarse aunque el efecto neto en crecimiento parece haber sido positivo.
Así, parece que los hallazgos de la bibliografía del tema coincide con la explicación de que cambios en las políticas de comercio producen cambios en los parámetros de las funciones de exportación. Sin embargo, se debe tener en cuenta que los resultados con análisis de panel de datos, aunque ilustrativos para ciertos propósitos, no pueden ser aplicados de manera mecánica para interpretar los datos individuales de los países incluidos (véase Maddala y Kim, 1998). En este sentido, los resultados obtenidos por nuestros análisis de series de tiempo no son completamente comparables con los obtenidos por estos otros trabajos basados en paneles de datos. Por esta razón no se descarta del todo la posibilidad de que el cambio estructural en México haya sido de menor intensidad que el sugerido por estos trabajos y que la inestabilidad entre submuestras comentada líneas arriba sea motivada por algún cambio metodológico en la elaboración de los datos. Esto sería congruente con que los cambios en las elasticidades ingreso son relativamente menores y que los problemas para obtener funciones de exportaciones sean más severos en el caso de la maquila, en la que hubo un importante cambio metodológico a principios de los años noventa.
Conclusiones
El comercio exterior mexicano ha tenido un notorio desempeño desde la segunda mitad de los años noventa; respecto a las exportaciones han triplicado su tasa de crecimiento y fueron las más vigorosas en todo el mundo durante el periodo examinado. Se estimaron funciones de importaciones y exportaciones de largo plazo para el periodo 1990-2000 y se obtuvieron coeficientes que tienen los signos y magnitudes apropiadas. Se encontró que la ecuación de exportaciones, como una función del índice de la producción industrial de los Estados Unidos y el tipo de cambio real, es sumamente estable para dicho periodo. La demanda de importaciones totales, como función del índice de la producción industrial de México, del tipo de cambio real y de las exportaciones, muestra inestabilidad para el mismo periodo. No obstante, la ecuación de largo plazo ajusta los datos bastante bien aun sin considerar la estacionalidad ni la dinámica de corto plazo.
El análisis se extendió a los datos desagregados para el periodo 1980-2000. Se demostró que solamente en unos pocos casos se puede encontrar un vector de cointegración para toda la muestra aunque, de acuerdo con las pruebas de Hansen (1992) para regresiones con variables I(1), ninguno de ellos fue estable. Sin embargo, en casi todos los casos, excepto uno, se encontró un vector de cointegración estable para el subperiodo 1990-2000. Para la mayoría de los casos un vector de cointegración también fue encontrado para la submuestra 1980-1989, aunque ese vector no muestra la estabilidad característica del segundo segmento de la muestra. También se obtuvieron modelos de corrección de error para el periodo 1990-2000 y se encontró que éstos eran muy estables.
Por último, se analizó la relación de los hallazgos de este documento con otros registrados para otros países. Los cambios en las elasticidades en la función de exportaciones están en línea con lo encontrado en otros países en lo que respecta al signo (es decir, hay un aumento de las elasticidades después de las reformas comerciales), pero son considerablemente menores en magnitud, por lo cual el cambio estructural podría no haber sido tan drástico como en otros países estudiados en la bibliografía.











 nueva página del texto (beta)
nueva página del texto (beta)