Clasificación JEL: O10, O40, R1.
Introducción
Estudios recientes afirman que las reformas comerciales de México causaron un aumento de las disparidades regionales. Chiquiar (2005) y Rodríguez y Sánchez (2002) muestran que tanto la β como la σ convergencia desaparecen después de la liberación económica, ya que estiman una relación positiva entre la tasa de crecimiento del ingreso y el ingreso inicial per capita después de 1985, lo que interpretan como evidencia de divergencia. Además, después de incluir variables económicas adicionales (como los años promedio de escolaridad, el porcentaje de cierta actividad económica en relación con el producto estatal bruto (PEB), indicadores de infraestructura, inversión estatal y Federal, etc.) para tener en cuenta la posibilidad de que las regiones no compartan el mismo estado estacionario,1 pueden identificar las características que permiten a las regiones ricas crecer más rápidamente que las pobres.
Por nuestra parte, estudiamos la dinámica del crecimiento regional con base en una metodología de series de tiempo (a partir de aquí τ convergencia). Esto nos permite llegar a conclusiones que no son accesibles con la metodología de Barro y Sala-i-Martin. Primero, la noción de convergencia con datos de corte transversal es más débil que la de τ convergencia; la evidencia de una relación negativa entre las tasas de crecimiento y los ingresos iniciales no puede to mar se como prueba de convergencia en el ingreso; en cambio, sólo trasmite la idea de “acercamiento sistemático” (catching-up, en inglés; véase Andrew y Durlauf, 1996). Segundo, es posible analizar el patrón del ingreso regional durante un extenso periodo, y no obstante, enfocarse en un subperiodo específico. Esto ofrece la oportunidad de analizar la pauta de crecimiento para el intervalo 1940-2003 y compararlo con el subperiodo 1985-2003. Tercero, este método ofrece una visión más detallada respecto a la experiencia de regiones particulares, dado que con esta metodología se analiza la diferencia en el ingreso per capita entre dos economías, podemos identificar las características individuales de la dinámica del crecimiento para cada región.
Los resultados sugieren que la diferencia en el ingreso per capita en el periodo 1940-2003 tiende a reducirse en el transcurso del tiempo con respecto a la región Capital. No obstante, el desarrollo regional fue cuantitativamente heterogéneo entre las regiones. Encontramos evidencia que apoya la hipótesis de que las reformas comerciales afectaron negativamente a las regiones pobres; se muestra que, a partir de entonces, las diferencias entre el ingreso de la región Capital y algunas de las regiones más pobres de México se acentuaron; además, no existe evidencia para afirmar que las reformas comerciales contribuyeron a igualar el ingreso per capita entre las regiones fronterizas de México y de los Estados Unidos.
El artículo está organizado de la siguiente manera. En la sección I se revisa brevemente la metodología de convergencia usando datos de corte transversal y presenta evidencia en este sentido para las regiones mexicanas durante el periodo 1985-2003. En la sección II se explica la metodología usa da para estudiar la hipótesis de la convergencia con series de tiempo y se analiza casos que no han si do considerados todavía en la bibliografía del tema; también se informa de los resultados de las pruebas usan do las técnicas de series de tiempo trabajadas en pares y, finalmente, se consideran sus consecuencias para las diferentes regiones de México. En la sección III se analiza si la liberación comercial contribuye a la convergencia del ingreso per capita entre las regiones fronterizas de México y los Estados Unidos. Al final se re sume las conclusiones principales.
I. Análisis con datos de corte transversal
1. Metodología
La mayoría de las pruebas empíricas concernientes a la hipótesis de convergencia emplea datos de corte transversal usando el modelo de crecimiento neoclásico como teoría subyacente (Barro y Sala-i-Martin, 2004; Cárdenas y Pontón, 1995; Chiquiar, 2005). El modelo de crecimiento neoclásico implica convergencia condicional del ingreso per capita: la tasa de crecimiento del ingreso per capita disminuye a medida que la economía se aproxima al estado estacionario. Si un grupo de economías comparte un estado estacionario común, el modelo implica la convergencia absoluta en el ingreso per capita: las economías más pobres crecen más rápido que las ricas. Barro y Sala-i-Martin (2004) usan la ecuación 1 para probar si existe β convergencia; derivan ésta del modelo de Ramsey después de log-linealizar las ecuaciones diferenciales en torno del estado estacionario.
en que se supone que α es homogénea para todas las regiones y su valor depende de los parámetros tecnológicos del modelo; el parámetro β mide la velocidad de la convergencia hacia el estado estacionario común, y i,0 representa el ingreso inicial per capita de la región i y y i,T denota el ingreso final per capita. La estimación del parámetro β positivo (negativo) es evidencia de convergencia (divergencia) regional. Se estima la ecuación 1 usando mínimos cuadrados no lineales (MCNL).
2. Análisis por estado
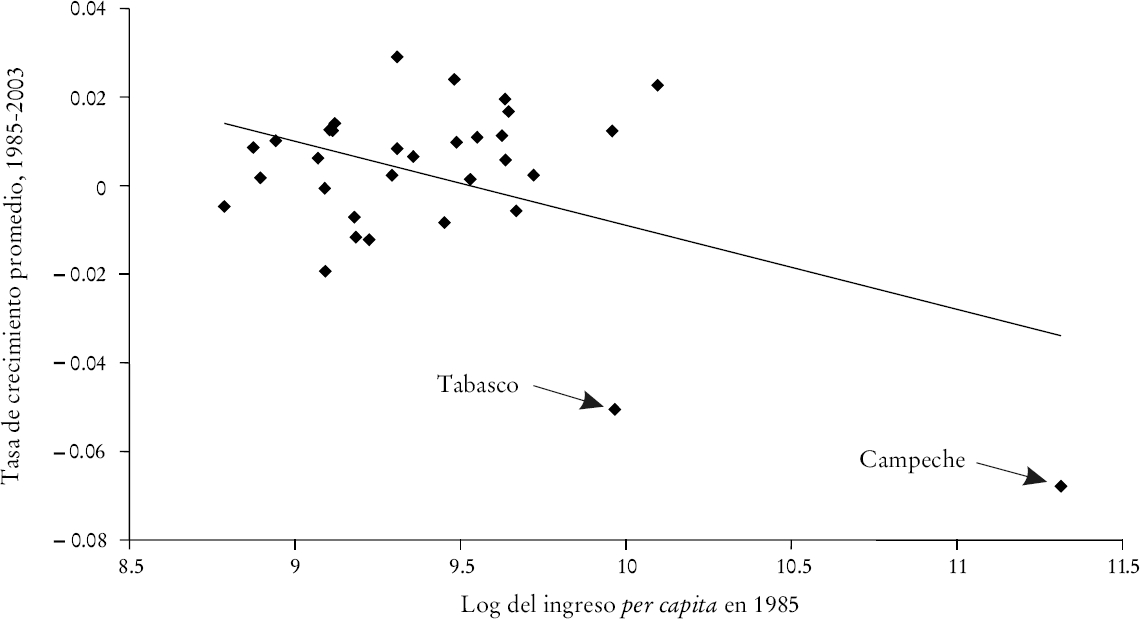
Los datos del ingreso per capita2 para 1985, 1988, 1994 y 2003 usados en esta sección se obtuvieron del BIE3 proporcionado por el INEGI.4 En la gráfica 1 se presenta la tasa de crecimiento promedio para el periodo 1985-2003 con respecto al logaritmo del ingreso inicial per capita. La relación negativa entre es tas dos variables sugiere convergencia absoluta entre los estados mexicanos.
Estudios relacionados afirman que Campeche y Tabasco pueden sesgar el análisis de convergencia, pues una parte considerable de su PEB se genera por medio de la explotación de reservas petroleras. De hecho, su exclusión conduce a una visión algo diferente del proceso de crecimiento del ingreso per capita después de 1985. Como se muestra en la gráfica 2, hay una relación positiva entre las tasas de crecimiento observadas y el ingreso inicial, lo que se interpreta como evidencia de divergencia de acuerdo con la metodología de Barro y Sala-i-Martin.
Esquivel (1999) encuentra evidencia de convergencia del ingreso per capita para el periodo 1940-1995. No obstante, los resultados sugieren que el proceso de convergencia no fue homogéneo: de 1940 a 1960 la tasa estimada a la que los estados pobres se aproxima ron a los estados ricos fue de 2.23% al año; de 1960 a 1980 ésta disminuyó a 1.4%, en tanto que de 1980 a 1995 la tasa estimada no fue significativamente diferente de 0. La gráfica 2 sugiere que la dinámica de la tasa de crecimiento se invierte, y que los estados ricos crecieron más rápidamente que los pobres.
Dispersión del ingreso per capita (σ convergencia). Para completar el análisis de β convergencia calcula mos la desviación estándar del ingreso per capita. De acuerdo con Barro y Sala-i-Martin (2004), se considera que un valor bajo (alto) de esta medida es evidencia de σ convergencia (divergencia). En la gráfica 3 se muestra que la evolución de la dispersión del ingreso depende de los estados que se incluyan en el cálculo: cuando todos los estados son considerados, las disparidades disminuyen durante el periodo 1985-2003; con sólo 30 estados, las disparidades aumentan rápidamente después de 1985, y, después de 1988, aumentan con más lentitud. Estos hechos son congruentes con la información presentada en las gráficas 1 y 2. De 1994 a 2003 la dispersión del ingreso se comporta de manera similar, independientemente de la muestra que se use.
3. Análisis por región
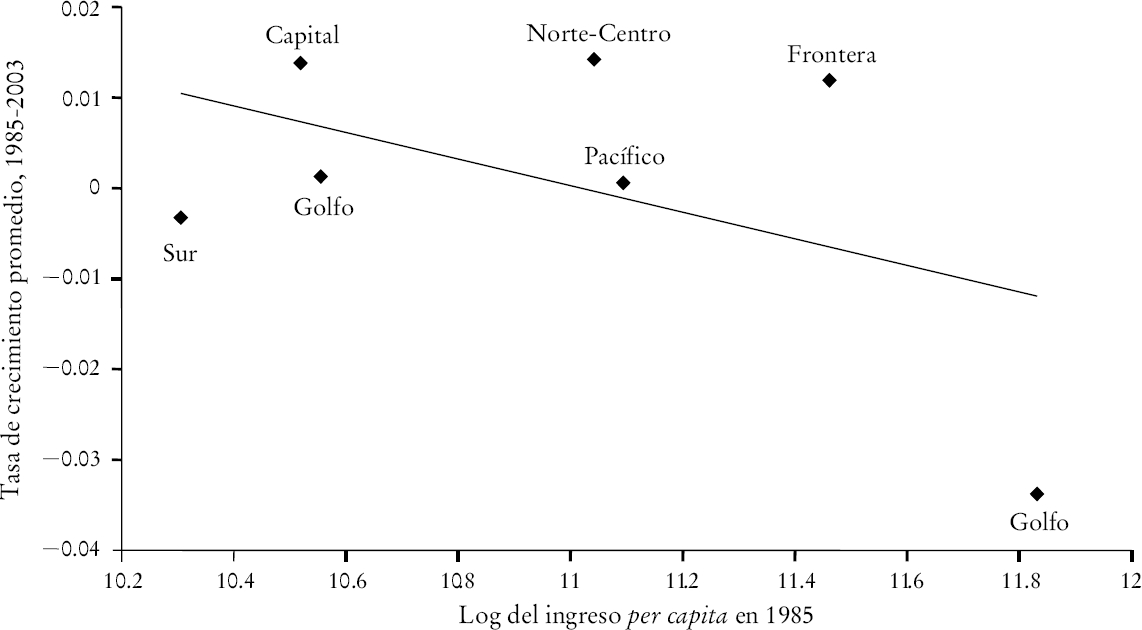
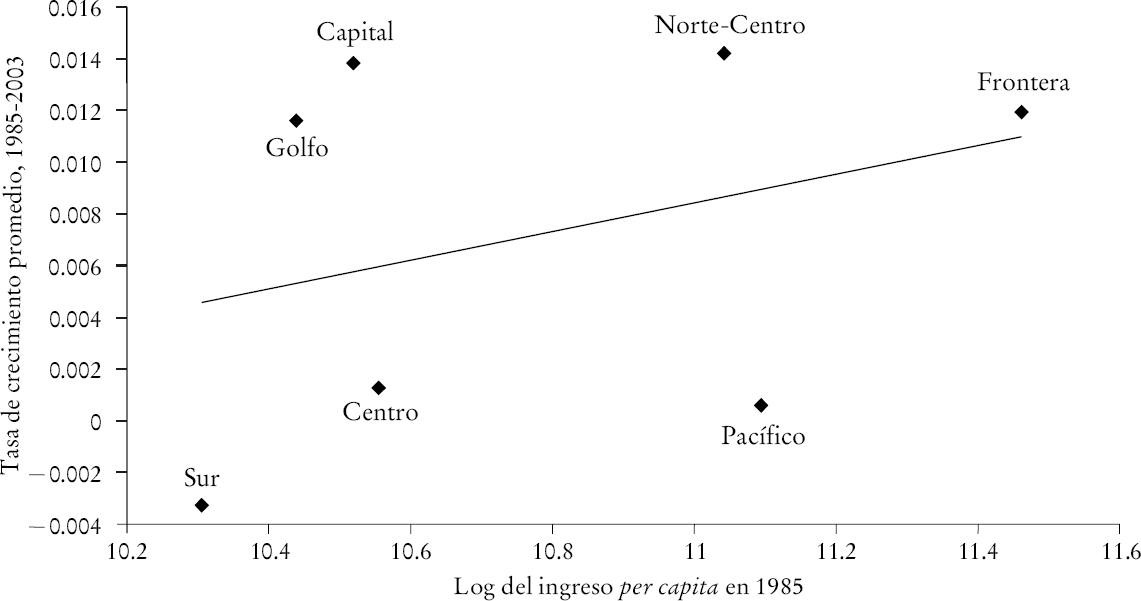
En esta subsección se analiza el proceso de crecimiento basado en grupos de estados. Definimos estas regiones con base en Esquivel (1999). Cada uno de los estados está incluido en una de las siete regiones descritas en el cuadro 1. Las gráficas 4 y 5 muestran la tasa de crecimiento promedio respecto al ingreso inicial. Como en el caso del análisis por estado, aquí hay evidencia de convergencia cuando se incluye a todos los estados; sin embargo, cuando se excluye a Campeche y Tabasco de la región Golfo se encuentra evidencia de divergencia.
Cuadro 1 Regiones
| Región | Estado | |
| 1 | Capital | Distrito Federal y Estado de México |
| 2 | Centro | Hidalgo, Morelos, Puebla y Tlaxcala |
| 3 | Norte-Centro | Aguascalientes, Durango, Guanajuato, Querétaro, San Luis Potosí y Zacatecas |
| 4 | Golfo | Campeche, Quintana Roo, Tabasco, Veracruz y Yucatán |
| 5 | Frontera | Baja California, Chihuahua, Coahuila, Nuevo León, Sonora y Tamaulipas |
| 6 | Pacífico | Baja California Sur, Colima, Jalisco, Nayarit y Sinaloa |
| 7 | Sur | Chiapas, Guerrero, Michoacán y Oaxaca |
4. Estimación de la tasa de convergencia
El cuadro 2 resume las estimaciones de MCNL del parámetro β usando la ecuación 1. Las conclusiones obtenidas de estos resultados concuerdan con las obtenidas mediante el análisis gráfico. Los valores estimados varían dependiendo de la muestra y del periodo de tiempo analizados. Existe evidencia de convergencia cuando se calcula β usando la muestra completo. La parte A del cuadro 2 muestra una estimación del parámetro β positiva y estadísticamente significativa para el periodo 1985-2003 y el subperiodo 1985-1994. Se encuentra evidencia de divergencia sólo cuando se excluyen Campeche y Tabasco; la par te B muestra una estimación negativa de la tasa de convergencia para el periodo 1985-2003 y el subperiodo 1985-1994.
Cuadro 2 Estimación de la tasa de convergencia
| A. Todos los estados | B. Sin Campeche y Tabasco | ||||||
| 1985-2003 | 1985-1994 | 1994-2003 | 1985-2003 | 1985-1994 | 1994-2003 | ||
| β | 0.0232 | 0.0438 | −0.0021 | −0.0109 | −0.0207 | −0.0022 | |
| Valor P | (0.028) | (0.019) | (0.580) | (0.043) | (0.025) | (0.580) | |
| R 2 | 0.21 | 0.23 | 0.01 | 0.12 | 0.58 | 0.01 | |
| Muestra | 32 | 32 | 32 | 30 | 30 | 30 | |
Las estimaciones para el segundo subperiodo (1994-2003) son similares en ambas partes: la β estimada parece ser no significativa estadísticamente. La ausencia de evidencia en favor de convergencia o de divergencia sugiere que las disparidades del ingreso se mantuvieron relativamente estables en esta etapa. Estos resultados son similares a los que presenta Chiquiar (2005). Resulta poco satisfactorio que la inferencia de los análisis anteriores de penda de la muestra empleada; en consecuencia, cualquier conclusión que se obtenga debe considerar se subjetiva. No obstante, podemos decir que, independientemente del patrón de convergencia o divergencia, el proceso es más fuer te durante el subperiodo 1985-1994.
II. Análisis con series de tiempo
Los especialistas en series de tiempo sostienen que el análisis de τ convergencia es más completo; argumentan que la existencia de una correlación negativa entre la tasa de crecimiento y el ingreso inicial —estudios con datos de corte transversal— no deben to mar se como evidencia de convergencia, sino más bien de acercamiento sistemático (catching-up; véase Andrew y Durlauf, 1996). La convergencia de largo plazo implica que la disminución de la disparidad en el ingreso per capita entre dos economías ha terminado, es decir, la diferencia en el ingreso es estable en el tiempo. Lo anterior puede relacionarse con la bien conocida propiedad estadística de estacionariedad.
1. Metodología
La metodología básica empleada es la de Dickey-Fuller aumentada (ADF). Con esta prueba analizamos las propiedades de la diferencia logarítmica del ingreso real per capita entre dos economías determinadas (véase, por ejemplo, Li y Papell, 1999; Lee, Lim y Azali, 2005; Oxley y Greasley, 1995, entre otros). La hipótesis de convergencia puede estudiarse por medio de este enfoque estimando el siguiente modelo básico.
en el que la variable (y i,t − y j,t ) es la diferencia logarítmica en el ingreso per capita entre las economías i y j en el periodo t, y T representa una tendencia determinista. La bibliografía del tema considera los siguientes resultados.
i) Acercamiento sistemático (catching-up) (convergencia estocástica): si β < 0 y α < 0, la serie (y i,t − y j,t ) es estacionaria alrededor de una tendencia determinista negativa, es decir, hay una tendencia a que la diferencia en el ingreso per capita disminuya con el paso del tiempo.
ii) Convergencia de largo plazo (convergencia determinista): si β = 0 y α < 0, las series y i y y j están cointegradas, esto es, las reducciones en las diferencias en el ingreso per capita han terminado y se mantienen estables en el tiempo.
iii) Divergencia: si β = 0 y α = 0, la disparidad en los ingresos sigue una caminata aleatoria, es decir, la diferencia en el ingreso per capita es impredecible.
Además de estos tres resultados posibles, consideramos un resultado más, que no se ha tenido en cuenta en los escritos respecto al tema. Una noción más débil que catching-up, loose catching-up (acercamiento errático), sugiere que la economía j está alcanzando erráticamente, pero también inexorablemente, a la economía i. Esta conclusión surge si la serie en análisis contiene una tendencia negativa determinista y una estocástica de manera simultánea. Como bien se conoce, una tendencia determinista siempre domina a la estocástica (Hasseler, 2000); por tanto, encontrar evidencia de ambas indica una reducción inevitable en la diferencia en el ingreso en el largo plazo.
iv) Acercamiento errático (loose catching-up): si β < 0 y α = 0, la diferencia en el ingreso está disminuyen do, pero de una manera errática.
2. Resultados empíricos de convergencia con series de tiempo
Usamos el PEB estimado por Germán-Soto (2005) para el periodo 1940-2003. Ya que hay 32 estados y que la prueba se realiza por pares, se necesita ría mucho tiempo para analizar la disparidad en el ingreso estado por estado. Por tanto, se hace el análisis de τ convergencia usando las regiones previamente definidas. Concretamente, comparamos el proceso de crecimiento entre la región Capital y el resto de las regiones descritas en el cuadro 1. Usamos a la región Capital para nuestra comparación, pues esta es la región con el mayor ingreso per capita en todo el periodo de la muestra.
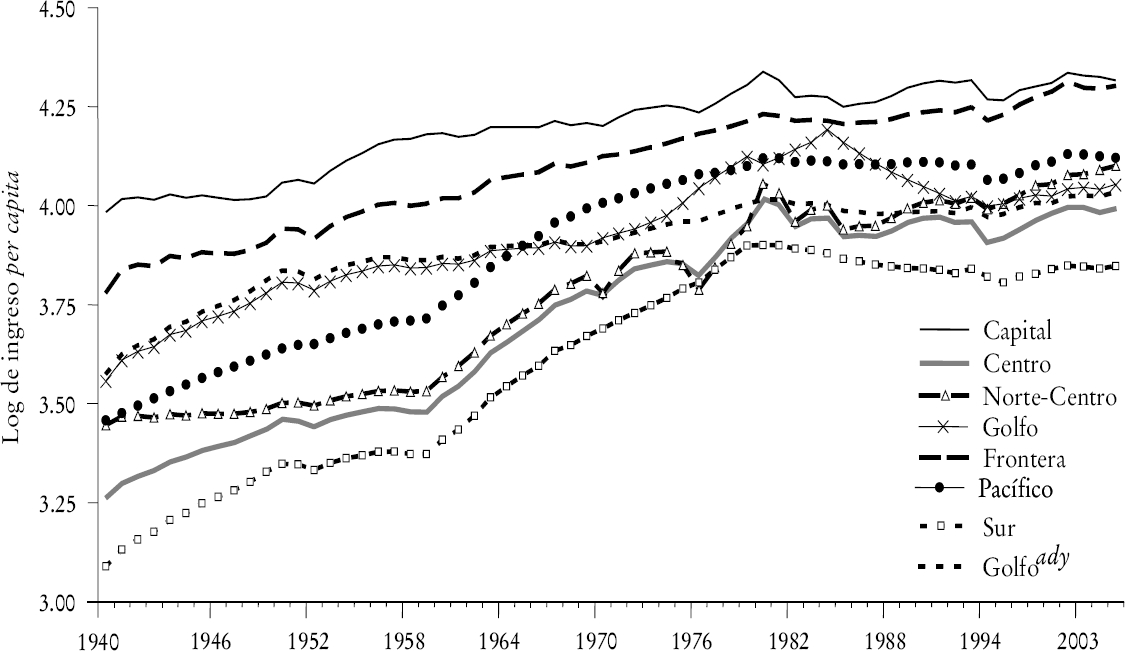
En la gráfica 6 se presenta la evolución del ingreso per capita para las siete regiones. Además, incluimos la región denominada Golfo ady (es decir, la región Golfo sin Campeche y Tabasco). En general, podemos afirmar que el ingreso per capita ha estado aumentan do en todas las regiones; sin embargo, el proceso de crecimiento no ha sido homogéneo. Por ejemplo, las regiones Centro, Norte-Centro, Pacífico y Sur tienen las mayores tasas de crecimiento del ingreso per capita de 1960 a 1980, y no obstante aún están muy rezagadas respecto a la Capital y Frontera. Además, el ingreso per capita del Pacífico era menor que el de las regiones Golfo y Golfo ady al inicio de la muestra, pero mayor en el año 2003. También está claro que la dispersión del ingreso es menor al final del periodo, lo que podría interpretarse como una reducción de la desigualdad entre las regiones ricas y las pobres.
En vista de la amplia variedad de patrones de comportamiento del ingreso per capita en relación con la región Capital, resulta difícil captar la dinámica del crecimiento durante los pasados 20 años viendo una gráfica. Por ejemplo, mientras que la disparidad entre la Capital y la región Frontera pare ce haber disminuido durante ese periodo, la brecha en el ingreso entre Capital y Sur parece estar aumentando desde 1985.
a) Prueba estándar de convergencia, ADF. Aplicamos primero la ADF tradicional para evaluar la existencia de raíz unitaria. El rechazo de la hipótesis nula (no estacionariedad) es evidencia de que impera el proceso de acercamiento sistemático (catching-up) o bien el de convergencia de largo plazo. Como se conoce, existen ciertas limitaciones asociadas con el empleo de esta metodología, lo que ha redundado en una es casa evidencia de convergencia. Entre esas limitaciones están: i) la poca potencia de la prueba y ii) como lo señalan Campbell y Perron (1991), el hecho de que la especificación del modelo sea errónea, o bien la existencia de cambios estructurales, sesga los resultados de la prueba hacia el no rechazo de la hipótesis nula; esto es en particular importante cuando se usan datos para un periodo extenso.
Al estimar la ecuación 2 usamos el criterio de información de Akaike (CIA) como una guía de selección para determinar el valor de n. Los resultados correspondientes se presentan en el cuadro 3. La hipótesis de raíz unitaria puede rechazarse a 5% para el Norte-Centro, Golfo ady y Frontera, y a 10% para la región Golfo. Por una parte, la estimación conjunta de α < 0 y β < 0 sugiere que las regiones Norte-Centro, Golfo y Frontera se han acercado sistemáticamente (catching-up) respecto a la región Capital durante todo el periodo. Por otra parte, la estimación de una tendencia estadísticamente no significativa y el rechazo de la hipótesis de raíz unitaria evidencian la convergencia de largo plazo entre las regiones Capital y del Golfo ady , lo que implica que la diferencia en el ingreso per capita no varía en el tiempo. Finalmente, la columna 5 muestra el número de rezagos usa do en la estimación, y la columna 6 presenta el estadístico Q, que indica que no hay suficiente evidencia para rechazar la hipótesis nula de residuos con propiedades de ruido blanco (white noise residuals).
Cuadro 3 Análisis de τ convergencia (1940-2003)
| Región | βa | αa,b | R 2 | k | Q(20)c | Conclusión | |
| 2 | Centro | −0.0014*** (−2.59) |
−0.0843 (−2.85) |
0.45 | 3 | 13.36 (0.86) |
Loose catching-up |
| 3 | Norte-Centro | −0.0033*** (−3.62) |
−0.2015** (−3.81) |
0.34 | 6 | 18.67 (0.54) |
Catching-up |
| 4 | Golfo | −0.0007* (−1.86) |
−0.1603* (−3.35) |
−0.37 | 6 | 28.58 (0.11) |
Catching-up |
| 4b | Golfo ady | 0.0001 (0.83) |
−0.1507** (−3.81) |
0.45 | 1 | 25.55 (0.18) |
Convergencia a largo plazo |
| 5 | Frontera | −0.0018*** (−4.19) |
−0.3180*** (−4.19) |
0.35 | 6 | 23.29 (0.27) |
Catching-up |
| 6 | Pacífico | −0.0009* (−1.68) |
−0.0773 (−2.20) |
0.36 | 6 | 13.42 (0.85) |
Loose catching-up |
| 7 | Sur | −0.0014** (−2.05) |
−0.0774 (−2.44) |
0.41 | 6 | 15.91 (0.72) |
Loose catching-up |
a El número entre paréntesis es el estadístico t; *, ** y *** denotan la significación estadística a 10, 5 y 1%, respectivamente.
b Los valores críticos se tomaron de Mackinnon (1991).
c Los p valores están entre paréntesis.
Encontramos evidencia considerable contra la hipótesis nula de no estacionariedad en cuatro de siete casos. Ésta es por en de favorable a la convergencia estocástica y determinista, en contraste con lo encontrado antes por estudios relacionados. No podemos rechazar la hipótesis de raíz unitaria para las regiones más pobres. Esto puede deberse a que las reformas comerciales tuvieron un importante efecto en su dinámica de crecimiento, aspecto del que hasta ahora hemos hecho caso omiso.
b) Prueba de convergencia,Nahar e Inder. Nahar e Inder (2002) propusieron dos definiciones de convergencia: i) relacionada con el ingreso per capita promedio de las economías que se analizan, y ii) relacionada con el ingreso per capita del líder del grupo. Los autores también propusieron una nueva prueba para examinar ambos casos. Para que exista convergencia respecto al ingreso promedio, las desviaciones cuadradas regionales en relación con el ingreso promedio deben siempre aproximarse a 0 con el transcurso del tiempo y la tasa de cambio respecto al tiempo debe ser negativa. Para que sea sostenible la convergencia respecto al líder del grupo, la brecha del ingreso entre el líder y cada una de las regiones debe siempre aproximarse a 0 y la tasa de cambio en relación con el tiempo debe ser positiva. En ambos casos, se ajusta un polinomio lineal a la brecha del ingreso.5
Esta pendiente promedio puede obtener se como sigue:6
en que
Para probar la convergencia respecto al ingreso medio definimos
Cuadro 4 Prueba de Nahar e Inder de convergencia
| Convergencia con la región capital | Convergencia a la media | |||||||||
| Región | k |
Pendiente promedio |
Estadístico t | p valor | k |
Pendiente promedio |
Estadístico t | p valor | ||
| 1 | Capital | 6 | −0.0175 | −14.65* | 0.00 | |||||
| 2 | Centro | 6 | 0.0174 | 15.36* | 0.00 | 6 | −0.0052 | −10.32* | 0.00 | |
| 3 | Norte-Centro | 6 | 0.0131 | 9.99* | 0.00 | 6 | 0.0002 | 0.31 | 0.38 | |
| 4 | Golfo | 6 | 0.0092 | 7.56* | 0.00 | 6 | 0.0005 | 2.38 | 0.01 | |
| 4 | Golfo ady | 5 | 0.0070 | 9.66* | 0.00 | 6 | −0.006 | 2.80 | 0.00 | |
| 5 | Frontera | 6 | 0.0078 | 13.29* | 0.00 | 5 | −0.035 | −8.29* | 0.00 | |
| 6 | Pacífico | 6 | 0.0147 | 13.35* | 0.00 | 6 | −0.0003 | −2.78* | 0.00 | |
| 7 | Sur | 6 | 0.0194 | 17.09* | 0.00 | 6 | −0.0126 | −18.61* | 0.00 | |
* Indica evidencia en favor de convergencia a 1% de significación.
Los resultados de la prueba de Nahar e Inder se presentan en el cuadro 4. Se muestra el polinomio estimado, la pendiente promedio, el valor del estadístico asociado con la hipótesis nula de no convergencia y los correspondientes p valores. Por una parte, los resultados indican una fuer te evidencia en favor de la hipótesis de convergencia respecto al líder del grupo: la región Capital. Además, las estimaciones sugieren que las regiones más pobres (Centro y Sur) están cerrando más rápidamente la brecha respecto a la región Capital —a tasas de más de 1.5% al año—. Por otra parte, los resultados muestran evidencia ambivalente en lo que respecta a la convergencia del ingreso per capita me dio. Las regiones Norte-Centro, Golfo y Golfo ady tienen pendientes promedio positivas, lo que evidencia la divergencia respecto al ingreso per capita medio. Para el resto de las regiones: Capital, Centro, Frontera, Pacífico y Sur, la prueba sugiere que la brecha del ingreso per capita no aumenta ni disminuye.
En vista de que hay una mayor variedad de resultados cuando se realiza el análisis de convergencia con la metodología ADF que con el procedimiento de Nahar e Inder, los resultados obtenidos anteriormente no son del todo comparables. La metodología ADF distingue entre los siguientes resultados: convergencia, divergencia, catching-up/lagging-behind, y loose catching-up/loose lagging-behind, mientras que la prueba de Nahar e Inder sólo diferencia entre convergencia y divergencia. No obstante, es posible establecer cierta semejanza entre sus resultados por que ambas encuentran evidencia contra divergencia.9
c) Prueba de convergencia, ADF con un cambio estructural de la tendencia. Perron (1989) mostró que la efectividad de las pruebas de raíces unitarias disminuye significativamente en presencia de rompimientos estructurales, pues sesga los resultados en favor del no rechazo de la hipótesis nula. Permitir un quiebre estructural en la función de la tendencia en el periodo pos terior a la reforma comercial corrige ese sesgo aumentan do la potencia de la prueba, mientras que a la vez ha ce posible describir el proceso de convergencia después de la liberación. La ruptura representa el efecto que pudo haber sufrido el ingreso per capita regional como consecuencia de una política económica específica y elimina su influencia de la “función de ruido” (noise function). Específicamente el modelo propuesto es,
en que DT t representa la variable de quiebre de la tendencia (dummy); DT t = t − T B si t > 1985 y 0 en cualquier otro caso, y T B = 1985 es la fecha del rompimiento estructural. Como se dijo líneas arriba, comparamos todas las regiones con la región 1, por tanto, j = 2, 3, ..., 7. Si la brecha del ingreso aumenta después de 1985, podemos esperar que nuestra estimación resulte en un valor σ mayor que 0. Se estimó la ecuación 4 por el método de mínimos cuadra dos ordinarios y, como anteriormente, usamos el CIA para seleccionar n.
Los resultados en el cuadro 5 muestran mayor evidencia contra la raíz unitaria; parece que la razón del no rechazo de la hipótesis nula en la sección anterior es el sesgo causado por la omisión del quiebre estructural. De manera similar a la estimación previa, encontramos evidencia que permite señalar que las regiones Norte-Centro, Golfo y Frontera se están acercando sistemáticamente a la región Capital; sin embargo, en este caso la hipótesis de raíz unitaria es rechaza da con un nivel de confianza más alto. Además, ahora hay evidencia de que las regiones Centro, Pacífico y Sur también tienen un proceso similar; pensamos que la nueva especificación nos permite rechazar la no estacionariedad para es tas regiones porque su patrón de crecimiento sufrió un cambio significativo después de las reformas comerciales. Esto implica que la no inclusión del cambio estructural tuvo un efecto importante en su función ruido. Lo anterior se observa en las estimaciones altamente significativas del parámetro θ; permitir un cambio estructural en el periodo de posliberación mejora significativamente el ajuste del modelo.
Cuadro 5 τ convergencia con rompimiento estructural en la tendencia determinista
| Región | βa | αa,b | θa | R 2 | k | Q(20)c | Conclusión | |
| 2 | Centro | −0.0035*** (−3.34) |
−0.1603** (−3.58) |
0.0030** (2.19) |
0.49 | 6 | 10.02 (0.95) |
1. Catching-up 2. Disminución del catching-up después de las reformas comerciales |
| 3 | Norte-Centro | −0.0036*** (3.22) |
−0.2059** (−3.78) |
0.0007 (0.41) |
0.35 | 6 | 18.89 (0.52) |
1. Catching-up 2. Ningún efecto significativo después de las reformas comercio exterior |
| 4 | Golfo | −0.0018*** (−2.63) |
−0.2175** (−3.90) |
0.0035* (1.87) |
0.41 | 6 | 28.72 (0.11) |
1. Catching-up 2. Disminución del catching-up después de las reformas comerciales |
| 4b | Golfo ady | 0.0003 (1.25) |
−0.1456** (−3.64) |
−0.0007 (−0.93) |
0.46 | 1 | 26.75 (0.11) |
1. Convergencia a largo plazo 2. Ningún efecto significativo después de las reformas comerciales |
| 5 | Frontera | −0.0017*** (−3.71) |
−0.3189*** (−4.16) |
−0.0002 (−0.27) |
0.36 | 6 | 16.44 (0.68) |
1. Catching-up 2. Ningún efecto significativo después de las reformas comerciales |
| 6 | Pacífico | −0.0038*** (−3.34) |
−0.1945** (−3.67) |
0.0049*** (2.82) |
0.45 | 6 | 12.58 (0.89) |
1. Catching-up 2. Disminución del catching-up después de las reformas comerciales |
| 7 | Sur | −0.0043*** (−3.42) |
−0.1726** (−3.73) |
0.0053*** (2.70) |
0.49 | 6 | 18.36 (0.56) |
1. Catching-up 2. Disminución del catching-up después de las reformas comerciales |
a El número entre paréntesis es el estadístico t. *, ** y *** denotan significación estadística a 10, 5 y 1%, respectivamente.
b Los valores críticos se tomaron de Mackinnon (1991).
c Los p valores se muestran entre paréntesis.
Las estimaciones muestran que las disparidades del ingreso per capita disminuyeron durante el periodo 1940-2003. No obstante, este proceso se interrumpió bruscamente después de 1985 en las regiones Centro, Golfo, Pacífico y Sur: se estima que la disparidad del ingreso, que disminuía antes del las reformas, quedó estable después de éstas.10 En estudios relacionados se argumenta que la región Frontera se benefició en particular de las reformas, pues incluye a todos los esta dos que comparten frontera con los Estados Unidos; los resultados no encuentran evidencia concluyen te en favor de esa afirmación: aunque nuestra estimación de θ es negativa para esta región, es estadísticamente no significativa.
Lo que sugieren nuestras estimaciones es evidencia de convergencia absoluta. La tasa a la que las regiones han estado “acortando distancia” respecto a la región Capital depende del ingreso inicial. El valor absoluto estimado del parámetro β es mayor para las regiones iniciales más pobres. Las regiones Golfo y Golfo ady merecen que se las estudie con más detalle. La riqueza petrolera de Campeche y Tabasco sesga nuestros resultados hacia la conclusión de que el ingreso per capita de la región Golfo está alcanzando al de la región 1. No obstante, cuando se excluye a esos dos estados, las estimaciones muestran que el ingreso per capita del resto de los estados en esa región —Quintana Roo, Vera cruz y Yucatán— no ha cambiado en relación con el de la región Capital. Esto implica que los resultados cualitativos respecto al efecto de Campeche y Tabasco no han cambiado respecto a los de la sección I.
III. Convergencia entre regiones fronterizas de México y los Estados Unidos
Los estudios empíricos que buscan determinar si la liberación comercial contribuye a la convergencia del ingreso per capita entre países han producido resultados mixtos. Por una parte, Slaughter (2001) evalúa cuatro ejemplos de importantes liberaciones comerciales multilaterales y no encuentra evidencia para afirmar que hayan contribuido a la convergencia del ingreso. En realidad, el comercio parece haber causado divergencia en los ingresos. Sin embargo, Ben-David (1993, 1994 y 1996) encuentra que la eliminación de las barreras comerciales lleva a una disminución notoria de la brecha de ingresos.
La reforma comercial en México es un episodio que parece constituir un laboratorio natural para analizar el efecto de la liberación económica en la diferencia de los ingresos per capita. Puesto que los resultados anteriores sugieren que la región fronteriza mexicana se ha beneficia do particularmente de la liberación económica, nos centramos en la investigación de las propiedades de la brecha del ingreso de las regiones fronterizas de México y los Estados Unidos.
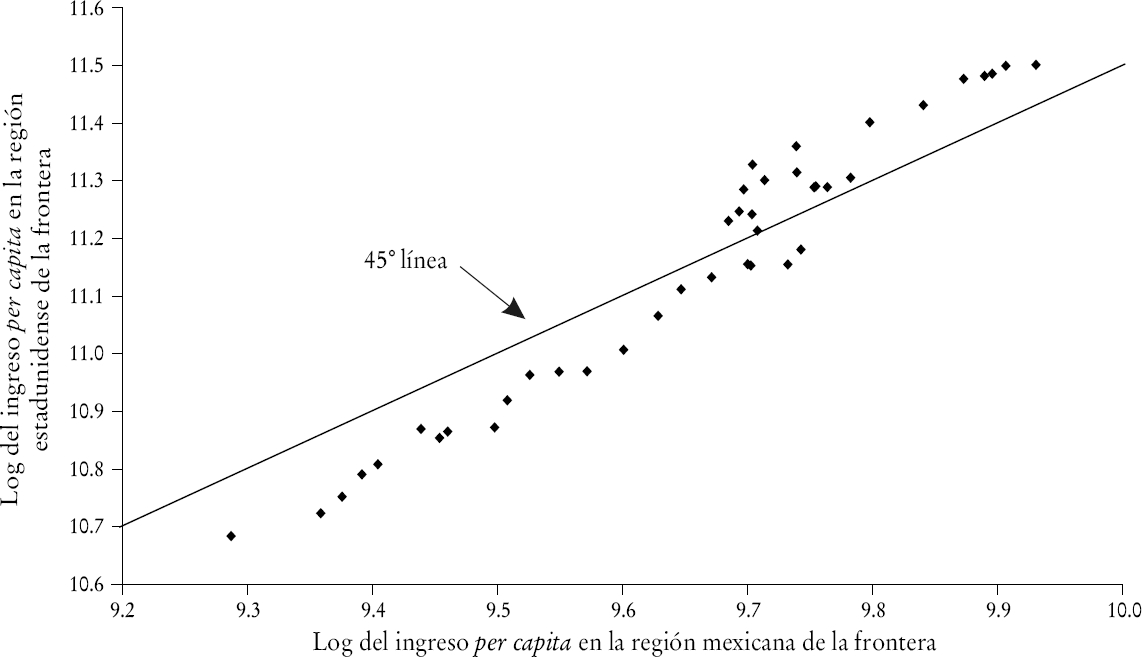
Para realizar este análisis usamos datos11 para los estados que comparten frontera con México. Después, calculamos el producto regional bruto (PRB) ajustado por PPC para cada región de ambos lados de la frontera. El diagrama de dispersión de la gráfica 7 sugiere que la región de los Estados Unidos creció más rápidamente que la mexicana, dado que la línea de la gráfica de dispersión tiene una pendiente mayor a 45°. Esta pauta de rezago no cambió después de 1985. Así, las reformas aparentemente no cambiaron la dinámica del ingreso per capita que se había observado desde 1963. Para hacer formalmente pruebas de convergencia realizamos el mismo análisis que en las subsecciones a y c de la sección II.2. Los resultados se presenta en el cuadro 6.
Cuadro 6 Análisis de τ convergencia para las regiones fronterizas de México y los Estados Unidos
| Modelo | βa | αa,b | θa | R 2 | k | Q(20)c |
| (2) | 0.0030*** (2.96) |
−0.4672* (−3.29) |
0.24 | 1 | 13.77 (0.84) |
|
| (4) | 0.0030** (2.56) |
−0.4645* (−3.18) |
−0.0001 (−0.11) |
0.24 | 1 | 13.76 (0.84) |
a El número entre paréntesis es el estadístico t. *, ** y *** denotan significación estadística a 10, 5 y 1%, respectivamente.
b Los valores críticos se tomaron de Mackinnon (1991).
c Los p valores están entre paréntesis.
Se rechaza la hipótesis nula de divergencia y el parámetro de la tendencia determinista es positivo y estadísticamente significativo en ambos modelos. Lo anterior implica que las disparidades en el ingreso per capita están aumentando durante todo el periodo; esto nos lleva a la conclusión de que la región fronteriza mexicana está rezagándose respecto a su contraparte estadunidense. De acuerdo con los resultados, no existe evidencia estadística para afirmar que las reformas comerciales iniciadas a mediados de los años ochenta modificaron la tasa a la cual se amplía la brecha del ingreso —sin embargo, el parámetro estimado del rompimiento estructural de la tendencia, θ, es negativo, aunque no significativo estadísticamente en el modelo (4).
Conclusiones
Realizamos un análisis de τ convergencia para las regiones mexicanas durante el periodo 1940-2003; los resultados sugieren que las disparidades en el ingreso estaban disminuyendo en relación con el ingreso de la región Capital. Hay evidencia en favor de convergencia absoluta, pues las tasas a las que las regiones pobres reducen las diferencias en el ingreso dependen de su riqueza inicial. Al contrario de estudios relacionados que analizan la hipótesis de convergencia con series en el tiempo, encontramos fuer te evidencia contra la hipótesis nula de raíz unitaria; dicha evidencia es aún más fuer te cuando se incluye una ruptura estructural en la tendencia determinista para modelar cualquier efecto que las reformas comerciales puedan haber tenido. Podemos describir las características específicas del patrón de crecimiento para cada región, tanto antes como después de la liberación económica.
Nuestros resultados son congruentes con la hipótesis de que las reformas comerciales afectaron negativamente algunas áreas de México. Lo que aquí mostramos es evidencia que apoya la afirmación de que ha ocurrido un aumento en la brecha del ingreso entre la región Capital y las regiones Centro, Pacífico y Sur, y determinamos cuantitativa y cualitativamente la significancia relativa de ajuste en el patrón de crecimiento regional después de este acontecimiento. Estos hallazgos concuerdan con los de Chiquiar (2005), quien argumenta que, después de 1985, “sólo los estados relativamente ricos tuvieron las características adecuadas para aprovechar las ventajas de las nuevas fuentes de crecimiento provenientes de las mejores oportunidades para comerciar”. Por una parte, los estados fronterizos estaban dotados de mejor infraestructura en comunicaciones y transportes, mayor capital humano y físico y están ubicados jun to al mayor mercado del mundo. Éstos pudieron, por tanto, aprovechar la mayoría de los beneficios que el comercio exterior podía ofrecer. Por otra parte, los estados que pertenecen a las regiones Centro, Pacífico y Sur no compartían esas características y, en consecuencia, no pudieron obtener los mismos beneficios.
Los resultados sugieren además que no hay ninguna evidencia estadística que permita afirmar que las reformas comerciales han modificado la tendencia observada previamente en el ingreso per capita entre las regiones fronterizas de México y de los Estados Unidos. Aunque esta región mexicana se ha beneficiado en particular con la liberación comercial, los beneficios no han sido suficientes para reducir de manera importante la brecha.











 nueva página del texto (beta)
nueva página del texto (beta)