1. El modelo estructural multivariado

Adoptamos como marco de análisis el modelo de series de tiempo estructural multivariado lineal gaussiano (^{Harvey, 1989}; ^{Harvey y Koopman, 1997}; ^{Durbin y Koopman, 2001}; ^{Carvalho y Harvey, 2005}). La presentación que sigue, incluida la notación, es la utilizada por los mencionados autores. Sea yt=(y1t,...,yNt) 'el vector del logaritmo del empleo ajustado por estacionalidad en las N regiones en el mes t, con t=1,...,T . Las series de empleo se pueden luego expresar directamente en término de sus componentes no observables, como la tendencia μt=(μ1t,...,μNt) ', el ciclo ψt=(ψ1t,...,ψNt) ' y el componente irregular εt=(ε1t,...,εNt) ', de manera que yt=μt+ψt+εt, εt~N0,Σt,t=1,..., T , en que Σε es la matriz N x N de varianza-covarianza de los componentes irregulares de las series de empleo.⁵

La tendencia está compuesta por dos trayectorias aleatorias; una para el nivel μt+1=μt+βt+ηt,ηt~N(0,Ση) , y otra para la pendiente βt+1=βt+ζt,ζt~N(0,Σζ) , para t=1,...,T y en la que Ση y Σζ son las matrices N × N de varianza-covarianza de las perturbaciones del nivel y de la pendiente de la tendencia, respectivamente.

Los ciclos regionales se asumen como similares (^{Harvey y Koopman, 1997}) y están generados por los procesos

en los que ψt y ψt* son vectores N×1 del componente cíclico regional y κt y κt* denotan vectores N×1 de las perturbaciones, de manera que Eκtκt'=Eκt*κt*'=Σκ,Eκtκt*'=0 en que Σκ es la matriz NxN de varianza-covarianzas de las perturbaciones cíclicas. Los ciclos son similares en el sentido de que el factor de convergencia o parámetro de persistencia ρ(conρ<1) y la duración del ciclo 2π/λ son los mismos en todas las regiones.

El grado de comovimiento cíclico entre las series de empleo regional se determina a partir de la correlación cruzada entre las perturbaciones de los ciclos regionales, mientras que la condición necesaria para la presencia de ciclos comunes es que la matriz de varianza-covarianza de las perturbaciones tenga rango menor a N (^{Carvalho y Harvey, 2005}; ^{Koopman y Lucas, 2005}; ^{Commandeur y Koopman, 2007}).

Si se considera cada ciclo regional por separado se puede comprobar que esta especificación trigonométrica con dos variables del componente cíclico es simplemente la versión estocástica de la función circular ψt=αcosλt+βsinλt , con ψ0=α y ψ0*=β , para t = 1,... ,T. Si bien es posible agregar un componente irregular a la función circular y así generar fluctuaciones, la amplitud y la fase de los ciclos resultantes, que vienen determinadas por los parámetros α y β , se mantendrían constantes. En cambio, la versión trigonométrica con dos variables permite obtener ciclos con amplitud y fase variables. Además, esta especificación permite la inclusión de un parámetro de persistencia para que tanto la estimación como los pronósticos del componente cíclico sean estables y convergentes (^{Harvey y Koopman, 1997}).

El supuesto de ciclos similares facilita (en el contexto de un modelo de series de tiempo multivariado estimado por el método de espacio de estados) la descomposición de las series y la identificación del ciclo. Lo anterior debido a que se reduce de manera significativa el número de parámetros por estimar y se agiliza la convergencia del algoritmo numérico iterativo utilizado en la estimación (véase la subsección 3 líneas abajo).

El supuesto de ciclos similares constituye, por otra parte, una limitación, ya que para efectos de la identificación de las fluctuaciones del empleo en las frecuencias del ciclo económico se impone una duración del ciclo igual para todas las regiones. Una consecuencia de lo anterior es que, en algunas regiones, podrían existir fluctuaciones cíclicas del empleo en frecuencias más altas o más bajas que no se considerarán parte del ciclo económico. Sin embargo STAMP, el programa utilizado para la estimación del modelo, mitiga el efecto del supuesto al permitir también el filtrado y el análisis de estas fluctuaciones cíclicas de alta y baja frecuencia. El resultado de ello es que en algunas ocasiones la especificación con el mejor ajuste contendrá dos ciclos: uno de ellos, el de mayor interés, representará las fluctuaciones en las frecuencias del ciclo económico, mientras que el otro estará captando fluctuaciones de menor duración asociadas con otros fenómenos.⁶

Otra limitación, tal vez más relevante, del supuesto de ciclos similares es que elimina cualquier causalidad entre los ciclos regionales; ésta se analiza con más detalle líneas abajo en la subsección III.3.

2. Análisis de la varianza

Para estudiar el comovimiento entre empleo regional y nacional recurrimos al análisis de componentes principales (ACP) de las perturbaciones del ciclo. El ACP consiste en la diagonalización EDE' de la matriz de varianza-covarianzas de las perturbaciones del ciclo Σκ , en que E es la matriz característica y D la matriz diagonal con los valores característicos. Los componentes principales de las perturbaciones estimadas son, simplemente, los vectores característicos de las referidas matrices de covarianzas, mientras que el valor característico asociado indica la varianza de las perturbaciones explicada por cada uno de ellos (^{Shlens, 2009}). Sea eij el elemento de la matriz característica asociado con la región i y el componente principal j, y sea dj el valor característico asociado con dicho componente principal; con N componentes principales tenemos que σi2=ΣjNeij2dj es la varianza del ciclo en la región i, por lo que la proporción de la varianza explicada por el componente principal j es eij2dj/σi2 (^{Carvalho y Harvey, 2005}). Cuanto mayor sea la proporción de la varianza de las perturbaciones explicada por el primer componente principal, mayor será el comovimiento del empleo regional con el nacional.

3. Estimación

La estimación del modelo estructural se realizó en STAMP 8 (^{Koopman et al, 2006}), que es un módulo del programa computacional OxMetrics 5. STAMP utiliza el filtro de Kalman para la obtención de los valores filtrados y suavizados del vector de estados (los componentes no observados de las series) y a partir de ellos (de manera iterativa y mediante un proceso de optimación numérica) estima por máxima verosimilitud las varianzas y covarianzas de las perturbaciones de los mencionados componentes (^{Durbin y Koopman, 2001}). En todos los casos los parámetros del modelo se obtuvieron usando el método BFGS de optimación numérica. STAMP instrumenta asimismo la descomposición de la matriz de varianza-covarianza de las perturbaciones para obtener la matriz característica y el vector de valores característicos (^{Koopman et al, 2006}).

En el método de espacio de estados la estimación de los componentes de las series se realiza de maneta directa y simultánea; es decir, no es necesario primero filtrar la tendencia para luego estimar un modelo para el componente cíclico estacionario, como en el método de Box-Jenkins. También es importante señalar que los modelos estructurales tienen una representación equivalente en términos de los modelos ARIMA, y que por tanto son más generales que éstos últimos (véase en ^{Durbin y Koopman, 2001}, y ^{Commandeur y Koopman, 2007}, un análisis más completo).

4. Elección entre modelos

Usando STAMP estimamos tres modelos del logaritmo de la serie desestacionalizada del empleo formal permanente; en dos de ellos la tendencia es estocástica y en uno es determinística. En el modelo 1 suponemos que la tendencia sigue una trayectoria aleatoria con deriva (random walk with drift); ello implica imponer ζt=0, t=1,...,T, en el modelo de la sección anterior, por lo que la tendencia viene dada por la expresión μt+1=μt+β+ηt,ηt~N(0,Ση) , es decir, la pendiente de la tendencia se mantiene constante, mientras que el nivel es estocástico. En el modelo 2, suponemos que el empleo sigue una tendencia suave (smooth trend o integrated random walk); ello implica imponer ηt=0, t=1,..., T en el modelo, por lo que el nivel se mantiene constante y la pendiente es βt-1=βt+ζt,ζt~N(0,Σζ) . Finalmente, en el modelo 3 la tendencia es determinística; en este caso imponemos ζt=0 y ηt=0, t=1,..., T .

Siguiendo a ^{Koopman y Lucas (2005)}, y por las razones mencionadas al final de la subsección 1, estimamos dos versiones de cada modelo: la versión "a", con un ciclo trigonométrico de duración no mayor de cinco años, y la versión "b" con dos ciclos trigonométricos, uno corto con duración menor de cinco años, y otro largo con duración de entre cinco y 10 años.

Por último, el mejor modelo del empleo regional debe cumplir con dos condiciones: i) los errores de pronóstico a un periodo estandarizados (standardized one-step-ahead forecast error) deben tener una distribución normal, ser homoscedásticos e independientes (no están autocorrelacionados), y ii) el valor del criterio de información de Akaike (CIA) es el menor de todos los modelos considerados (^{Commandeur y Koopman, 2007}).

a) Pruebas de diagnóstico. El error de pronóstico a un periodo estandarizado se define como et=νt/Ft , en el que νt es el error de pronóstico y Ft su varianza; ambos estadísticos se obtienen durante la aplicación del filtro de Kalman para la estimación de los componentes no observables del modelo. En STAMP la hipótesis nula de normalidad de los errores se rechaza cuando el estadístico N de Bowman-Shenton, calculado a partir del coeficiente de simetría y de la curtosis, excede el valor crítico a 5% de confianza de la distribución χ2 con dos grados de libertad (5.99).

La prueba de homoscedasticidad de los errores se basa en el estadístico H(h), el cociente de la varianza de los últimos h errores y la varianza de los primeros h errores; normalmente STAMP establece un valor de h cercano a T/3 (en nuestro caso h = 48). Un valor alto de H(h) indica que la varianza aumenta con el tiempo, por lo que la hipótesis nula de homoscedasticidad se rechaza si el estadístico es mayor que el valor crítico al 5 % de la distribución F, F(h, h; 0.025), dado que es una prueba a dos colas -en nuestro caso F(48, 48; 0.025) = 1.615-. Si H(h) > 1, basta comparar ambos valores; si H(h) < 1, entonces la hipótesis nula se rechaza si Hh-1>F(h,h;0.025) .

En STAMP la prueba de independencia de los errores consiste en verificar que el grado de autocorrelación en el primer rezago, r(1), y en rezago T/6 [en nuestro caso r(24)] no sea distinto de 0; es decir, no debe exceder el intervalo de confianza de 95% dado por los límites ±2/T (con 148 observaciones, el valor crítico es ±0.1644 ). STAMP también calcula el estadístico Box-Ljung, Q(p, q), basado en las primeras p autocorrelaciones, que debe ser comparado con el valor de 5% de la distribución χ2 con q grados de libertad; en nuestro caso, STAMP arroja los valores para Q(24, 24 - d), en que d es el número de parámetros por estimar en el modelo. En la versión "a" del modelo d = 5, mientras que en la versión "b", con dos ciclos, d = 6, por lo que los valores críticos son Q(24, 19) = 30.14 y Q(24, 18) = 28.87, respectivamente. Además, se presenta el conocido estadístico de Durbin-Watson (DW). Un análisis técnico más pormenorizado de todas las pruebas mencionadas en esta sección se puede encontrar en ^{Harvey (1989)}, ^{Commandeur y Koopman (2007)} y ^{Koopman et al (2006)}.

b) Elección del mejor modelo. Los supuestos de normalidad y homoscedasticidad son rechazados en la mayoría o en todos los modelos de las regiones CT, VM, ON, SR y SE. La homoscedasticidad es rechazada en la mayoría de los modelos de CO. En las regiones NO, NT, NE y OT el supuesto de homoscedasticidad no es rechazado en la mayoría de los modelos. En esas regiones, el supuesto de normalidad nunca es rechazado en el modelo 2b (Cuadro 2).⁷

FUENTE: Elaboración propia con datos desestacionalizados de la STPS.

^a Los modelos están numerados según la especificación de la tendencia del empleo; ésta puede estar caracterizada por una trayectoria aleatoria con deriva (modelo 1), una trayectoria aleatoria suave (modelo 2) o por una trayectoria determinística (modelo 3). En estos modelos se supone la existencia de 1 ciclo (caso "a") o de dos ciclos, uno corto y uno largo (caso "b").

* Indica rechazo de la hipótesis nula correspondiente. Para r(1) y r(24) el valor crítico es +(-) 0.1644; para Q(24) los valores críticos son 30.14 (modelos "a") y 28.87 (modelos "b"); el valor crítico para la prueba de normalidad es 5.99; por último, el valor crítico para H(48) es 1.615 (las pruebas de diagnóstico se analizan de manera pormenorizada en la subsección II.4.a).

Cuadro 2 Pruebas de diagnóstico de seis modelos estructurales del empleo regional^a 

Del supuesto de independencia (el más importante de los tres supuestos de los errores), podemos decir lo siguiente. El estadístico DW es más cercano al valor de 2 en los modelos 2a, 2b y 1b, pero sobre todo en el modelo 2a. Se sitúa muy por debajo del valor de 2 en el resto de los modelos. Asimismo, los errores no están autocorrelacionados a un rezago en los modelos 1b, 2a y 2b en todas las regiones con excepción de NT, y en general si lo están en el resto de los modelos en todas las regiones. En ocho de 10 regiones, los errores tampoco están autocorrelacionados en el rezago 24 en los modelos 2a y 2b, y en nueve de 10 regiones tampoco lo están en el modelo 1b. Por otra parte, se rechaza la presencia de autocorrelación en los errores para los primeros 24 rezagos en el modelo 2b (en ocho de 10 regiones), en el modelo 2a (siete de 10 regiones) y en el modelo 1b (en seis de 10 regiones). Respecto al CIA, los modelos 1b, 2a y 2b son los que presentaron los valores más bajos (Cuadro 2).

En resumen, consideramos que los modelos 1b, 2a y 2b son los que mejor pasan las pruebas de diagnóstico, mientras que los modelos 1a, 3a y 3b en general no satisficieron los criterios establecidos (Cuadro 2). Sin embargo, los modelos 2a y 2b no parecen producir una representación satisfactoria de los ciclos del empleo en México. En particular, la duración de los ciclos estimados es muy corta, 2.3 años para el ciclo largo y 0.7 años para el ciclo corto. Según INEGI (s/f), la duración promedio de los ciclos económicos del tipo clásico en México desde 1980 es de 62 meses, un poco más de cinco años. Ello nos deja entonces con el modelo 1b, en el que la tendencia se modela como una trayectoria aleatoria con deriva, y en el que el ciclo largo tiene una duración similar al ciclo de la economía mexicana (6.3 años).

5. Otros métodos

Existe una extensa bibliografía acerca de métodos paramétricos para el estudio del comovimiento de las series de tiempo. La base de la misma son los desarrollos de ^{Engle y Granger (1987)} y ^{Stock y Watson (1988)}, que buscaron modelar el comovimiento de largo plazo de las series macroeconómicas a partir de la noción de cointegración y de la estimación de tendencias comunes, y de ^{Engle y Kozicki (1993)}, que estudiaron el comovimiento cíclico a partir de las noción de "propiedades comunes" (common features). Posteriormente ^{Vahid y Engle (1993)} integraron ambas vertientes con el objetivo de probar la existencia de ciclos comunes en series de tiempo cointegradas. Estos últimos autores sostienen que la presencia de tendencias comunes, es decir de comovimiento de largo plazo, es una restricción que debe ser considerada a la hora de probar la existencia de ciclos comunes en un conjunto de series de tiempo. La metodología fue utilizada, por ejemplo, por ^{Herrera Hernández (2004)} para probar la existencia de un ciclo común entre las economías de México y los Estados Unidos.

Los métodos paramétricos han sido criticados recientemente por presentar algunas debilidades; entre otras, se señaló que la cointegración, los ciclos comunes o las propiedades comunes no implican, ni tampoco son implicados, por la presencia de una correlación alta entre las series del empleo; también se señaló la inconveniencia de que estos métodos no pueden ser utilizados para medir el grado de comovimiento y por tanto realizar comparaciones entre economías distintas (^{Croux, Forni y Reichlin, 2001}, y ^{Carlino y DeFina, 2004}). Por ello autores como ^{Rissman (1999)}, ^{Kouparitsas (2002)} y ^{Norman y Walker (2004)} han utilizado métodos no paramétricos, en particular el método de componentes no observados, para estimar un ciclo común en las series de empleo regional. Además, en este caso, el método permite medir el grado de comovimiento entre una región y las demás como la variabilidad de la tasa de crecimiento del empleo explicada por el ciclo común.

^{Carvalho y Harvey (2005)} proponen un tercer método, que aplicamos en este trabajo, en el que la medición del comovimiento regional se realiza independientemente de la existencia de un ciclo común, como se analiza la subsección 1. Existen, asimismo, otros dos métodos que no requieren la determinación previa de un ciclo común para determinar el grado de comovimiento; por una parte, ^{Christiano y Fitzgerald (1998)} estiman el comovimiento utilizando el método de la coherencia cuadrática (esto es, el R2 de la regresión del componente cíclico del empleo de un sector o región en el componente cíclico del empleo total); por otro, ^{Croux, Forni y Reichlin (2001)} y ^{Carlino y DeFina (2004)} estiman el comovimiento con un índice de cohesión, que mide la correlación dinámica entre los componentes cíclicos de las series de empleo.

Las ventajas y desventajas de la metodología propuestas por ^{Vahid y Engle (1993)} respecto a la propuesta por ^{Harvey y Koopman (1997)} y ^{Carvalho y Harvey (2005)} son las siguientes: por una parte, la ventaja de la metodología seguida en este documento es que permite estimar el componente cíclico de las series para distintas especificaciones de la tendencia estocástica y luego elegir el mejor modelo con base en el análisis de las propiedades estocásticas del componente irregular (el error de estimación) y en el grado de ajuste a la economía nacional de los ciclos estimados. La desventaja del método consiste en la imposición de la condición de "similares" a los ciclos, lo que puede limitar su estudio posterior (por ejemplo, la causalidad entre ellos; veáse el análisis en la subsección III.3).

Por otra parte, el método propuesto por ^{Vahid y Engle (1993)} arroja tendencias que se parecen mucho a la tendencia suave (integrated randam walk) y, consecuentemente, ciclos de menor duración que se alejan de la representación que por lo común se tiene de los ciclos económicos. La ventaja del método de ^{Vahid y Engel (1993)} reside en que el número de tendencias y de ciclos comunes guardan una relación de congruencia estadística entre ellos y que se pueden determinar a partir de pruebas de hipótesis, mientras que en el modelo no paramétrico el número de tendencias y de ciclos comunes se determinan independientemente uno del otro. Mientras en ^{Vahid y Engle (1993)} la descomposición de las series en tendencia y ciclo es en gran parte una consecuencia del número de tendencias y ciclos comunes presente en las mismas, en ^{Harvey y Koopman (1997)} el número de componentes comunes es consecuencia de la descomposición obtenida. Por último, la definición de comovimiento es menos estricta en ^{Harvey y Koopman (1997)} que en ^{Vahid y Engel (1993)}; mientras que los segundos consideran que existe comovimiento sólo si hay tendencias o ciclos comunes, los primeros consideran la posibilidad de la existencia de comovimiento que no tiene su origen en tendencias o ciclos comunes.

1. Ciclo corto del empleo regional

El ciclo corto tiene una frecuencia de 2.05 años y una alta persistencia (el coeficiente del primer rezago del componente cíclico es 0.98). Por definición, estos resultados aplican al ciclo corto en todas las regiones. En términos de la volatilidad del ciclo, ésta es mayor en las tres regiones del norte, en ON y en CT que en el resto de las regiones. Las perturbaciones cíclicas del empleo de la región NO tienen la mayor varianza; ésta es 21 veces mayor que la varianza de las correspondientes a la región VM (Cuadro 3; se muestran los valores estimados multiplicados por 106 para facilitar su análisis). La correlación entre las perturbaciones cíclicas del empleo de las distintas regiones es mayor a 0.9 sólo entre NO y CT y entre NT y NE. En VM las innovaciones en el componente cíclico del empleo presentan una correlación baja con las del resto de las regiones, mientras que las perturbaciones cíclicas del SR están en la mayoría de los casos correlacionadas negativamente con las del resto de las regiones (Cuadro 4). Podemos concluir que respecto al ciclo corto del empleo regional, el comovimiento es bajo. A pesar de ello, los ciclos cortos regionales presentan una gran coincidencia temporal entre ellos (Gráfica 3). Sin embargo, los puntos de giro de este ciclo corto no parecen coincidir con las fechas del ciclo económico de la economía mexicana, excepto para el periodo recesivo de 2008 y 2009.

FUENTE: Elaboración propia con datos desestacionalizados de la STPS.

Cuadro 3 Ciclo corto del empleo regional 

FUENTE: Elaboración propia con datos desestacionalizados de la STPS.

Cuadro 4 Ciclo corto del empleo regional 

FUENTE: Elaboración propia con datos desestacionalizados de la STPS.

Gráfica 3 Ciclo corto del empleo regional 

El análisis de componentes principales señala la existencia de tres componentes principales importantes, que explican 62.0, 27.6 y 7.2% de la varianza total de las perturbaciones cíclicas. Los pesos tienen signos contrarios y varían en tamaño, con excepción de los pesos de la mayoría de las regiones en el primer componente principal (Cuadro 5). La relativamente baja proporción de la variabilidad total de las perturbaciones cíclicas que es explicada por el primer componente principal indica que estas fluctuaciones de alta frecuencia podrían deberse a factores de tipo específicamente regional, que en ocasiones coinciden con el ciclo de la economía mexicana y en otras no. Pero como veremos esto es más cierto para unas regiones que para otras.

FUENTE: Elaboración propia con datos desestacionalizados de la STPS.

Cuadro 5 Ciclo corto del empleo regional 

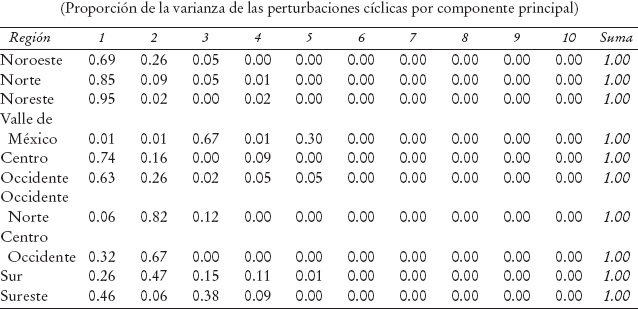
Para determinar la relación entre los ciclos cortos del empleo regional y el correspondiente ciclo corto del empleo nacional, calculamos la proporción de la varianza de las perturbaciones cíclicas del empleo en cada región asociadas a los distintos componentes principales. Encontramos que en el NE, NT y CT el 95, 85 y 74% de la varianza de las perturbaciones cíclicas están asociadas con el primer componente principal. La cifra es 69% para NO y 63% para OT; para el resto de las regiones la proporción es menor a 50, siendo la correspondiente a VM y ON 0 o cercana a 0 (Cuadro 6). En esta última región la variabilidad de las perturbaciones cíclicas está mayormente asociada al segundo componente principal. En SE y VM, el 38 y 67%, respectivamente, de la varianza de las perturbaciones cíclicas están asociadas con el tercer componente principal.

FUENTE: Elaboración propia con datos desestacionalizados de la STPS.

Cuadro 6 Ciclo corto del empleo regional 

Utilizando los pesos de cada región en cada uno de los componentes principales construimos los ciclos de corto plazo asociados a cada componente principal. El ciclo asociado al primer componente principal tiene un parecido muy cercano al del ciclo corto nacional (Gráfica 4a); Los ciclos asociados al segundo y tercer componente principal presentan comportamientos menos coherentes con los del empleo nacional (Gráfica 4b y ^c).

FUENTE: Elaboración propia con datos desestacionalizados de la STPS.

Gráfica 4 Ciclo corto del empleo nacional: observado versus inferido del empleo regional 

En resumen, en las regiones NO, NT, NE, OT y CT el ciclo corto parece estar asociado a igual ciclo corto del empleo nacional; en el resto de las regiones este ciclo corto parece ser más el resultado de choques regionales específicos.

2. Ciclo largo del empleo regional

El segundo ciclo, estimado a partir de las fluctuaciones del empleo en las frecuencias medias normalmente asociadas con el ciclo económico, tiene una duración de 6.27 años en todas las regiones y es asimismo muy persistente (el coeficiente del primer rezago es 0.99). A pesar de que se descarta la existencia de un ciclo común (la matriz de varianza-covarianzas de las perturbaciones cíclicas tiene rango completo), hay pruebas muy claras de alto comovimiento, tal vez asociado a la propagación interregional de choques regionales específicos.

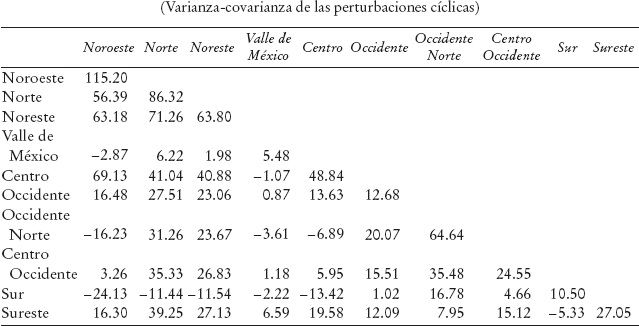
El grado de coincidencia de estos ciclos es muy alto, particularmente en los picos del ciclo, y las fluctuaciones que presentan coinciden con las fechas de las fases cíclicas de la economía mexicana (Gráfica 5). Las diferencias entre las regiones en términos de volatilidad del componente cíclico vuelven a aparecer en este caso. La varianza de las perturbaciones cíclicas es mayor en el NO y en el NE; ésta toma valores intermedios en NT, VM, CT, ON y SE, y bajos en OT, CO y sobre todo en el SR (Cuadro 7; se muestra los valores estimados multiplicados por 106 para facilitar su análisis).

FUENTE: Elaboración propia con datos desestacionalizados de la STPS.

Gráfica 5 Ciclo largo del empleo regional 

FUENTE: Elaboración propia con datos desestacionalizados de la STPS.

Cuadro 7 Ciclo largo del empleo regional 

El grado de comovimiento cíclico regional es alto; las correlaciones entre las innovaciones cíclicas en las distintas regiones son en general positivas y altas (Cuadro 8). Las regiones NO, NE y VM presentan altos niveles de correlación cíclica del empleo entre ellas. Las innovaciones cíclicas del empleo en OT están altamente correlacionadas con las del NO y NT; en el caso del SE, ello sucede con las tres regiones del norte. Las perturbaciones cíclicas del empleo de la región CT tienen una correlación alta con el NT, intermedia con OT y baja con el resto de las regiones -sobre todo con VM, ON y SR-. En el caso de la región OT, las correlaciones con las demás regiones toman valores altos e intermedios, con excepción del ON y el SR, en que son más bajas. Es notoria la diferencia entre las innovaciones cíclicas del empleo en el SE, que presentan un comovimiento alto con las de la mayoría de las regiones, y las del SR, cuyo comovimiento es intermedio o bajo (Cuadro 8).

FUENTE: Elaboración propia con datos desestacionalizados de la STPS.

Cuadro 8 Ciclo largo del empleo regional 

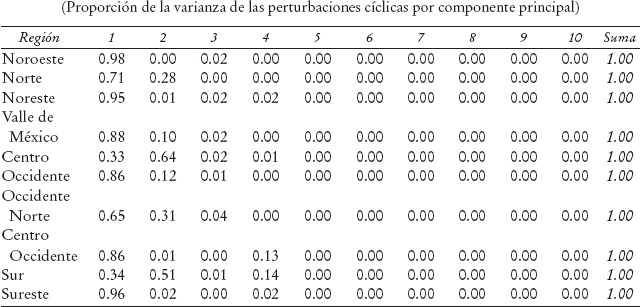
El análisis por componentes principales muestra que el ciclo asociado al primer componente principal explica 82.3% de la varianza de las perturbaciones cíclicas; mientras que el segundo componente principal explica 14.9% (Cuadro 9). La proporción de la varianza de las perturbaciones cíclicas explicada por el primer componente principal es mayor a 95% en NO, NE y SE; tiene valores altos e intermedios en VM (88%), OT (0.86), CO (0.86) y NT (0.71) y bajos en ON, SR y CT con 65, 34 y 33%, respectivamente (Cuadro 10). Un resultado inesperado es que la varianza de las perturbaciones cíclicas del empleo de la región CT esté mayormente asociada con el segundo componente principal, al igual que en el SR.

FUENTE: Elaboración propia con datos desestacionalizados de la STPS.

Cuadro 9 Ciclo largo del empleo regional 

FUENTE: Elaboración propia con datos desestacionalizados de la STPS.

Cuadro 10 Ciclo largo del empleo regional 

Usando los pesos de cada región en el primer componente principal (19.3, 13.7, 12.0, 11.3, 10.7, 10.1, 8.5, 6.3, 5.3 y 2.7% para las regiones NO, NE, VM, SE, ON, NT, OT, CT, CO y SR, respectivamente) estimamos el ciclo largo de empleo asociado con este componente principal. Encontramos que el ciclo así definido copia muy de cerca los movimientos cíclicos del empleo nacional (Gráfica 6). Estos resultados indican que el ciclo largo del empleo regional tiene como origen los mismos choques que perturban al empleo nacional, con excepción de los ciclos en CT y SR en los que mayormente se deben a choques de carácter regional específico. Antes señalamos que no se encontraron pruebas de un ciclo largo común, por lo que el alto grado de comovimiento cíclico en la mayoría de las regiones podría deberse a la propagación interregional de choques específicos (la razón por la que no es posible estimar explícitamente un modelo del mecanismo de propagación en el contexto del modelo de la subsección II.1 se analiza a continuación).

FUENTE: Elaboración propia con datos desestacionalizados de la STPS.

Gráfica 6 Ciclo largo del empleo nacional: Obserado versus inferido del empleo regional 

3. Limitaciones del análisis

En la sección II mencionamos que la condición de similares que se supone para los componentes cíclicos facilita la descomposición en tendencia y ciclo de las series en el contexto del modelo estructural multivariado. Sin embargo, ello tiene un costo importante, que ahora podemos apreciar mejor, dados los resultados presentados en la sección anterior: esto es, que los ciclos así estimados son no causales en el sentido de Granger.

Para entender mejor la razón de esta limitación basta advertir que la correlación cruzada entre los ciclos de una serie i y de una serie j en el rezago τ es, según ^{Harvey y Koopman (1997)}, ρ_ij (τ) = {ρ^τ cos λτ } ρ_ij (0) para todo i, j = 1,... , N ; en que ρ_ij (0) es la correlación cruzada contemporánea, y ρ y λ son los parámetros de persistencia y duración comunes a todos los ciclos. En consecuencia, para tres series h, i y j del sistema en estudio, tenemos que ρ_hj (τ) /ρ_ij (τ) = ρ_hj (0) / ρ_ij (0), de manera que la importancia relativa de la correlación entre los ciclos de dos series cualesquiera con una tercera, en cualquier rezago, viene dada por la importancia relativa de la correlación contemporánea. De ahí que la especificación con ciclos similares no pueda captar la interacción entre las series.

El análisis anterior nos lleva a concluir que para estimar explícitamente el mecanismo de propagación geográfica de los choques regionales específicos, es necesario hacer grandes cambios en la especificación del modelo estructural multivariado hasta aquí utilizado.⁹ En particular, sería necesario introducir en el modelo (como elemento adicional o en remplazo de los ciclos similares) un vector autorregresivo (VAR); ello es teóricamente posible aunque difícil de instrumentar (^{Harvey y Koopman, 1997}). Estas modificaciones al modelo y el análisis que de ellas se derivarían exceden los objetivos del presente trabajo pero sin duda constituye el objetivo prioritario de nuestra investigación futura.