Introducción

Los trabajos de investigación sobre el enfoque de microestructura aplicados a los tipos de cambio han aumentado de manera exponencial desde que ^{Evans y Lyons (2002)} ofrecieron pruebas congruentes sobre la existencia de una fuerte asociación contemporánea positiva entre los retornos del tipo de cambio y las posiciones netas de los especuladores. Las posiciones netas de los especuladores (order flow) se han definido como el valor neto de las transacciones de divisas iniciadas por el comprador -y por el vendedor- que podrían considerarse como una medida de presión neta de compra. La mayoría de los estudios empíricos acerca de este tema muestran la existencia de un papel explicativo contemporáneo de las posiciones netas de los especuladores en los modelos de tipo de cambio; sin embargo, muy pocos estudios ofrecen una caracterización explícita de la manera en que las posiciones netas de los especuladores transmiten información macroeconómica a los precios de las divisas y por medio de qué canales los impulsos de las posiciones netas de los especuladores contribuyen al mapeo de la información pública para los precios (^{Evans y Lyons, 2006}).

Existen diferentes puntos de vista acerca de los canales de transmisión de las posiciones netas de los especuladores a los tipos de cambio. Entre ellos, tenemos los puntos de vista llamados strong flow-centric y weak flowcentric (^{Froot y Ramadorai, 2005}; ^{Berger, et al., 2008}). El primero propone que las posiciones netas de los especuladores tienen un impacto permanente sobre los tipos de cambio y presentan datos acerca de la información macroeconómica fundamental hacia el mercado, el llamado “canal de información”. El segundo sostiene que las posiciones netas de los especuladores están correlacionadas con las desviaciones temporales del tipo de cambio de su valor fundamental, las cuales podrían provenir de los choques de la demanda de cobertura, los efectos de liquidez o la reacción exagerada de los inversionistas: el llamado “canal de liquidez”. Un punto de vista más integral de dicha relación incorpora tanto a las variables macroeconómicas como a las de la microestructura de mercado y sugiere que las posiciones netas de los especuladores son informativas no sólo acerca de los fundamentos, sino también acerca de los movimientos transitorios de los tipos de cambio (^{Evans y Lyons, 2001}; Baccheta y Van Wincoop, 2006). Este tipo de modelo híbrido surge cuando las posiciones netas de los especuladores ofrecen información relacionada con un efecto de corto plazo, asociado con los efectos de liquidez, y un efecto de largo plazo, que está más asociado con la información acerca de los fundamentos futuros. Las interpretaciones antes mencionadas tienen consecuencias empíricas acerca de la asociación que existe entre los retornos del tipo de cambio y las posiciones netas de los especuladores. El punto de vista strong flow-centric supone que las posiciones netas de los especuladores y los tipos de cambio no son estacionarios, sino que están cointegrados, y que el efecto de las posiciones netas de los especuladores sobre los tipos de cambio es permanente, dado que éstas transmiten información macroeconómica fundamental a los precios. En contraste, los modelos weak flow-centric integran información fundamental, pero no suponen una cointegración.

Estudios empíricos anteriores sobre este tema han cambiado los conjuntos de datos para asegurar la robustez de los hallazgos. En este trabajo, proponemos cambiar el tipo de técnicas que normalmente se emplean para probar el papel que desempeñan las posiciones netas de los especuladores. Utilizamos la metodología SVAR en presencia de variables no estacionarias a fin de poder desenredar los mecanismos de transmisión ocultos y el funcionamiento de los llamados canales “de información” y “de liquidez” del tipo de cambio del peso mexicano/dólar estadunidense. Probamos la validez de un modelo SVAR cointegrado que sugiere que una descripción adecuada de la relación que existe entre las posiciones netas de los especuladores y el tipo de cambio es congruente con el modelo monetario y abarca tanto a las explicaciones basadas en la liquidez como a las explicaciones basadas en la información para el tipo de cambio del peso mexicano/dólar estadunidense. Nuestros hallazgos empíricos sugieren que incluir las posiciones netas de los especuladores en una especificación del modelo monetario estándar aumenta el poder explicativo y la precisión del pronóstico, pero lo más importante es que las posiciones netas de los especuladores están correlacionadas tanto con los fundamentos futuros -como en la versión del modelo monetario de Bilson- (el “canal de información”), como con las noticias de política monetaria (el “canal de liquidez”) (^{Loría y Sánchez, 2010}). En otras palabras, confirmamos que la relación que existe entre el tipo de cambio y las posiciones netas de los especuladores no es incongruente con el enfoque macro para la determinación del tipo de cambio (MAER, por sus siglas en inglés) y que el efecto de las posiciones netas de los especuladores sobre el precio es permanente, mientras que los choques monetarios temporales se transmiten al precio mediante las posiciones netas de los especuladores en la economía mexicana.

Este artículo está organizado de la siguiente manera: en la sección I presentamos el marco teórico. La sección II examina brevemente algo de la literatura reciente relacionada con este tema. En la sección III describimos la metodología SVAR empleada para estimar las respuestas de la divisa mexicana a los choques en las posiciones netas de los especuladores. En la sección IV analizamos la evolución del tipo de cambio nominal en México y su asociación con las posiciones netas de los especuladores. Posteriormente, reportamos nuestros principales hallazgos empíricos y los vinculamos con los hechos estilizados de la economía mexicana. Finalmente, discutimos brevemente nuestros resultados empíricos y algunas implicaciones para las políticas.

I. Las posiciones netas de los especuladores y el enfoque macro para la determinación del tipo de cambio (MAER)

En esta sección presentamos un modelo aumentado de ^{Evans y Lyon (2002)} al incorporar en él algunas variables asociadas con el modelo monetario de determinación del tipo de cambio. De manera más específica, incorporamos las variables y las relaciones sugeridas por una variante clásica del enfoque monetario (MAER) propuesta por ^{Bilson (1978)}, la cual ha probado ser útil para el tipo de cambio mexicano (^{Loria et al., 2010}) y otras economías desarrolladas y en vías de desarrollo (^{Hallwood y MacDonald, 2000}; ^{Chin et al., 2007}). Para hacerlo, podemos empezar ampliando la ecuación fundamental de Evans y Lyon:

(1)

en la que Δe_t representa la variación en el tipo de cambio, Δm_t son las innovaciones relacionadas con la información macroeconómica (los llamados “fundamentos”), λ es una constante positiva, y Δx_t es el cambio en las posiciones netas de los especuladores. En este modelo, el incremento en la información pública asociada con los fundamentos, Δm_t , se define como el cambio en el diferencial de la tasa de interés (es decir, Δm_t = (i − i*)). Dado que Δm_t también podría ser una función de muchos otros fundamentos macroeconómicos, para aumentar la ecuación (1) podemos utilizar el modelo monetario de Bilson en la ecuación (2) que se muestra a continuación.

(2)

donde (m − m), (i − i*) y (y − y*) son los diferenciales de la masa monetaria, la tasa de interés y el ingreso interno real que normalmente se utilizan como los determinantes macro de los tipos de cambio. La ecuación (2) se conoce como la variante fundamental de la ecuación del modelo monetario de Bilson (^{Bilson, 1978}), la cual con frecuencia se ha puesto a prueba mediante una variedad de técnicas econométricas.

Ahora bien, a fin de aumentar el modelo de Evans y Lyon en la ecuación (1), incluimos tanto los fundamentos como las posiciones netas de los especuladores acumuladas (x) en una sola ecuación que incorpora ambos tipos de variables del enfoque macro y una variable del campo de la microestructura de finanzas que transmite información importante al proceso de formación de precios.

(3)

La ecuación (3) representa los mecanismos de transmisión que mantienen al mercado monetario en equilibrio mediante cambios en el tipo de cambio nominal de la siguiente manera: un aumento en los diferenciales de las posiciones netas de los especuladores (x), la masa monetaria (m) o la tasa de interés ocasionarán la depreciación del tipo de cambio Δe>0, y a la inversa, un aumento en los diferenciales del ingreso interno real generará una apreciación Δe<0. Se espera una relación positiva entre las posiciones netas de los especuladores y el tipo de cambio, ya que las compras netas cada vez mayores de la moneda extranjera darán como resultado un precio más alto de ésta en términos de la moneda local. Cabe señalar que las posiciones netas de los especuladores podrían influir directamente en los tipos de cambio, pero también indirectamente al transmitirle choques de información privada al precio.

De esta forma, la ecuación (3) puede verse como una extensión del modelo de Evans y Lyon, dado que adjunta la teoría monetarista de la determinación del precio al primero, a fin de explicar las fluctuaciones en el tipo de cambio nominal. Los movimientos en los agregados macroeconómicos y las posiciones netas de los especuladores afectan la información lo mismo que la liquidez del mercado, y, por lo tanto, el tipo de cambio nominal.

Cabe señalar que esta ecuación implicaría que la relación que existe entre los tipos de cambio y las posiciones netas de los especuladores no es incongruente con el enfoque macro; sin embargo, dado que las posiciones netas de los especuladores comunican información privada (información que no es del conocimiento general), desempeñan el papel de agregar información fundamental para el proceso de formación de precios en los mercados de divisas, y esas posiciones netas de los especuladores ofrecen una variable que influye en el precio, la cual no está reflejada por los fundamentos. La manera específica en que funcionan esos mecanismos es un asunto empírico que trataremos de desenredar en el resto de este artículo.

II. Investigaciones empíricas anteriores sobre modelos que combinan las posiciones netas de los especuladores y el enfoque macro para los tipos de cambio

Hay algunos artículos empíricos que han tratado de determinar las variables que explican el comportamiento del tipo de cambio peso-dólar (^{Loria et al., 2010}; ^{Werner, 1997}; ^{Martínez et al., 2001}; ^{Bazdresch y Werner, 2002}). Estos trabajos han proporcionado algunas evidencias empíricas en favor del enfoque monetario para los tipos de cambio y han identificado algunos fundamentos que podrían haber desempeñado un papel clave en la determinación de la moneda nacional de México. Sin embargo, la literatura existente sobre el tipo de cambio en México no se enfoca en hacer pruebas del papel que desempeñan las posiciones netas de los especuladores en el proceso de formación del precio.

En contraste, existen muchos estudios empíricos que analizan los efectos de las posiciones netas de los especuladores sobre los tipos de cambio para un amplio conjunto de monedas internacionales. Los investigadores han llegado a conclusiones muy distintas sobre este asunto utilizando diferentes metodologías y conjuntos de datos que varían en frecuencia, rango y periodo de cobertura. Por ejemplo, ^{Evans y Lyons (2002)} mostraron que una regresión de los retornos del marco alemán/dólar sobre las posiciones netas de los especuladores diarias dio como resultado un R ² por encima de 60%. Este modelo demostró que los fundamentos macroeconómicos no bastaban para explicar las variaciones en los tipos de cambio y que se necesita algo de información de la microestructura de mercado para explicar la dinámica de los precios de las divisas a nivel mundial.

En el mismo contexto, ^{Froot y Ramadorai (2005)} concluyen que existe una relación positiva entre los retornos del tipo de cambio y las posiciones netas de los especuladores, pero que esto se debe en gran parte a los efectos de liquidez. Específicamente, argumentan que las posiciones netas de los especuladores exhiben más poder explicativo para las variaciones temporales en los tipos de cambio en torno a los niveles de “valor justo”, pero no tienen poder explicativo para las innovaciones en los niveles de valor justo. ^{Breedon y Vitale (2004)} llegaron a una conclusión similar utilizando datos del mercado interbancario de alta frecuencia.

En contraste, Killen et al. (2006) afirman que las posiciones netas de los especuladores están correlacionadas con cambios en el valor fundamental del precio, no sólo con desviaciones temporales, porque transmite información macroeconómica fundamental al mercado. Este hallazgo está asociado con la existencia de un comovimiento de largo plazo (vector de cointegración) entre los diferenciales de las posiciones netas de los especuladores, el tipo de cambio y la tasa de interés en un modelo que utiliza datos diarios del tipo de cambio franco-alemán. Asimismo, ^{Berger et al. (2008)}, mediante el uso de datos detallados al minuto, muestran que existe evidencia en contra de una explicación basada puramente en información de la relación que existe entre las posiciones netas de los especuladores y los tipos de cambio. Sostienen que se pueden obtener mejores modelos de tipo de cambio al combinar los efectos tanto de la liquidez como de la información en los modelos econométricos. Mende y Menkhoff (2003) ofrecen evidencia adicional sobre el tema y también encuentran evidencias de cointegración utilizando datos de los valores mínimos de variación de las posiciones netas de los especuladores de los clientes para el euro/dólar de un banco alemán mediano a lo largo de 87 días bursátiles.

^{Evans y Lyons (2005)} muestran que las posiciones netas de los especuladores parecen tener algo de poder para pronosticar ciertos fundamentos económicos, como el crecimiento del dinero, el crecimiento de la producción y la inflación. Estos resultados sugieren que las posiciones netas de los especuladores proporcionan el vínculo entre los fundamentos y los movimientos en el tipo de cambio mediante un proceso de agregación de la información.

En general, la literatura empírica ha hecho uso de distintas metodologías y fuentes de datos muy diversas para tratar de evaluar la existencia de una relación significativa positiva entre las posiciones netas de los especuladores y los tipos de cambio, lo cual supone que las posiciones netas de los especuladores constituyen el vínculo crucial en el mecanismo por el cual la información privada dispersa en el mercado cambiario extranjero se incorpora en los precios.

III. Asuntos econométricos

En esta sección describimos la metodología SVAR (^{Sims, 1986}; ^{Amisano y Giannini, 1997}) que se utilizará para ofrecer evidencia econométrica confiable sobre la relación que existe entre las posiciones netas de los especuladores y los retornos del tipo de cambio. El principal objetivo de la metodología SVAR es determinar las respuestas dinámicas de distintas variables económicas a las perturbaciones (choques independientes) al combinar análisis de series de tiempo y teoría económica. El enfoque SVAR constituye una buena alternativa para el VAR empírico tradicional (Sims, 1980), ya que la teoría económica desempeña un papel clave en el proceso de creación (identificación) del modelo. El enfoque VAR estándar asume que las variables son estacionarias e incluye únicamente rezagos de todas las variables. Una forma reducida del modelo VAR con un rezago se puede representar de la siguiente manera:

(4)

donde yt es un vector de variables endógenas; dt es un vector de componentes deterministas tales como constantes, tendencias y variables ficticias estacionales o de intervención; y υt es un vector de perturbaciones normales multivariables independientes.

Al principio parece que la ecuación (4) no ofrece ninguna explicación de las relaciones instantáneas (efectos contemporáneos) entre las variables relevantes. En esta ecuación la especificación sólo incluye las variables endógenas rezagadas. Sin embargo, dichos efectos contemporáneos están ocultos en la estructura de correlación de la matriz de covarianza que proviene de υt. Este hecho supone que las innovaciones en υt estarán correlacionadas contemporáneamente.

Un análisis más profundo del llamado VAR primitivo nos lleva a un mejor entendimiento de dicha dificultad (^{Enders, 1995}):

(5)

En la ecuación (5) los errores en εt no tienen una correlación cruzada, ya que la matriz B contiene las interacciones contemporáneas entre las variables. La matriz A encapsula todas las interacciones rezagadas entre las mismas variables.

En consecuencia, el modelo VAR reducido -ecuación (4)- puede ser visto como una reparametrización de la especificación más general dada por el modelo VAR primitivo -ecuación (5)-. De hecho, es fácil ver que C = B ^-1 A y ʋ _t = B ^-1 ε _t ; esto es, los errores del modelo VAR reducido son combinaciones lineales de los choques no correlacionados ε _t .

Entonces, podemos recuperar las interacciones contemporáneas de interés contenidas en la matriz B, siempre y cuando estemos dispuestos a imponer algunas restricciones, distintas de la estructura triangular dada por la descomposición estándar de Cholesky. La descomposición se utiliza para calcular la función impulso-respuesta en un análisis VAR tradicional,¹ lo cual nos permite cumplir las condiciones necesarias para la identificación. Esto establece que el número de elementos distintos de cero en la matriz B debe ser igual o menor que (n ² − n/2). Sin embargo, podemos imponer una descomposición diferente, una matriz que contenga restricciones que nos permitan identificar las interacciones contemporáneas a partir de las perturbaciones de la forma reducida del modelo VAR. Este procedimiento se conoce ampliamente como análisis SVAR.

Un marco de trabajo SVAR más general es el que sugieren ^{Amisano y Giannini (1997)}, que puede admitir una representación VAR con series no estacionarias como el punto de inicio para la especificación de un modelo SVAR. En presencia de la cointegración, la estructuralización del modelo tiene lugar en dos etapas distintas: la primera es la identificación de las relaciones de equilibrio a largo plazo, y la segunda etapa es la identificación de las interacciones a corto plazo.

La estructura final de las ecuaciones instantáneas se logra por medio de dos matrices (A y B) de la siguiente manera:

(6)

(7)

donde ε _t es un vector que incluye las perturbaciones del VAR reducido, y u_t es un vector que incluye las perturbaciones del VAR primitivo. Adicionalmente, sabemos que E(u_t ) = 0 y Eutut'=It. La identificación de las relaciones contemporáneas que existen entre las variables de la ecuación (7) requiere un conjunto de restricciones basadas en supuestos teóricos. La matriz B es una matriz diagonal que normaliza las varianzas de las innovaciones estructurales e_t , y la matriz A contiene las relaciones contemporáneas de interés. La estructura final se obtiene comenzando a partir de un modelo exactamente identificado (una matriz A recién identificada) y moviéndose a una situación de sobreidentificación al imponer restricciones teóricas estadísticamente válidas. La validez de las restricciones impuestas se confirma al utilizar las pruebas de razón de verosimilitud. El uso de la metodología SVAR se puede llevar a cabo en tres pasos. Primero, estimamos el modelo VAR reducido y calculamos una matriz de perturbaciones. Segundo, utilizamos esas perturbaciones para estimar las matrices A y B al utilizar el método FIML (máxima verosimilitud con información completa, por sus siglas en inglés). Tercero, estimamos las reacciones instantáneas del sistema a los choques individuales y graficamos las funciones impulso-respuesta combinando información de los primeros dos pasos. En la sección IV describimos completamente la manera en que la metodología SVAR puede asociarse con una prueba empírica del MAER tanto en el corto como en el largo plazo.

IV. Posiciones netas de los especuladores, fundamentos y el tipo de cambio en México

1. Hechos estilizados

En esta sección utilizamos un modelo SVAR en la presencia de variables no estacionarias para buscar evidencia empírica robusta acerca del papel que desempeñaron las posiciones netas de los especuladores en el proceso de formación de precios durante el periodo de flotación explícita en México que comenzó en 1994. Para empezar, discutimos brevemente algunos de los principales hechos estilizados relacionados con el tipo de cambio peso/ dólar y sus principales determinantes, incluyendo las posiciones netas de los especuladores y algunos de los llamados fundamentos. Nuestros datos consisten en observaciones trimestrales no ajustadas estacionalmente desde 1995.2 hasta 2012.2 del tipo de cambio peso/dólar; las posiciones netas de los especuladores y las diferencias en el logaritmo de la producción nacional y de los Estados Unidos; las tasas de interés; y M2. Las cifras que se muestran a continuación representan el comportamiento de dichas series.

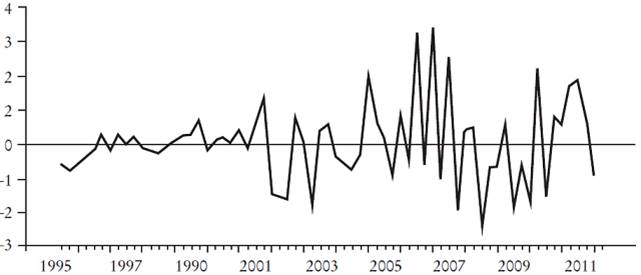
Un análisis de la Gráfica 1 sugiere que el tipo de cambio nominal en México ha pasado por distintas etapas. Primero, podemos ver un camino creciente aunque con dos periodos de estabilidad. Dichas tendencias tenían relación con la independencia del Banco Central de México en 1993 y la adopción del régimen actual de tipo de cambio flotante como una respuesta a las difíciles circunstancias generadas por la crisis financiera. Desde entonces, el régimen de tipo de cambio flotante ha continuado y la política monetaria se ha enfocado en la estabilidad macroeconómica y el control de la inflación.

Gráfica 1: Logaritmo del tipo de cambio nominal (peso/dólar), datos trimestrales 

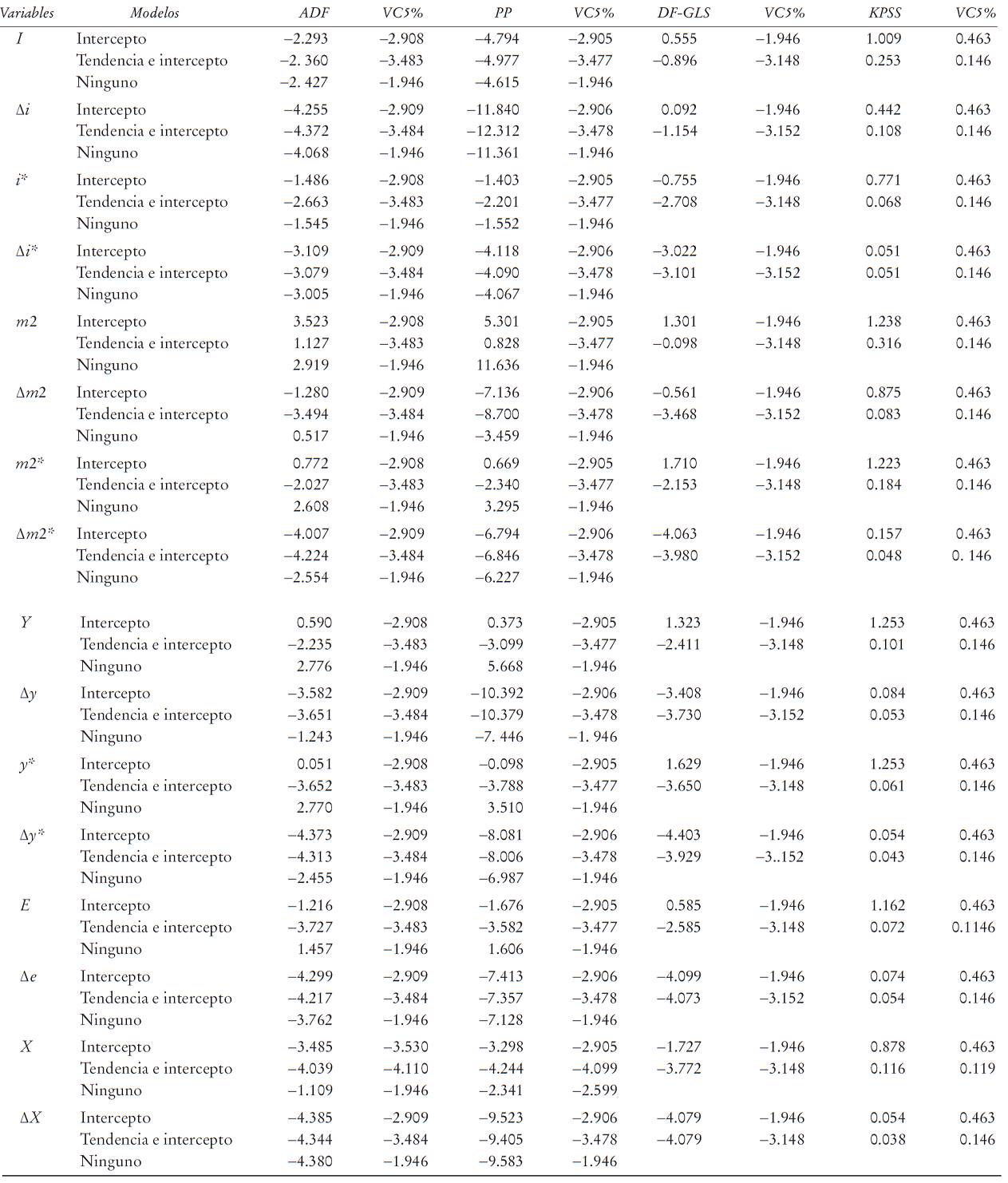
Hacemos ahora una prueba para detectar la presencia de las raíces unitarias en el tipo de cambio nominal, las posiciones netas de los especuladores, la producción extranjera y nacional, las tasas de interés, y las masas monetarias. El Cuadro 1A del Apéndice sugiere que todas las variables son variables integradas de orden uno, I(1), lo que implica que modelarlas en niveles puede llevar a conclusiones engañosas, a menos que se cointegren. La prueba de raíz unitaria nos permite concluir que todas las variables son I(1), especialmente las posiciones netas de los especuladores.

La Gráfica 2 sugiere que las posiciones netas de los especuladores y el tipo de cambio nominal están positivamente correlacionados, lo que indica que el precio aumenta con la presión de compra. La línea punteada representa las posiciones netas de los especuladores lo largo del tiempo respecto de las transacciones interbancarias consumidas. Por otro lado, las Gráficas 3, 4 y 5 sugieren que los diferenciales extranjeros y nacionales siguen tendencias similares con el tiempo, lo que supone la existencia de una o más relaciones de largo plazo. De hecho, el Cuadro 2A del Apéndice muestra que los diferenciales entre las variables de México y los Estados Unidos son estacionarios. Por lo tanto, existe la posibilidad de encontrar una cointegración entre las variables y de especificar un modelo VAR cointegrado como el punto de inicio de nuestro análisis estructural (SVAR); lo que nos permitiría no sólo determinar si el poder explicativo del modelo macro aumenta con las posiciones netas de los especuladores, sino también tener una idea general de la manera en que las posiciones netas de los especuladores transmiten información al precio en un escenario multivariable.

Gráfica 2: Logaritmo del nivel de tipo de cambio nominal (e) y posiciones netas de los especuladores (X) 

Gráfica 3: Logaritmo del nivel de las tasas de interés de los Estados Unidos y México 

Gráfica 4: Los Estados Unidos y México: logaritmo del nivel del PIB 

Gráfica 5: Los Estados Unidos y México: logaritmo del nivel de M2 

2. Métodos

Esta sección describe la metodología empírica para probar la relevancia de las posiciones netas de los especuladores para la determinación del tipo de cambio y su papel en la transmisión de la información al precio mediante el uso de un modelo SVAR cointegrado. En este contexto, primero mostramos cómo podemos usar un modelo SVAR para describir la manera en que las posiciones netas de los especuladores transmiten información privada al precio en el contexto de un modelo monetario, el cual incluye como fundamentos los diferenciales de tasa de interés, producción y masa monetaria.

En general, nuestro procedimiento de prueba no sólo implica estimar la ecuación de cointegración del tipo de cambio a largo plazo asociada con la ecuación teórica del tipo de cambio -ecuación (3)-, sino también imponer restricciones en la matriz de covarianza de la forma reducida del modelo VAR cointegrado para calcular la correlación contemporánea que existe entre las variaciones de las posiciones netas de los especuladores y del tipo de cambio y los canales de transmisión relevantes en el corto y el largo plazo.

En presencia de raíces unitarias, la estructuralización de un modelo VAR se puede llevar a cabo en tres etapas distintas. El primer paso supone especificar una representación VAR adecuada para el conjunto de variables, lo cual implica elegir el orden de rezago, el rango de cointegración y el tipo de polinomios determinantes asociados, así como una identificación sensible del espacio que abarcan los vectores de cointegración (^{Johansen, 1995}). Si una de las relaciones de cointegración identificadas es congruente con los coeficientes sugeridos por la ecuación (3), podemos concluir que las posiciones netas de los especuladores desempeñan un papel importante en la explicación del comportamiento del precio en el largo plazo. De manera más específica, probamos la existencia de una relación de cointegración estadísticamente sólida que incluye las posiciones netas de los especuladores, lo cual puede relacionarse con la siguiente ecuación del tipo de cambio de largo plazo:

(8)

Si las posiciones netas de los especuladores tienen una influencia permanente sobre la determinación del tipo de cambio en esta especificación de largo plazo, β₄ debe ser positivo. Por otro lado, la variante del enfoque monetario de Bilson para la determinación del tipo de cambio es válida cuando los signos del coeficiente esperado de largo plazo son β ₁ > 0, β ₂ < 0 y β ₃ > 0 (^{Chin et al., 2007}).

En el segundo paso, la etapa de “estructuralización”, utilizamos el modelo VAR en su forma de corrección de errores (VECM, por sus siglas en inglés) para identificar las asociaciones de muy corto plazo entre los cambios de tipo de cambio y las posiciones netas de los especuladores, lo cual está oculto en la matriz de covarianza de los residuos de dicho modelo multivariable. Es decir, nuestro punto de inicio para la estructuralización es la siguiente representación VAR cointegrada de la ecuación del tipo de cambio.

(9)

donde

y

A fin de recuperar los coeficientes del modelo de corto plazo podemos usar la matriz de varianza-covarianza del VAR en su forma de corrección de errores (9). Luego, con base en la ecuación (7) podemos probar la validez estadística de canales de transmisión muy distintos entre las posiciones netas de los especuladores y las tasas de interés. Por ejemplo, en este trabajo, buscamos determinar la validez de corto plazo de la ecuación (3) mediante la descomposición de la siguiente matriz, lo cual probaremos en la siguiente sección.

Restricciones SVAR de corto plazo

(10)

Este conjunto de restricciones corresponde a los siguientes canales de transmisión de corto plazo:

Gráfica 6: Vínculos instantáneos en el modelo de tipo de cambio 

Esta estructura de matriz puede reescribirse como las siguientes ecuaciones relacionadas con el modelo monetario de corto plazo, incluyendo las posiciones netas de los especuladores:

(11)

(12)

(13)

(14)

(15)

Para que el modelo monetario desempeñe un papel relevante en el proceso de formación del precio, los signos del coeficiente esperado de corto plazo deben ser ∂εe/∂εm-m*=a51> 0, ∂εe/∂εi-i*=a52 > 0, ∂εe/∂εy-y*=a32*a53< 0 (^{Chin et al., 2007}). Además, un impacto significativo de corto plazo de las posiciones netas de los especuladores sobre el precio, es decir, ∂εe/∂εX=a41*a54 > 0, supone que los choques monetarios temporales transmiten algo de información al precio mediante las posiciones netas de los especuladores. Cabe mencionar que el modelo debe estar identificado o sobreidentificado y la validez de las restricciones impuestas de largo y corto plazo deben confirmarse mediante el uso de pruebas de razón de verosimilitud.

Finalmente, la validez de corto y mediano plazo del modelo monetario también puede verificarse mediante una modelación plausible de las correlaciones instantáneas mediante funciones impulso-respuesta.

3. Resultados empíricos y discusión

Por lo tanto, para el análisis econométrico, estimamos un modelo VAR estadísticamente adecuado (^{Spanos, 1986})² con variables no estacionarias de 1995.2 a 2012.2. Utilizamos datos trimestrales en logaritmos de tipo de cambio nominal peso/dólar (e), posiciones netas de los especuladores (x) y en logaritmos de variables nacionales y extranjeras como: producción (y, y*), tasas de interés (i, i*) y M2 (m, m*). El modelo VAR incluye una constante no restringida y una tendencia restringida, un rezago y cuatro variables ficticias que captan los efectos de los choques financieros de 1995, 2008, 2009 y 2012. Las pruebas de raíz unitaria y las pruebas de mala especificación individuales y conjuntas se muestran en los Cuadros 1A, 2A, 3A y 4A del Apéndice. El número de rezagos se eligió con base en motivos de adecuación estadística, sin embargo, también utilizamos pruebas como la del criterio de información de Schwarz, la prueba de Godfrey Portmanteau y la prueba RV (esta última con una pequeña corrección de la muestra sugerida por ^{Sims, 1980}). Todas las pruebas de mala especificación se reportan en el Apéndice.

A continuación procedemos a hacer la prueba del rango de cointegración utilizando la metodología del rango reducido de Johansen. La traza estadística que se presenta a continuación en el Cuadro 1, sugiere la existencia de tres o cuatro vectores de cointegración (^{Johansen, 1988}).

^a r = cualquier entero entre 0 y el número de variables endógenas, y p - r = cualquier entero entre 0 y el número de variables endógenas menor r.

Cuadro 1: Prueba del Rango de Cointegración de Johansen 

A fin de ofrecer evidencia adicional en este asunto, también aplicamos el procedimiento de prueba secuencial sugerido por ^{Johansen (1995)} para la determinación conjunta del rango de cointegración y la tendencia polinomial³ en el siguiente Cuadro 2. En primer lugar, reportamos la prueba de componentes determinantes (constante y tendencia) y luego la prueba conjunta (estadística).

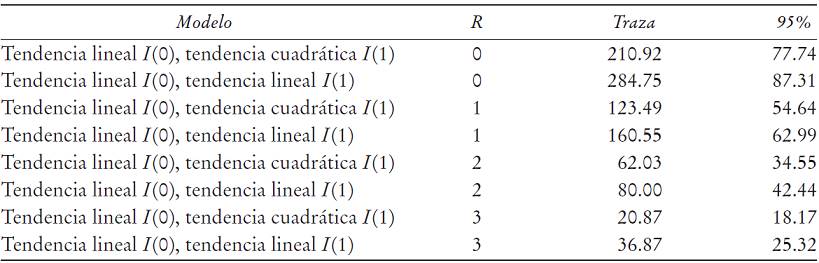
^a r = rango de cointegración.

Cuadro 2: Estrategia de la prueba secuencial de ^{Johansen (1995)} para la determinación conjunta del rango de cointegración y el polinomio determinante 

Los resultados sugieren la existencia de máximo cuatro vectores de cointegración al nivel de confianza habitual de 5% e indican que un modelo sensible implica la existencia de una tendencia lineal en la relación de cointegración en los niveles de las series. Con el fin de asegurar la robustez de nuestros resultados del rango de cointegración a través del tiempo, utilizamos el procedimiento iterativo de ^{Hansen y Johansen (1993)}. La Gráfica 7 muestra los resultados de las pruebas. Estas pruebas refuerzan la hipótesis de que existen tres relaciones de cointegración estables a través del tiempo al nivel de significancia de 95% (modelo R).

^a La línea superior representa la prueba de la hipótesis r = 0, que en este caso está rechazada para cualquier tamaño de muestra, ya que la relación de la prueba con el valor crítico de 95% es mayor que uno. La segunda línea de arriba representa la prueba para r ≤ 1, y así sucesivamente. Las cifras claramente muestran que r = 1 se selecciona para cualquier tamaño de muestra.

Gráfica 7: Pruebas de Hansen y Johansen^a 

Dado que el procedimiento de máxima verosimilitud de Johansen estima sólo una base para el espacio de cointegración, el problema de identificación permanece abierto. Una manera útil de tratar el problema de la identificación es imponer un conjunto de restricciones creíbles a priori sobre el espacio del parámetro. En este caso, normalizamos el primer vector de cointegración como una ecuación del tipo de cambio de largo plazo y consideramos la hipótesis de que las diferencias que existen entre las variables nacionales y extranjeras son estacionarias; así, esas restricciones nos permiten tener una identificación sensible del espacio distribuido por el vector de cointegración.⁴ A continuación se reporta la ecuación de cointegración estimada.

Estadístico t entre paréntesis.

Cuadro 3: Vector de cointegración normalizado 

Ésta es una de las posibles maneras de escribir el vector de cointegración que implica que existe una relación de largo plazo asociada con la versión del modelo monetario de Bilson, pero incluyendo las posiciones netas de los especuladores como un determinante del precio a largo plazo. En esta particular interpretación del espacio de cointegración podemos ver que una relación positiva entre las posiciones netas de los especuladores y el precio se mantiene en el largo plazo. La Gráfica 8 también confirma que la ecuación de largo plazo, que es una combinación lineal del tipo de cambio y sus determinantes, tiene un comportamiento estacionario tal como sugiere el modelo monetario. La Gráfica 7 muestra la estabilidad del vector de cointegración; en otras palabras, no tiene ningún cambio estructural. Esta relación de cointegración de largo plazo confirma que las posiciones netas de los especuladores tienen un efecto permanente y transmiten información macroeconómica fundamental al mercado, tal como lo sugiere el punto de vista strong flow-centric. Podemos determinar que las posiciones netas de los especuladores están correlacionadas con los fundamentos futuros, como en la versión del modelo monetario de Bilson, y que la relación que existe entre el tipo de cambio y las posiciones netas de los especuladores no son incongruentes con el enfoque macro para la determinación del tipo de cambio. En otras palabras, con este resultado, podemos concluir que las posiciones netas de los especuladores tienen un efecto permanente sobre el tipo de cambio. Lo importante es conocer la manera en que la información se transmite al mercado cambiario. El modelo SVAR proporciona el mecanismo de transmisión.

Gráfica 8: Vector de cointegración del tipo de cambio (VC) 

Para estimar las interacciones contemporáneas de interés asociadas con los coeficientes, la ecuación (3), utilizamos las restricciones que sugiere la ecuación (10) y las incluimos en las matrices A y B para obtener la estructuralización sugerida por las ecuaciones (11), (12), (13), (14) y (15). Cabe señalar que para llegar a dichas restricciones comenzamos con una estructura identificada que es dada exactamente por la descomposición triangular menor de la matriz de varianza-covarianza de las perturbaciones VAR estimadas. Entonces, en la matriz A mantenemos los coeficientes que nos permiten identificar el MAER, siempre y cuando sean estadísticamente significativos, y restringimos los parámetros no significativos a cero, lo que nos lleva a una situación de sobreidentificación.⁵ Finalmente, aseguramos la validez de las restricciones anteriores impuestas por medio de una prueba RV, y las ecuaciones (16) a (20) muestran las estimaciones de las interacciones contemporáneas que representan la versión corta del modelo monetario. Cabe mencionar que las estimaciones finales respaldan la representación gráfica de las relaciones instantáneas entre nuestras variables que se muestran en la Gráfica 6.

El Cuadro 4 sugiere que un choque de política monetaria que genere más liquidez en el mercado depreciará el tipo de cambio directa e indirectamente a través de las posiciones netas de los especuladores que transmiten información útil para la determinación del precio. La tasa de interés afecta el tipo de cambio directa e indirectamente al afectar los diferenciales de producción, lo cual transmite información a los mercados. Estos resultados estadísticos confirman que las posiciones netas de los especuladores transmiten choques monetarios al mercado en el muy corto plazo. Específicamente, en el caso de México podemos concluir que las posiciones netas de los especuladores transmiten los choques de la masa monetaria al mercado cambiario.

Cuadro 4: Efectos estimados contemporáneos 

(16)

(17)

(18)

(19)

(20)

Estimación por MV, errores estándar entre paréntesis, prueba de sobreidentificación, prueba RV: X ² ( 4.0000 ): 9.0237, Prob: 0.0605

(21)

(22)

(23)

(24)

La validez estadística del mecanismo que se muestra en el Cuadro 4 confirma nuestras suposiciones a priori acerca de las conexiones a muy corto plazo entre los fundamentos y el tipo de cambio: el impacto de los choques estructurales monetarios y de interés sobre el tipo de cambio nominal son positivos; y a la inversa, el impacto de un choque estructural de producción es negativo. Finalmente, los choques monetarios temporales también tienen una influencia positiva sobre el tipo de cambio a través de las posiciones netas de los especuladores. Nuestras simulaciones también muestran que las posiciones netas de los especuladores tienen un efecto contemporáneo sustancial sobre el tipo de cambio debido a que los choques de la masa monetaria afectan el tipo de cambio a través de las posiciones netas de los especuladores. De manera que las posiciones netas de los especuladores están correlacionadas con las noticias sobre política monetaria y el canal de liquidez, lo que confirma que los choques monetarios temporales se transmiten al precio a través de las posiciones netas de los especuladores.

Podemos ofrecer más evidencia sobre dichos mecanismos al hacer uso de técnicas de simulación típicas, tales como las funciones impulso-respuesta (FIR) con base en el modelo VAR estimado y restringido para satisfacer la restricción sobre el rango de cointegración. A continuación se muestran las FIR y sus respectivos intervalos de confianza asintóticamente válidos.

En la Gráfica 9 se muestran las respuestas del tipo de cambio a los choques en la masa monetaria, el diferencial de la producción y el diferencial en la tasa de interés, respectivamente. Las Gráficas 9a y 9b muestran que las innovaciones a los diferenciales entre los agregados monetarios nacionales y extranjeros y las tasas de interés tienen un impacto positivo inmediato sobre el tipo de cambio, mientras que una innovación a la producción nacional tiene un efecto negativo rezagado sobre el tipo de cambio peso/dólar (Gráfica 9d). Esto confirma nuestros hallazgos sobre los choques contemporáneos y nos permite decir que el MAER ofrece un buen marco de trabajo para entender el comportamiento de la moneda mexicana. En resumen, nuestros hallazgos empíricos revelan que los movimientos del tipo de cambio a final de cuentas responden a los choques fundamentales como la variante del MAER de Bilson. También cabe destacar que, de acuerdo con la Gráfica 9c, las posiciones netas de los especuladores tienen un efecto positivo sobre el tipo de cambio, tal como se predijo en nuestra hipótesis inicial.

Gráfica 9: Función impulso-respuesta de los efectos estructurales 

Claramente podemos ver el mecanismo de transmisión de las posiciones netas de los especuladores al mercado cambiario. Es importante mencionar que las posiciones netas de los especuladores toman información de la política monetaria (m - m*) a fin de tener un efecto de tipo de cambio, así que podemos concluir que el punto de vista weak flow-centric se comprueba. Como verificamos anteriormente, esto implica que las posiciones netas de los especuladores están correlacionadas con las desviaciones temporales del tipo de cambio a partir de su valor fundamental, que podría provenir de los choques de la demanda de cobertura -que en este caso es la política monetaria-.

Finalmente, el Cuadro 5 muestra que el poder explicativo de las posiciones netas de los especuladores es mayor que el del resto de los fundamentos. Además, una prueba de tipo F indica que no deberíamos excluir las posiciones netas de los especuladores de nuestro modelo SVAR, ya que ayudan a aumentar la idoneidad del modelo.⁶ El Cuadro 6 muestra que la precisión del pronóstico mejora una vez que introducimos las posiciones netas de los especuladores en el sistema VAR. Esto supone que las posiciones netas de los especuladores son necesarias para explicar el comportamiento a largo plazo del tipo de cambio de México.

Cuadro 5: Análisis de R² para cada ecuación del modelo VAR 

Cuadro 6: Errores de pronósticos fuera de las muestras (raíz cuadrada de los errores cuadráticos medios) 

Conclusiones

Nuestra evidencia empírica ofrece una caracterización explícita de la manera en que las posiciones netas de los especuladores transmiten información privada al precio y mediante qué canales los impulsos de las posiciones netas de los especuladores contribuyen al mapeo de dicha información. Utilizamos un modelo SVAR cointegrado para mostrar que una descripción adecuada de la relación que existe entre las posiciones netas de los especuladores y el tipo de cambio es congruente con el modelo monetario y abarca tanto a las explicaciones basadas en la liquidez como a las explicaciones basadas en la información. Esto es, incluir las posiciones netas de los especuladores en la especificación de un modelo monetario aumenta el poder explicativo y la precisión del pronóstico, pero de manera más importante, las estimaciones de largo plazo muestran que las posiciones netas de los especuladores tienen un efecto permanente y transmiten información macroeconómica fundamental al mercado, la cual se incorpora en los precios por medio de las posiciones netas de los especuladores. Podemos ver esto con el vector de cointegración, que muestra las relaciones que existen entre el tipo de cambio y las otras variables (m, m*, i, i* y x) en el largo plazo, demostrando así que las posiciones netas de los especuladores tienen un efecto permanente.

Por otro lado, mostramos que las posiciones netas de los especuladores tienen un efecto temporal sobre el tipo de cambio. Esto se demuestra con el modelo SVAR. Esta técnica nos permite describir el mecanismo de transmisión de las posiciones netas de los especuladores al mercado cambiario. Nuestros resultados muestran que las posiciones netas de los especuladores tienen un efecto contemporáneo sustancial sobre el tipo de cambio debido a que los choques de la masa monetaria afectan el tipo de cambio mediante las posiciones netas de los especuladores.

En conclusión, las posiciones netas de los especuladores están correlacionadas tanto con los fundamentos futuros, como en el caso del MAER (el canal de información), como con las noticias de la política monetaria (el canal de liquidez). Este hallazgo confirma que la relación que existe entre el tipo de cambio y las posiciones netas de los especuladores no es incongruente con el enfoque macro para la determinación del tipo de cambio (MAER), y que los choques monetarios se transmiten al precio a través de las posiciones netas de los especuladores. Claramente podemos afirmar que las posiciones netas de los especuladores transmiten información no visible al mercado de intercambio de divisas, así que nos permite entender mejor su comportamiento.