Introducción
El estudio de la determinación de los salarios es abundante en la bibliografía sobre economía laboral. En general, de acuerdo con la teoría económica, los salarios de las personas deberían ser determinados únicamente por su productividad (Becker, 1964; Mincer, 1974). Sin embargo, no siempre es fácil establecer la productividad de cada trabajador. Por otro lado, existe una línea de pensamiento que establece que los salarios son en realidad un reflejo del capital humano, debido a un asunto de señalización y no de su productividad (Spence, 1973).
Empíricamente, se ha observado que existen razones adicionales a la productividad marginal y a la señalización de por qué los salarios difieren en el mercado laboral. Entonces, estas diferencias que no corresponden a las capacidades o la productividad de las personas nos indican que estamos en presencia de discriminación salarial (Fuentes, Palma y Montero, 2015).
Si bien estudiar la desigualdad y la brecha salarial entre hombres y mujeres, así como realizar esfuerzos por disminuirlas -puesto que ello tiene efectos positivos en la productividad- es importante para reducir la pobreza, también es necesario por respeto a los derechos y armonía social (Organización Internacional del Trabajo [OIT], 2018). Por otro lado, asimismo se tienen implicaciones económicas. En particular la igualdad de género en educación y empleo contribuye al crecimiento económico y al desarrollo, pero el efecto varía entre países según su nivel de ingresos y la estructura de su economía (Kabeer y Natali, 2013). En el trabajo de Kabeer y Natali (2013: 20), en cuanto a la igualdad salarial los autores llegan al siguiente resultado: “A medida que los países ascienden en la cadena de valor y se desarrollan los mercados nacionales, la ‘brecha salarial óptima’ debería comenzar a disminuir y converger finalmente hacia cero”.
Además, si el retorno esperado a la inversión de capital humano (educación y experiencia, entre otras variables relevantes) es menor para un grupo -en este caso las mujeres-, cuando éste decida cuánto invertir en su capital humano, escogerá un nivel inferior al del resto, lo cual en el largo plazo reducirá su capacidad de generar ingresos de forma autónoma y ocasionará un retraso importante en su propio desarrollo y el de la sociedad en su conjunto. Esto constituye una barrera importante para la asignación eficiente de recursos dentro de una economía (Fuentes et al., 2015). Cabe destacar que la discriminación como concepto puede surgir por diversas razones: por origen social, etnia, raza, idiomas u otras. En Chile el fenómeno que ha llamado la atención en los últimos años es la discriminación salarial por género, la cual se estudia en este documento.
En este trabajo se utilizan datos de la Encuesta de Caracterización Socioeconómica Nacional (Casen) para el periodo de 1990 a 2017 con el fin de explorar y cuantificar la brecha de género en los salarios por hora de los trabajadores, además de estudiar qué parte de esta brecha corresponde a discriminación salarial mediante el método original de descomposición de Blinder-Oaxaca, así como por medio de distintas versiones de esta metodología, las cuales separan la brecha salarial en un componente asociado con dotaciones, características o conocimientos (la parte explicada de la brecha salarial) y otro con coeficientes (la parte no explicada de la brecha salarial), que puede indicar discriminación. Puesto que se usarán ecuaciones de salarios, es importante considerar que se estará incurriendo en un sesgo de selección, ya que el grupo de la población que no trabaja y no recibe un salario no se considera en la estimación. Para solucionar este problema, se utilizará el método desarrollado por Heckman (1977). Finalmente, se usa la metodología de Melly (2006) para estimar la descomposición de Blinder-Oaxaca, pero por cuantil de ingreso, y así observar no sólo la discriminación salarial en el valor promedio, sino a lo largo de toda la distribución de ingresos. Esto con el fin de responder una pregunta importante en la literatura del último tiempo sobre la discriminación salarial de género: ¿las mujeres enfrentan un “techo de cristal” o un “piso pegajoso”? (Deshpande, Goel y Khanna, 2018).
Este trabajo contribuye a la literatura al mostrar la brecha salarial de Chile y qué parte de ésta se puede explicar debido a discriminación salarial pura. Este tema no había sido actualizado en la última década mediante control por diferencias regionales y diferencias entre el ámbito rural y urbano, entre otras. Además, se muestra la comparación de cuatro versiones distintas del modelo original de Blinder-Oaxaca, con y sin corrección por sesgo de selección, para mostrar sus diferencias y evaluar qué tan sobrestimada o subestimada está la discriminación salarial cuando no corregimos este problema. Finalmente, este trabajo detalla un poco más la brecha de género sin centrarse únicamente en la brecha salarial, sino también en la brecha en el acceso al mercado del trabajo y en el nivel educativo, además de detallar con mayor precisión sus componentes y consecuencias.
Los resultados más importantes de este trabajo muestran que la primera gran brecha de género se encuentra en la participación laboral, la cual muestra que los hombres tenían 55.7% más de participación laboral que las mujeres en 2017 (74.7% de los hombres frente a 48% de las mujeres). Si bien es una brecha muy alta, es importante mencionar que ha disminuido considerablemente en los últimos años. Por otro lado, la brecha salarial siempre ha estado en favor de los hombres en Chile, situándose en 9.8% en 2017. En cuanto a los años de educación, se visualiza que es muy diferente cuando se observan las personas con empleo y las desempleadas. Para 2017, los hombres con empleo tenían 8.9% años menos de estudios que las mujeres con empleo. En el caso de los desempleados, para el mismo año se observa que los hombres sin empleo tenían 4.3% más años de educación que las mujeres en una situación similar. Esto indica que las mujeres requieren más años de educación que los hombres para obtener un empleo, pero reciben un salario menor al de ellos. Al corregir por sesgo de selección, se observa que la estimación de la discriminación salarial sin corrección por este problema lo subestimaba en gran medida. Se estima que la discriminación para 2017 alcanzó 49.7%, que se puede separar en 4.5% relacionado con el favoritismo de los hombres y 45.2% relacionado con la discriminación pura contra las mujeres.
En cuanto a una perspectiva histórica, hasta 2003 la discriminación salarial venía disminuyendo casi ininterrumpidamente desde 1990, y para las investigaciones de esa época era fácil pensar que la brecha seguiría cayendo (Fuentes et al., 2015). En este trabajo se muestra que tal conclusión es errada, puesto que entre 2003 y 2017 la discriminación salarial se estancó en Chile; prueba de esto es que en 2017 se obtuvieron casi los mismos resultados que en 2003 (80.3% en 1990, 52.6% en 2003 y 49.7% en 2017). Por otro lado, en todo el periodo estudiado se observa que el mayor componente de la brecha salarial es el subpago que reciben las mujeres, también llamado discriminación pura, y, en mucha menor medida, el sobrepago, asimismo llamado favoritismo, que reciben los hombres.
Finalmente, este trabajo, aunque de manera más superficial, muestra que casi toda la discriminación salarial se encuentra en los extremos más pobres y más ricos cuando separamos por cuantiles de ingreso. Específicamente, la discriminación está presente principalmente en 10% de la población de menores y 10% de mayores ingresos. Además, muestra que la variable más relevante que compone la discriminación salarial es la experiencia laboral, mientras que los años de educación ayudan a disminuirla.
El trabajo se organiza de la siguiente manera: en la sección I se realiza una breve revisión de la literatura; la sección II explica las técnicas de descomposición de las diferentes metodologías y cómo se corrige por sesgo de selección; la sección III describe los datos y presenta estadísticas descriptivas separadas por género y las brechas laboral y salarial presentes en Chile; la sección IV contiene los resultados de las descomposiciones, y, finalmente, en la sección V se concluye.
I. Revisión de la literatura
La literatura sobre la brecha y la discriminación salarial en Chile no es tan amplia como en otros países más desarrollados.
En el contexto de las brechas salariales, es importante mencionar que un factor relevante en temas de género es la carencia de políticas públicas que den soporte al trabajo familiar, como guarderías o lugares públicos para el cuidado de adultos mayores. El informe de la Organización de las Naciones Unidas (ONU, 2018) muestra que un primer paso hacia la igualdad en este sentido son las leyes y las políticas. Así, Bosch, García, Manríquez y Valenzuela (2018) encuentran que un aumento de conciliación familiar, usando como indicador el acceso a las guarderías facilitado por el gobierno, tiene importantes efectos positivos en la participación laboral femenina, e incluso incrementos en el producto interno bruto (PIB). El informe de la OIT (2018) muestra que el principal motivo de la brecha salarial es que las mujeres cuentan con mayor tasa de empleo parcial y empleos socialmente menos valorados.
En Chile, trabajos como el de Meller, Valdés y Lara (2011) analizaron la brecha salarial con una base de datos del Ministerio de Educación, aunque solamente para profesionales y sin mayores detalles de descomposición. En este trabajo los autores realizan una regresión clásica de Mincer con la que usan una variable binaria para indicar el género de la persona y las clásicas variables de control, y encuentran una brecha salarial de 22% en contra de la mujer.
Por otro lado, como se mencionó en la sección anterior, la discriminación puede ser por motivos distintos a la diferencia de género e incluso en otros aspectos diferentes al salario; además, es posible que no toda la brecha salarial se deba a la discriminación en el mercado laboral, por lo cual es importante realizar una descomposición de dicha brecha si se quiere hablar seriamente de discriminación en este contexto. En tal sentido, Ferrada y Montaña (2014) usaron la encuesta Casen entre 1990 y 2009 y la descomposición original de Blinder-Oaxaca como metodología corrigiendo por sesgo de selección. Ellos: 1) estudian la brecha salarial entre dos regiones de Chile, la de Magallanes, considerada “zona extrema” (lo cual aumenta sus salarios mediante bonificaciones gubernamentales), y la Región Metropolitana (capital del país), y 2) comparan si la estructura de las brechas regionales de las mujeres es igual a las de los hombres. Encuentran que, hay una brecha en contra de las mujeres en Magallanes de 16.7%: 8.6% corresponde a las diferencias en dotación y 8.1% a las diferencias en rendimiento. Para los hombres, hay una brecha a favor en esta región de 1.3%: -2.3% corresponde a las diferencias en dotación y 3.6% a las diferencias en rendimiento. Otro trabajo importante en el contexto de Chile es el de Montero y Garcés (2009), en el cual los autores descomponen la brecha salarial en contra de la población indígena con datos de la encuesta Casen entre 1996 y 2006, la metodología de Blinder-Oaxaca y versiones posteriores corrigiendo por sesgo de selección. Encuentran que en el periodo estudiado la discriminación total sufrida por la población indígena ha pasado de 15% en 1996 a 12.5% en 2006, y que el mayor componente se encuentra en la discriminación pura. Siguiendo esta misma idea, Zapata y Cid (2009) estudian la brecha salarial y la discriminación de salarios específicamente en contra de la etnia mapuche en Chile mediante la metodología de Blinder-Oaxaca, también corrigiendo por sesgo de selección y usando la Casen entre 2000 y 2006 como fuente de datos. Ellos encuentran que existe discriminación salarial para hombres de esta etnia, la cual no aumentó en el periodo estudiado, pero no se encuentran resultados significativos para mujeres.
Si nos centramos en el estudio y la descomposición de la brecha salarial entre hombres y mujeres en Chile, Fuentes et al. (2015) realizan un trabajo similar a éste solamente con el modelo original de Blinder-Oaxaca y el trabajo de Oaxaca y Ransom (1994), que incorpora la corrección por sesgo de selección. Los autores también usan los datos de la encuesta Casen, pero únicamente de 1990 a 2003. Hasta ese año se encuentran resultados consistentes con este trabajo. Ellos concluyeron que la disminución salarial se daba desde 1990. En este trabajo, al actualizar la información hasta la encuesta de 2017, se muestra que la discriminación salarial no continuó cayendo luego de 2003, sino que se estancó en estos niveles, es decir, en Chile en 2017 ésta es aproximadamente la misma que había en 2003.
Perticará y Astudillo (2010) agregan la metodología de descomposiciones por cuantiles de ingreso, también para el caso chileno, pero estiman la brecha salarial de Chile de 2002 a 2006 con la Encuesta Nacional de Protección Social de Chile, en lugar de la Casen. Los autores encuentran que el efecto de las características en la brecha (su parte explicada) es muy pequeño y estadísticamente no significativo hasta la mediana, donde se hace favorable a las mujeres y crece de forma constante hasta llegar a alrededor de 12% en el percentil 90. Por otro lado, el efecto de los coeficientes (la parte no explicada) es siempre en favor de los hombres en toda la distribución, sin encontrar un “techo” para este efecto. Por último, muestran que las mayores brechas se hallan entre los trabajadores del comercio y los agrícolas calificados.
En el contexto de América Latina para la descomposición por cuantiles, Arceo-Gómez y Campos-Vázquez (2014) estudian la descomposición de la brecha salarial para México de 1990 a 2010 mediante datos censales. Los autores se centran principalmente en la descomposición por cuantiles de ingreso controlando por sesgo de selección, y muestran las diferencias entre los cuantiles altos y bajos, en áreas urbanas y rurales. Concluyen que la brecha salarial ha disminuido para el periodo estudiado usando la corrección, pero esta disminución se centra en la parte alta de la distribución de ingresos y no en la baja. Encuentran evidencia de un “piso pegajoso” en las personas con baja escolaridad y un efecto “techo de cristal” en la parte alta de la distribución salarial, las mismas personas que tienen alta escolaridad. Para Ecuador en 2010, Anglade, Useche y Deere (2017) estiman la brecha de riqueza por cuantiles entre hombres y mujeres. Encuentran que en los primeros cuantiles la brecha de género se asocia principalmente con diferentes rendimientos de las covariables; en cambio, en los cuantiles medios y superiores las diferencias de género se centran en las dotaciones: propiedad de las cuentas de ahorro, educación y edad. Finalmente, Yahmed (2018) estudia cómo la brecha salarial por género difiere entre trabajadores formales e informales para las zonas urbanas de Brasil en 2015. Con las metodologías de descomposición de brechas salariales, al corregir por sesgo de selección, encuentra que las brechas salariales para ambos grupos, trabajadores formales e informales, es de 7.6 y 5%, respectivamente. Además, separa su estudio por nivel educativo: primario o menos, secundario, y terciario. Encontró que las mujeres con empleo tienen menores características observables -por ejemplo, nivel de estudios- que los hombres con empleo. Luego de controlar por las características observables, la brecha aumenta a 24.2% en el empleo formal y a 20.7% en el informal.
II. Metodología
1. La descomposición de Blinder-Oaxaca y sus extensiones
La descomposición de Blinder-Oaxaca clásica (B-O de ahora en adelante), propuesta originalmente por Blinder (1973) y Oaxaca (1973), descompone la diferencia de la media aritmética del logaritmo de los salarios en dos grupos, en este caso: hombres y mujeres.
Esta descomposición utiliza una regresión semilogarítmica separada en ambos grupos:
donde s∈ {H, M} (hombre o mujer, respectivamente), wsi es el salario de la persona i en el grupo s, X es el vector de los distintos controles (educación, experiencia laboral, etc.), y βs es el vector de coeficientes del grupo s. Como es costumbre, asumimos E(μsi | Xsi) = 0, con una varianza σsμ. Dado esto, podemos obtener la regresión muestral:
Finalmente, la brecha salarial se puede expresar como:
Una simple operación matemática aplicada en el lado derecho de la ecuación (3)1 nos lleva a la descomposición de Oaxaca-Blinder:
Podemos explicar esta ecuación de la siguiente forma:
donde el término del lado izquierdo es la diferencia total en el salario que surge de las diferentes características y los rendimientos por estas características que recibe cada grupo.2
En este modelo: 1) la parte explicada, el primer término del lado derecho de la ecuación (5), representa la diferencia en el logaritmo de los salarios que se debe a los diferentes niveles de características de ambos grupos; 2) la parte no explicada, el segundo término del lado derecho de la ecuación (5), se debe a la diferencia en los coeficientes y se asocia con discriminación, ya que conduce a una diferencia salarial entre ambos grupos, incluso si ambos poseen exactamente las mismas características en promedio (Deshpande et al., 2018).
Después de la descomposición B-O, Masters (1974) mostró una extensión de ésta; nuevamente partiendo de la ecuación (3)3 se puede llegar a su descomposición:4
donde un signo positivo en el coeficiente de interacción indica que los retornos de los hombres tienden a ser mayores para aquellas características para las cuales éstos tienen medias más altas, y viceversa.
Volviendo al modelo general de la descomposición B-O, expresado en la ecuación (5), podemos generalizarlo de la siguiente manera:
donde β* es el vector de coeficientes estimado para una estructura salarial libre de discriminación, es decir, que incluye a hombres y mujeres:
expresión en la cual I representa la matriz identidad, y Ω, una matriz diagonal de ponderaciones. Es fácil notar que en el modelo B-O inicial Ω = I, y así el primer término del lado derecho de la ecuación (7) desaparece (o en su símil, cuando Ω =0, desaparece el segundo término del lado derecho de la ecuación [7]).
El modelo de Reimers (1983) usa Ω =0.5, mientras que el modelo de Cotton (1988) elige Ω = cI, donde c denota el tamaño relativo en la muestra del grupo mayoritario. Posteriormente, Neumark (1988) y Oaxaca y Ransom (1994) asumen que la estructura salarial en ausencia de discriminación corresponde a los coeficientes estimados con la muestra completa, es decir, obtienen β * de la estimación en la muestra con hombres y mujeres. En estos últimos modelos no se elimina ningún término en la ecuación (7).
Podemos interpretar el lado derecho de la ecuación (7) de la siguiente manera: 1) el primer término del lado derecho corresponde al sobrepago salarial de los hombres: favoritismo; 2) el segundo término representa el subpago salarial de las mujeres: discriminación pura; 3) finalmente, el último término denota las diferencias en características, también llamadas diferencias de dotación o productividad (Oaxaca y Ransom, 1994).
2. Corrección por sesgo de selección
A pesar de la evolución que ha tenido la descomposición B-O en el tiempo, ésta no es ajena a problemas econométricos. Al estimar cualquier ecuación de salarios se está incurriendo en un sesgo de selección, ya que la muestra utilizada, debido a su naturaleza, se encuentra únicamente construida con personas que están trabajando en el momento de la recolección de datos.
La solución para este problema fue dada por Heckman (1977) y consiste en estimar un modelo probit previo para calcular la probabilidad de estar trabajando; luego de dicha estimación se calcula la inversa del ratio de Mills, la cual se incluye en la regresión de salarios original. Esta corrección es incluida por Reimers (1983) y Oaxaca y Ransom (1994).5
Se estima un modelo de probabilidad de participación laboral separado por grupo:
Donde
Finalmente, y al igual que usi, E(εsi | Hsi) = 0, con una varianza σsε.
Con esto:
donde θs = ρs °σsμ, con ρs la covarianza entre σsμ y σsε, y λsi, la inversa del ratio de Mills, que se define de la siguiente manera:
donde ϕ (∙) es la función de densidad normal estándar y Φ(∙), la función de distribución acumulada normal estándar.
Finalmente, se llega a la descomposición de la brecha salarial:
donde el último término del lado derecho de la ecuación (12) corresponde a la corrección que se debe hacer por la presencia de sesgo de selección.
3. Método de descomposición por cuantiles
Las metodologías de regresión por cuantil (QR de ahora en adelante) son otro tipo extensión de la descomposición B-O clásica, en este caso aplicada a los distintos cuantiles de ingreso. En este trabajo se usa el refinamiento que hace Melly (2006) a la metodología de Machado y Mata (2005) (MMM de ahora en adelante).6
La metodología QR supone que la variable dependiente (logaritmo de los salarios) del cuantil α es lineal en las variables X. Entonces, la distribución condicional del cuantil α viene dada por:
donde el estimador de βsα se obtiene mediante el siguiente problema:
donde:
Las regresiones por cuantil nos permiten estimar, al igual que la descomposición B-O, el efecto marginal de las variables que afectan al salario, pero en este caso, por cada cuantil de ingreso.
Finalmente, tenemos la descomposición de los salarios similar a la descomposición B-O, pero esta vez para cada cuantil de ingreso:
Donde
Es importante hacer notar que esta metodología se basa en la descomposición B-O original, y no en sus versiones más detalladas. Además, este método no corrige por sesgo de selección mostrado en la sección anterior. Como solución a este problema, con base en Buchinsky (2001), se ha agregado la inversa del ratio de Mills al vector X previamente calculado con el modelo de probabilidad de participación laboral. Esto es una aproximación a la corrección por sesgo de selección propuesta por Heckman (1977).
III. Datos y estadísticas descriptivas
En este trabajo se han utilizado datos chilenos de la encuesta Casen, desde 1990 hasta 2017, con intervalos de dos o tres años entre cada encuesta.7 La Casen provee, entre mucha otra información relevante para otras áreas, datos de ingresos totales, ingresos autónomos e ingresos por el trabajo principal de los individuos, así como las horas trabajadas en dicho empleo, educación, estado civil, género, etc. Nosotros usaremos los ingresos por hora únicamente de la ocupación principal, y el logaritmo de éstos, así como datos de educación, edad, género, entre otros controles.8
Como una manera de trabajar con una población homogénea, se decidió incluir solamente a hombres de entre 18 y 64 años de edad y mujeres de entre 18 y 59 años,9 trabajadores dependientes que se encuentran en la categoría de empleados y obreros públicos o privados con jornada completa.10 Además, se considera a las personas en dicho rango de edad que están sin empleo para corregir por sesgo de selección.
Para la experiencia laboral, ésta se ha conformado de la manera usual, es decir, la experiencia laboral de una persona se construye como la experiencia laboral potencial: la edad de la persona, menos los años de educación, menos seis.11 Heckman (1977) propone restarle a esta variable una unidad por cada hijo para el caso de las mujeres. A pesar de estar de acuerdo con este criterio, no se ha procedido de esta manera en el presente trabajo debido a que no se tiene información de los hijos para todos los años de la base de datos.
Otros trabajos critican abiertamente el supuesto de usar la experiencia laboral potencial, ya que diverge mucho de la experiencia laboral efectiva, sobre todo en grupos afectados por discriminación: afrodescendientes, mujeres, inmigrantes, etc. Esto se debe a que la experiencia laboral, como factor limitante y discriminatorio, está muy condicionada a las interrupciones que tienen las mujeres en su vida laboral (Perticará y Astudillo, 2010). En Chile la única fuente de información capaz de calcular una experiencia laboral efectiva con mayor certeza es la Encuesta de Protección Social, pero con una muestra mucho menor a la de la Casen, y solamente disponible de 2002 a 2015.
Por último, los ingresos de la ocupación principal por hora trabajada (que de ahora en adelante llamaremos salarios por hora) se han pasado a pesos chilenos de 2017 mediante datos del Índice de Precios al Consumidor (IPC) de Chile, y también se ocupa la Tasa de Desempleo Regional de cada año.12 En el Cuadro 1 se muestran estadísticas descriptivas de las variables más relevantes en este estudio y las usadas posteriormente en las estimaciones para 2017 por género y por situación de empleo, además de la brecha porcentual entre hombres y mujeres.13
Cuadro 1 Estadísticas descriptivas de variables relevantes, 2017a
| Con empleo | Sin empleo | |||||
|---|---|---|---|---|---|---|
| Mujeres | Hombres | Brecha % | Mujeres | Hombres | Brecha % | |
| Años de educación | 13.4 | 12.2 | -8.9 | 11.6 | 12.1 | 4.3 |
| Experiencia laboral | 18.8 | 22.1 | 17.3 | 18.7 | 14 | -25 |
| Salario por hora | $2 940 | $3 229 | 9.8 | |||
| Soltero | 39.3% | 30.8% | -21.7 | 40.6% | 74.4% | 83.2 |
| Casado | 25.3% | 38.1% | 50.7 | 33.8% | 13.2% | -61.1 |
| Zona sur | 31.7% | 33.9% | 6.8 | 39% | 37.5% | -3.9 |
| Zona norte | 20.2% | 21.2% | 4.9 | 24.9% | 24.6% | -1.1 |
| Zona rural | 8% | 11.7% | 46.3 | 15% | 11.3% | -24.2 |
| Niños menores de 6 años | 0.3 | 0.3 | -3 | 0.4 | 0.2 | -57.5 |
| Niños menores de 18 años | 0.6 | 0.6 | -10.9 | 0.7 | 0.5 | -31 |
| Jefe de hogar | 36.3% | 55.5% | 52.7 | 16.3% | 18.8% | 15.3 |
| Ingreso familiar per cápita | $246 259 | $187 931 | -23.7 | $224 918 | $238 678 | 6.1 |
a Salarios por hora en pesos chilenos de 2017. Niños menores de 18 años son también mayores de seis años. El ingreso familiar per cápita no considera el ingreso de la persona en caso de estar trabajando, medido en pesos chilenos de 2017.
Fuente: elaboración propia con base en datos de la Casen.
El Cuadro 1 muestra, para 2017, una gran brecha en favor de las mujeres en cuanto a años de educación para la población empleada, pero esta brecha casi desaparece en la población sin trabajo. Por otro lado, los hombres presentan una gran ventaja en variables relevantes como los años de experiencia laboral, los salarios y la condición de ser jefe de hogar.
Finalmente, se presentan estadísticas descriptivas de las variables más relevantes en este estudio a lo largo del periodo estudiado: la participación laboral, los salarios por hora, el nivel de educación y el nivel de experiencia laboral.
1. Participación en la fuerza laboral
En la Gráfica 1 se puede observar la evolución de la participación laboral por género y la brecha que deja ésta. Si bien la brecha ha disminuido considerablemente situándose en una tercera parte de lo que era hasta hace 27 años, aún la cifra es alta: llegó a 55% en 2017.14

Fuente: elaboración propia con base en datos de la Casen.
Gráfica 1 Evolución de la participación laboral, 1990-2017
Entre 1990 y 2017 la tasa de participación laboral de las mujeres ha aumentado dramáticamente: de 30.4% en 1990 a 48% en 2017. Mientras tanto, la de los hombres ha tenido una leve caída en dicho periodo: de 76.2% en 1990 a 74.7% en 2017, como muestra la Gráfica 1a.
Si calculamos la brecha en la participación laboral, en todos los años está en favor de los hombres, pero ha caído drásticamente en los últimos: de 150.8% en 1990 a 55.7% en 2017, como se observa en la Gráfica 1b.15
Según el estudio de la Comisión Económica para América Latina y el Caribe (CEPAL, 2019), la participación laboral en personas de 15 años o más representó una brecha de 25.9 puntos porcentuales (pp) en promedio en América Latina en favor de los hombres (equivalente a una brecha de 49.9%) en 2018. En América Latina y el Caribe esta brecha es liderada por Guatemala (45 pp), México (34 pp) y Honduras (33.3 pp), mientras que Chile apenas supera 20 pp, pero aún está lejos de los últimos lugares en este ámbito (Perú, Uruguay y Bolivia, con valores en torno a 15 pp).
2. Salarios por hora
En la Gráfica 2 se observan la evolución en los salarios por hora por género y la brecha de ésta. Se muestra que, si bien ambos salarios han crecido en el tiempo, el de los hombres, en promedio, siempre ha estado sobre el de las mujeres.16

Fuente: elaboración propia con base en datos de la Casen.
Gráfica 2 Evolución de los salarios por hora, en pesos chilenos de 2017 (1990-2017)
Entre 1990 y 2017 los salarios por hora de hombres y mujeres han aumentado considerablemente. En el caso de las mujeres éstos pasaron de $1 270 en 1990 a $2 940 en 2017. Por otro lado, para los hombres aumentaron de $1 459 en 1990 a $3 229 en 2017, como muestra la Gráfica 2a.
La Gráfica 2b demuestra que la brecha salarial entre hombres y mujeres es bastante variable: entre 6 y 16% de 1990 a 2017, cuando alcanza un valor de 9.8 por ciento.
3. Años de educación y de experiencia laboral
Finalmente, en la Gráfica 3 se muestra la evolución de las dos variables más relevantes cuando se estima una ecuación de salarios estilo Mincer (1974): los años de educación y los años de experiencia laboral.17
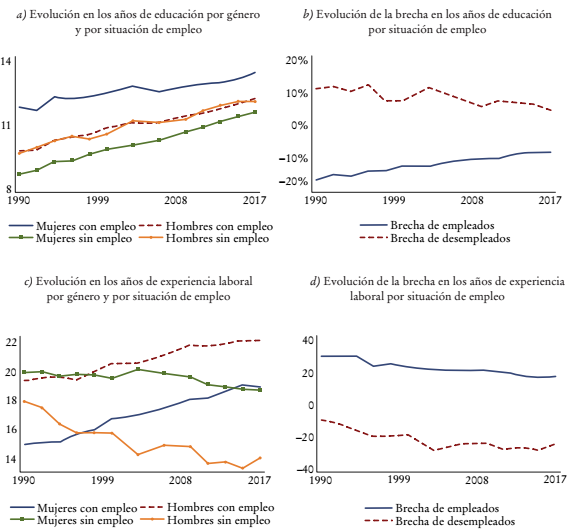
Fuente: elaboración propia con base en datos de la Casen.
Gráfica 3 Evolución de los años de educación y los años de experiencia laboral, 1990-2017
En la Gráfica 3a se muestra la evolución de los años de educación por género y por situación de empleo, cuando se observa un aumento sostenido tanto para hombres como para mujeres con y sin empleo. Sin embargo, quizá lo más relevante es que para todo el periodo entre 1990 y 2017 las mujeres empleadas, en promedio, presentan más años de educación que los hombres desempleados y empleados, lo cual va en contra de la teoría de Mincer, considerando que los hombres obtienen un mayor salario que las mujeres, como se mostró en el Cuadro 1.
Además, se observa que no hay diferencias significativas en hombres empleados y desempleados salvo en los últimos años. Si bien la brecha por género en años educación, para personas tanto empleadas como desempleadas, ha disminuido en las últimas décadas -como se muestra en la Gráfica 3b-, aún en 2017 se observa que los hombres con empleo tienen estudios inferiores a las mujeres con empleo en 8.9%, mientras que los hombres desempleados tienen estudios superiores a las mujeres desempleadas en 4.3 por ciento.
Por otro lado, en la Gráfica 3c se muestra la evolución de los años de experiencia laboral potencial por género y por situación de empleo: se observa un ligero aumento en el tiempo de la experiencia de las personas empleadas, y una leve disminución de las personas desempleadas hasta 2017. Finalmente, en la Gráfica 3d se muestra que los hombres empleados tienen entre 20 y 30% más experiencia laboral que las mujeres empleadas. En cambio, los hombres desempleados tienen entre 10 y 30% menos experiencia laboral que las mujeres desempleadas hasta 2017.
IV. Resultados
En esta sección se muestran los resultados de las principales estimaciones de las metodologías de descomposición de la brecha salarial propuestas en la sección II. Además, se mostrarán los resultados de estimaciones de la probabilidad de observar salarios positivos (probabilidad de estar trabajando) y estimaciones de salarios, con y sin corrección por sesgo de selección para 2017. Luego, se mostrarán los resultados de las estimaciones de descomposición para todo el periodo entre 1990 y 2017, con el fin de observar la evolución de la brecha salarial y la posible discriminación en Chile. Finalmente, se presentarán los resultados de las descomposiciones por cuantil.
1. Modelo probit
En este apartado, específicamente en el Cuadro 2, se muestran los resultados de la estimación de probabilidad de estar trabajando para 2017.18
Cuadro 2 Estimación de probabilidad de observar salarios positivos, 2017a
| Variables | (1) | (2) | (3) |
|---|---|---|---|
| Hombres | Mujeres | Muestra completa | |
| Ingreso familiar per cápita | -0.01*** | -0.01*** | -0.01*** |
| (0.00) | (0.00) | (0.00) | |
| Niños menores de 6 años | 0.12*** | -0.08*** | -0.02* |
| (0.02) | (0.02) | (0.01) | |
| Niños menores de 18 años | -0.05*** | -0.08*** | -0.08*** |
| (0.01) | (0.01) | (0.01) | |
| Jefe de hogar | 0.48*** | 0.53*** | 0.82*** |
| (0.03) | (0.03) | (0.02) | |
| Divorciado | -0.32*** | 0.18*** | -0.19*** |
| (0.04) | (0.03) | (0.02) | |
| Soltero | -0.65*** | 0.20*** | -0.09*** |
| (0.03) | (0.03) | (0.02) | |
| Desempleo regional | -4.29*** | -5.58*** | -4.43*** |
| (0.84) | (0.73) | (0.53) | |
| Años de educación | 0.02*** | 0.10*** | 0.06*** |
| (0.00) | (0.00) | (0.00) | |
| Años de experiencia | 0.10*** | 0.10*** | 0.08*** |
| (0.00) | (0.00) | (0.00) | |
| Años de experiencia2 | -0.20*** | -0.21*** | -0.15*** |
| (0.01) | (0.01) | (0.00) | |
| Zona rural | 0.12*** | -0.12*** | -0.02 |
| (0.03) | (0.03) | (0.02) | |
| Zona norte | -0.20*** | -0.26*** | -0.24*** |
| (0.03) | (0.03) | (0.02) | |
| Zona sur | -0.22*** | -0.24*** | -0.24*** |
| (0.03) | (0.03) | (0.02) | |
| Constante | 0.26*** | -1.77*** | -0.80*** |
| (0.09) | (0.08) | (0.06) | |
| Observaciones | 44 856 | 47 208 | 92 064 |
aNiños menores de 18 años son también mayores de seis años. El ingreso familiar per cápita no considera el ingreso de la persona en caso de estar trabajando, medido en cientos de miles de pesos chilenos de 2017. Errores estándar robustos en paréntesis: ***p < 0.01, **p < 0.05, *p < 0.1.
Fuente: elaboración propia con base en datos de la Casen.
Como se muestra en el Cuadro 2, los signos de los coeficientes se mantienen en la mayoría de las variables cuando observamos las estimaciones separadas por hombres, mujeres y la muestra completa. Los resultados más interesantes muestran que un año más de educación beneficia mucho más a las mujeres que a los hombres en la posibilidad de tener un empleo. De la misma manera, el desempleo regional afecta mucho más a las mujeres que a los hombres, al igual que pertenecer a la zona sur o la zona norte del país.19 También tener niños pequeños en el hogar afecta negativamente a la mujer, mientras que el hombre trabaja más cuando hay niños presentes. Por último, ser divorciada o soltera afecta positivamente a las mujeres y negativamente a los hombres en las posibilidades de estar trabajando.20
2. Regresiones de salarios
En este apartado se muestran los resultados de las estimaciones de salarios para 2017; se distingue entre mujeres y hombres, y, al mismo tiempo, se comparan la estimación sin corrección por sesgo de selección y la estimación cuando se corrige por este método con la metodología propuesta en la sección II para 2017.21
Como muestran los Cuadros 3 y 4, no hay gran variación en los signos ni en la magnitud de los coeficientes cuando observamos a mujeres y hombres, e incluso cuando observamos regresiones sin la inversa del ratio de Mills y luego agregando esta variable.
Cuadro 3 Estimación de salarios sin corrección por sesgo de selección, 2017a
| Variables | (1) | (2) | (3) |
|---|---|---|---|
| Hombres | Mujeres | Muestra completa | |
| Desempleo regional | -1.30*** | -1.90*** | -1.37*** |
| (0.43) | (0.45) | (0.39) | |
| Años de educación | 0.11*** | 0.13*** | 0.12*** |
| (0.00) | (0.00) | (0.00) | |
| Experiencia laboral | 0.02*** | 0.01*** | 0.02*** |
| (0.00) | (0.00) | (0.00) | |
| Experiencia laboral2 | -0.02*** | -0.01*** | -0.01*** |
| (0.00) | (0.00) | (0.00) | |
| Zona rural | -0.01 | -0.00 | 0.00 |
| (0.01) | (0.02) | (0.01) | |
| Zona norte | -0.08*** | -0.12*** | -0.09*** |
| (0.01) | (0.02) | (0.01) | |
| Zona sur | -0.14*** | -0.16*** | -0.14*** |
| (0.01) | (0.02) | (0.01) | |
| Constante | 6.25*** | 6.05*** | 6.21*** |
| (0.05) | (0.05) | (0.04) | |
| Observaciones | 31 134 | 19 166 | 50 300 |
| R-squared | 0.36 | 0.38 | 0.35 |
a Al ser un modelo semilogarítmico, el efecto marginal del coeficiente será exp(β) - 1. Errores estándar en paréntesis: ***p < 0.01, **p < 0.05, *p < 0.1.
Fuente: elaboración propia con base en datos de la Casen.
Cuadro 4 Estimación de salarios con corrección por sesgo de selección, 2017a
| Variables | (1) | (2) | (3) |
|---|---|---|---|
| Hombres | Mujeres | Muestra completa | |
| Desempleo regional | -0.84* | -2.48*** | -0.91** |
| (0.43) | (0.46) | (0.39) | |
| Años de educación | 0.11*** | 0.14*** | 0.11*** |
| (0.00) | (0.00) | (0.00) | |
| Experiencia laboral | 0.00 | 0.03*** | 0.00 |
| (0.00) | (0.00) | (0.00) | |
| Experiencia laboral2 | 0.02*** | -0.04*** | 0.02*** |
| (0.00) | (0.01) | (0.00) | |
| Zona rural | -0.03** | -0.03* | -0.00 |
| (0.01) | (0.02) | (0.01) | |
| Zona norte | -0.05*** | -0.14*** | -0.07*** |
| (0.01) | (0.02) | (0.01) | |
| Zona sur | -0.11*** | -0.18*** | -0.12*** |
| (0.01) | (0.02) | (0.01) | |
| Mills | -0.35*** | 0.18*** | -0.28*** |
| (0.02) | (0.03) | (0.01) | |
| Constante | 6.60*** | 5.72*** | 6.55*** |
| (0.05) | (0.08) | (0.04) | |
| Observaciones | 31 134 | 19 166 | 50 300 |
| R-squared | 0.37 | 0.38 | 0.36 |
a Mills es la inversa del ratio de Mills. Al ser un modelo semilogarítmico, el efecto marginal del coeficiente será exp(β) - 1. Errores estándar en paréntesis: ***p < 0.01, **p < 0.05, *p < 0.1.
Fuente: elaboración propia con base en datos de la Casen.
La mayor diferencia se observa en las variables binarias de zona norte y zona sur del país, donde, para 2017, al añadir la inversa del ratio de Mills, pertenecer a la zona norte reduce, en promedio, el salario de los hombres en 4.9% y el de las mujeres en 13.1%. En la zona sur se reduce el salario de los hombres en 11.6% y el de las mujeres en 19.7 por ciento.
3. Descomposiciones
En esta sección se muestran los resultados de las descomposiciones de brecha salarial para 2017 mediante las cuatro metodologías propuestas con base en Blinder (1973) y Oaxaca (1973): 1) descomposición de Masters (1974), 2) descomposición de Reimers (1983), 3) descomposición de Cotton (1988) y 4) descomposición de Oaxaca y Ransom (1994). En todos los casos se ha estimado sin corrección por error de selección y corrigiendo por este problema.22
Como muestran los Cuadros 5 y 6, el logaritmo natural de los salarios por hora promedio de los hombres alcanza 7.81 (2 465 pesos chilenos de 2017), mientras que el de las mujeres solamente llega a 7.75 (2 327 pesos chilenos de 2017) para 2017. Esto genera una brecha de 5.9%, pero en el momento de corregir por sesgo de selección, se observa que la diferencia ajustada alcanza 37.7 por ciento.
Cuadro 5 Estimación de descomposiciones sin corrección por sesgo de selección, 2017a
| Variables | (1) | (2) | (3) | (4) |
|---|---|---|---|---|
| Masters (1974) | Reimers (1983) | Cotton (1988) | Oaxaca y Ransom (1994) | |
| Predicción hombres | 7.81*** | 7.81*** | 7.81*** | 7.81*** |
| (0.01) | (0.01) | (0.01) | (0.01) | |
| Predicción mujeres | 7.75*** | 7.75*** | 7.75*** | 7.75*** |
| (0.01) | (0.01) | (0.01) | (0.01) | |
| Diferencia | 0.06*** | 0.06*** | 0.06*** | 0.06*** |
| (0.01) | (0.01) | (0.01) | (0.01) | |
| Dotaciones | -0.13*** | |||
| (0.01) | ||||
| Coeficientes | 0.16*** | |||
| (0.01) | ||||
| Interacción | 0.02*** | |||
| (0.00) | ||||
| Productividad | -0.12*** | -0.11*** | -0.11*** | |
| (0.01) | (0.01) | (0.01) | ||
| Favoritismo | 0.09*** | 0.07*** | 0.06*** | |
| (0.00) | (0.00) | (0.00) | ||
| Discriminación pura | 0.08*** | 0.10*** | 0.10*** | |
| (0.00) | (0.00) | (0.00) | ||
| Observaciones | 50300 | 50300 | 50300 | 50300 |
a Al ser un modelo con variable dependiente logarítmica, los coeficientes deben ser transformados usando la función exponencial para obtener los salarios reales y las brechas porcentuales. Errores estándar en paréntesis: ***p < 0.01, **p < 0.05, *p < 0.1.
Fuente: elaboración propia con base en datos de la Casen.
Cuadro 6 Estimación de descomposiciones con corrección por sesgo de selección, 2017a
| Variables | (1) | (2) | (3) | (4) |
|---|---|---|---|---|
| Masters (1974) | Reimers (1983) | Cotton (1988) | Oaxaca y Ransom (1994) | |
| Predicción hombres | 7.81*** | 7.81*** | 7.81*** | 7.81*** |
| (0.01) | (0.01) | (0.01) | (0.01) | |
| Predicción mujeres | 7.75*** | 7.75*** | 7.75*** | 7.75*** |
| (0.01) | (0.01) | (0.01) | (0.01) | |
| Diferencia | 0.06*** | 0.06*** | 0.06*** | 0.06*** |
| (0.01) | (0.01) | (0.01) | (0.01) | |
| Diferencia ajustada | 0.32*** | 0.32*** | 0.32*** | 0.32*** |
| (0.03) | (0.03) | (0.03) | (0.03) | |
| Dotaciones | -0.15*** | |||
| (0.01) | ||||
| Coeficientes | 0.42*** | |||
| (0.03) | ||||
| Interacción | 0.05*** | |||
| (0.01) | ||||
| Productividad | -0.12*** | -0.12*** | -0.10*** | |
| (0.01) | (0.01) | (0.00) | ||
| Favoritismo | 0.23*** | 0.18*** | 0.04*** | |
| (0.01) | (0.01) | (0.01) | ||
| Discriminación pura | 0.21*** | 0.26*** | 0.37*** | |
| (0.01) | (0.02) | (0.02) | ||
| Observaciones | 50300 | 50300 | 50300 | 50300 |
a Al ser un modelo con variable dependiente logarítmica, los coeficientes deben ser transformados con la función exponencial para obtener los salarios reales y las brechas porcentuales. Errores estándar en paréntesis: ***p < 0.01, **p < 0.05, *p < 0.1.
Fuente: elaboración propia con base en datos de la Casen.
En todos los modelos se observa que el coeficiente asociado con conocimientos (también llamado productividad y dotaciones) tiene signo negativo de aproximadamente -10%. Es decir, al tener las mujeres mejores características (por ejemplo, mayor educación), la brecha salarial se ve disminuida.
Esto implica que si las mujeres tuvieran las mismas características que los hombres (mismo nivel educativo, por ejemplo), recibirían un salario aún menor al que reciben actualmente.
Por otro lado, en el modelo de Masters (1974) se puede observar que el efecto de la interacción es bastante bajo en comparación con el efecto de los coeficientes (que puede ser leído como la discriminación salarial en este modelo). Además, se observa que, al no corregir por sesgo de selección, se subestima la discriminación salarial, debido a que se subestima la diferencia de ambos grupos. Cuando no se corrige por sesgo de selección, se observa que la discriminación alcanza 17.7%, mientras que, al corregir por sesgo de selección, llega a 52% para 2017.
Finalmente, en el resto de los modelos se observa que tanto el favoritismo como la discriminación pura se subestiman al no corregir por sesgo de selección, y que ambos juntos pueden explicar la discriminación salarial. Según el modelo de Oaxaca y Ransom (1994), al corregir por sesgo de selección, la discriminación alcanzó 49.7% en 2017, cuando 45.2% correspondió a la discriminación pura en contra de la mujer y 4.5% al favoritismo en favor del hombre. Por otro lado, cuando no se corrige por sesgo de selección, la discriminación alcanzó 17.1% en 2017, cuando 10.5% correspondió a la discriminación pura y 6.6% al favoritismo de los hombres, lo cual muestra que la discriminación se subestima si no se corrige por sesgo de selección.
4. Resultados para todo el periodo de 1990 a 2017
En este apartado se muestran los resultados de las descomposiciones de brecha salarial para la totalidad del periodo estudiado mediante las cuatro metodologías propuestas, como en la sección anterior. En todos los casos se ha realizado la estimación sin y con corrección por sesgo de selección. En la Gráfica 4 se muestran los resultados sin corrección por sesgo de selección, mientras que en la Gráfica 6 sí se corrige por este problema.23

Fuente: elaboración propia con base en datos de la Casen.
Gráfica 4 Evolución de la estimación de los componentes de la brecha salarial sin corrección por sesgo de selección, 1990-2017
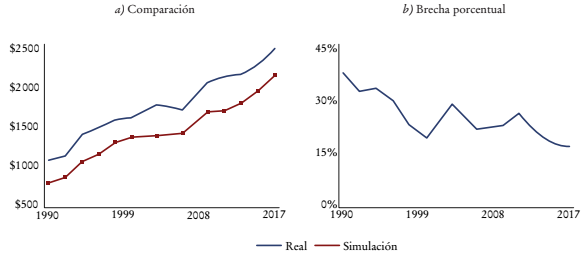
Fuente: elaboración propia con base en datos de la Casen.
Gráfica 5 Estimación del salario por hora de las mujeres con una simulación con las características observables de los hombres, 1990-2017 (en pesos chilenos de 2017)

Fuente: elaboración propia con base en datos de la Casen.
Gráfica 6 Evolución de la estimación de los componentes de la brecha salarial al corregir por sesgo de selección, 1990-2017
Como se muestra en todos los modelos sin corrección por sesgo de selección, en la Gráfica 4 la brecha ocasionada por las características o la productividad siempre es negativa, es decir, tener mejores características ayuda a la mujer a disminuir la brecha existente en los salarios. Si ambos grupos tuvieran las mismas características, la brecha salarial subiría entre 10 y 20 puntos porcentuales a lo largo del periodo estudiado.
Como se comentó en el punto anterior, esto implica que, si las mujeres tuvieran las mismas características que los hombres, recibirían un salario aún menor al que obtienen actualmente, lo cual se puede constatar en la Gráfica 5, donde se simula el salario que tendrían las mujeres si tuviesen las características de los hombres
Según el modelo Masters (1974), el efecto de la interacción es bastante bajo en comparación con el de los coeficientes (discriminación), el cual bordea 20% en el periodo estudiado.
Finalmente, en el resto de los modelos mostrados, en los paneles 4b, 4c y 4d, si no se corrige por sesgo de selección, se observa cierta estabilidad en el favoritismo y la discriminación pura, aunque hay un ligero aumento en el favoritismo de los hombres -5.1% en 1990 y 6.6% en 2017 con base en el modelo de Oaxaca y Ransom (1994)- y una caída en la discriminación pura hacia las mujeres -14% en 1990 y 10.5% en 2017 con base en el modelo de Oaxaca y Ransom (1994)-.
Por otro lado, en el momento de corregir por sesgo de selección, como se muestra en la Gráfica 6, la primera conclusión importante es que la estimación sin corrección por sesgo de selección subestima la discriminación salarial. En todos los modelos, al igual que en los casos anteriores, la brecha ocasionada por las características o la productividad siempre es negativa y estable entre 10 y 20%, a lo largo del periodo. Sin embargo, es importante mencionar que ha tenido un leve aumento en el tiempo -con -15.4% en 1990 y -9.2% en 2017 con base en el modelo de Oaxaca y Ransom (1994)-, lo cual favorece a las mujeres, ya que este componente hace disminuir la brecha salarial. Esto ocurre debido a que las mujeres tienen mejores características laborales que los hombres, como ya se ha mostrado.
Finalmente, se observa que en todos los modelos la discriminación salarial ha venido disminuyendo desde 1990, pero es desde principios de los años 2000 que esta caída está estancada.
5. Discriminación salarial por variable
En este apartado se muestra el detalle de las variables involucradas en los resultados de la descomposición según el modelo de Oaxaca y Ransom (1994) al corregir por sesgo de selección.
Como se muestra en el Cuadro 7, en la descomposición para 2017 se muestra que la mayor diferencia en productividad (características) está en la variable educación, la cual llega a 12% en favor de las mujeres.
Cuadro 7 Descomposición de Oaxaca y Ransom (1994) por variable, 2017a
| Coeficiente | Valor p | Intervalo de confianza (95%) | ||
|---|---|---|---|---|
| General | ||||
| Predicción de hombres | $2465.13 | 0 | $2426.62 | $2504.24 |
| Predicción de mujeres | $2327.29 | 0 | $2281.15 | $2374.35 |
| Diferencia | 1.06 | 0 | 1.04 | 1.08 |
| Diferencia ajustada | 1.38 | 0 | 1.31 | 1.45 |
| Productividad | ||||
| Desempleo regional | -0.01 | 0.22 | -0.03 | 0.01 |
| Años de educación | -11.99 | 0 | -1.87 | -11.11 |
| Experiencia laboral | 0.52 | 0.20 | -0.27 | 1.31 |
| Experiencia laboral2 | 2.95 | 0 | 2.05 | 3.85 |
| Zona rural | -0.01 | 0.77 | -0.10 | 0.08 |
| Zona norte | -0.06 | 0.02 | -0.12 | -0.01 |
| Zona sur | -0.25 | 0 | -0.37 | -0.13 |
| Total | -9.24 | 0 | -10.08 | -8.40 |
| Favoritismo | ||||
| Desempleo regional | 0.52 | 0.64 | -1.65 | 2.73 |
| Años de educación | 0.35 | 0.76 | -1.90 | 2.66 |
| Experiencia laboral | -2.86 | 0.35 | -8.62 | 3.26 |
| Experiencia laboral2 | 1.37 | 0.45 | -2.11 | 4.96 |
| Zona rural | -0.28 | 0 | -0.41 | -0.15 |
| Zona norte | 0.28 | 0.08 | -0.03 | 0.59 |
| Zona sur | 0.27 | 0.26 | -0.19 | 0.72 |
| Constante | 4.96 | 0.05 | -0.08 | 10.27 |
| Total | 4.53 | 0 | 3.19 | 5.88 |
| Discriminación pura | ||||
| Desempleo regional | 10.97 | 0 | 6.76 | 15.35 |
| Años de educación | -32.58 | 0 | -36.71 | -28.17 |
| Experiencia laboral | -37 | 0 | -42.71 | -30.71 |
| Experiencia laboral2 | 28.69 | 0 | 21.73 | 36.05 |
| Zona rural | 0.20 | 0.04 | 0.01 | 0.39 |
| Zona norte | 1.59 | 0 | 1.15 | 2.04 |
| Zona sur | 2 | 0 | 1.38 | 2.62 |
| Constante | 130.47 | 0 | 102.85 | 161.86 |
| Total | 45.17 | 0 | 38.63 | 52.02 |
a Los coeficientes mostrados ya están transformados mediante la función exponencial. Salarios por hora en pesos chilenos de 2017.
Fuente: elaboración propia con base en datos de la Casen.
En el caso de la discriminación, el favoritismo hacia los hombres se debe principalmente a la experiencia laboral, mientras que la discriminación pura hacia la mujer se debe principalmente a la variable experiencia laboral y al desempleo regional.
Por otro lado, en el Cuadro 8 se muestra la parte de la discriminación salarial asociada con la discriminación pura según el modelo de Oaxaca y Ransom (1994) por variable y por año para todo el periodo estudiado. Se observa que en la totalidad del periodo el mayor componente de la discriminación es la experiencia laboral; además, en los últimos años también el desempleo regional se ha convertido en una variable importante de este componente. Finalmente, es importante mencionar que las variables binarias por zona también aumentan la discriminación salarial, aunque mucho menos que otras variables.
Cuadro 8 Discriminación pura hacia la mujer según el modelo de Oaxaca y Ransoma
| Desem. | Educación | Exper. | Exper.2 | Rural | Norte | Sur | Const. | Total | |
|---|---|---|---|---|---|---|---|---|---|
| 1990 | -5.54 | -29.08 | -17.95 | 13.63 | -0.24 | 2.68 | 2.66 | 171.58 | 78.38 |
| 1992 | -3.76 | -19.49 | -16.12 | 13.75 | -0.29 | 2.64 | 1.35 | 114.23 | 64.25 |
| 1994 | 6.35 | -23.30 | -8.89 | 7.58 | -0.20 | 1.73 | 1.10 | 83.96 | 50.97 |
| 1996 | -15.26 | -15.26 | -14.33 | 8.40 | -0.46 | 1.75 | -0.10 | 179.66 | 57.60 |
| 1998 | -9.77 | -31.14 | -19.14 | 11.56 | -0.14 | 1.77 | 1.02 | 170.17 | 55.48 |
| 2000 | -5.77 | -31.16 | -14.05 | 9.34 | 0.11 | 1.50 | -0.50 | 146.63 | 52 |
| 2003 | -3.45 | -37.11 | -18.35 | 11.34 | 0.11 | 1.83 | 1.45 | 161.84 | 49.48 |
| 2006 | -2.24 | -35.13 | -24.79 | 16.36 | -0.26 | 1.73 | 1.58 | 167.08 | 52.79 |
| 2009 | -0.91 | -31.85 | -34.32 | 26.69 | -0.18 | 2.61 | 1.75 | 171.43 | 58.93 |
| 2011 | 10.86 | -37.44 | -39.00 | -39.00 | 0.02 | 2.02 | 2.21 | 179.55 | 61.80 |
| 2013 | 15.29 | -36.39 | -42.04 | 35.22 | 0.11 | 1.63 | 2.07 | 171.84 | 62.23 |
| 2015 | 13.27 | -34.05 | -39.45 | 31.62 | 0.20 | 1.81 | 1.81 | 145.27 | 51.87 |
| 2017 | 10.97 | -32.58 | -37.00 | 28.69 | 0.20 | 1.59 | 2 | 130.47 | 45.17 |
aLos coeficientes mostrados de las descomposiciones ya están transformados mediante la función exponencial. Desem. es desempleo regional.
Fuente: elaboración propia con base en datos de la Casen.
6. Discriminación salarial por cuantil de ingreso
En este último apartado se muestran los resultados de la descomposición de brecha salarial por cuantil, incluyendo la inversa del ratio de Mills como una aproximación a la solución para el problema de sesgo de selección de Heckman (1977).
Como se muestra en la Gráfica 7a, la diferencia salarial se observa principalmente en los extremos, es decir, aproximadamente en 10% más pobre y en 15% más rico de la población de Chile. Para los valores intermedios la brecha salarial disminuye y se hace muy cercana a cero. Finalmente, la discriminación (diferencia asociada con coeficientes) también se da sobre todo en los extremos (en las proporciones 5% de la población más pobre y 5% más rica), y en tramos más intermedios esta discriminación es prácticamente cero.

Fuente: elaboración propia con base en datos de la Casen.
Gráfica 7 Descomposición por decil de ingreso según modelo deMelly (2006)
Por otro lado, en la Gráfica 7b se puede observar que han habido grandes cambios entre 1990 y 2017, principalmente en la mitad con menores ingresos. En dicha mitad se presenta en 1990 una discriminación menor que en los años posteriores; en el año 2000 ésta se eleva para casi la totalidad de este tramo, y en 2009 vuelve a disminuir. Por último, en 2017 la discriminación fue mayor en el extremo más pobre de la población, pero luego volvió a reducirse, en comparación con los otros años, para valores intermedios.
En cambio, en la mitad de mayores ingresos la discriminación es bastante similar en 1990, 2000 y 2009, mientras que en 2017 fue menor que en los años anteriores en los cuantiles intermedios, pero más alta en los extremos. En todos los casos ésta se concentra principalmente en la décima parte de la población con mayores ingresos.
V. Discusión y conclusiones
Existe un amplio debate en la literatura acerca de si la desigualdad salarial entre hombres y mujeres alimenta o perjudica el crecimiento económico y el desarrollo de los países (Kabeer y Natali, 2013). Este trabajo, con base en datos de la Casen de Chile para el periodo 1990-2017, analiza y desglosa la brecha salarial entre hombres y mujeres con el fin de estudiar, cuantificar y ver la evolución en el tiempo de la discriminación salarial por género en Chile.
La primera observación importante es que la brecha en la participación laboral ha ido disminuyendo en las últimas décadas, cuando llegaba a 150.8% en 1990 y en 2017 llegó a 55.7%; se redujo en 63.1% en este lapso de 27 años. Por otro lado, para todo el periodo se ha observado una brecha salarial en favor del hombre, aunque bastante inestable: entre 6 y 16%. Finalmente, quizás el resultado más importante de esta sección es que la brecha en años de educación es muy distinta cuando comparamos a las personas con empleo y a las desempleadas. Se observa para todo el periodo que los hombres con empleo tienen menos años de educación que las mujeres en la misma situación (entre 10 y 20% en todo el periodo), mientras que los hombres sin empleo tienen más años de educación que las mujeres en esta condición, aunque este valor se ha ido reduciendo en el tiempo. Esto quiere decir que, además de la discriminación salarial que estudia este trabajo, existe otro tipo de discriminación más silenciosa. Este simple resultado nos indica que las mujeres deben tener más años de educación para obtener un empleo con menor salario que un hombre, lo cual refleja que la discriminación hacia las mujeres también está presente en el acceso al empleo, lo cual, entre otros temas, provoca la discriminación en los salarios.
En esta investigación se han usado cuatro metodologías distintas para analizar y descomponer la brecha salarial en Chile; todas indican que el componente asociado con productividad (sus características) está en favor de la mujer y ayuda a disminuir la brecha salarial entre 10 y 20 puntos porcentuales -10.5% en 2017 con el modelo de Oaxaca y Ransom (1994)-, aunque ha ido disminuyendo lentamente desde 1990. Esto quiere decir que, si comparamos a una mujer con un hombre con las mismas características, igualmente calificados, la mujer recibirá un sueldo 10.1% menor al del hombre en promedio.
Por otro lado, la discriminación salarial llega a 17.1% en 2017, cuando se puede nuevamente descomponer entre el favoritismo hacia los hombres (6.6%) y la discriminación pura hacia las mujeres (10.5%) mediante el modelo de Oaxaca y Ransom (1994).
Sin embargo, estas clásicas ecuaciones de salarios presentan un sesgo de selección, ya que, por la naturaleza del tema, solamente podemos incluir personas que se encuentran trabajando y tienen un salario, es decir, no observamos a los desempleados. Es por esto que se debe corregir la estimación mediante la metodología de Heckman (1977).
Se corrobora además la importancia de corregir por sesgo de selección, ya que las estimaciones son muy sensibles a dicha corrección. Cuando realizamos esto, nos damos cuenta de que la estimación anterior subestima la discriminación salarial. Donde antes se calculaba que la discriminación salarial llegaba a 17.1%, una nueva estimación con corrección por sesgo de selección muestra que ésta ha estado entre 50 y 80% de 1990 a 2017, cuando lo más preocupante es que iba disminuyendo desde 1990 hasta 2003 (82.3% en 1990 y 52.6% en 2013), pero se ha estancado en estos niveles (49.7% en 2017). Finalmente, se descompone la discriminación salarial y se muestra que 4.5% está asociado con el favoritismo y 45.2%, con la discriminación pura en 2017. Estos resultados nos muestran que la magnitud de la discriminación salarial está fuertemente subestimada cuando no se corrige por sesgo de selección.
Desde una perspectiva histórica, evaluamos cómo ha evolucionado la discriminación salarial en Chile. Nos centramos en el modelo de Oaxaca y Ransom (1994) con corrección por sesgo de selección, y así se muestra que la discriminación laboral en el periodo de 1990 a 2003 disminuyó significativamente, pero luego esta disminución se frenó, y se mantuvieron valores constantes hasta la fecha de la última encuesta, 2017. Ésta es una conclusión preocupante, ya que se muestra que, en temas de discriminación salarial, Chile casi no ha mejorado en los últimos 15 años, cuando en la última década del siglo pasado sí había una mejoría.
Finalmente, aunque de manera más superficial, este documento muestra que casi toda la brecha salarial se encuentra en los extremos más pobres y más ricos cuando separamos por cuantiles de ingreso. Además, este trabajo estudia la descomposición en salarios, pero por variable, en la que se muestra que la mayor parte de la discriminación salarial ocurre en la experiencia laboral; asimismo, se observa que los años de educación ayudan a disminuir la discriminación salarial. Esto ocurre debido a que las mujeres con empleo tienen más años de educación que los hombres con empleo, es decir, les cuesta más tiempo de estudios obtener un trabajo peor pagado.











 nueva página del texto (beta)
nueva página del texto (beta)


