Introducción

La “nueva interpretación” (NI) de la teoría marxista del valor, planteada en la década de los ochenta (^{Duménil, 1980}; ^{Foley, 1982}), ha inaugurado una nueva era para la investigación empírica con base en el concepto de “expresión monetaria del tiempo de trabajo” (MELT, por sus siglas en inglés), definido como el cociente entre el valor agregado monetario total y el tiempo de trabajo total de los trabajadores productivos. La esencia de la NI radica en su capacidad para obtener magnitudes de valor a partir de datos sobre precios observables, a lo cual se le conoce como la “transformación inversa”, pues su dirección es contraria al procedimiento de Marx para transformar valores en precios. Al principio la NI se concentraba en la relación entre los agregados macroeconómicos, como el valor monetario total agregado y el tiempo de trabajo total de toda la economía. Recientemente, sin embargo, comenzó a aplicarse el método NI a nivel de industria (^{Rieu, 2008}; ^{Duménil, Foley y Lévy, 2009}), lo que dejó claro que la operacionalización de la NI a tal nivel requiere una tasa de plusvalía nivelada (^{Rieu, 2009}). ^{Foley (2016} y ²⁰¹⁸⁾ y ^{Cogliano (2021)} hicieron el intento de legitimar este supuesto mediante un comportamiento equilibrado del salario y el esfuerzo laboral de los trabajadores. En la misma línea ^{Cogliano (2018)} realizó un estudio empírico de la economía estadunidense que mostró una divergencia entre la producción de plusvalía y su realización a nivel industrial.

Sin embargo, como muestra la siguiente cita, los análisis de Foley-Cogliano se construyen sobre el supuesto de que los trabajadores “sienten” el grado aproximado de explotación o, dicho de otro modo: “el trabajador sí tiene acceso a su propia experiencia subjetiva” (^{Foley, 2016: 381}). “A pesar de que es imposible medir el esfuerzo laboral de manera ‘objetiva’, los trabajadores sí saben cuánto esfuerzo laboral se requiere en varios empleos y ‘votan con sus pies’ para equilibrar la relación entre el esfuerzo laboral total y los salarios monetarios” (^{Foley, 2018: 565}).

No obstante, aunque este supuesto es plausible, sólo proporciona “una referencia abstracta” (^{Foley, 2016: 382}). Nunca puede garantizarse que la economía real se encuentra en el estado de equilibrio de largo plazo, donde la tasa de plusvalía es igual en todas las industrias.

El propósito de este artículo es proponer una forma alternativa de estimar la tasa de plusvalía a nivel de industria sin asumir la igualación de dicha tasa. Mediante el método de la transformación inversa basado en la NI se demostrará que la tasa de plusvalía a nivel de industria puede estimarse a partir de los datos sobre la participación de los ingresos del trabajo en el ingreso total a ese mismo nivel. Este método proporciona una alternativa al método de Foley-Cogliano que, sin embargo, comparte el espíritu de la NI.

El resto del documento se encuentra organizado de la siguiente manera: en la sección I se presenta de forma breve la transformación inversa de la NI; en la sección II se formaliza la metodología, y en la sección III se muestran las estimaciones de las relaciones marxistas de valor en el nivel de la industria mediante datos de Corea del Sur. Finalmente, en la sección IV se discuten las conclusiones del estudio.

I. La metodología de la transformación inversa: la nueva interpretación

Respecto de la estimación empírica de indicadores marxistas, la contribución más importante de la NI radica en que es capaz de partir directamente de los datos de precios observables. Aquí el concepto de MELT es una variable central que se define como el cociente entre el valor agregado total y el tiempo de trabajo total. Uno de los aspectos que distinguen a la NI es que el valor de la fuerza de trabajo no se reduce al valor de los bienes de salario como en la literatura convencional, sino que se define como la tasa salarial dividida entre la MELT.

Al hacer la distinción entre trabajo productivo e improductivo de manera explícita, como en este artículo, sería más preciso considerar la MELT como “la expresión monetaria del tiempo de trabajo productivo” (^{Foley, 2016: 379-380}).¹ Además, el valor de la fuerza de trabajo se obtendría como la tasa salarial del trabajo productivo dividida entre la MELT.

A fin de expresarlo formalmente, los términos L_P y L_U denotan el tiempo total de trabajo de los trabajadores productivos y el de los improductivos, respectivamente. Mientras que w_P y w_U representan la tasa salarial de los trabajadores productivos y la de los improductivos, respectivamente. De tal modo que W_P = w_PL_P y W_U = w_UL_U corresponden a la masa salarial total de los trabajadores productivos y la de los trabajadores improductivos, en ese orden. VA es el valor agregado total.

Ahora bien, mediante la definición MELT = VA/L_P , el valor de la fuerza de trabajo, denotado por ω, se obtiene como:

En la NI la tasa de explotación, equivalente a e, se expresa de la siguiente manera:

En la ecuación (2) se muestra que la tasa de plusvalía no es igual a la relación ganancia agregada-salario, porque la tasa salarial de los trabajadores improductivos no se cuenta en el denominador.

Una discrepancia similar a la que existe entre la tasa de plusvalía y la relación ganancia agregada-salario se identifica en la correspondencia entre el valor de la fuerza de trabajo y la participación del trabajo en el ingreso. En la NI, cuando no se hace la distinción entre trabajo productivo e improductivo, el valor de la fuerza de trabajo es igual a la participación del trabajo en el ingreso; cuando existe la distinción, los dos ya no son iguales entre sí. Para ver esto denotemos la participación del trabajo en el ingreso mediante LS; así, de acuerdo con su definición, se tiene:

Al comparar las expresiones (1) y (3) se reinterpreta el valor de la fuerza de trabajo como sigue:

A partir de la ecuación (4) es fácil saber que el valor de la fuerza de trabajo siempre será menor que la participación de los trabajadores en el ingreso en la medida en que haya trabajadores improductivos, de modo que W_U /W_P ≠ 0. Esto se debe a que en la literatura de la teoría marxista del valor el salario del trabajo improductivo se considera una deducción de la plusvalía producida por el trabajo productivo. Si la participación de los trabajadores improductivos en la masa salarial total (W_U/W_P) aumenta, entonces la diferencia entre el valor de la fuerza de trabajo y la participación de los trabajadores en el ingreso (LS/ω), también lo hará.

Debido a que, con base en la ecuación (4), el valor de la fuerza de trabajo está correlacionado con la participación del trabajo en el ingreso, la tasa de plusvalía también puede reescribirse como correlacionada con la participación del trabajo en el ingreso:

Como se ha mostrado en lo expuesto hasta ahora, en esencia la NI tiene la intención de examinar la economía a nivel agregado, en concordancia con la postura de la NI de que la teoría del valor-trabajo es una teoría macro. El objetivo de este documento es aplicar el marco de la NI a nivel industrial. Por un lado, ^{Foley (2016} y ²⁰¹⁸⁾ y ^{Cogliano (2021)} adoptan el supuesto de una tasa de plusvalía uniforme como conclusión lógica del método de largo plazo de Marx. Por otro lado, aquí se propone un supuesto alternativo, que arroja tasas de plusvalía diferentes entre las industrias.

Este enfoque se basa en la metodología de la transformación inversa.

II. La metodología de la transformación inversa: nivel de industria

La MELT de la i-ésima industria, denotada como MELT_i , se define de la siguiente manera:

Donde VA_i y L_i representan el valor monetario agregado y el tiempo total de trabajo de la i-ésima industria, respectivamente.²

Con base en la distinción de ^{Rieu (2008)} entre la “expresión de valor del tiempo de trabajo” (VELT) y la “expresión monetaria del valor” (MEV),³ el valor de una unidad de fuerza de trabajo y el de la tasa de plusvalía de la i-ésima industria son:

Mientras que la ecuación (7) es una aplicación simple de la NI a nivel industrial, la (8) requiere una explicación más detallada. Como una hora de trabajo en el i-ésimo sector produce horas de valor VELT_i , la plusvalía en el i-ésimo sector es igual a VELT_i menos el valor de una unidad de fuerza de trabajo. Es decir, la tasa de plusvalía es una función tanto de VELT_i como de ω_i .

El supuesto de Foley-Cogliano de la tasa nivelada de plusvalía implica, para cualquier i,j tal que i ≠ j, que:

La expresión (9) implica que la capacidad de creación de valor del trabajo individual es proporcional a su salario. Por lo tanto, la información sobre la expresión de valor del tiempo de trabajo de cada industria (VELT_i) es necesaria para realizar la transformación inversa de precios y datos tecnológicos en valores. Este punto ya se ha señalado anteriormente:

Una de las principales contribuciones de la NI es que conecta directamente valor y precio. Como la tasa de explotación para la economía total (e) es igual a la relación ganancia-salario agregados (π) en la NI, el supuesto de una tasa de explotación nivelada permite recuperar los valores de las mercancías individuales a partir de datos observables sobre precios de mercado (p), tasas de ganancia sectoriales (R) y tecnología (a).

[...] En un caso general, sin embargo, debemos volver a (3) [ecuación de valor a través de la transformación inversa de Rieu y Park] con n ecuaciones y 2n incógnitas [...] La cual estará indeterminada a menos que uno explique el mecanismo para determinar la expresión de valor del tiempo de trabajo a nivel sectorial [^{Rieu, 2009: 569-570}; cursivas añadidas].

Se puede interpretar que el método de Foley-Cogliano responde al punto anterior al introducir la condición de tasa de plusvalía nivelada, lo que implica que la tasa de salario relativo es igual a la expresión del valor relativo del tiempo de trabajo (^{Rieu, 2008: 570}).⁴ Esta solución es incompleta, porque no hay garantía de que una economía real se encuentre en la posición de equilibrio a largo plazo.

El supuesto alternativo aquí propuesto son las VELT_i ecualizadas. Desde esta propuesta, VELT_i puede normalizarse a la unidad, en cuyo caso la ecuación (8) se convierte en:

Con ello, la tasa de plusvalía ya no tiene que igualarse entre las industrias. La ecuación (10) parece ser una aplicación simple de la NI, y en este sentido la condición de una VELT nivelada es restrictiva. Sin embargo, desde este supuesto es posible estimar las tasas sectoriales de plusvalía, debido a las participaciones laborales sectoriales en el ingreso. En un principio, la ecuación (10) distorsiona sistemáticamente la (8). Si la mano de obra en el i-ésimo sector es mano de obra calificada superior al promedio, la ecuación (10) subestima la tasa de plusvalía del sector. A fin de pasar de la tasa de plusvalía a su equivalente en precio, es necesario conocer la VELT_i . Sin embargo, en la transformación inversa de la participación del trabajo sectorial en la tasa de plusvalía sectorial, podemos obtener las estimaciones mediante la ecuación (10). Sin duda este cálculo es una primera aproximación, porque no se refleja el efecto de VELT_i diferenciales. No obstante, podemos obtener una estimación creíble sobre la tendencia de las tasas sectoriales de plusvalía en la medida en que puede suponerse que la expresión del valor relativo del tiempo de trabajo es estable durante un cierto periodo.

En la siguiente sección aplicamos la transformación inversa con el fin de estimar las tasas sectoriales de plusvalía en la economía de Corea del Sur. No obstante, antes de hacerlo, hay un aspecto de la economía de este país que requiere especial consideración para propósitos de una estimación precisa: su proporción de trabajadores por cuenta propia es tan grande que cualquier estimación que no la tenga en cuenta de manera explícita estará probablemente sesgada.⁵ Debido a que el trabajo por cuenta propia tiene un carácter mixto de empleador y empleado, es común en la literatura considerar que los ingresos de los trabajadores por cuenta propia tienen un carácter mixto de salario y ganancia, a lo que suele llamarse ingreso mixto. Por ello, al utilizar directamente la ecuación (10) para estimar e_i mediante el uso de datos sobre remuneraciones al trabajo para w_i, no se logra una medida precisa del salario en tal industria, pues se ignora la parte salarial del ingreso mixto de la persona que trabaja por cuenta propia.

Con el fin de solventar este problema, se propone usar una forma indirecta al recurrir a la participación del trabajo en el ingreso. La literatura sugiere varios métodos para medir esta última considerando de manera explícita el ingreso mixto. Por lo tanto, si la relación entre la tasa de plusvalía y la participación del trabajo en el ingreso a nivel agregado -demostrada en la ecuación (5) - puede aplicarse a nivel de industria, entonces es posible estimar las tasas sectoriales de plusvalía en el sentido de la ecuación (10), pero con base en la cuestión del ingreso mixto de manera explícita.

Se propone la transformación inversa con base en la participación del trabajo en el ingreso como se explica a continuación. En primer lugar, la participación del ingreso laboral de la i-ésima industria, denotada por LS_i, se calcula como:

Por otra parte, el valor equivalente de la participación del trabajo en el ingreso de la i-ésima industria (LS_i^VALUE) se define como:

Aquí V_i, S_i y e_i son el capital variable, la plusvalía y la tasa de plusvalía de la i-ésima industria, respectivamente.

Al combinar (10), (11) y (12) se obtiene:

Mediante (12) y (13) la tasa de plusvalía de la i-ésima industria se calcula como:

Dadas la MELT y las MELT_i, la tasa de plusvalía puede calcularse al transformar inversamente la participación del trabajo en el ingreso a nivel de la industria mediante la ecuación (14).

Por otro lado, la relación ganancia-salario de la i-ésima industria está denotada por e_i^PRICE, que es el precio equivalente de la tasa de plusvalía y se expresa como:

Las ecuaciones (14) y (15) demuestran que la relación entre la MELT y las MELT_i determina la relación entre la tasa de plusvalía y la relación ganancia-salario a nivel de industria. Si MELT > MELT_i, entonces e_i > e_i^PRICE . Ello implica que la explotación es más intensa que cuando se mide en términos de precios. También conlleva a que parte de la plusvalía producida en la i-ésima industria se transfiere a las otras industrias. Además, MELT > MELT_i sugiere que la plusvalía producida en las otras industrias se transfiere a la i-ésima industria.

A partir de la ecuación (9) puede saberse que la nivelación de la tasa salarial más el supuesto aquí sugerido resulta en una tasa nivelada de plusvalía, es decir, el supuesto de Foley-Cogliano. Esto no significa necesariamente que la alternativa propuesta sea más débil que el supuesto de Foley-Cogliano, pues este último permite VELT_i diferenciales sólo en la medida en que sean proporcionales a las diferencias salariales. Sin embargo, una diferencia fundamental es que la alternativa propuesta se centra en la transferencia del valor ya producido en cada sector, mientras que Foley-Cogliano supone desde el principio una tasa nivelada de plusvalía como resultado final. En pocas palabras, el proceso de determinación de la participación del trabajo en el ingreso a nivel de industria se compone de los siguientes dos procedimientos:

Por la condición de que VELT_i es proporcional a w_i, Foley-Cogliano supone que la expresión (1) determina la (2). Lo que es más, la tasa uniforme de plusvalía como resultado final de estas dos expresiones se presupone de facto desde el principio. Por el contrario, la metodología aquí propuesta trata de estimar la tasa de plusvalía sectorial al centrarse en la expresión (2), mientras que la (1) se establece como desconocida. Esto también se relaciona con la búsqueda del intercambio desigual entre sectores mediante la diferencia entre la MELT y las MELT_i.

Como ambos métodos no están libres de la crítica de ^{Rieu (2008} y ²⁰⁰⁹⁾ a la NI, no puede concluirse que uno de ellos sea mejor que el otro. Sin embargo, sin estimar directamente las VELT_i, es necesario elegir uno u otro. En particular, dado que una economía puede estar o no en la posición de equilibrio de largo plazo, parece necesario adoptar el supuesto que se propone en este trabajo.

III. El caso de Corea del Sur

A fin de verificar la metodología de transformación inversa presentada en la sección anterior, se aplica a las estadísticas de Corea del Sur para el periodo de 1995 a 2015. Mediante el método de ^{Jeon y Joo (2015})⁷ primero se estima la participación del trabajo en el ingreso (LS_i) de la ecuación (11) en las industrias productivas. Una vez obtenidas la MELT y las MELT_i, es posible calcular el valor equivalente de la participación del trabajo en el ingreso, LS_i^VALUE, y luego las tasas de plusvalía a nivel de industria.

Cuando se tiene en cuenta la distinción entre trabajo productivo e improductivo, como en este estudio, es más probable que improbable que MELT sea mayor que MELT_i para la mayoría de las industrias productivas, pues existe una transferencia de valor sistemática de éstas a las improductivas. En este sentido, examinar los niveles relativos y las tendencias generales de las MELT_i en comparación con la MELT para las industrias productivas es más importante que preguntarse si las MELT_i son mayores que la MELT o no. Se puede interpretar que un aumento (una disminución) en el cociente MELT_i / MELT implica que la posición de la i-ésima industria en la transferencia de valor entre industrias está mejorando (empeorando), y que la condición de acumulación para la i-ésima industria en términos de producción e intercambio se está fortaleciendo (debilitando). La Gráfica 1 ilustra la MELT_i de cada industria productiva en relación con la MELT.

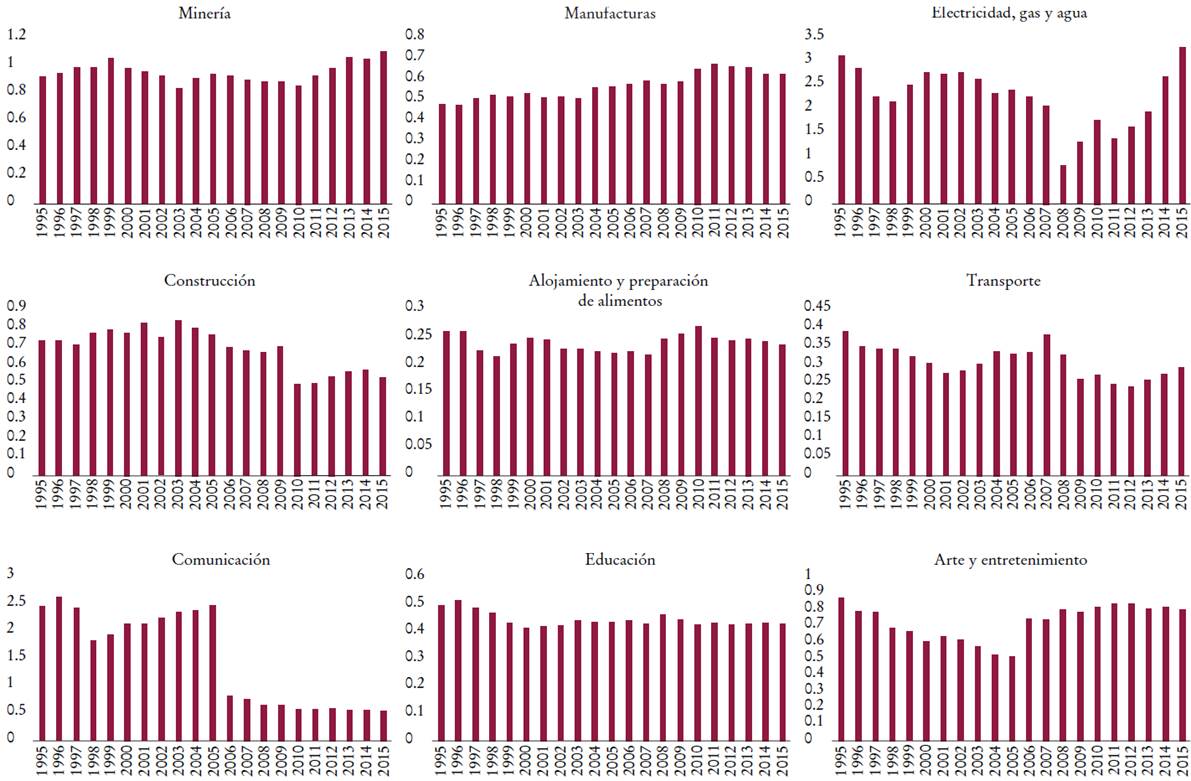
Fuente: elaboración propia.

Gráfica 1 La expresión monetaria del tiempo de trabajo en las industrias productivas 

El resultado empírico ilustrado en la Gráfica 1 confirma la predicción de que las MELT_i en las industrias productivas serían menores que la MELT. En la mayoría de los casos, MELT_i /MELT es menor que 1, con un par de excepciones que se analizarán a continuación. Las industrias productivas que se desempeñaron relativamente bien en términos de transferencia de valor fueron la industria manufacturera, la construcción y las artes, así como el entretenimiento, con coeficientes MELT_i /MELT de alrededor de 0.5 y más, mientras el alojamiento y la preparación de alimentos, la educación, y el transporte resultaron en coeficientes relativamente débiles, por debajo de 0.5. Según los datos originales, es en este último grupo de industrias donde se concentra la mayor parte de los trabajadores por cuenta propia. Por lo tanto, el débil desempeño de estas industrias en términos de transferencia de valor puede entenderse como un reflejo de la situación económica inferior de los trabajadores por cuenta propia respecto del resto de la economía de Corea del Sur.

Las excepciones a las industrias productivas que exhiben MELT_i menor que MELT, es decir, (MELT_i /MELT) < 1, son las industrias de minería; electricidad, gas y agua, y comunicación. Una posible explicación es que éstas se caracterizan por el monopolio natural, y están protegidas por una barrera de entrada a la competencia que nivelaría la tasa de ganancia. Si una determinada industria tiene un poder de mercado que le permite el control de precios, su MELT_i puede ser mayor que la MELT.

Con el fin de examinar con más detalle la tendencia relativa de MELT_i / MELT de cada industria a lo largo del tiempo, la Gráfica 2 reproduce el resultado de la Gráfica 1, con la diferencia de normalizar 1997 = 1.⁸ La observación más interesante en la Gráfica 1 es la industria manufacturera, que muestra una clara tendencia al alza desde la crisis de 1997-1998 y una clara tendencia a la baja desde 2011. En otras palabras, la industria manufacturera es la única que experimentó una mejora persistente en la condición de acumulación durante el largo plazo que se extiende desde el comienzo del periodo de estudio y hasta alrededor de 2010. También es el único sector que ha experimentado un persistente deterioro de la condición de acumulación desde 2011 hasta años recientes.

Fuente: elaboración propia.

Gráfica 2 Relación de Okishio en industrias productivas (1997 = 1) 

Dada la información sobre MELT y MELT_i en las Gráficas 1 y 2 los principales resultados de estimación de las tasas sectoriales de plusvalía se reportan en las Gráficas 3 y 4. La Gráfica 3 presenta la tasa de plusvalía (e_i) y la relación ganancia-salario (e_i^PRICE) de cuatro industrias productivas seleccionadas: minería, manufactura, construcción y educación. La Gráfica 4 expone los mismos indicadores para la manufactura a dos dígitos de desagregación: productos químicos, productos eléctricos y electrónicos, productos metálicos y equipos de transporte. Siendo que la diferencia entre dos cocientes está impulsada por MELT_i /MELT (véanse las ecuaciones [14] y [15]), también agregamos este último.

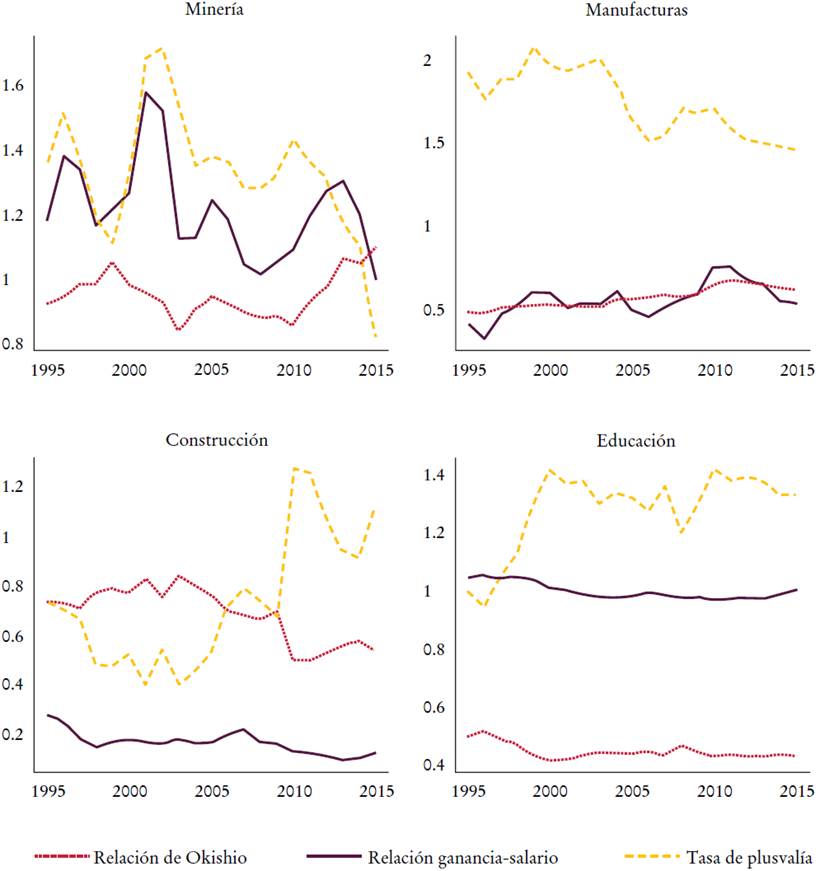
Fuente: elaboración propia.

Gráfica 3 La tasa de plusvalía y la relación ganancia-salario a nivel de industria 

Fuente: elaboración propia.

Gráfica 4 La tasa de plusvalía y la relación ganancia-salario de la manufactura a nivel de industria de dos dígitos 

El primer aspecto a resaltar es que, en la mayoría de los casos, la tasa de plusvalía es mayor que la relación precio-salario. Esto es lo que se esperaba de las ecuaciones (14) y (15) para industrias productivas que deben transferir valor a sectores improductivos, por lo que MELT_i es menor que MELT.

En segundo lugar, la tasa de plusvalía en la industria manufacturera fue excepcionalmente más alta que en las otras industrias reportadas en la Gráfica 3. Esto tiene que ver con el alto nivel de la relación ganancia-salario en esa industria.

En tercer lugar, obsérvese que la diferencia entre la tasa de explotación y la relación ganancia-salario en la manufactura se redujo constantemente hasta 2011, después de lo cual comenzó a crecer. Esta observación refleja directamente el desarrollo de la relación entre MELT_i y MELT de la manufactura que se discutió en relación con la Gráfica 2. De acuerdo con las ecuaciones (14) y (15), cuando el coeficiente aumenta (disminuye), la diferencia se reduce (crece).

El mismo método se aplica a la manufactura a nivel de industria de dos dígitos a fin de estimar la tasa de plusvalía y la relación ganancia-salario. Los resultados de las cuatro industrias manufactureras principales (petróleo, carbón y productos químicos; productos eléctricos y electrónicos; equipo de transporte, y metales) se ilustran en la Gráfica 4. La participación de estas cuatro principales industrias manufactureras en la producción total es de 83% en promedio anual. Se verifica que la tasa de plusvalía es consistentemente mayor que la relación precio-salario en estas cuatro industrias. Si bien es más o menos evidente que la brecha entre estos dos indicadores se redujo hasta 2011, es más fácil ver que dicha diferencia aumenta a partir de entonces. Esto sugiere que, al menos para estas cuatro industrias manufactureras, la disminución del cociente entre MELT_i y MELT -es decir, el debilitamiento de su posición en la relación de transferencia de valor- fue un factor importante de la dinámica de la tasa de plusvalía.

Estas observaciones pueden asociarse con que, durante aproximadamente una década después de la crisis de 1997-1998, las exportaciones manufactureras mantuvieron un aumento estable gracias a condiciones favorables en la economía global. Por ejemplo, la industria manufacturera registró una tasa de crecimiento de ventas de 10.38% durante este periodo de 10 años, que no obstante se redujo a -0.07% después de 2010 debido a la recesión mundial.⁹

La estructuración neoliberal desde la crisis económica asiática de 19971998 ha hecho que las fuerzas de la globalización tengan mayor influencia sobre la economía de Corea del Sur. La transferencia de valor de las industrias productivas hacia las improductivas aumentó constantemente después de la crisis de 1997 a 1998 y hasta mediados de la década del 2000.¹⁰ No obstante, la explotación en industrias improductivas se intensificó de manera notable al mismo tiempo, en particular inmediatamente después de la crisis de 1997 a 1998. La combinación de estas dos tendencias opuestas de acumulación de capital puede explicar que las condiciones para la acumulación de capital no se vieran tan socavadas en Corea del Sur durante 1995-2015, a pesar de que las actividades improductivas se expandieron de manera constante.

La industria manufacturera mantuvo consistentemente un nivel alto de la tasa de explotación durante la mayor parte del periodo, pero experimentó una tendencia decreciente alrededor de mediados de la década del 2000. Su MELT estuvo en constante aumento hasta 2011, después de lo cual comenzó a caer. Más importante aún: la manufactura fue la única industria productiva que experimentó una caída en la transferencia de valor a otras industrias hasta alrededor de 2010; después, nuevamente, fue la única industria productiva donde aumentó la transferencia de valor. Se puede concluir que la condición para la acumulación de capital en la industria manufacturera mejoró constantemente desde la crisis de 1997-1998, pero comenzó a deteriorarse después de 2011. Los factores asociados con la globalización, como el traslado de fábricas al exterior, podrían haber sido cruciales para mejorar las condiciones para la acumulación de capital en la industria manufacturera, lo cual se logró a pesar del constante aumento de los sectores improductivos. Sin embargo, parece que las condiciones para un crecimiento impulsado por las exportaciones comenzaron a colapsar desde 2010, y a partir de entonces, la economía de Corea del Sur entró en una coyuntura que requiere un cambio de régimen hacia un crecimiento impulsado por la demanda interna.

IV. Conclusiones

Con base en la nueva interpretación de la teoría marxista del valor, este artículo contribuyó con el método de transformación inversa para estimar la tasa de plusvalía a nivel de industria. Una de las novedades de este estudio es considerar explícitamente las tasas desiguales de plusvalía entre industrias. Sin el supuesto de una tasa nivelada de plusvalía como posición a largo plazo, es posible estimar la dinámica de las divergencias entre industrias productivas e improductivas. Como verificación empírica de la metodología, se examinó también la economía de Corea del Sur desde la perspectiva de la teoría marxista del valor. A fin de comprender las condiciones cambiantes de la acumulación de capital, el estudio se centró en el análisis de clase y la transferencia de valor intersectorial mediante la estimación de tasas de explotación sectoriales junto con las expresiones monetarias del tiempo de trabajo (MELT) sectoriales. El análisis teórico del valor proporciona una base para comprender el desarrollo desigual de la acumulación capitalista desde una perspectiva general.