Introduction
Until recently, Mexican authorities believed they have won the battle against inflation, which could distort both the decision making of economic agents and the performance of economic activities. Before 1973, the annual inflation rate was under five percent and a er July of that year the rate was more than ten percent. During the 1980s and most of the 1990s, the inflation rate skyrocketed; for instance, in 1987 it was nearly 160 percent. This macroeconomic variable was controlled in April 2000 when it began to decrease slowly to around 4.5 percent. No matter what the efforts of the monetary authorities were, in 2017 the inflation rate went up to more than six percent. Currently, Mexico's inflation climbed to 6.08 percent year-on-year in April 2021 due to the economic problems created by the Covid-19 pandemic since 2020.
One of inflation’s main problems is that it adds uncertainty to decisions taken by agents. Investment planning is more difficult because entrepreneurs do not know future sales of goods and services. As for banking intermediaries, issuing loans is much more complicated, given that the higher the inflation rate, the higher the implicit risk associated with firms’ loan applications. Therefore, the fall in credit will cause negative effects on productive activities and long-run economic growth, as predicted by practice and theory of finance and growth.
The theoretical relationship between bank credit and its long-term effects on growth has been studied extensively. The theory of finance and growth argues that operations of financial intermediaries influence positively on the level and rate of long-run output (Juhro et al., 2020; He et al., 2019). Levine (1997) argues that a financial system carries out five basic functions that reduce or eliminate information and transaction costs: a) it facilitates the trading, hedging, diversifying, and pooling of risk; b) it allocates resources; c) it monitors managers and exert corporate control; d) it mobilizes savings; e) and it facilitates the commercialization of goods and services. When intermediaries perform these functions efficiently, economic growth is improved through two channels. The first channel is capital accumulation. For instance, if intermediaries mobilize savings and allocate them to the best investment projects with the highest returns, then capital accumulation is positively linked to an increase in real output. On the other hand, the second channel is technological innovation. By supporting outstanding projects, better technologies could be adopted or created which at the same time reinforces productivity and real output growth.
Various models have connected inflation with bank credit and, in a broader sense, with financial development. Moore (1986) builds a Harrod-Domar-type model to show that inflation reduces financial deepening, the volume of real credit, and financing for capital formation. Boyd et al. (1996) construct a model to explain why inflation reduces rates of returns in financial markets and increases information asymmetries, while inflicting a fall in investment that is important for capital accumulation. Azariadis and Smith (1996) include information asymmetries to a monetary growth model to predict that under low inflation the monetary rate of growth enhances long-term economic growth. Other studies from Huybens and Smith (1998, 1999) share the idea that high-inflation economies do not reach steady output growth and have inefficient financial markets due to the association between inflation and nominal interest rates (see also Bittencourt, 2011).
There is abundant literature exploring the nexus between inflation and macroeconomic variables. There are models gauging the impact of inflation on gross domestic product (GDP) (Dinh, 2020; Kuzheliev et al., 2020; Goudy and Reddy, 2020; Uddin, 2021; Rivera et al., 2020; Alb and Durguti, 2019; Karki et al., 2020; Adaramola and Dada, 2018; Aydin, 2017), exchange rates (Ha et al., 2020; Khan et al., 2019; Ohemeng et al., 2021; Lahiri, 2019; Bacilar et al., 2019), monetary aggregates (Doan Van, 2020; Hossain, 2019; Dua and Goel, 2021; Al-Mutari et al., 2020; Evans, 2019; Abango et al., 2019), fiscal policy variables (Asandului et al., 2021; Bordo and Levy, 2021; Fasanya et al., 2021; Ologbenla, 2019), stock market (Jelilov et al., 2020; Singh and Padmakumari, 2020; Okorie et al., 2021), among others.
On the other hand, many models have been used to analyze the interaction between inflation and bank credit, or in a broader sense financial development. The models include cross-country regressions (one and two-stage least squares, OLS), generalized method of moments (GMM, threshold OLS, etc.), times series (autoregressive vectors, VAR), Granger causality tests, vector error correction models (VECM) with weak exogeneity and principal components, autoregressive distributed lag model (ARDL, etc.), and panel models (generalized least squares, fixed and random effects, GMM, instrumental variables, VAR, VECM, semiparametric models, among others). Ikpesu (2021) studies a sample of sub-Saharan African countries during the 2000-2016 using a panel vector error correction model. The author’s results show that there is bi-directional causality between inflation and bank credit. Several studies have coincided on the following findings (Tinoco-Zermeño et al., 2014). Baum et al. (2009, 2006) and de Gregorio and Sturzenegger (1994) demonstrate that inflation and its volatility distort credit allocation and quality if intermediaries are unable to distinguish between good and bad borrowers. Boyd et al. (2001), Rousseau and Wachtel (2002), Rousseau and Yilmazkuday (2009), Bittencourt (2011) and Huang et al. (2010) show the negative association between inflation, bank credit to private sector, bank assets, and even liquid liabilities.
More recent studies such as Khan (2016) and Almaki and Batayneh (2015) also attest to the existence of an inverse relationship between inflation and bank credit. The first author finds out that 1% increase in inflation reduces credit by 0.16% in Pakistan; and the other authors obtained an inflation coefficient of -2.65 for Arabia Saudita. Katusiime (2018) investigates the link between credit to the private sector and inflation volatility. A salient finding is that inflation has a significant effect on private sector growth along with other determinants such as nominal exchange rate and lagged credit. Tinoco et al. (2018) examine data of inflation and credit of 84 countries over the 1980-2010 period with quantile panel regressions. In general, they concluded that the relationship between the two variables is nonlinear, statistically significant for underdeveloped countries and insignificant for developed countries. Additional relevant studies include Acharya et al. (2020), Galati et al. (2021), Lorente (2019), Corhay and Tong (2021), Ndou and Gumata (2017), and Sargolzaei and Bahrololoum (2019).
Another group investigates the effects of inflation on economic growth through the channel of financial development. Bandura (2020) analyzes 23 Sub-Saharan African countries with panel data from 1982 to 2016 and a non-dynamic threshold approach. The empirical results show that financial development enhances economic growth if inflation rates stay below 31%. In a similar vein, Mahawiya et al. (2020) underline price stability as a primary objective of monetary policy because an inflation rate higher than 17.9% in the Economic Community of West African States and higher than 14.5% in the Southern Africa Development Community hinders financial development. Bist (2018) assesses how financial development influences economic growth, and the price level is included as an explanatory variable. Private credit and the consumer price index are significant, although results are mixed. In 9 out of 16 countries, the effect of private credit on growth was positive and significant, whereas the price index was positive and significant in 13 countries, and negative in only one country. Ehigiamusoe et al. (2021b) employ the dynamic panel system generalized method of moments and the dynamic common correlated effects (CCE) in a panel of 125 countries to understand how inflation relates to financial development through GDP. According to the authors, inflation negatively regulates the positive effect of GDP on financial indicators in middle-income countries (see also Ehigiamusoe et al., 2021a; Baoko et al., 2017; Wu, 2021; Kagochi, 2019; Ouyang and Rajan, 2019; Ouyan, 2020; Saidi, 2020).
The objective of this paper is to show that inflation is negatively related to bank loans by using disaggregated annual data of Mexican states for the period 2003-2015. The period of study corresponds to macroeconomic stability with low inflation rates. Other studies have examined the link between credit and inflation under macroeconomic stability; see, for instance, Ikpesu (2021), Loganathan et al. (2017), and Sanusi et al. (2017). Coincidently, the study covers two government administrations under the National Action Party (PAN, for its acronym in Spanish) and the Institutional Revolutionary Party (PRI, for its acronym in Spanish). However, our focus is to quantify the effects of inflation on bank credit only and not on evaluating how government policies were successful at keeping inflation rates under control. On the other hand, we chose the mentioned period because in 2017 Banco de México changed of methodology of bank credit by economic activity according to an Agreement of the Instituto Nacional de Geografía y Estadística (INEGI) published on July 10, 2009 (Banco de México, 2021) to use the North American Industry Classification System (NAICS). Therefore, extending our data to recent years would make it inconsistent for empirical purposes.
The hypothesis of an inverse relationship between loans and inflation is explored by loan types (total credit, consumption credit, and mortgage credit) and loans to economic sectors (primary, secondary, and tertiary): we could disaggregate the credit series by using the methodology proposed by Bittencourt (2011), Fischer (1993), and Besley and Burgess (2003). Preliminarily, with our empirical model, we would expect to compute small or null coefficients, thus invalidating our principal hypothesis. In comparison to other studies, we employ panel-data cointegration that possesses two advantages (Bittencourt, 2011). On the one hand, the proposed panels lack the usual criticism of cross-section analysis in the sense that high-inflation periods would compensate low-inflation periods; in our case, the chosen period is of macroeconomic stability. In addition, panel models help to avoid problems of stationarity, heterogeneity bias, regional dependence, and endogeneity.
With respect to the methodology, we use panel data of the 32 Mexican states. A er applying the Im, Pesaran and Shin (IPS) (2003) test of unit roots for panel data and identify the level of cointegration of the variables (I(0) and/or I(1)), several models will be used: pooled OLS, fixed effects, random effects, mean group, pooled mean group, and dynamic fixed effects. In general, we conclude that inflation exerts a negative effect on credit issued by banks in the long run. This result is confirmed by the dynamic fixed effects estimation for total credit, consumption, and the services sector. Nonetheless, it is important to clarify that our hypothesis is invalid for the primary sector (agriculture, livestock, forestry, and fishing) and the secondary sector (industry). Moreover, based on the dynamic panel analysis we detected a positive short-run relationship between price increases and bank loans.
The organization of the rest of the document is as follows: in section 2, we discuss the regional distribution of commercial bank credit in Mexico, including branches, savings and debit accounts, credit card accounts, and concentration of banking activities within the country; in section 3, we introduce the empirical strategy and the model to be estimated; in section 4, we discuss the results from the multiple estimations; finally, in section 6, we give the conclusions.
Regional distribution of commercial bank credit in México
A major weakness of the Mexican economy is the low access to banking services, which could be caused by moderate level of financial competition (Castellanos et al., 2016; Herman and Klemm, 2019). Few individuals and companies can borrow money from banks to finance consumption or investment projects. Information from the Global Findex Database of the World Bank indicates that 51% of people were granted loans, although only 10% used formal financial intermediaries (Herman and Klemm, 2019). With respect to companies and according to the Enterprise Surveys, in 2010 only 27% of small and medium-sized companies had access to bank financing. Many factors could be at the root of those low percentages, but concentration in the banking system may be playing a decisive role (Herman and Klemm, 2019).
Table 1 shows the number of branches, debit card accounts, and credit card accounts that are mostly concentrated in Ciudad de México, Estado de México, Jalisco, and Nuevo León. With respect to branches, in 2003, those states concentrated 42.4% of total branches. The participation decreased to 40.6% in 2015 and to 40% in 2020. One reason of the decline is that some states increased their participation like Puebla and Veracruz, from 3.2 to 3.8% and 4.6 to 5.3% between 2003 and 2020.[a] As for debit card accounts, Ciudad de México, Estado de México, Jalisco, and Veracruz had 47.6% of total accounts in 2003. The distribution changed in 2015 and 2020, a er the share of Ciudad de México, Estado de México, Jalisco, Nuevo León, Sinaloa, and Veracruz jumped to 51% and 62% of total debit accounts. Finally, the most remarkable changes are seen in credit card accounts. At the beginning of the period, Ciudad de México had 43.8% of total accounts, followed by Jalisco with 8% and Nuevo León with 6.2%. As time passed, contracts were more dispersed throughout the country. Twelve years later, Ciudad de México had 17.7% of contracts, Estado de México 13.6%, Jalisco 8.2%, Nuevo León 5.3%, and Veracruz 5.5%, while the rest of states had substantial increases. In 2020 credit card accounts were concentrated in Ciudad de México (19.2%), Jalisco (8.1%), Estado de México (12.1%), Nuevo León (5.8%), and Veracruz (5%). In sum, credit cards were the most dynamic instruments that the banking system offered to more Mexicans.
Table 1 National Distribution of Bank Branches and Accounts.
| Number of branches | Savigns accounts contracts | Credict card contracts | ||||||||||
| 2003 | % | 2015 | % | 2003a | % | 2015a | % | 2003a | % | 2015a | % | |
| Aguascalientes | 67 | 0.9 | 123 | 1.0 | 0.11 | 0.9 | 1.1 | 1.1 | 0.14 | 1.0 | 0.26 | 1.1 |
| Baja california Norte | 248 | 3.2 | 358 | 2.9 | 0.38 | 3.2 | 3.5 | 3.3 | 0.28 | 2.1 | 0.73 | 3.0 |
| Baja california Sur | 55 | 0.7 | 100 | 0.8 | 0.08 | 0.6 | 0.8 | 0.7 | 0.04 | 0.3 | 0.18 | 0.8 |
| Campeche | 51 | 0.7 | 95 | 0.8 | 0.09 | 0.8 | 0.7 | 0.7 | 0.05 | 0.3 | 0.15 | 0.6 |
| Coahuila | 231 | 3.0 | 317 | 2.6 | 0.27 | 2.3 | 2.9 | 2.7 | 0.30 | 2.2 | 0.54 | 2.2 |
| Colima | 56 | 0.7 | 94 | 0.8 | 0.07 | 0.6 | 0.9 | 0.9 | 0.05 | 0.4 | 0.18 | 0.07 |
| Chiapas | 150 | 1.9 | 250 | 2.0 | 0.20 | 1.7 | 2.4 | 2.2 | 0.10 | 1.0 | 0.39 | 1.6 |
| Chihuahua | 279 | 3.6 | 374 | 3.1 | 0.37 | 3.1 | 3.4 | 3.3 | 0.30 | 2.2 | 0.67 | 2.8 |
| Ciudad de México | 1485 | 19.2 | 1787 | 14.6 | 3.06 | 26.1 | 19.1 | 18.2 | 5.91 | 43.8 | 4.35 | 17.7 |
| Durango | 86 | 1.1 | 116 | 0.9 | 0.12 | 1.0 | 1.2 | 1.1 | 0.11 | 0.8 | 0.26 | 1.0 |
| Guanajuato | 343 | 4.4 | 560 | 4.6 | 0.45 | 3.8 | 4.0 | 3.8 | 0.41 | 3.0 | 1.02 | 4.2 |
| Guerrero | 150 | 1.9 | 235 | 1.9 | 0.25 | 2.2 | 1.9 | 1.9 | 0.12 | 0.9 | 0.41 | 1.7 |
| Hidalgo | 106 | 1.4 | 201 | 1.6 | 0.21 | 1.8 | 1.8 | 1.7 | 0.10 | 0.8 | 0.43 | 1.8 |
| Jalisco | 658 | 8.5 | 1026 | 8.4 | 0.81 | 6.9 | 6.7 | 6.4 | 1.08 | 8.0 | 2.01 | 8.2 |
| Estado de México | 598 | 7.7 | 1302 | 10.6 | 1.12 | 9.6 | 10.7 | 10.2 | 0.59 | 4.4 | 3.33 | 13.6 |
| Michoacán | 272 | 3.5 | 407 | 3.3 | 0.46 | 3.9 | 2.6 | 2.5 | 0.27 | 2.0 | 0.79 | 3.2 |
| Morelos | 120 | 1.6 | 223 | 1.8 | 0.20 | 1.7 | 1.5 | 1.4 | 0.14 | 1.0 | 0.40 | 1.6 |
| Nayarit | 56 | 0.7 | 110 | 0.9 | 0.08 | 0.7 | 1.1 | 1.0 | 0.05 | 0.4 | 0.21 | 0.9 |
| Nuevo León | 545 | 7.0 | 853 | 7.0 | 0.34 | 2.9 | 6.2 | 5.9 | 0.83 | 6.2 | 1.30 | 5.3 |
| Oaxaca | 131 | 1.7 | 273 | 2.2 | 0.26 | 2.2 | 1.9 | 1.9 | 0.09 | 0.6 | 0.35 | 1.4 |
| Puebla | 246 | 3.2 | 488 | 4.0 | 0.42 | 3.6 | 3.5 | 3.4 | 0.38 | 2.8 | 0.93 | 3.8 |
| Querétaro | 126 | 1.6 | 209 | 1.7 | 0.20 | 1.7 | 1.6 | 1.6 | 0.15 | 1.1 | 0.39 | 1.6 |
| Quintana Roo | 227 | 2.9 | 316 | 2.6 | 0.30 | 2.6 | 3.1 | 3.0 | 0.22 | 1.6 | 0.59 | 2.4 |
| San Luis potosí | 236 | 3.1 | 318 | 2.6 | 0.30 | 2.6 | 3.1 | 3.0 | 0.22 | 1.6 | 0.59 | 2.4 |
| Sinaloa | 116 | 1.5 | 207 | 1.7 | 0.18 | 1.5 | 1.8 | 1.7 | 0.14 | 1.1 | 0.37 | 1.5 |
| Sonora | 285 | 3.7 | 390 | 3.2 | 0.27 | 2.3 | 3.3 | 3.1 | 0.31 | 2.3 | 0.70 | 2.9 |
| Tabasco | 46 | 0.6 | 78 | 0.6 | 0.08 | 0.7 | 0.7 | 0.7 | 0.02 | 0.2 | 0.16 | 0.7 |
| Tamaulipas | 285 | 3.7 | 390 | 3.2 | 0.27 | 2.3 | 3.3 | 3.1 | 0.31 | 2.3 | 0.70 | 2.9 |
| Tlaxcala | 46 | 0.6 | 78 | 0.6 | 0.08 | 0.7 | 0.7 | 0.7 | 0.02 | 0.2 | 0.16 | 0.7 |
| Veracruz | 353 | 4.6 | 666 | 5.4 | 0.58 | 5.0 | 5.2 | 4.9 | 0.57 | 4.2 | 1.34 | 5.5 |
| Yucatán | 121 | 1.6 | 224 | 1.8 | 0.12 | 1.0 | 1.5 | 1.4 | 0.18 | 1.4 | 0.42 | 1.7 |
| Zacatecas | 84 | 1.1 | 116 | 0.9 | 0.12 | 1.0 | 0.9 | 0.9 | 0.05 | 0.3 | 0.17 | 0.7 |
| Total | 7732 | 100.0 | 12234 | 100.0 | 11.74 | 100.0 | 104.9 | 100.0 | 13.49 | 100.0 | 24.50 | 100.0 |
Source: Own calculation with data from Comisión Nacional Bancaria y de Valores.
Note: * Figures in millions.
Bank loans to the private sector are also concentrated. Map 1 shows the distribution of total bank loans (A), consumption loans (B) and mortgage loans (C) as a percentage of GDP. Based on the maps, we can infer two facts. There was marked increase in total credit from 33 to nearly 60% from 2003 to 2015, but only in Ciudad de México. The remaining states still have low levels of bank loans. On the other hand, there were not important changes in mortgage and consumption loans. On the contrary, some states had credit falls in 2015. In addition, the map displays information on loans for the three major economic sectors. Panel D contains data for the primary sector of agriculture, livestock, forestry, and fishing. In 2003, Sonora and Sinaloa received most of the financing, followed by other Northern states. But in 2015 Chihuahua, Durango, and Coahuila obtained more credit, as well as other states from Central Mexico including San Luis Potosí, Guanajuato, and Michoacán. Regarding the secondary sector (E), in 2003 Nuevo León and Ciudad de México concentrated most credit, followed by Jalisco, San Luis Potosí, Estado de México and Puebla. Lastly, in the case of the services sector (F) Nuevo León and Ciudad de México (and some Central and Northern states) dominated in 2003, but in 2015 the distribution favored Sinaloa and Quintana Roo.
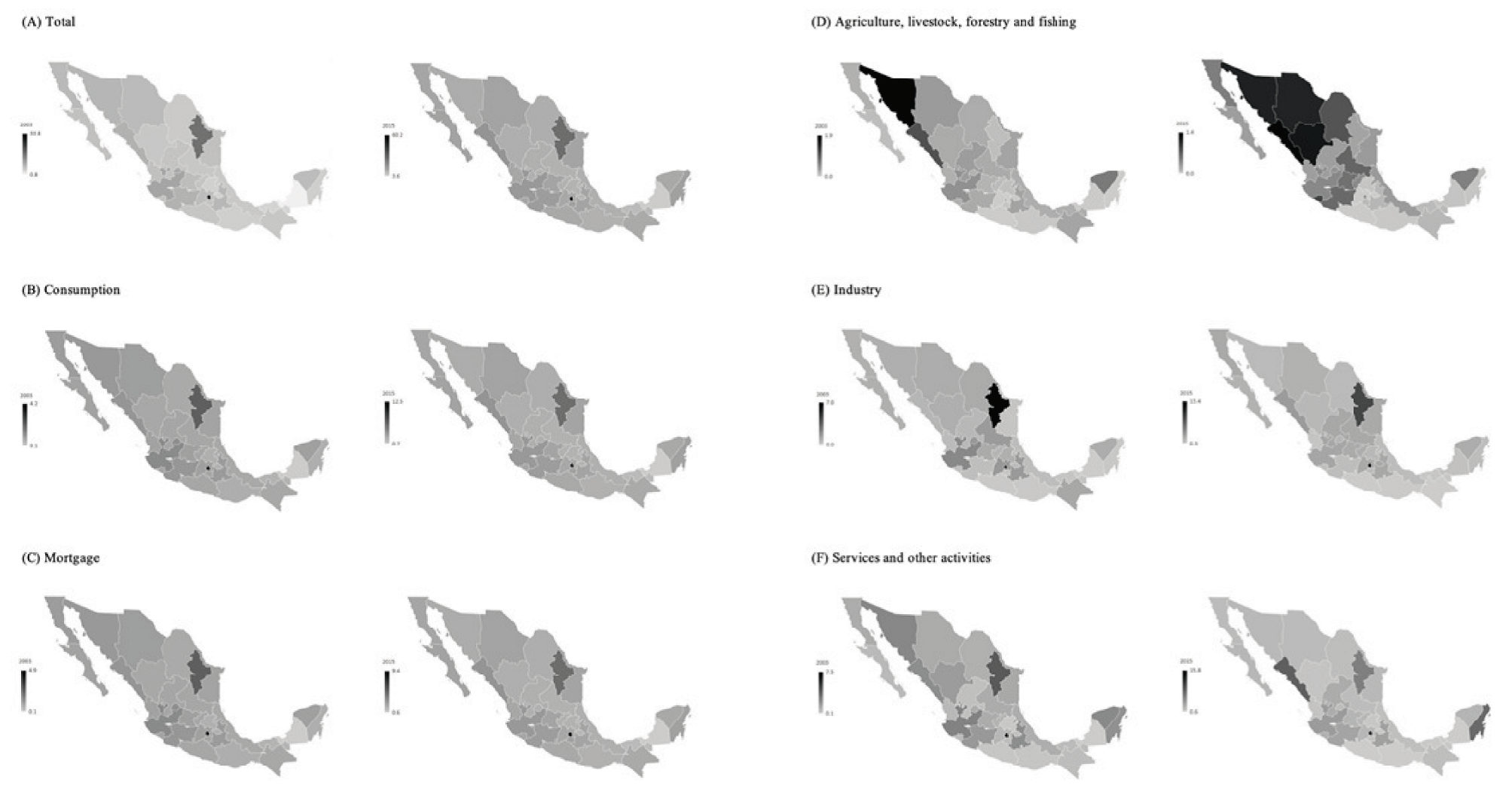
Source: Own elaboration with data from Banco de México.
Map 1 State Distribution of Bank Credit by Type (A-C) and Economic Sectors (D-F).
In fewer words, banking intermediation in Mexico is highly concentrated in some areas of the country. It is certainly correlated with population concentration and low financial competition. In terms of regional economics, the fact that only a handful of firms and individuals can obtain financing would limit positive diffusion effects of financing to neighboring states. This negative effect would be reinforced by an actual and expected higher inflation. In the forthcoming sections, we attempt to measure empirically the influence of inflation on bank credit.
Method
In this section, we briefly discuss the empirical methodology to estimate the effects of inflation on bank credit. First, we review the main characteristics of static and dynamic panel data estimators, including pooled OLS (POLS), fixed effects (FE), random effects (RE), mean group (MG), pooled mean group (PMG), and dynamic fixed effects (DFE). We then proceed to introduce the empirical model based on the Autoregressive Distributed Lag estimator (ARDL). Finally, we describe the data used in the estimations.
This paper proposes to study the link between inflation and bank loans with panel-data models. In contrast to simple OLS regressions, panel-data models could offer richer insights because they give regressions temporal and spatial features. Another reason is that they allow for the study of individual effects while at the same time compute consistent and unbiased coefficients (Castellacci, 2008). In our case, the data structure could potentially offer more information since it has been disaggregated by the 32 Mexican states.
In general, there are two types of panel-data models, namely static and dynamic. The static models are the pooled OLS, the fixed-effects model and the random-effects model. For the first model, intercepts and slopes are fixed and we would assume that there are no country/state nor temporal effects. The next model supposes that slopes are constant, but intercepts change according to the units, be it countries or states. The third model assumes that the unobserved individual heterogeneity is uncorrelated with the independent variables (Greene, 2012). However attractive those models could be, they have several shortcomings (Samargandi et al., 2015). Pooled OLS is very restrictive because it is based on a common intercept and slope coefficients for all cross-units. The limitation of the fixed effects model is that unit-specific intercepts vary, whereas in the random effects model time is unchanging. “In real life, this assumption is very o en invalid” (Samargandi et al., 2015, p. 70). Besides, static models do not consider the dynamic structure of the data which may be embedded. Also, these kind of estimators do not distinguish between short- and long-run relationships that are useful to scrutinize data over time (Loayza and Ranciere, 2006). Finally, the traditional random or fixed effect methods exclude cointegration issues that dynamic models usually consider, as we propose in this paper, to avoid the problem of endogeneity that may be present in variables. Even though the traditional estimators have these limitations, their estimation could be informative about the negative relationship between inflation and bank credit.
Following Loayza and Ranciere (2006) and Pesaran et al. (1999), we propose model of a dynamic heterogeneous panel and error correction based on the autoregressive distributed lag technique (p,q), where Importar p is the lag of the endogenous variable, and q is the lag of the exogenous variables:
where FIN is the proportion of bank loans to the private sector to GDP. Depending on the model at hand, FIN represents one of the six variables of interest, specifically total loans (CRE), consumption loans (CON), mortgage loans (MOR) or loans to the primary sector (SEC1), secondary sector (SEC2) or service sector (SEC3). x is a set of independent variables comprising the inflation rate (INF), general government spending as a proportion of GDP (GOV), and population. Additionally, γ and δ are the short-run coefficients of the lagged dependent and independent variables, respectively. The set of βs are the long-run coefficients, whereas the term Importar imagen corresponds to the coefficient of speed of adjustment to the long-run equilibrium. Letters i and t are state and time indexes, respectively. On the other hand, the equation in square brackets is the long-run equation that can be estimated with the following specification:
There are several advantages in applying the ARDL approach to cointegration. The first advantage is that cointegration can be tested when variables are I(0), I(1), or mutually cointegrated (Pesaran and Shin, 1996; Pesaran and Smith, 1998). This makes it attractive to put together growth and level variables in a model. In our case, it allows for the inclusion of inflation rate with the rest of level variables. Moreover, it renders unnecessary to test for unit roots, although we test for the presence of unit roots with the test developed by Im et al. (2003), as we will show below. Another advantage of the bounds testing approach is that cointegration is even possible when exogenous variables are endogenous, given that it calculates more precise long-run coefficients with valid t-values (Inder, 1993; Ang, 2008). Finally, with the method both the short- and long-run coefficients can be calculated concurrently while considering the time and cross-section dimensions of data.
Equation (2) can be estimated by using the MG model introduced from Pesaran and Smith (1995), the PMG model proposed by Pesaran et al. (1999), and the dynamic fixed effects (DFE) estimator. The first cointegration approach stipulates the estimation of individual regressions for each state (in our case) and then computes the parameters as unweighted means of the estimated coefficients. One key assumption of the approach to be valid is that N and T need to be sufficiently large. One of the differences of the PMG model in comparison to the MG model is that the former allows the short-run parameters being completely heterogeneous and the long-run coefficients are uniform across units. The reasoning for homogeneous long-run coefficients is that sometimes “budget or solvency constraints, arbitrage conditions, or common technologies are the same within a country” (Pesaran et al., 1999, p. 621). The dynamic fixed effects estimator is basically equal to the PMG estimator, although there is one important difference (Samargandi et al., 2015). For the long-run portion, the intercept and the error variance are equal in all states, as well as the error correction term and the short-run parameters.
Analysis
This research employs panel data that covers the 32 Mexican states from 2003 to 2015. The information was obtained from Banco de México, Instituto Nacional de Estadística y Geografía (INEGI), and Consejo Nacional de Población (CONAPO). From Banco de México we extracted series of bank loans for each Mexican state, which were then divided into total, consumption, mortgage, primary sector, secondary sector, and services sector. And from INEGI, we obtained annual state data for GDP, general government spending, and inflation. To linearize the series, we applied natural logs to all variables.
The data for bank loans required special treatment. On its website Banco de México warns that total bank loans include mortgage and consumption loans and other minor adjustments. However, consumption and mortgage loans are not disaggregated by federal entity. Given that our focus is to get a detailed understanding of the inflationary effects on bank loans, we decided to apply the method proposed by Bittencourt (2011), Honohan (2004), and da Silva (2002). The method proceeds as follows. Assuming that we have national data for total loans, consumption loans, and mortgage loans, we divided each series by each state’s GDP. Then, we multiplied the resulting figure by the corresponding percentage participation of each state in the national financial domestic product (FDP). The product is the value of the domestic product of financial institutions, as reported by INEGI within the domestic product of the services sector. Indeed, this weighting method of state data of bank loans capture more precisely the different levels of financial development (Bittencourt, 2011) within Mexico. For instance, a er weighting the variables we can see that in 2015 the value of total credit over GDP was 60% in the Ciudad de México and around 30% in Nuevo León. On the contrary, poorer states as Chiapas, Colima, and Oaxaca have low levels between 10 and 14%. The formula to calculate the state levels of bank credit is given by
where bank credit is one of the six national credit variables, GDP it is the state GDP, and FDP it and FDP t represent the national and state FDP, respectively.
Table 2 presents the descriptive statistics. Concerning bank credit, the highest mean is in total credit (11.42% of GDP), followed by consumption credit and mortgage loans. Disaggregating by sectors, the services sector has the highest mean with 2.1% of GDP. The average inflation rate was 4% during the whole period and government spending was on average 21.6% of GDP. Government spending and total credit have the highest standard deviations. The difference between minimum and maximum values reveals the economic and financial disparities among Mexican states. For example, the maximum value of 60.23% of GDP of bank credit belongs to Ciudad de México as well as government spending of 57.04% of GDP. However, in other less developed states the various types of bank credit do not reach 1% of GDP and government spending is low at 3.1% of GDP. Therefore, data from Table 2 coincide with the regional concentration of the banking indicators that we reviewed in the previous section. Moreover, we infer that the low levels of banking credit are detrimental to economic growth in Mexican states. According to the theory of finance and growth, unavailability of loans for investment and production purposes limit, for instance, the adoption of better technologies by firms to improve productivity. Given the minimum values of banking credit, it is evident that in some states firms have faced credit constraints and that medium and long-term growth has been compromised.
Table 2 Descriptive Statistics.
| Variable | Mean | St. dev. | Minimum | Maximum |
| CRE | 11.416 | 7.184 | 0.656 | 60.228 |
| CON | 2.483 | 1.629 | 0.096 | 12.516 |
| HOU | 1.860 | 1.185 | 0.149 | 9.436 |
| SEC1 | 0.318 | 0.346 | 0.005 | 2.203 |
| SEC2 | 1.763 | 2.010 | 0.022 | 13.367 |
| SEC3 | 2.133 | 2.293 | 0.101 | 15.803 |
| INF | 4.008 | 1.248 | 0.349 | 8.355 |
| GOV | 21.615 | 9.105 | 3.076 | 57.043 |
Source: Own elaboration.
On the other hand, in Figure 1 we depict the data of the inflation rate against the six credit variables. The negative relationship is more pronounced in total, consumption, and mortgage loans, and it is flatter in loans to the economic sectors. In sum, this preliminary evidence points out the presence of an inverse relationship between inflation and bank credit in Mexico
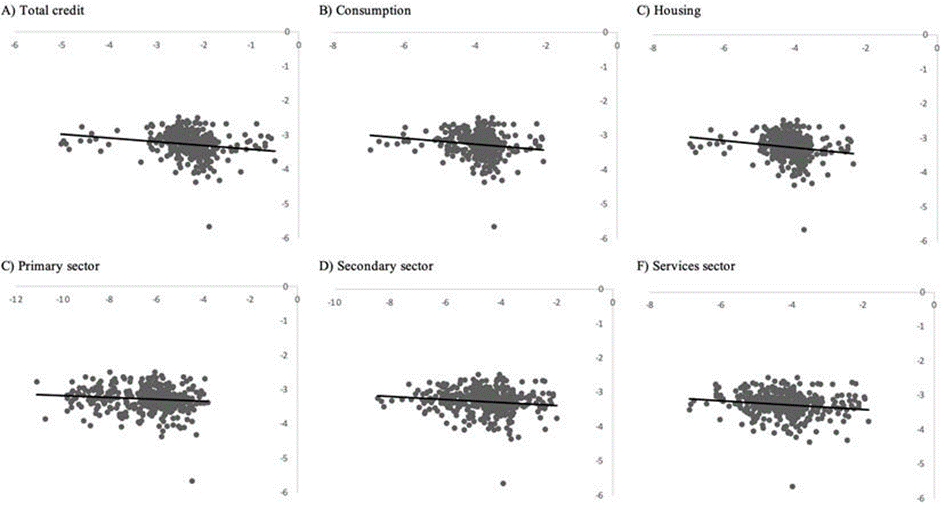
Source: Own calculation with data from Banco de México and INEGI.
Figure 1 Relationship between Inflation and Bank Credit, 2003-2015.
Before proceeding with the cointegration tests and to check for the validity of the ARDL bounds method, we use the Im et al. (2003) test for panel unit roots. We apply the test even if it is not necessary, as we said above, only to make sure that variables are I(0), I(1), or a combination of both. The IPS test specifies a separate Augmented Dickey Fuller regression for each cross section (states, in our case) of the panel data, and then the statistics are averaged. In comparison to other tests such as the one proposed by Levin et al. (2002), one of the advantages of the IPS test is that it is flexible with respect to the sample size and asymptotics (Bittencout, 2011). The state ADF equations of a variable Y and the IPS test, respectively, are as follows:
where αi is the heterogeneous constant term, δit represents the time trend, uit is the residuals, and N is the number of states in Mexico. The results of the IPS test are displayed in Table 3. We see that, in fact, all variables are either I(0) or I(1), and that none of them is integrated of higher order. Therefore, this allows us to apply the ARDL methodology to compute the short- and long-run coefficients.
Table 3 IPS Panel Unit Root Tests.
| Variables | Levels | First difference | Decision | ||
| Static | Sig. | Static | Sig. | ||
| CRE | -2.039 | ** | -3.623 | * | I(0) |
| CON | -11.951 | * | -8.075 | * | I(0) |
| HOU | -19.421 | * | -4.530 | * | I(0) |
| SEC1 | -1.459 | *** | -4.872 | * | I(I) |
| SEC2 | -3.634 | * | -6.188 | * | I(0) |
| SEC3 | -2.378 | * | -7.639 | * | I(0) |
| INF | -1.709 | ** | -8.706 | * | I(0) |
| GOV | 1.491 | -6.965 | * | I(I) | |
| POP | 2.016 | -2.312 | ** | I(I) | |
Source: Own calculations.
Note: *, ** and *** indicate significance at 1, 5 and 10%, respectively.
There are some strong assumptions concerning traditional estimators. For the pooled OLS estimation, inference needs to control for the possible correlation between the error correlation over time and correlation between units (Cameron and Trivedi, 2010). As for the fixed-effects panel regression, it is appropriate only if the slopes are homogeneous, which may not be the case for all Mexican states. If this assumption is not met in the presence of heterogeneous slopes, the estimator will be inconsistent, and the right-hand variables will be dependent on the lagged exogenous variable. On the other hand, the random-effects estimator considers heterogeneous intercepts and slopes to give more consistent and efficient estimators. In applied research, this estimator would be adequate when the units of analysis do not share the same level of economic development. In Mexico, heterogeneity arises when we look at the different regions. Northern and central states are more developed economically speaking than the rest of states (except for Jalisco). Such diversity would therefore validate the use of the random-effects method. Given these considerations and to choose the best static estimator, we use the F test and the Hausman test.
Table 4 exhibits the results of the traditional estimations. Panel I exhibits the pooled OLS estimation. In all regressions, the inflation variable has negative sign, indicating an inverse relationship between bank loans and the increase in prices. The calculated coefficients range from -0.042 for consumption loans to -0.192 for mortgage loans. In these regressions, although mostly statistically insignificant, government spending has negative coefficients. On the other hand, the population variable has positive parameters, implying a direct relationship between loans and the number of inhabitants. The high values of R2 suggest that the number of variables included in the regressions is sufficient to explain most of the variations of the dependent variable, e.g., bank credit.
Table 4 Panel Data Estimations of Inflation and Bank Credit for Mexican States.
| CRE | e.e | CON | e.e | HOU | e.e | SEC1 | e.e | SEC2 | e.e | SEC3 | e.e | |
| I. Pooled OLS (416 obs.) | ||||||||||||
| INT | -0.288 ** | 0.119 | -1.028 * | 0.220 | -0.528 * | 0.155 | -0.970 *** | 0.515 | -1.160 ** | 0.506 | -0.598 *** | 0.3241 |
| INF | -0.058 * | 0.013 | -0.042 **** | 0.024 | -0.070 * | 0.016 | -0.192 * | 0.064 | -0.085 | 0.056 | -0.085 ** | 0.036 |
| GOV | -0.003 | 0.010 | -0.016 | 0.018 | -0.003 | 0.012 | 0.051 | 0.048 | -0.105 ** | 0.042 | -0.029 | 0.027 |
| POP | 0.004 | 0.007 | 0.0288 ** | 0.012 | 0.008 | 0.008 | 0.003 | 0.029 | 0.023 | 0.027 | 0.006 | 0.017 |
| L.VAR | 0.965 * | 0.009 | 0.863 * | 0.015 | 0.944 * | 0.011 | 0.965 * | 0.016 | 0.906 * | 0.019 | 0.943 * | 0.0155 |
| R2 | 0.976 | 0.926 | 0.965 | 0.902 | 0.881 | 0.918 | ||||||
| II. Fixed effects (416 obs.) | ||||||||||||
| INT | -9.449 * | 1.906 | 0.275 | 2.1953 | -1.857 | 2.271 | -20.857 * | 6.0594 | -29.648 * | 6.055 | -15.345 * | 4.1089 |
| INF | -0.049 | 0.013 | -0.090 * | 0.0211 | -0.078 * | 0.017 | 0.071 | 0.225 | 0.041 | 0.059 | -0.042 | 0.0385 |
| GOV | 0.380 * | 0.010 | 0.007 | 0.0769 | 0.345 * | 0.065 | 0.314 | 0.225 | 0.556 * | 0.208 | 0.382 * | 0.1327 |
| POP | 0.605 * | 0.007 | -0.127 | 0.1435 | 0.064 | 0.146 | 1.213 * | 0.3976 | 1.945 * | 0.398 | 0.948 * | 0.2681 |
| L.VAR | 0.568 * | 0.009 | 0.6366 * | 0.0278 | 0.695 * | 0.043 | 0.501 * | 0.0473 | 0.565 * | 0.042 | 0.559 * | 0.0458 |
| R2 | 0.612 | 0.855 | 0.868 | 0.364 | 0.327 | 0.427 | ||||||
| F | 2.86 * | 7.98 * | 2.74 * | 4.05 * | 2.97 * | 3.01 * | ||||||
| III. Random effects (416 obs.) | ||||||||||||
| INT | -0.288 ** | 0.119 | -1.028 * | 0.220 | -0.528 * | 0.155 | -0.970 *** | 0.5155 | -1.160 ** | 0.506 | -0.598 *** | 0.3241 |
| INF | -0.058 * | 0.013 | -0.042 *** | 0.024 | -0.070 * | 0.016 | -0.192 * | 0.0645 | -0.085 | 0.056 | -0.085 ** | 0.0365 |
| GOV | -0.003 | 0.010 | -0.016 | 0.018 | -0.003 | 0.012 | -0.051 | 0.048 | -0.105 * | 0.042 | -0.029 | 0.0273 |
| POP | 0.004 | 0.007 | 0.029 ** | 0.012 | 0.008 | 0.008 | 0.003 | 0.0295 | 0.023 | 0.027 | 0.006 | 0.0174 |
| L.VAR | 0.965 * | 0.009 | 0.863 * | 0.014 | 0.944 * | 0.011 | 0.965 * | 0.0165 | 0.906 * | 0.019 | 0.943 * | 0.0155 |
| R2 | 0.976 | 0.926 | 0.966 | 0.903 | 0.882 | 0.919 | ||||||
| Hausman A | 69.61 * | 32.7 * | 71-27 * | 119.20 * | 85.43 * | 19.65 * | ||||||
Source: Own elaboration.
Note: INT is the intercept, INF is the natural log of the inflation rate, GOV is the natural log of government spending, POP represents the natural log of population, and L.VAR is the lagged dependent variable. CRE, CON, HOU, SEC1, SEC2, and SEC3 are the bank credit variables. LR is the likelihood ratio. Hausman A refers to the Hausman test to decide between fixed and random effects. F stands for the F test. *, ** and *** indicate significance at 1, 5, and 10%, respectively. e.e. is the standard error.
In Panel II we present the estimations based on the fixed-effects technique. The inflation rate also has negative sign in most columns, with exception of the secondary sector which is insignificant. In essence, the coefficients of the inflation rate are statistically significant only for total loans, consumption loans, and mortgage loans with a range between -0.049 and -0.078. Moreover, R2 is high for consumption and mortgage and has an acceptable level for total loans. Finally, in all the regressions the statistically significant F test indicates that fixed effects are present in the estimations and rejects the null hypothesis that individual effects are zero. In Panel III, we show the random-effects regressions where the negative sign of prices increases dominates and the coefficients are significant in most instances. The Hausman test, which is significant in all regressions, points out the existence of correlation between individual effects and the explanatory variables. Thus, we should prefer the fixed-effects approach over random effects.
The dynamic panel data estimations appear in Table 5. The usefulness of these estimations is that we can distinguish short-run from long-run coefficients. In Panel IV of the mean group model with 384 observations, the sign of the inflation rate is inconsistent because it is positive in three long-run regressions. In the cases of consumption loans and the secondary sector, the size of the inflation rate is unrealistic. Regarding the short run and although the error correction term is statistically significant in all regressions, the inflationary effect continues to be erratic. In Panel V we present the estimations from the pooled mean group cointegration. It should be noted that the long-term sign of inflation rate behaves better than in the last estimation and it is significant as well. As before, the error correction term is negative and highly significant in all estimations. However, in this new set of regressions we added the Hausman test to explore whether there are significant differences between the three estimators. The null hypothesis of the Hausman test affirms that differences in the coefficients of MG and PMG or PMG and DFE are not systematic. If the null hypothesis is rejected, then we select PMG over MG and DFE over PMG. According to the values of the Hausman test shown at the bottom of Panel V, the pooled mean group is preferred over the mean group cointegration.
Table 5 Dynamic Panel Data Estimations of Inflation and Bank Credit: MG, PMG, and DFE Estimators.
| CRE | e.e | CON | e.e | HOU | e.e | SEC1 | e.e | SEC2 | e.e | SEC3 | E.E | |
| IV. Mean group (384 obs.) | ||||||||||||
| Long-run coefficients | ||||||||||||
| INF | -0.069 | 0.177 | -30.29 | 28.648 | 0.025 | 0.301 | 1.930 | 1.592 | -51.911 | 53.057 | 2.494 | 2.037 |
| GOV | 1.333 | 0.937 | -70.21 | 1.040 | -2.124 | 2.338 | 1.318 | 1.645 | -87.177 | 86.114 | -1.616 | 1.849 |
| POP | 1.585 | 1.044 | 4.862 | 1.700 | 2.820 | 1.359 | 0.833 | 4.358 | 7.880 | 5.050 | 7.146 ** | 3.408 |
| Short-run coefficients | ||||||||||||
| ECT | -0.630 * | 0.102 | -0.301 * | 0.033 | -0.447 * | 0.082 | -0.710 ** | 0.079 | -0.789 | 0.100 | -0.748 ** | 0.087 |
| ∆INF | -0.052 | 0.044 | 0.124 * | 0.042 | 0.003 | 0.047 | 0.185 | 0.156 | -0.039 | 0.116 | -0.022 | 0.093 |
| ∆GOV | 0.309 | 1.153 | 1.210 * | 0.204 | 0.478 * | 0.175 | 0.989 ** | 0.444 | 0.901 | 0.610 | -0.196 | 0.305 |
| ∆POP | -0.426 | 1.104 | -1.227 | 1.753 | 1.069 | 1.533 | 0.298 | 6.810 | 9.948 | 6.963 | -0.123 | 3.106 |
| INT | -32.913 * | 5.136 | -33.11 | 5.655 | -14.962 ** | 6.107 | -55.695 ** | 18.570 | -94.033 | 22.405 | -23.205 | 14.841 |
| V. Pooled mean group (384 obs.) | ||||||||||||
| Long-run coefficients | ||||||||||||
| INF | -0.399 * | 0.085 | -1.235 * | 0.129 | -0.701 * | 0.135 | -0.378 * | 0.123 | 0.192 | 0.138 | -0.049 | 0.063 |
| GOV | 0.084 | 0.131 | -2.892 * | 0.383 | 0.019 | 0.206 | -1.823 * | 0.375 | 0.785 * | 0.276 | 1.331 * | 0.115 |
| POP | 1.603 * | 0.184 | 0.449 | 0.441 | 0.444 | 0.395 | 6.810 * | 0.549 | 3.511 * | 0.467 | 3.241 * | 0.222 |
| Short-run coefficients | ||||||||||||
| ECT | -0.314 * | 0.032 | -0.274 * | 0.018 | -0.259 * | 0.021 | -0.512 * | 0.050 | -0.476 * | 0.049 | 0.533 * | 0.069 |
| ∆INF | 0.037 | 0.009 | 0.156 | 0.020 | 0.034 * | 0.011 | 0.096 *** | 0.054 | -0.027 | 0.057 | 0.067 *** | 0.035 |
| ∆GOV | 0.315 * | 0.079 | 0.672 * | 0.124 | 0.496 * | 0.098 | 1.639 * | 0.368 | 0.628 *** | 0.314 | 0.047 | 0.215 |
| ∆POP | 1. 686 * | 0.555 | -0.940 | 1.312 | 1.818 ** | 0.787 | 3.152 | 4.367 | 9.098 ** | 4.009 | 4.781 ** | 2.419 |
| INT | -8.452 * | 0.856 | -5.118 * | 0.370 | -3.331 * | 0.281 | -57.112 * | 5.491 | -26.162 * | 2.770 | -27.118 * | 3.585 |
| Hausman B | 4.49 | 6.23 | 6.23 | 1.84 | 1.69 | 1.12 | ||||||
| VI. Dynamic fixed effects (384 obs.) | ||||||||||||
| Long-run coefficients | ||||||||||||
| INF | -0.206 ** | 0.080 | -0.780 * | 0.123 | -0.418 * | 0.152 | -0.440 | 0.270 | 0.176 | 0.267 | -3.513 *** | 0.188 |
| GOV | 0.517 * | 0.151 | -0.401 *** | 0.231 | 0.471 *** | 0.258 | -0.639 | 0.557 | 0.415 | 0.536 | 0.422 | 0.349 |
| POP | 1.683 * | 0.243 | -0.382 | 0.979 | 0.494 | 0.524 | 3.650 * | 0.968 | 5.601 * | 0.900 | 2.468 * | 0.588 |
| Short-run coefficients | ||||||||||||
| ECT | -0.361 * | 0.049 | -0.364 * | 0.026 | -0.255 * | 0.45 | -0.474 * | 0.046 | -0.431 * | 0.041 | -0.424 * | 0.046 |
| ∆INF | 0.009 | 0.018 | 0.148 * | 0.026 | 0.009 | 0.022 | 0.077 | 0.086 | -0.061 | 0.078 | 0.064 | 0.051 |
| ∆GOV | 0.340 * | 0.064 | 0.500 * | 0.091 | 0.445 * | 0.077 | 1.458 * | 0.296 | 0.786 * | 0.269 | 0.481 * | 0.175 |
| ∆POP | 0.875 | 0.652 | -0.923 | 0.979 | 0.917 | 0.832 | 1.837 | 3.140 | 7.811 * | 2.853 | 4.889 * | 1.848 |
| INT | -9.728 * | 1.862 | -0.418 | 2.220 | -3.044 | 2.294 | -29.825 * | 6.383 | -37.229 * | 6.345 | -17.503 * | 4.281 |
| Hausman B | 0.00 | 0.04 | 0.01 | 0.16 | 0.06 | 0.23 | ||||||
Source: Own calculations.
Note: INT is the intercept, INF is the natural log of the inflation rate, GOV is the natural log of government spending, POP represents the natural log of population, and L.VAR is the lagged dependent variable. CRE, CON, HOU, SEC1, SEC2, and SEC3 are the bank credit variables. LR is the likelihood ratio. Hausman B refers to the Hausman test to decide between MG, PMG and DFE estimators. *, ** and *** indicate significance at 1, 5, and 10%, respectively. e.e. is the standard error.
In Panel VI we present the estimations based on the dynamic fixed effects technique. In all regressions, with exception of the secondary sector, the long-term coefficients of the inflation rate are negative and statistically significant (for the services sector the parameter is significant at 10%). Additionally, the error correction term is negative in all instances and highly significant at 1%. The Hausman test confirms that dynamic fixed effects should be chosen over the pooled mean group estimation. With respect to the short run, we should underline the positive and significant sign of the inflation rate. This deserves a further explanation, because it is possible that in the short run, economic agents require bank loans to meet some obligations, e.g., consumption needs of households and working capital in the case of firms. Nonetheless, in the long run bankers may realize that if the expected inflation rate is higher, economic agents will face financial distress with the ensuing problem of late or null repayments. Therefore, bankers would tend to reduce loans for the private sector.
In summary, with static and dynamic panel data models we have demonstrated the long-run adverse effects of prices increases on bank loans. Although it may seem contradictory, in the short run the banking system is willing to issue loans to help firms and households. In relation to the estimations, we detected the presence of fixed effects, static and dynamic, in our panel data of 32 Mexican states.
Discussion
We studied panel data of the 32 Mexican states over the period of 2003-2015 to understand the effects of inflation on private sector bank credit under an environment of macroeconomic stability. We disaggregated data by loan types (total credit, consumption credit, and mortgage credit) and loans to economic sectors (primary, secondary, and tertiary). We applied two sets of panel data techniques, such as traditional estimators including pooled OLS, fixed effects, random effects, and dynamic estimators like mean group, pooled mean group, and dynamic fixed effects.
The theory of finance and growth states that financial intermediaries influence on the level and rate of economic activity. If intermediaries carry out efficiently the functions of risk amelioration, resource allocation, corporate control, savings mobilization, and trading of goods and services, they could enhance investment productivity, technology, and the long-run economic growth. However, in practical terms, several factors tend to affect the degree of efficiency of financial institutions. As we saw, in our country banking intermediation is regionally concentrated regarding branches, credit card accounts, and private sector loans (mainly in Ciudad de México and Estado de México). Also, the access to bank credit is low because only 10% of people that received loans used formal financial institutions and 27% of small and medium-sized firms had bank financing. Moreover, the actual and expected rate of inflation rate could be particularly harmful because it could distort the decision-making process of bank executives to finance more efficient investment projects.
In line with most empirical studies, our main findings indicate that in the long run inflation rates exert negative effects on bank credit, but in the short run those effects tend to be positive. In the pooled OLS, fixed effects and random effects estimations, the inflation rate had a negative sign which confirms the expected sign of an inverse relationship between loans and price changes. Based on the fixed-effects technique, a negative relationship was found to be significant only for total loans, consumption loans, and mortgage loans with coefficients ranging from -0.08 and -0.05. On the other hand, the advantage of adding dynamic estimators in our research is that we can calculate short and long-run coefficients. According to our preferred estimator, i.e., dynamic fixed effects, in the short run we found that price changes exert a positive effect on bank credit, although in the long run the relationship is negative-it was insignificant in the case of the secondary sector. One possible explanation is that households and firms do not face constraints in obtaining short-term loans, but bank executives are more careful when granting long-term credit if expected inflation is higher.
The results obtained in this study are important for policymakers. In developing economies like Mexico, monetary authorities should still concentrate their efforts in controlling the inflation rate to ensure a stable macroeconomic environment where economic agents make decisions under certainty while at the same time avoid unnecessary risks. Under such environment, the banking system could operate efficiently and allocate resources to the best entrepreneurs, and borrowers in general, that offer the highest returns. In addition, the authorities should introduce adequate regulations to monitor the quality of loans to avoid high delinquency rates and maintain a healthy financial system.
Based on this research, one venue of research could study the specific channels through which inflation affects the level of bank credit because here we could only quantify the negative relationship between inflation rates and bank credit. An additional venue could focus on understanding the causes of low access and credit in most Mexican states. A related point would be to examine the role of government financial policies towards offering banking services in less developed states.











 nueva página del texto (beta)
nueva página del texto (beta)



