1. Introducción
Investigaciones previas indican las dificultades que tienen los estudiantes en la comprensión de las figuras geométricas (Battista, 2007; Clements, Swaminathan, Hannibal & Sarama, 1999; Verdine, Lucca, Golinkoff, Hirsh-Pasek & Newcombe, 2016; Walcott, Mohr & Kastberg, 2009). Dicha comprensión se apoya en las acciones mentales que se generan cuando los alumnos realizan alguna acción con las figuras, reconociendo sus atributos, estableciendo relaciones entre ellos y generando clasificaciones (Battista, 2007). Los niños desde pequeños aprenden a nombrar las figuras más comunes sin llegar a usar los atributos y propiedades que las definen (Clements et al., 1999; Fisher et al., 2013; Satlow & Newcombe, 1998), creándose modelos de imágenes que organizan sus acciones. Estas imágenes se encuentran vinculadas a figuras prototípicas y presentan una fuerte característica visual (Hershkowitz et al., 1990; Moriena y Scaglia, 2003; Scaglia y Moriena, 2005). Sin embargo, el uso de los atributos para razonar sobre las figuras permite a los niños superar la influencia de las figuras prototípicas, pudiendo prestar atención a determinados atributos comunes con el propósito de generar sus definiciones. Por ejemplo, para reconocer triángulos con posiciones diferentes a las usuales (Hannibal, 1999; Levenson, Tirosh & Psamir, 2011; Satlow & Newcombe, 1998; Vinner y Hershkowitz, 1983; Yesil-Dagli & Halat, 2016), o usar la diferencia entre la longitud de los lados para separar los cuadrados de los rectángulos (Halat & Yesil-Dagli, 2016; Yesil-Dagli & Halat, 2016). En este sentido, es necesario generar una relación significativa entre la definición, como conjunto mínimo de atributos, y las imágenes perceptuales, procedentes de representaciones gráficas prototípicas, para dar sentido de pertenencia a una clase. La manera en la que los niños dotan de sentido a las diferentes clases de figuras supone una evolución de lo concreto a lo abstracto, al poder generarse categorías de figuras. Es decir, desde el dibujo como representación gráfica de una figura y la figura como referente teórico (Moriena y Scaglia, 2003). Estos resultados preliminares indican que reconocer y analizar los atributos de las figuras es necesario como un paso previo al de generar relaciones entre dichos atributos para construir el significado de “clase de figura”.
Sin embargo, tenemos información limitada sobre la transición, desde el reconocimiento de los atributos de las figuras hasta comprender las figuras cuando pertenecen a clases de figuras (Siew, 2003). El análisis de las características que determinan esta transición en niños de 6 a 9 años define el problema de investigación que abordamos en este trabajo.
2. Marco teórico
La manera como los niños construyen la representación del espacio es un proceso vinculado a las acciones de reconocer atributos en las figuras y establecer relaciones entre ellos para clasificarlas (Holloway, 1982). En general, la transición de lo perceptual a lo conceptual en el desarrollo del razonamiento geométrico ha sido abordada desde diferentes perspectivas teóricas que intentan dar cuenta de la transición entre el reconocimiento perceptual, el análisis y la clasificación de figuras (Clements et al., 1999; Clements y Battista, 1992; Sinclaire et al., 2016). En esta investigación, para examinar este desarrollo en el caso particular del proceso de dotar de sentido a clases de figuras en niños de 6 a 9 años, nos apoyamos en las aprehensiones descritas por Duval (1995, 1999). La aprehensión perceptual es la capacidad que tiene un individuo para reconocer o percibir en un plano o en profundidad las figuras, aparte de ser capaz de nombrar figuras y reconocerlas dentro de un subconjunto; la aprehensión discursiva es la capacidad de vincular hechos geométricos a las figuras, y de realizar declaraciones sobre la denominación, definición y reconocimiento de las propiedades geométricas, entre otras; y la aprehensión operativa es la capacidad de modificar una figura para resolver problemas geométricos, lo cual incluye cambiar su posición u orientación.
La relación entre estas aprehensiones está en la base del aprendizaje de la geometría y del desarrollo del pensamiento geométrico, que permite asumir el vínculo entre las imágenes perceptuales y los atributos teóricos que definen la inclusión de la figura en una clase, considerando la idea de concepto figural (Fischbein, 1993). Por ejemplo, un cuadrado es un concepto definido formalmente como un paralelogramo con lados y ángulos consecutivos congruentes, pero desde un punto de vista perceptual refleja aspectos relativos a la posición y tamaño que deben limitarse por los aspectos formales de la definición. Sin embargo, las imágenes perceptuales y las propiedades de las figuras interactúan en la actividad cognitiva de una persona, pudiendo crear conflictos en el desarrollo del concepto figural (Fisher, Hirsh-Pasek, Newcombe & Golinkoff, 2013; Gagatsis et al., 2010; Yesil-Dagli y Halat, 2016). Particularmente, en este proceso, Duval subraya la relevancia de las relaciones entre la capacidad de reconocer, modificar, construir o describir las figuras y asignarles hechos o propiedades geométricas. Es decir, la comprensión de las figuras debe desarrollarse de manera que el reconocimiento perceptual dé paso a una comprensión conceptual apoyada en el reconocimiento y asociación de atributos y propiedades geométricas. Desde estas referencias previas, generamos el siguiente objetivo de investigación:
Identificar características de la progresión, desde el reconocimiento perceptual a la comprensión conceptual que define la comprensión de las figuras geométricas en estudiantes de 6 a 9 años.
3. Método
3.1. Participantes y contexto curricular
Participaron 30 niños (19 chicos y 11 chicas) de educación primaria, entre 6-9 años de edad (Tabla 1). Los alumnos proceden de una escuela pública y fueron escogidos por sus maestros considerando diferentes rendimientos académicos y su capacidad de comunicación. El currículo de las figuras geométricas que cursaban estos niños se organiza a través del reconocimiento y construcción de las mismas; reconocer diferentes atributos (concavidad/convexidad, número de lados, tipos de triángulos, tipos de cuadriláteros); construcción mediante la composición y descomposición de figuras; y la realización de clasificaciones siguiendo algún criterio. El desarrollo de las acciones mentales de reconocer (aprehensión perceptual/operativa) y relacionar atributos para clasificar (aprehensión discursiva/operativa) se apoya en la generación de un vocabulario específico y en el uso de determinados instrumentos (geoplanos, trama de puntos, plantillas, reglas, semicírculos, espejos, programas informáticos de geometría dinámica) de manera gradual a lo largo de la educación primaria.
3.2 Entrevista y procedimiento
Los datos se recogieron mediante entrevistas clínicas. Las tareas fueron diseñadas y/o adaptadas de investigaciones previas (Clements et al., 1999; Sarama y Clements, 2009) y su objetivo era identificar características de cómo los niños reconocen atributos de las figuras y cómo llegan a considerarlas como ejemplos de clases más amplias. En las tareas se pretendía que se combinaran las aprehensiones perceptual/operativa y discursiva/operativa, ya que en el reconocimiento de las figuras y de los atributos geométricos se pueden apoyar en la aprehensión operativa (Tabla 2).
Tabla 2 Relación entre las actividades en el guion de la entrevista, las acciones pretendidas y las aprehensiones descritas por Duval.

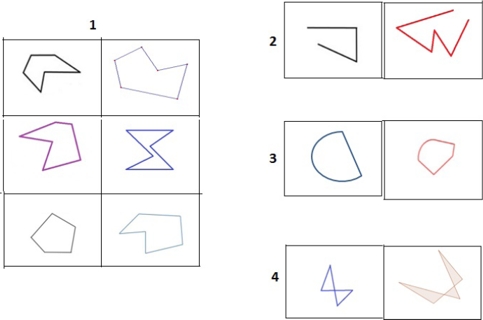
Para hacer las entrevistas usamos un conjunto de figuras geométricas representadas en tarjetas (Figura 1) (Martin, Lukong & Reaves, 2007; Tsamir, Tirosh & Levenson, 2008). Las figuras utilizadas variaban en varios atributos (lados rectos/curvos; figuras cerradas/abiertas, figuras cruzadas/no cruzadas, polígonos y no polígonos, y cóncavos/convexos) que representaban ejemplos prototípicos de figuras, ejemplos poco familiares y contraejemplos de polígonos, variando diferentes atributos que los definen. El guion de la entrevista clínica era el mismo para todos los cursos, excepto para los niños de primer curso, que no hicieron las tareas relativas a reconocer atributos de los triángulos (longitud de los lados y amplitud de los ángulos), por no estar incluidas en el currículo de ese curso. Usamos el formato de una entrevista basada en tareas (Goldin, 2000), definiendo un contexto que facilitaba el que los estudiantes hablaran y/o explicaran cómo resolvían las actividades. Las actividades en la entrevista implican generar aprehensiones perceptual (reconocer diferencias entre figuras), operativa (poder mover las figuras para justificar el reconocimiento de algún atributo) y discursiva (asociar términos geométricos a las figuras). En esta investigación no consideramos la realización de las actividades de construir, por lo que la aprehensión secuencial (capacidad para construir o describir la construcción de una figura) no fue considerada.
El guion de la entrevista estaba formado por 17 actividades (Tabla 2). Diseñamos 9 actividades de reconocer atributos y diferencias entre figuras, reconocer una figura dado un listado de atributos y reconocer polígonos/no polígonos. Por otra parte, diseñamos 8 actividades de clasificar, en 6 de ellas se pedía clasificar un grupo de figuras (primero de manera libre y luego proporcionando el entrevistador un criterio) y 2 actividades en las que se pedía clasificar un grupo de polígonos considerando dos criterios simultáneamente.
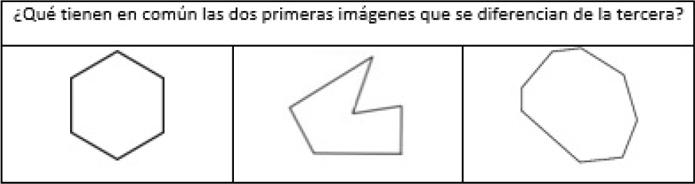
Las figuras usadas en las actividades de reconocer atributos variaban en cinco atributos: lados rectos o curvos, figuras cerradas o abiertas, cruzadas o no cruzadas, el número de lados (de tres a nueve) y figuras cóncavas/convexas. En el primer tipo de las actividades de reconocer se presentaba a los niños dos figuras que compartían un atributo, junto a una tercera que no lo tenía, y se preguntaba: ¿Qué tienen en común las dos primeras figuras que se diferencia de la tercera? (Tabla 3). En un segundo tipo de actividad se proporcionaba un listado de atributos de manera verbal y cuatro figuras, y los alumnos debían reconocer la figura que los cumplía. Finalmente, en el tercer tipo de actividades de reconocer, y una vez dada la definición de polígono, los niños debían reconocer polígonos y no polígonos en un conjunto de figuras. El objetivo de estas actividades era identificar cómo los estudiantes reconocían atributos diferentes en las representaciones. Para los sujetos de segundo y tercer curso se plantearon actividades adicionales centradas en las diferencias entre triángulos considerando la longitud de los lados (triángulo equilátero, isósceles o escaleno) y la medida de los ángulos internos (triángulo acutángulo, rectángulo u obtusángulo).
En las tareas de clasificar consideramos dos versiones. Una en la que los niños debían agrupar de manera libre, generando sus propios criterios (Tabla 4), y otra tarea en la que se daba un criterio o varios criterios (Figuras 4a y 4b). En estas últimas tareas se proporcionaba una cuadrícula con dos criterios y un grupo de figuras, y los alumnos debían clasificar las figuras en la cuadrícula.
Tabla 4 Estructura del guion de la entrevista basada en tareas de Agrupar (sin proporcionar criterio).
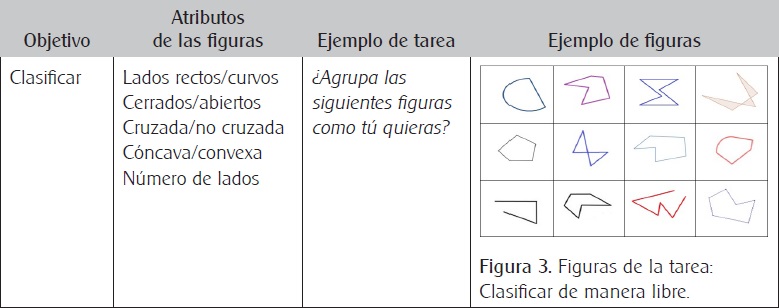

Figura 4b Cuadrícula de doble entrada proporcionada para clasificar las figuras considerando dos criterios: el número de lados y la concavidad/convexidad.
Las entrevistas tuvieron una duración aproximada de 45 minutos. El guion de la entrevista se fue adaptando, según las respuestas dadas por los niños. Si el niño parecía confuso o no entendía la tarea, la entrevistadora repetía la pregunta o modificaba la tarea. Por ejemplo, en las tareas de reconocer atributos, si algún niño no veía diferencias entre las tres figuras proporcionadas (dos figuras que compartían un atributo y la tercera con uno diferente), se escogía una figura de las que compartían atributo y la figura que no lo tenía, y se le preguntaba por las diferencias entre las dos figuras, con el propósito de que los niños pudieran generar varias posibles diferencias. La entrevistadora siempre preguntaba el porqué de sus respuestas. Los datos de esta investigación están constituidos por las transcripciones de las grabaciones en video de las entrevistas y las notas tomadas por la entrevistadora al finalizar cada entrevista.
3.3. Análisis
En las trascripciones de las entrevistas cada participante fue identificado con la palabra N para indicar niño, seguido de un número del 1 al 3 para indicar el curso y, a continuación, un número del 1 al 10 indicando el número del participante de dicho curso. Por ejemplo, el alumno N1-3 significa que es el niño 3 de primer curso.
El análisis siguió los pasos descritos por Clement (2000) para generar descriptores y categorías de observación inductivamente, centrándonos en lo que podían ser evidencias de la manera de pensar de los estudiantes. Para esto, se visionaban los videos de las entrevistas para reconocer las diferentes formas de proceder de los niños en cada tarea, y se leyeron las transcripciones para identificar las razones dadas por ellos en sus respuestas. Así, para cada niño describimos la manera en la que resolvía cada tarea considerando las aprehensiones que ponía en práctica (perceptual, discursiva y operativa), y los atributos considerados (número de lados, concavidad/convexidad, figuras cerradas/abiertas, lados rectos/curvos, y/o cualquier otra diferencia que mencionaba). A continuación, generamos una inferencia de lo que parecía significar la conducta del niño desde la perspectiva del reconocimiento de diferentes atributos de las figuras y cómo las agrupaba.
Los códigos generados fueron asociados con los mecanismos cognitivos referidos a las aprehensiones perceptual, discursiva y operativa, considerando los atributos de las figuras mencionados por los alumnos (Tabla 5). A partir de estos códigos generamos categorías explicativas del proceder de los niños. Estas características son las que describiremos en la sección de resultados.
4. Resultados
Los resultados indican la ampliación progresiva de los significados asociados con los términos usados (el dominio semántico de las palabras) para referirse a las figuras y sus atributos, que puede estar relacionada con la experiencia escolar (enseñanza y currículo). Sin embargo, un aspecto característico es que esta ampliación de los significados asociados con los términos geométricos está relacionada con el papel desempeñado por las figuras prototípicas y la relación entre la aprehensión perceptual y discursiva. Esto se puede apreciar en la Tabla 6, donde se relacionan a) Las actividades (reconocer y clasificar) y b) Los cursos (niños de 6 a 9 años).
En relación a las actividades de reconocer atributos de las figuras de manera aislada, los estudiantes reconocieron en primero con más facilidad las figuras abiertas/cerradas, siendo el atributo más difícil de reconocer inicialmente los lados rectos/curvos. Sin embargo, en tercero ya reconocían con bastante facilidad los diferentes atributos de las figuras cuando se les pedía de manera aislada (lados curvos/rectos, figuras abiertas/cerradas, y cuando había una figura cruzada). Si los niños tenían que reconocer figuras que cumplían una serie de atributos, en primero y segundo cometían errores, mostrando cierta limitación en su capacidad para considerarlos de manera simultánea. Sin embargo, en tercero ya pueden usar listados de atributos de manera simultánea para reconocer figuras. Esta capacidad es relevante para determinar la manera en la que los alumnos pueden llegar a reconocer cuando una figura es o no un polígono (figura cerrada, lados rectos y no cruzada). En este sentido, hay una evolución positiva de primero a tercero, al considerar simultáneamente varios atributos para reconocer las figuras.
Considerando los atributos de los polígonos, reconocer cuando eran cóncavos o convexos resultó difícil para los niños, y no hubo casi evolución en el reconocimiento de este atributo a lo largo de los tres años. También fue difícil reconocer el número de lados si era elevado. En el caso particular de los triángulos, para los cursos de segundo y tercero, considerar la longitud de los lados evolucionó claramente entre estos dos cursos, sin embargo, no identificamos evolución en la manera en la que reconocían la amplitud de los ángulos.
En cuanto a las actividades de clasificar siguiendo un criterio de manera libre, clasificaron con bastante éxito desde primero cuando usaban el criterio de polígono/no polígono y separando triángulos y cuadriláteros, sin embargo, no hubo casi evolución cuando decidían agrupar considerando el número de lados, ya que al aumentar el número de lados de los polígonos se les dificultaba clasificar alguna figura (colocando polígonos en grupos que no cumplían el criterio). Cuando consideraban como criterio para clasificar polígonos si eran convexos o cóncavos, en primero tuvieron dificultades, particularmente con determinadas figuras, aunque esta capacidad fue mejorando hasta llegar a tercero.
En el caso de los triángulos, de segundo a tercero mejoró la capacidad de clasificar considerando la longitud de lados, pero si querían considerar la amplitud de los ángulos, seguían cometiendo errores. Este hecho muestra la diferencia entre reconocer y clasificar usando longitud de lados y/o amplitud de los ángulos. Como consecuencia de este hecho, no realizaron con éxito las actividades de clasificar triángulos en las que tenían que considerar estos dos atributos de manera simultánea.
El entrevistador propuso actividades de clasificar siguiendo algún criterio que los alumnos no habían usado de manera libre previamente. Estas actividades adicionales mostraron la evolución de la capacidad de clasificar polígonos y no polígonos y clasificar triángulos y cuadriláteros. Sin embargo, las tareas de considerar diferentes números de lados para clasificar los polígonos, resultaron bastante difíciles en los dos primeros cursos (vinculadas a la dificultad de considerar polígonos con un número elevado de lados) aunque mejoraron en tercero, mostrando su evolución al considerar el número de lados para clasificar.
Por último, la dificultad de reconocer los polígonos cóncavos/convexos identificada inicialmente, se puso de manifiesto en las tareas de clasificar en las que no hubo casi mejora a lo largo de los tres años, pero sí identificamos una evolución en el uso de dos criterios para clasificar (número de lados y concavidad), vinculada a la evolución en el reconocimiento de dichos atributos y a considerarlos simultáneamente en una figura.
Estos resultados definen dos ámbitos que aportan información que nos ayuda a comprender la progresión desde el reconocimiento perceptual de las figuras hasta su comprensión conceptual en los niños de 6 a 9 años: (i) La influencia de lo perceptual en la generación del concepto figural evidenciado en la actividad de reconocer figura, y (ii) La manera en la que los estudiantes de 6 a 9 años consideran las figuras como elementos de una clase.
4.1. Sobre el reconocimiento de las figuras
El reconocimiento de las figuras refleja la influencia de lo perceptual a través del uso del lenguaje: la comparación con objetos de la vida real (aprehensiones perceptuales) y la invención de términos para referirse a determinados atributos de las figuras, indicación de que se reconoce el atributo, aunque no se conozcan los términos específicos para nombrarlo. Por ejemplo,
INV: ¿En qué se parecen estas dos figuras que se diferencian de esta?
N1-3: Porque estas dos no tienen ninguna línea cruzada (izquierda) y esta hace como un reloj de arena (derecha).
Cuando no conocen los términos específicos, los niños usan un vocabulario particular para nombrar los atributos que reconocen, con artículos demostrativos como esto o eso para indicar la diferencia en las figuras, evidenciando el reconocimiento perceptual del atributo, al mismo tiempo que el desconocimiento de la palabra para expresarlo. Por ejemplo, para diferenciar las figuras cerradas/abiertas indican que las figuras abiertas “no están hechas”, y para diferenciar las figuras cóncavas de las convexas, usan la palabra “picos” al referirse a los vértices que emergen de la concavidad. Así, en la tarea ¿en qué se parecen esas dos (figuras de la izquierda) que se diferencian de esa (figura de la derecha)?, indicaban
N1-6: Que estas tienen picos (señalando las dos figuras de la izquierda) y esta no (la figura de la derecha).
INV: ¿A qué te refieres con picos?
N1-6: Pues a esto y esto (señalando los picos que emergen de la concavidad de los polígonos cóncavos).
Esta característica es matizada cuando se conocen los términos adecuados. Así dejan de usar expresiones como “(no) está hecha”, para reconocer las figuras como cerradas o abiertas, aportando explicaciones más elaboradas. No obstante, la progresión en el uso de los términos no es uniforme para todos los atributos considerados. Por otra parte, los términos para referirse a la concavidad y convexidad de los polígonos son más difíciles, por lo que los niños usan las palabras picos, bocas o está abierta para referirse a los lados y ángulos que muestran la concavidad del polígono.
Además, los resultados indican que la mayoría de los niños son capaces de reconocer diferencias entre figuras usando los atributos más allá de solo reconocer la semejanza perceptual, pero que esta capacidad depende de los atributos considerados. Por ejemplo, los atributos inicialmente reconocidos son los lados rectos/curvos, y las figuras abiertas/cerradas. Por el contrario, presentan dificultades en reconocer las figuras cuando el número de lados es grande, las figuras tienen lados cruzados y son cóncavas. Por otra parte, cuando el número de lados es grande confunden los polígonos convexos de muchos lados con círculos o figuras con lados curvos. Como en el caso de la tarea en la cual tienen que reconocer el número de lados como el atributo que diferencia una figura en relación a las otras dos, indican
INV: ¿En qué se parecen estas dos (mostrando las dos figuras de la izquierda), que se diferencian de esa? (indicando la figura de la derecha).
N1-10: Esto es un polígono (primera), esta también (segunda) y esta no (tercera) porque está curvo.
La dificultad en reconocer el número de lados como un atributo para diferenciar polígonos desaparece cuando se desarrolla la habilidad para contar el número de lados, y llegan a reconocer que una diferencia entre los polígonos es el número de lados.
En el caso particular de los triángulos, el rol desempeñado por la figura prototípica, dada por un triángulo equilátero, es más evidente pues usan tanto atributos relevantes para diferenciar los triángulos (longitud de los lados) como atributos no relevantes (la posición respecto al filo del papel). Además, aunque los niños pueden conocer los nombres de los diferentes triángulos, utilizan la imagen prototípica del triángulo equilátero como referencia para reconocer los otros triángulos, mostrando la influencia de lo perceptual para reconocer las diferencias entre los triángulos.
INV: ¿En qué se parecen estos dos triángulos que se diferencian de este?
N3-4: Pues que estos triángulos son “triángulos triángulos” (izquierda) y este no se parece tanto (derecha).
Esta actividad estaba dirigida a determinar cómo los estudiantes percibían las posibles diferencias en las representaciones de los triángulos. La manera de expresarse de los niños parece indicar que usan una referencia determinada como “representación del triángulo”. Esta actividad presentaba dos triángulos equiláteros con posición diferente, y un triángulo isósceles (con dos lados iguales y uno desigual) en una posición prototípica (el lado pequeño paralelo al filo de la cartulina). El discurso generado por los niños, aunque no exprese correctamente las diferencias, pone de manifiesto cómo la aprehensión perceptual se empieza a particularizar reconociendo atributos específicos.
4.2. Las figuras geométricas como elementos de clases
Identificamos dos características del pensamiento de los niños, relacionadas con el lenguaje y la manera en la que usan los atributos para clasificar, que evidencian el significado dado a las figuras como elementos de clases de figuras. El conocimiento de los términos para referirse a las figuras y sus atributos se refleja en forma en la que justifican las tareas de clasificar. Inicialmente describen los grupos según sus características perceptuales.
Tarea: Se le proporcionan 12 figuras diferentes y se le pide que las clasifique de forma libre.
N1-4 realiza dos grupos, “casi todos” los convexos (en la parte superior) y los cóncavos (en la parte inferior).
INV: ¿Por qué has agrupado así?
N1-4: He agrupado las que se parecen más a un círculo en un sitio (arriba) y las que más se parecen a triángulos o a cuadrados o figuras raras como esta (señalando el eneágono cóncavo) en otro sitio (abajo).
La manera en la que los niños realizan las actividades de clasificar muestra la transición desde lo perceptual (porque se parecen) al uso de diferentes atributos (lo analítico), aunque en un primer momento no conozcan los términos para nombrarlo. Por ejemplo, cuando se les pide clasificar de forma libre 12 figuras diferentes, N3-2 hizo cuatro grupos, indicando lo siguiente:
INV: ¿Cómo los has agrupado?
N3-2: En polígonos cerrados (1), las formas que son con líneas abiertas (2), las que tengan una línea curva (3) y las formas que son secantes (4).
En las actividades de clasificar triángulos se pone de manifiesto el papel desempeñado por las figuras prototípicas. Así, ante un grupo de triángulos diferentes, los niños consideraban triángulos a los equiláteros y algunos isósceles, y como no triángulos a algunos isósceles y escalenos, puesto que no son los típicos triángulos con los que se suelen encontrar:
INV: Vale, explícame, ¿por qué los has agrupado así?
N2-9: Porque estas se parecen más a un triángulo (izquierda) y aquí no se parecen (derecha).
En el caso particular de los triángulos y considerando la longitud de los lados, agrupan aquellos que tienen lados iguales o casi iguales y los que poseen un lado diferente a los otros dos,
INV: ¿Por qué has agrupado así?
N2-2: Porque estas tienen las líneas más largas (derecha) y estas las tienen cortas (izquierda).
En lo que respecta a los tipos de triángulos según sus ángulos, los alumnos manipulan las tarjetas colocando las bases de los triángulos paralelas al filo de la mesa, para visualizar mejor la figura y comparar los ángulos de los triángulos con el pico de la mesa, el ángulo de referencia de 90°. Los niños de tercero usan de manera más clara alguno de los atributos de las figuras para justificar las clasificaciones realizadas:
INV: Vale, explícame, ¿por qué has agrupado así?
N3-10: Los que tienen segmentos iguales, estos que tienen nueve segmentos los he puesto juntos (1), estos tienen cinco segmentos los he puesto juntos (2), este que tiene diez segmentos como no hay ninguna más que tiene diez segmentos la he puesto sola (3), esta que tiene tres segmentos la he puesto sola porque no hay ninguna más de tres segmentos (4), esta de ocho segmentos no la he puesto con ninguna porque tampoco tenía pareja (5), y esta de siete segmentos tampoco había otro de siete segmentos y se ha quedado sola (6).
N3-10 usa como criterio el número de lados.
Una característica relevante que ayuda a definir la progresión en la comprensión de las figuras geométricas como parte de una familia de figuras es que el éxito en las tareas de clasificar siguiendo los criterios dados depende del atributo y del reconocimiento de algunas de las figuras prototípicas. Por ejemplo, en el uso del atributo “cóncavo/convexo” inicialmente los niños incluyen algunas figuras cóncavas en el grupo de los convexos y viceversa, lo que muestra su dificultad en reconocer el atributo de concavidad para realizar las clasificaciones. En este caso, las figuras que plantean más dificultades son la flecha y la estrella, que son incorporadas al grupo de las figuras convexas.
Tarea: Se le proporcionan 12 figuras diferentes y se le pide que agrupe en cóncavos y convexos.
N1-6 agrupa en polígonos cóncavos y convexos, aunque no use esa terminología.
INV: Vale, explícame, ¿por qué has agrupado así?
N1-6: He hecho aquí las que tienen pico para fuera y para dentro (izquierda) y aquí las que tienen picos para fuera (derecha).
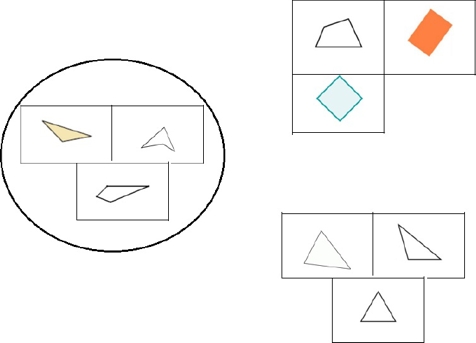
Por otra parte, a los niños les resulta difícil clasificar figuras no prototípicas, como en el caso de los cuadriláteros cóncavos, la cometa u otras figuras que son diferentes al cuadrado, rectángulo o triángulo equilátero. Un claro ejemplo de esta confusión generada por las figuras prototípicas vinculadas al uso de las palabras “triángulo” y cuadrilátero” se muestra en la tarea en la que se proporcionan 9 figuras formadas por cuadriláteros y triángulos, y se pide que clasifiquen en cuadriláteros y triángulos.
INV: Vale, te he pedido que hicieras dos grupos, uno de cuadriláteros y otro de triángulos, y yo veo tres grupos…
N1-10: Ya, si estas no cuentan (señalando el grupo de tres figuras que representan la cometa, el triángulo obtusángulo sombreado y el cuadrilátero cóncavo).
INV: Vale, estas no van a ningún sitio, están fuera. Entonces, explícame, aquí me has agrupado…
N1-10: Por triángulos (el grupo de abajo), aquí por cuadriláteros (grupo de arriba).
Esta respuesta indica que los niños asocian las palabras “triángulo” y cuadrilátero” con determinadas figuras, pero no usan los conceptos (triángulo: figura plana cerrada formada por tres lados rectos; cuadrilátero: figura plana cerrada formada por cuadro lados rectos) para realizar las clasificaciones.
5. Discusión y conclusiones
El objetivo de este estudio es identificar características de la progresión en la comprensión de las figuras en estudiantes de 6 a 9 años, considerando cómo reconocen y usan los atributos de las figuras para clasificarlas. Los resultados indican tres características relevantes del proceso de categorización de las figuras geométricas. En primer lugar, la existencia de un desfase entre el uso de los nombres de las figuras prototípicas y su comprensión conceptual; en segundo lugar, que reconocer y usar los atributos para clasificar las figuras no es un proceso uniforme y depende el atributo considerado; y finalmente, la influencia que desempeñan algunas figuras prototípicas —y el dominio semántico restringido del término usado para nombrarlas— en el proceso de reconocerlas y clasificarlas. Estas características informan del desarrollo que se inicia al apoyarse en semejanzas perceptuales, hasta usar propiedades conceptuales que dependen de las figuras prototípicas y de los atributos considerados.
5.1 La relación entre lo perceptual y lo discursivo
El tipo de atributo que centra la atención de los niños impone condiciones en su reconocimiento. La ampliación del reconocimiento de diferentes atributos define la progresión de la capacidad de reconocer y clasificar las figuras siguiendo un criterio. Esta característica de la progresión de la comprensión de las figuras indica que la perspectiva perceptual se va complementando con el uso de los atributos aportados por la definición. En el mismo sentido, este resultado está en línea con otras investigaciones llevadas a cabo con niños de educación infantil (de 3 a 6 años) que indican la complementariedad paulatina de la perspectiva perceptual en el reconocimiento de diferentes figuras con el razonamiento apoyado en el uso de algunos atributos (Clements et al., 1999; Fisher et al., 2013; Halat, y Yesil-Dagli, 2016; Satlow & Newcombe, 1998; Vinner y Hershkowitz, 1983; Yesil-Dagli, y Halat, 2016). Este proceso de complementar lo perceptual con lo conceptual en la comprensión de las figuras planas viene mediado por el uso de las figuras prototípicas y el uso de un lenguaje adecuado que evidencia el papel desempeñado por las aprehensiones discursivas en dar sentido a las figuras como elementos de una clase.
Nuestros datos también indican que el uso de los atributos para considerar si una determinada figura pertenece o no a una clase no fue uniforme para todos los atributos considerados en esta investigación (número de lados, lados rectos o no, concavidad/convexidad, polígonos/no polígonos). Este hecho indica que la comprensión de una determinada figura como perteneciente a una clase de figuras es progresiva y se va construyendo paulatinamente, incorporando el uso de diferentes atributos. En esta progresión, los niños pueden considerar al mismo tiempo ejemplos prototípicos y razonar con diferentes atributos que definen un grupo de figuras al clasificarlas. Este resultado, en línea con otras investigaciones efectuadas con alumnos de educación infantil (Clements et al., 1999), indica que los niños empiezan clasificando por semejanza perceptual y luego aportaban el criterio desde una perspectiva analítica, o aplicando de manera progresiva varios criterios y terminando con un grupo al que consideran que no pueden aplicar ningún criterio.
En la comprensión de una figura como ejemplo de una clase, nuestros resultados subrayan el papel desempeñado por las figuras prototípicas y el lenguaje vinculado (Mesquita, 1998; Verdine et al., 2016). Por ejemplo, el uso de las palabras “triángulo”, “polígono”, y “cuadrilátero” está inicialmente vinculado a determinadas figuras prototípicas, lo cual genera dificultades en el uso de los atributos dados por la definición para reconocer algunos triángulos o polígonos como ejemplos de una clase de figura más amplia (Clements et al., 1999; Fisher et al., 2013; Satlow & Newcombe, 1998). De tal manera, parece que las figuras prototípicas limitan el desarrollo de la comprensión de clases de figuras como una categoría en el pensamiento de los niños (Halat & Yesil-Dagli, 2016; Yesil-Dagli & Halat, 2016). Este resultado indica que las aprehensiones discursivas son el mecanismo cognitivo sobre el cual se construyen las tareas de clasificar que ayudan a generar el significado de concepto figural para cada figura (Duval, 1995, 1999; Mesquita, 1998; Verdine et al., 2016). Por ejemplo, un niño puede mover y cambiar de posición un polígono convexo de 5 lados para reconocerlo, pero además debe ser capaz de reconocer la diferencia con un polígono cóncavo de 5 lados no solo a nivel perceptual, sino por la diferencia en la convexidad. Así, podemos interpretar estos resultados en el sentido de que el desarrollo de la comprensión de las figuras geométricas, como ejemplos de clases de figuras, depende de la manera en la que se relacionan la figura prototípica y los diferentes atributos. De este modo, como indican Clements y sus colegas (1999), sería necesario el uso de redes de características y la introducción de conocimiento declarativo (por ejemplo, el conocimiento de los términos vinculados a las diferentes clases de figuras) para que los estudiantes aumenten la comprensión de las figuras geométricas.
5.2 Implicaciones para futuras investigaciones y la enseñanza
Nuestros resultados aportan información detallada de la manera en la que las aprehensiones discursivas se relacionan con las figuras prototípicas que señalan puntos de referencia a considerar en la enseñanza de la geometría durante los 6 a 9 años de edad. En este sentido, nuestros resultados permiten organizar la planificación de la enseñanza dirigida a que los niños lleguen a reconocer de manera consciente los diferentes atributos de las figuras para considerarlas pertenecientes a una determinada clase. La planificación de la enseñanza con este objetivo debe incorporar que los estudiantes puedan gradualmente ampliar el significado dado a expresiones verbales, como “triangulo”, cuadrado”, “paralelogramo” y así. Para ello, los maestros deberían alentar a los estudiantes a describir porqué una figura pertenece o no a un determinado grupo, como una forma de animarlos a completar sus descripciones perceptuales con el uso de atributos que definen a las figuras (Fisher et al., 2013; Gagatsis et al., 2010; Levenson et al., 2011; Yesil-Dagli y Halat, 2016). Por otra parte, los resultados de esta investigación dejan abiertas cuestiones relativas a la posible jerarquización de los diferentes atributos para dar sentido a la idea de clase de figura, y cómo es posible relacionar las características de la manera en la que los alumnos de 6 a 9 años de edad comprenden las figuras geométricas con el aprendizaje de otros contenidos geométricos, como las transformaciones geométricas y la comprensión de los cuerpos geométricos.
Para terminar, y teniendo en cuenta que las figuras prototípicas condicionan la comprensión de las figuras, se debería complementar su uso con una variedad de ejemplos de figuras como los usados en esta investigación, junto con materiales manipulativos, para que los niños puedan integrar lo conceptual (uso de los diferentes atributos y definiciones de las figuras) con lo perceptual, potenciando las verbalizaciones (Martin et al., 2007; Tsamir et al., 2008).











 nueva página del texto (beta)
nueva página del texto (beta)