1. INTRODUCCIÓN
Uno de los retos más importantes al que nos enfrentamos durante la educación científica y matemática es la resolución de problemas. Heyworth (1999), veinte años atrás, ya afirmaba que la enseñanza en las ramas de ciencia tiene general-mente como fin alcanzar dos objetivos: la adquisición de un cuerpo de conoci-miento organizado en un dominio particular y la habilidad para resolver problemas en ese dominio. El NCTM (National Council of Teachers of Mathematics) con “An Agenda for Action” en la década de los 80, la ATM (Association of Teachers of Mathematics) inglesa con el informe Cockcroft, los Estándares Curriculares del NCTM desde el año 1989 al 2000, son algunos de los ejemplos de la tradición y tendencia que la resolución de problemas matemáticos tiene como punto esencial en la educación obligatoria.
El debate sobre qué consideramos que es un problema en matemáticas y qué uso se le da a la resolución de problemas dentro del currículo educativo, ha sido uno de los puntos clave que guio el presente estudio. En la literatura no existe un consenso sobre qué entendemos por resolución de problemas. Grugnetti y Jaquet (2005) sugieren que esta falta de consenso se debe a las diferentes visiones existentes sobre la naturaleza de la actividad matemática. En la presente investigación seguiremos la nomenclatura que proponen Kantowski (1977) y Mayer (1985). De aquí en adelante, consideraremos el término problema como sinónimo de problema no rutinario. Dichos problemas requieren de creatividad e imaginación para proceder a su resolución puesto que, ante una situación inicial, el resolutor no conoce a priori un camino directo para conseguir su objetivo. Además, permiten poner el énfasis en el proceso de resolución, dada su riqueza, y no solo valorar el resultado final (Monje et al., 2012).
Dada la complejidad de la actividad de resolución de problemas, el dominio metacognitivo del resolutor es uno de los factores clave para su éxito. Diversos autores señalan que la metacognición es uno de los componentes básicos del aprendizaje autorregulado (Babbs y Moe, 1983; Novak y Gowin, 1988; Spring, 1985; Zimmerman, 1990; Zimmerman y Martínez-Pons, 1990) por eso, es de especial interés dentro de la investigación que nos ocupa.
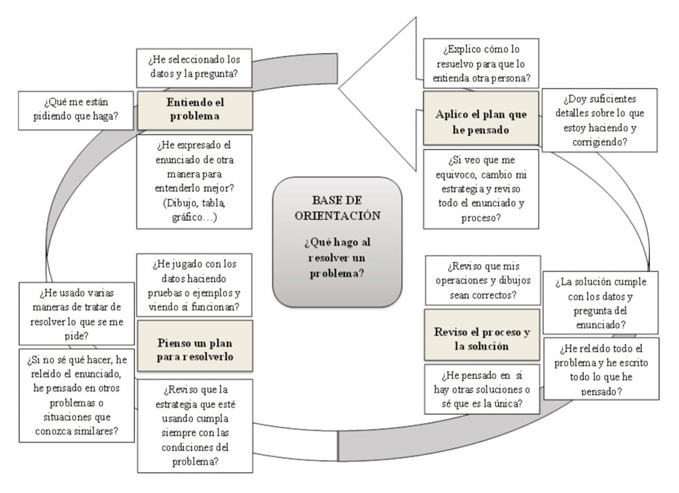
Existen diversos instrumentos de autorregulación matemática que contribuyen a estructurar los procesos metacognitivos del alumnado, uno de ellos es la base de orientación (Jorba y Sanmartí, 1996). Este instrumento fue diseñado inicialmente para guiar al alumnado durante el desarrollo y comprensión de procesos científicos y matemáticos de manera secuencial y lineal, es decir, paso a paso. La base de orientación conjuga conceptos y procedimientos algorítmicos concretos permitiendo al alumnado estructurar eficazmente su pensamiento. Las distintas bases de orientación desarrolladas y estudiadas por Jorba y Sanmartí (1996) nos muestran las potencialidades de autorregulación que presenta el instrumento a nivel matemático. Aunque la base de orientación no se diseñó inicialmente para ser usada durante la resolución de problemas, Villalonga y Deulofeu (2015) elaboraron y aplicaron una con alumnos de último curso de educación primaria y primer curso de educación secundaria durante un ciclo de resolución de problemas. En sus conclusiones señalan que el instrumento pue-de ser aplicado durante procesos no algorítmicos, como es la resolución de un problema matemático, puesto que se obtienen múltiples beneficios didácticos.
La principal diferencia respecto al planteamiento y diseño de Jorba y Sanmartí (1996) es que la base de orientación en resolución de problemas sintetiza y estructura distintas acciones y procedimientos que pueden ayudar al alumnado a resolver un problema. Por lo tanto, el propio alumno es quien elige cuáles de estas acciones y procedimientos le son útiles al resolver el problema que se le plantea. En cambio, las bases diseñadas para procesos algorítmicos de la ciencia y la matemática, sintetizan y conjugan teoría y práctica de tal modo que se deben seguir estrictamente para responder a la tarea planteada. Al finalizar su estudio, Villalonga y Deulofeu (2015) señalaron que, aunque la potencialidad del instrumento es evidente, el formato listado paso a paso dificulta su uso por parte del alumnado. Este hecho se produce dado que cuando resolvemos un problema, podemos usar multitud de caminos para hallar la solución y los procesos metacognitivos que entran en juego se configuran de manera distinta en cada resolutor. En la mayoría de los casos el proceso de resolución de un problema matemático no es secuencial o lineal, aunque la solución presentada al final del proceso sí lo sea.
Por lo tanto, la contribución principal de nuestro estudio es explorar el uso de una base de orientación como herramienta para promover los procesos metacognitivos en resolución de problemas de patrones. Para ello, caracterizamos los procesos metacognitivos del alumnado con la finalidad de observar cómo actúa la base de orientación en términos de metacognición y en qué momentos observamos que su linealidad presenta inconvenientes. Las características de estos momentos y su relación con los elementos metacognitivos son los que nos permitirán justificar la reconstrucción de la base de orientación.
2. MARCO TEÓRICO
2.1 Resolución de problemas y metacognición
Tal y como apunta Martínez (2008) la resolución de problemas matemáticos ha sido estudiada por una gran masa de expertos a lo largo y ancho de la historia. Lester, Garofalo y Kroll (1989) apreciaron cómo a medida que nos acercábamos a finales del siglo XX, los aspectos metacognitivos, sociales y afectivos empezaban a tomar una posición relevante en las investigaciones sobre resolución de problemas. A través de sus estudios, distinguieron cinco categorías interdependientes que intervienen en el resolutor de problemas: los conocimientos, el control, las creencias, los afectos y los factores contextuales. Posteriormente, Schoenfeld (1992) complementó y afinó las categorías antes descritas ya que consideraba que, las creencias y afectos debían considerarse como una única categoría en el resolutor por su cercanía y alta conexión. Así pues, éste último autor redefinió los cinco aspectos que intervienen en el resolutor: conocimiento de base, estrategias de resolución, gestión y control, creencias y afectos, y prácticas. La gestión y el control, entendidas como autorregulación y monitoreo del resolutor, pertenecen a una categoría más amplia a la que llamamos metacognición. La metacognición se refiere a la capacidad de reflexionar, comprender y controlar el propio aprendizaje (Ullauri y Ullauri, 2018). Flavell (1979) acuñó este término por primera vez y lo definió como:
El conocimiento sobre los propios procesos y productos cognitivos, así como el cono-cimiento sobre las propiedades de la información, datos relevantes para el aprendizaje o cualquier cosa relacionada con los procesos y productos cognitivos (citado en Campanario y Otero, 2000, p. 232).
Dentro del concepto de metacognición, Flavell (1979) diferenció dos categorías: el conocimiento de la cognición y la regulación de la cognición. Cuando hablamos de conocimiento sobre la cognición nos referimos al conocimiento que tiene una persona de sus capacidades cognitivas. En cambio, el estudio que nos ocupa se centra en la regulación de la cognición definida por Callahan (1987) y Clarke (1989) como aquellas decisiones que uno toma para:
Regular: Tomar consciencia de las decisiones necesarias para planificar y usar los procesos de resolución
Tomar consciencia: Monitorear dichas acciones atendiendo a su efectividad en términos de estrategias
Evaluar: Valorar la situación y evaluar la solución
Teniendo en cuenta que los procesos metacognitivos se dan de manera mental y subjetiva, el análisis de la metacognición se presenta como una tarea compleja que presenta limitaciones en distintas investigaciones (Ericsson y Simon, 1980). Encontramos en la literatura varios estudios que analizan los procesos metacognitivos de manera cuantitativa (Artzt y Armour-Thomas, 1992; Schraw y Sperling-Dennison, 1994; Sperling et al., 2002). Gran parte de estos estudios usan cuestionarios como el MAI (Metacognitive Awareness Inventory) para identificar las habilidades metacognitivas del alumnado. Aunque dichos estudios permiten muestreos amplios, no atienden a procesos metacognitivos concretos de los estudiantes ni a contextos didácticos específicos. En cuanto a los estudios cualitativos, los protocolos en voz alta son los más usados por los investigadores (Wilson y Clarke, 2004). En estos casos se pide al alumno que verbalice el pro-ceso de resolución de un modo concurrente o retrospectivo, es decir, mientras realiza el problema o una vez que lo ha finalizado. Aunque este método permite un análisis exhaustivo de los procesos metacognitivos, puede propiciar que el alumnado de baja edad se bloquee durante la explicación o incluso invente pasos durante su retrospectiva (Ericsson y Simon, 1980). Dadas las limitaciones aportadas y atendiendo a la etapa en la que nos encontramos, cursos superiores de educación primaria, las producciones escritas del alumnado pueden ser una herramienta eficaz para analizar y caracterizar los procesos metacognitivos (Martínez et al., 2020).
Dentro del campo de la didáctica matemática, existen distintos instrumentos de autorregulación metacognitiva. En primer lugar, encontramos los diarios de clase en los que el alumnado anota individualmente aspectos referentes al proceso de enseñanza y aprendizaje realizado (Rodríguez y Bisbal, 2014). Los diarios de clase son muy útiles para explicitar y reflexionar sobre las tareas matemáticas pero al ser elaborados individualmente, no permiten que el alum-nado comparta con fluidez los procesos metacognitivos llevados a cabo. En segundo lugar, encontramos los mapas conceptuales que permiten estructurar conceptos y procedimientos complejos estableciendo una estructura jerárquica en una cierta área de conocimiento (Morales, 1998). En cuanto a la resolución de problemas, los mapas conceptuales pueden ser útiles en términos de relación entre conceptos y procedimientos matemáticos, pero no contemplan explícita-mente la inclusión de procesos metacognitivos. En tercer lugar, encontramos la V de Gowin (Escudero y Moreira, 1999) dividida en tres dominios: el dominio conceptual, el dominio metodológico y el objetivo o acontecimiento. En este caso, el instrumento en sí contempla procesos metacognitivos en el dominio metodológico, pero no contiene una estructura interna que atienda a las fases de resolución de un problema (Polya, 1945). Por último, encontramos las bases de orientación (Jorba y Sanmartí, 1996) que contemplan tanto la inclusión de procesos metacognitivos como de destrezas matemáticas (Puig, 1996) y que además, pueden ser estructuradas atendiendo a las fases de resolución de un problema. Dada la investigación que nos ocupa y las características expuestas, la base de orientación es el instrumento propicio para fomentar la explicitación de los procesos metacognitivos del alumnado.
2.2 La base de orientación
Aplicación en constructos teóricos y prácticos lineales
Jorba y Sanmartí (1996), crearon, desarrollaron y analizaron la base de orientación como instrumento estructurador y orientador de los modelos teóricos de la ciencia, aplicados a la práctica cercana del alumnado. García y Sanmartí (1998) observaron que, aunque los alumnos sepan definir diferentes conceptos como “hongo, heterótrofo, saprófito y ser vivo, ello no presupone que al mostrarles un trozo de pan enmohecido puedan explicar este fenómeno” (p. 9). La base de orientación es un instrumento pensado específicamente en el área de ciencias naturales y matemáticas:
Un instrumento ideado para promover que el alumnado desarrolle su capacidad de anticipar y planificar las operaciones necesarias para realizar una acción. A través de ella se pretende que explicite los procesos que se deben realizar o que se han realizado al ejecutar una tarea, o las características que permiten definir un modelo o un concepto. […] La base de orientación ayuda a desarrollar la habilidad de seleccionar las características relevantes y a anticipar un plan de acción (García y San-martí, 1998, p. 10-11).
Puesto que no existe en la literatura una definición que nos permita diferenciar la base de orientación de otro instrumento de autorregulación la definiremos, para el propósito de esta investigación, como un instrumento secuencial paso a paso en el cual se sintetizan de manera subjetiva o personal las acciones a realizar durante un procedimiento científico o para explicar un constructo teórico. A medida que se producen nuevos aprendizajes, la base de orientación se amplía o reestructura adaptándose al proceso de autorregulación de quien la elabora. En el presente estudio el uso de la base de orientación se concibe como un fin en sí mismo, es decir, como un medio para potenciar la explicitación y verbalización de los procesos metacognitivos en resolución de problemas, quedando el aprendizaje de conceptos y métodos concretos en un segundo plano. Por lo tanto, el interés principal del instrumento es la autorregulación del alumnado durante la resolución de un problema y no tanto el aprendizaje de un contenido o proceso matemático concreto tal y como plantean en su diseño Jorba y Sanmartí (1996).
Podríamos asimilar la base de orientación a una rúbrica holística en la cual, la descripción del máximo nivel de desempeño de cada criterio de evaluación se correspondería con cada una de las acciones que aparecen en la base de orientación. Cano (2015) define una rúbrica holística como una matriz de valoración que incorpora en un eje los criterios de evaluación y en otro eje una escala de valor donde se tipifica qué ejecución debería hacer el resolutor para considerarse dentro del nivel correspondiente a cada criterio. Según Alsina (2018) las rúbricas enuncian “criterios de logro y descriptivos […] permiten ser cambiadas y ajustadas durante la práctica para así encontrar el valor justo que se pretende que los alumnos alcancen” (p. 13). Este último apunte es aplicable del mismo modo a la definición de base de orientación.
Las premisas que nos define Sanmartí (2010) ante la gestión de la base de orientación, son diversas. En primer lugar, hace especial énfasis en el pro-ceso de elaboración de la base. Aunque por motivos temporales, por falta de conocimiento del instrumento o por tratarse de constructos conceptuales, la base de orientación puede ser elaborada por el profesor, lo más idóneo es que sea construida por el alumnado (García y Sanmartí, 1998). Atendiendo al objetivo del estudio que nos ocupa, si pretendemos que la base de orientación propicie la aparición y explicitación de procesos metacognitivos propios, tiene sentido que sea el propio alumnado quien la elabore y modifique. En este caso, el proceso de creación será orientado y dirigido por el docente a través de preguntas clave (tabla 1) sin olvidar que deben ser los mismos alumnos quienes le den forma y sentido.
Tabla 1 Preguntas clave para la creación de la base de orientación (izquierda) y caracterización / finalidad de dichas preguntas (derecha)
| Elementos estructurales de la acción | |
|---|---|
| ¿A qué categoría pertenece la situación planteada? | Identificación del problema |
| ¿Por qué se debe realizar esta tarea? | Motivo de la tarea |
| ¿Qué se quiere conseguir con la realización de la acción que interviene como solución de la tarea? | Objetivo de la acción |
| ¿Qué operaciones es necesario realizar para ejecutar la acción y por qué? | Operaciones de la acción |
| ¿Qué conocimientos son necesarios para efectuar de manera consciente estas operaciones? | Contenidos de la base |
| ¿En qué condiciones tenemos que realizar la tarea planteada? | Condiciones de realización |
| Anticipación de la acción | |
| ¿Qué estrategia o estrategias se pueden adoptar para resolver la situación planteada? | Estrategias y orden de ejecución |
| ¿Cuál es el resultado esperado de las operaciones proyectadas? | Posibles resoluciones |
| Planificación de la acción | |
| ¿Cuál de las estrategias parece la más adecuada? | Elección de la estrategia |
| ¿Cuál es el plan de ejecución que seguiremos? | Plan de trabajo |
En segundo lugar, al tratarse de una construcción totalmente personal de la tarea a trabajar, puede haber tantas bases de orientación como alumnos se encuentren en el aula. Cada alumno da su propio formato a la estructuración y resolución de una misma tarea. En este punto, entra en juego la tercera premisa. Las bases de orientación deben ser evaluadas y reguladas a partir de autoevaluación o coevaluación. Aunque sea un instrumento basado en la propia percepción del problema o en la aplicación de un constructo teórico en el caso de procesos algorítmicos, debe tener criterio científico. Las bases y los ítems que en ella se encuentran no son aleatorios; hay unas premisas u otras a seguir dependiendo de la aplicación final de dicha base.
Aunque la base de orientación ayuda al alumno a planificar el proceso de resolución y lo dota de acciones y procedimientos que le son de ayuda al enfrentarse a una tarea, es el hecho de introducir instrumentos autorregulativos como la autoevaluación y coevaluación lo que promueve que el alumno desarrolle procesos metacognitivos complejos. Por lo tanto, la finalidad de la evaluación no es realizar preguntas directas y estancas sobre el proceso de resolución sino realizar preguntas que permitan al alumno reflexionar sobre su propio pensamiento y sobre su propia práctica. Este hecho es el que permitirá emerger procesos metacognitivos complejos que se incorporarán en la base de orientación a medida que el alumnado la usa.
Por último, debemos tener en cuenta que la base de orientación no se crea y permanece inmutable, sino que se transforma a partir del aprendizaje paula-tino del alumnado.
Contribuyen a la elaboración progresiva de las bases de orientación todas aquellas situaciones didácticas que promuevan la reflexión de los estudiantes sobre aquello que están aprendiendo, cómo lo están aprendiendo y qué dificultades encuentran, así como aquellas situaciones que propicien el contraste de puntos de vista y opiniones (García y Sanmartí, 1998, p. 14).
Jorba y Sanmartí (1996) nos plantean y ejemplifican diferentes bases de orientación creadas con el alumnado, por ejemplo: Cómo se calcula la densidad, cómo se caracteriza una especie animal, qué pasaría si desapareciera una especie de una red trófica, cómo se mide de manera indirecta, cómo se construye y lee un gráfico, y cómo se representa a escala.
Aplicación durante la resolución de problemas
Una vez examinada la funcionalidad de la base de orientación para la construcción, apropiación y aplicación de constructos teóricos en ciencias y matemáticas, Villalonga y Deulofeu (2017), la aplicaron al ámbito matemático durante la resolución de problemas. Teniendo en cuenta las limitaciones temporales de su estudio, la base de orientación propuesta por los autores estaba previamente elaborada (tabla 2) y a partir de su uso, los alumnos podían añadir, quitar o modificar aquellas concreciones que considerasen oportunas. Dicha base, se basa en las fases de resolución de un problema aportadas por De Corte et al., (2000b), De Corte y Verschaffel (2003) y las propuestas de Mason et al., (1982).
Tabla 2 Base de orientación creada por Villalonga y Deulofeu (2017, p.266) aplicada a la resolución de problemas matemáticos
Una de las conclusiones a las que llegaron los autores, fue la dificultad del alumnado de comprender que la linealidad de la base de orientación actúa meramente como guion y no como una pauta que se sigue de manera estricta: “se confirma así que la resolución un problema es una dinámica compleja, en ningún caso lineal, que requiere de tiempo, reflexión y dedicación” (Villalonga y Deulofeu, 2017, p. 279). Se justificó su formato listado de la siguiente manera:
La linealidad establecida, cuyo orden se sustenta por las fuentes usadas y que describen los pasos de un resolutor experto, se convino para posibilitar un orden de aplicación, evitar dispersiones, y al mismo tiempo establecer de manera clara y precisa la relación entre dominios, dimensiones, y ambos (Villalonga y Deulofeu, 2017, p. 265).
Como hemos podido observar en la ejemplificación anterior referente a la base de orientación en resolución de problemas, este instrumento une por un lado, el ciclo de resolución de un problema y por otro, la regulación de la cognición atendiendo a ítems de consciencia y monitoreo como “si no lo consigo, detecto dónde me bloqueo o me equivoco y aplico una nueva estrategia” (tabla 2).
En el presente estudio se replanteará la creación y uso de la base de orientación como una unión de los dos planteamientos presentados a nivel estructural por Villalonga y Deulofeu (2017) y a nivel metacognitivo por Clarke (1989).
3. OBJETIVO Y DISEÑO DEL ESTUDIO
A la luz de las consideraciones teóricas expuestas y los antecedentes presentados, la finalidad del presente estudio es determinar cómo actúa la base de orientación como instrumento de verbalización escrita de los procesos metacognitivos durante la resolución de problemas. Así pues, nuestro objetivo es caracterizar los procesos metacognitivos escritos derivados de la creación y aplicación de una base de orientación. Identificar estos procesos nos debería permitir reelaborar el concepto de base de orientación para adaptarlo a la naturaleza de la resolución de problemas.
Los datos del estudio se recogieron en tres centros del área metropolitana de Barcelona. Participaron un total de 75 alumnos de sexto grado de educación primaria con edades comprendidas entre los 11 y 12 años. Cabe mencionar que en los tres centros se trabaja con problemas una hora a la semana en formato taller. Los alumnos se agrupan de manera individual o por parejas para proceder a la resolución de los problemas. Habitualmente, los docentes de aula presentan los problemas al alumnado, se procede a resolverlos y finalmente se realiza una puesta en común. Ninguno de los centros conocía ni trabajaba con la base de orientación.
En primer lugar, se seleccionaron dos problemas (figura 1) que originaban esencialmente la numeración y los patrones matemáticos. La selección de dichos problemas se realizó atendiendo a la flexibilidad que caracteriza los problemas de patrones, entendida como la variabilidad de estrategias de distinta complejidad que se pueden aplicar (Callejo y Zapatera, 2014). Puesto que se trató de un estudio no interviniente, se realizaron tres reuniones con los respectivos docentes con la finalidad de presentar la estructura y utilidad de la base de orientación, así como los dos problemas a trabajar.

Figura 1 Adaptación de dos problemas de lógica y patrones matemáticos obtenidos de FEEMCAT, SCM, Generalitat de Catalunya (2000-2018). Problemes a l’esprint. http://www.cangur.org/esprint/ [enero 2020].
En la primera sesión, los docentes plantearon al alumnado las preguntas clave para proceder a la elaboración de la base de orientación que hemos concretado en la tabla 1. Las ideas del alumnado fueron anotadas en la pizarra y a partir de una conversación en gran grupo, se conformó un formato lineal de base de orientación con dos columnas: en la columna de la izquierda se anotaron los procesos metacognitivos y destrezas matemáticas para resolver estos problemas (ítems que conforman la base) y a la derecha de cada uno, se incluyó una columna en la que el alumnado anotaría con una cruz qué ítems usaban o no usaban al aplicar la base. Una vez elaborada la base de orientación, el alumnado resolvió el primer problema individualmente. Se realizó una puesta en común sobre las posibles estrategias y soluciones encontradas.
En una segunda sesión, se pidió al alumnado si deseaba modificar la base de orientación atendiendo a las observaciones que habían realizado durante la resolución del primer problema y a los procesos y destrezas usadas y no usadas. Posterior-mente, se procedió a resolver el segundo de los problemas con la base de orientación modificada y se pusieron en común las distintas resoluciones y estrategias.
4. MÉTODOS DE ANÁLISIS
Los datos obtenidos se conforman a partir de la base de orientación creada, su modificación previa al segundo problema y las producciones escritas del alumnado.
El primer análisis de las producciones, por parte de los tres autores del estudio, se realizó elaborando una rúbrica holística de cuatro niveles (novel, intermedio, avanzado y experto) para cada ítem de la base de orientación creada. La diferenciación en cuatro niveles atiende a la carencia de posicionamiento central en caso de duda (Raposo y Martínez, 2011). La concreción de cada nivel elaborado corresponde a dos necesidades de análisis: observar el uso de un determinado ítem y la verbalización escrita y explícita del mismo. Así pues, el nivel novel hace referencia a un ítem no usado, el nivel intermedio se refiere a un ítem usado, pero no verbalizado por escrito, el nivel intermedio a un ítem usado y verbalizado parcialmente y el nivel experto a un ítem usado y verbalizado exhaustivamente. La finalidad de dicha rúbrica no era obtener una visión global del nivel de desempeño de cada alumno, sino obtener una visión concreta sobre cada ítem con la finalidad de realizar la segunda fase de análisis. Por lo tanto, se procedió a evaluar individualmente las producciones de los dos problemas planteados, atendiendo al uso y verbalización escrita de cada ítem. Al realizar este primer análisis, observamos que en el segundo problema el alumnado mostraba un mayor conocimiento del uso de la base de orientación puesto que era la segunda vez que la usaban. Se decidió considerar para la segunda fase de análisis, aquellas producciones referentes al segundo problema que mostraban niveles avanzados y/o expertos para cada uno de los ítems de la base.
En la segunda fase de análisis se procedió a caracterizar los procesos meta-cognitivos de las producciones seleccionadas en la primera fase. Realizamos un análisis inductivo de las producciones del alumnado tal y como lo realizan Kuzle (2013) y Magiera y Zawojewski (2011). En primer lugar, elaboramos una categorización externa identificando los procesos metacognitivos que aparecen en
las producciones atendiendo a la definición de consciencia, evaluación y regulación de Clarke (1989). Una vez identificados estos procesos, se realizó a una categorización interna de las producciones del alumnado basada en el contexto del problema que habían resuelto. Por lo tanto, se seleccionaron todos los procesos referentes a evaluación, consciencia y regulación respectivamente y, se establecieron similitudes y diferencias entre ellos. Este análisis nos permitió establecer nueve categorías derivadas de los distintos procesos metacognitivos. La tabla 3 muestra las nueve categorías elaboradas, así como la concreción observable en las producciones, es decir, qué acciones lleva a cabo el alumna-do durante la resolución que nos refieren a cada una de las categorías. Cabe mencionar que la numeración ascendente de la tabla 3 no corresponde a un criterio de importancia u orden.
Tabla 3 Concreción de los procesos metacognitivos, categorías y concreción observable en la producción (elaboración propia)
| Proceso metacognitivo | Categoría | Concreción |
|---|---|---|
| Consciencia | 1. Explicitación del proceso de solución. | Es consciente de los pasos que realiza de manera lineal. |
| 2. Consciencia del patrón. | Es consciente de que hay un patrón tras el dibujo y lo verbaliza. | |
| 3. Selección de la estrategia. | Es consciente de que hay estrategias más rápidas y eficaces que otras. | |
| Evaluación | 4. Revisión de la solución. | Comprueba su resultado final en coherencia con el enunciado. |
| 5. Revisión del proceso. | Comprueba las operaciones aritméticas y el patrón del dibujo realizado. | |
| 6. Revisión doble. | Busca otras razones o argumentos para comprobar su resultado final. | |
| Regulación | 7. Planificación y ejecución. | Planifica, reconoce la estrategia a usar y la verbaliza. |
| 8. Relectura y verificación. | Relee el enunciado en varios momentos para comprobar su proceso. | |
| 9. Adaptabilidad y regulación. | Sufre un atasco o bloqueo, lo evalúa y lo supera adaptando su estrategia. |
5. RESULTADOS: VERBALIZACIÓN DE PROCESOS METACOGNITIVOS4
Siguiendo el objetivo de nuestro estudio, mostraremos la caracterización de los procesos metacognitivos llevados a cabo por el alumnado.
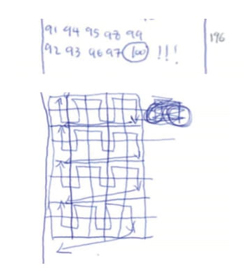
En la primera categoría establecida: explicitación del proceso de solución, observamos producciones en las que se expresa una resolución paso a paso tal y como se presentan en la base de orientación. En primer lugar, notamos que se redactan los pasos realizados expresándolos en forma de párrafo escrito (tabla 4 - figura 2). En segundo lugar, encontramos producciones en las que incluso se numeran los pasos en formato listado obteniendo así una resolución del problema pautada como si de una receta se tratara (tabla 4 - figura 3). Obser-vamos en ambos casos que el alumnado es consciente grosso modo de los pasos realizados desde la lectura del problema hasta su solución final o revisión. Además, ambos alumnos verbalizan procesos metacognitivos complejos (Montague, 2008) que van más allá de la mera descripción del proceso como puede ser “he buscado la lógica” (figura 2) o “he llenado la casilla como la de arriba, pero con otros datos” (figura 3).
Tabla 4 Explicitación del proceso de solución: transcripción al castellano (izquierda), producción original (derecha)
En la segunda categoría establecida: consciencia del patrón, observamos producciones en las que se expresa por escrito el patrón oculto tras la tabla con expresiones y recursos distintos. En primer lugar, observamos el uso del dibujo como destreza matemática para verbalizar la consciencia del patrón. En este caso, el alumno añade como finalizaría el patrón de la tabla sin llegar a completarla por completo (tabla 5 - figura 4). En segundo lugar, observamos una estrategia sumamente distinta; en vez de realizar toda la tabla por completo, se reconoce el patrón al inicio y sólo se completa la tabla a partir del número 91 (tabla 5 - figura 5). Por último, observamos otra producción en la que el alumno nos explicita de manera gráfica qué patrón sigue la tabla, encontrando así, las dos últimas hileras que le sirven para resolver el problema (tabla 5 - figura 6). En los tres casos expuestos, observamos que el alumno es consciente de que hay un patrón tras el dibujo y que la finalización completa de la tabla no es una condición estricta para resolver el problema. Este hecho nos remite a la tercera categoría metacognitiva establecida, en la cual el alumno selecciona una estrategia siendo consciente en los tres casos de que es más rápida y eficaz que otras; por ejemplo, el ensayo-error durante la probatura de números o la finalización completa de la figura (Maclellan, 2014).
Tabla 5 Consciencia del patrón y selección de la estrategia: transcripción/interpretación de la producción al castellano (izquierda), producción original (derecha)
| Transcripción literal al castellano / Interpretación | Fragmento original en catalán |
| Interpretación: El alumno es consciente del patrón que sigue la tabla y añade al dibujo inicial las décimas de la serie compuesta por el número 90 añadiendo el número 100 dónde se encontraba inicialmente el número 10 para así completar las condiciones del enunciado. |
Figura 4. Producción original (PPEP6_A19) consciencia del patrón y selección de estrategia. |
| Suman 294 lo he sabido porque he mirado el patrón y lo he aplicado desde el 91 hasta el 100 y sólo ha hecho falta sumar 99+98+97. He mirado el dibujo y he identificado cómo se posicionaban los números, he hecho lo mismo con los números del 91 hasta el 100. He mirado cuales tocaban y he visto el 99, 98, 97 los he sumado y me ha dado el resultado. |
Figura 5. Producción original (PPSFP6_A17) consciencia del patrón y selección de estrategia. |
| Interpretación: El alumno nos muestra el patrón que sigue la tabla a partir de las flechas y encuentra la lógica que sigue la numeración poniendo por escrito la serie del 91 al 100. |
Figura 6. Producción original (PPSFP6_A29) consciencia del patrón y selección de estrategia. |
En cuanto a la cuarta y quinta categorías establecidas: revisión de la solución y revisión del proceso, encontramos que en gran parte de las producciones analizadas los alumnos verbalizan explícitamente que han revisado la solución final obtenida rehaciendo la suma final o bien, a través del cálculo mental. Este proceso de revisión se realiza de dos modos distintos. Por un lado, encontramos alumnos que vuelven a leer el enunciado para confirmar su procedimiento y respuesta (tabla 6 - figura 7) y por otro, encontramos alumnos que al releer el enunciado y ante la duda de sumar (o no) el número 100, ofrecen dos soluciones posibles (tabla 6 - figura 8). Dicho proceso metacognitivo explícito muestra que éste último el alumno, ante la imposibilidad de comprender completamente el enunciado, opta por ofrecer dos soluciones viables dependiendo de la comprensión y enfoque que le da a la pregunta del problema (Van der Stel et al., 2010).
Tabla 6 Revisión de la solución y revisión del proceso: transcripción de la producción al castellano (izquierda), producción original (derecha)
| Transcripción literal al castellano | Fragmento original en catalán |
|
|
Figura 7. Producción original (PPSFP6_A18) revisión de la solución. |
|
|
Figura 8. Producción original (PPPDP6_A12) revisión de la solución y del proceso. |
En cuanto a la sexta categoría: revisión doble, observamos producciones en las cuales el alumnado coteja la solución obtenida con una nueva comprobación a través de otro método o estrategia (tabla 7 - figura 9). Este hecho posibilita la seguridad, por parte del alumno, de que la solución obtenida es correcta y además, verbaliza su comprobación. Tal y como apunta Sanmartí (2010) se trata de una autoevaluación del proceso que se realiza en el momento de finalizar la tarea, para corroborar la veracidad y satisfacción del procedimiento realizado, así como de su resultado.
Tabla 7 Revisión doble: transcripción de la producción al castellano (izquierda), producción original (derecha)
| Interpretación en castellano | Fragmento original |
| Interpretación: El alumno toma consciencia del patrón al inicio y en vez de completar la tabla del 1 al 100, decide dibujar sólo del número 72 al 100 hallando así la solución al problema. Posteriormente, escribe el número 9 delante de los números 7 y 9 del dibujo, respectivamente, confirmando así que el dibujo realizado por ella misma casa con la figura inicial propuesta. |
Figura 9. Producción original (PPEP6_A21) consciencia del patrón. |
En cuanto a la séptima categoría: planificación y ejecución, observamos producciones en las cuales el alumnado planifica meticulosamente la estrategia a usar observando detenidamente la tabla y analizando por columnas la similitud entre el orden de los números antes de proceder a la ejecución del plan (tabla 8 - figura 10). Observamos en este caso que el alumno numera las columnas y establece una leyenda para encontrar qué patrón sigue la tabla inicial. Una vez encontrado el patrón, completa la tabla para verificar que su hipótesis inicial era cierta y así poder finalizar la resolución del problema. Atendiendo a Polya (1945) la planificación del plan de acción es una tarea tan o más importante que la ejecución del propio plan. Schoenfeld (1992) destaca esta habilidad como una propia del resolutor experto, en el cual, el tiempo de planificación de la estrategia a seguir así como la relectura de las condiciones originales, ocupa una posición central en la resolución de un problema.
Tabla 8 Planificación y ejecución: transcripción de la producción al castellano (izquierda), producción original (derecha)
En cuanto a la octava categoría: relectura y verificación, hemos observado tal y como muestra la tabla 4, que en ciertos momentos el alumnado dentro de la linealidad de sus explicaciones verbaliza explícitamente releer el enunciado para corroborar que su proceso y su estrategia siguen cumpliendo con los requisitos, datos y pregunta del problema. En conjunción con esta categoría, encontramos una alumna que, al releer y verificar el enunciado, se da cuenta de que ha cometido un error y pone en marcha la novena categoría caracterizada como adaptabilidad y regulación para poder superar el atasco que se produce (Villa-longa y Deulofeu, 2017) y cumplir con las condiciones que explicita el enuncia-do (tabla 9 - figura 11).
Tabla 9 Relectura, verificación, adaptabilidad y regulación: transcripción de la producción al castellano (izquierda), producción original (derecha)
6. DISCUSIÓN
Al inicio del estudio, nos planteamos como objetivo caracterizar los procesos metacognitivos escritos derivados de la creación y aplicación de una base de orientación. En la sección anterior, caracterizamos los procesos observados referentes a la consciencia, evaluación y regulación (Clarke, 1989) concretados en la tabla 3. En este apartado nos parece relevante discutir la importancia de su uso y verbalización.
En primer lugar, hemos observado tal y como apuntan Villalonga y Deulofeu (2017) que la explicitación detallada de la resolución en estas edades produce una mayor consciencia del proceso realizado y por ende, promueve que el alum-nado se autorregule de manera más efectiva. Este hecho posibilita que el resolutor pueda evitar un posible atasco o bloqueo a partir de la relectura y reflexión de su propio proceso. Así pues, observamos una estrecha relación entre las categorías explicitación del proceso de solución (1) y adaptabilidad y regulación (9).
En segundo lugar, coincidimos con Lester (1994) al observar que la metacognición efectiva durante la resolución de problemas requiere saber no solo qué y cuándo monitorear, sino también cómo monitorear. Las categorías referentes a planificación y ejecución (7) así como relectura y verificación (8) nos muestran la importancia de explicitar por escrito la planificación del problema para poder verificar en varios momentos que dicha planificación se adapta a las condiciones dadas al inicio. Este hecho nos muestra una alta capacidad de autorregulación al resolver un problema, y dada la edad de los resolutores, es un indicador clave en su desarrollo hacia convertirse en resolutores expertos (Schoenfeld, 1989).
En tercer lugar, observamos la importancia que desempeña la fase de evaluación -en este caso, autoevaluación- en el proceso de resolución. Nos parece oportuno destacar que las categorías de revisión de la solución (4) y revisión del proceso (5) deberían ser inseparables al resolver un problema, aunque encontramos casos en los que o bien no se dan, o bien se da una sin la otra (tabla 6). El proceso de autoevaluación es una de las claves del éxito escolar (Sanmartí, 2010) así como del éxito en resolución de problemas. Observamos, además, que los casos en los que se realiza una revisión doble (6) -usando otro método para verificar la solución-, son los casos en los que no solo se producen menos errores en la resolución y solución final sino que además, se evita la selección de estrategias de resolución erróneas (3).
Por último, encontramos una estrecha relación entre la consciencia del patrón (2), es decir, el modo en el que el alumnado percibe el patrón de la tabla, y la selección de la estrategia de resolución (3). En los casos en los que el alumnado percibe solo el patrón pictórico -colocación específica de los números en la tabla a modo de cenefa- la estrategia seleccionada tiende a ser finalizar la tabla hasta llegar al número 100. En los casos en los que el alumnado percibe el patrón aritmético -la relación entre la distribución de los números por columnas- la estrategia seleccionada tiende a ser relacionar aritméticamente los números entorno al 100 sin llegar a finalizar la tabla. Así pues, observamos que esta última percepción aritmética del patrón conlleva a la selección de una estrategia de resolución más eficaz a nivel lógico-matemático y temporal.
7. CONCLUSIONES
Corroboramos que la creación de la base de orientación por parte del alumnado ha producido una mayor apropiación de las fases de resolución de un problema matemático, así como de los procesos metacognitivos que se desarrollan durante la resolución (Jorba y Sanmartí, 1996). Al usar la base de orientación, las producciones son más estructuradas y el alumnado hace un mayor esfuerzo por redactar detalladamente el proceso seguido. Este hecho produce que no solo se describa o explique el proceso matemático seguido sino que se llegue a justificar con procesos metacognitivos el porqué de determinadas elecciones (Godino y Llinares, 2000).
La caracterización de los procesos metacognitivos nos ha mostrado que la consciencia, evaluación y regulación son procesos que se producen de manera no lineal. Cuando nos referimos al término no lineal, hacemos referencia a que ante un mismo problema el alumnado conjuga los procesos metacognitivos de distinto modo para llegar a la solución. Por lo tanto, aunque la resolución escrita de un problema se presente de forma lineal, ya que cuenta con unos pasos de inicio a fin para hallar la solución, los procesos metacognitivos del alumnado para resolver el problema no son lineales y, por lo tanto, no existen dos resoluciones que cuenten con procesos mentales idénticos (Clarke, 1989). Tal y como hemos observado en el apartado de resultados, en diversas ocasiones el alumnado acata el hecho de “seguir la base de orientación” como una lista secuencial y cerrada e incluso resuelve el problema en formato listado numerando los pasos a seguir. Este hecho produce que en ocasiones, cuando se desarrollan procesos como releer, cambiar de estrategia o revisar continuamente, no se pongan por escrito de manera natural (Villa-longa y Deulofeu, 2015). Coincidiendo con Swanson (1990) y Mayer (1985) el proceso de resolución de un problema no es lineal, sobre todo en resolutores expertos. Así pues, llegados a este punto, consideramos oportuno aportar un nuevo formato de base de orientación (figura 12) para que ésta se adapte al ciclo de resolución no lineal y además cuente con los procesos metacognitivos caracterizados en este estudio. Denominamos a este nuevo instrumento Base de Orientación No Lineal.
Consideramos que la Base de Orientación No Lineal se adapta tanto a la realidad del proceso de resolución de un problema como a las aportaciones presentadas en esta investigación. Abrimos así una nueva línea de estudio en la que sería interesante observar si este nuevo formato se ajusta de manera más precisa al proceso de resolución.
A modo de cierre, señalamos la dificultad de examinar los procesos metacognitivos en resolutores de baja edad (Panaoura et al., 2003). Compartimos con los autores que realizan investigaciones en metacognición, la idea de que en la educación elemental o primaria examinar la metacognición de manera oral puede ser una ardua tarea, puesto que las respuestas del alumnado pueden reflejar lo que dicen (o no) al investigador y no lo que realmente piensan o hacen. Así pues, el formato escrito promovido por el uso de la base de orientación (Jorba y Sanmartí, 1996) permite al resolutor sentirse menos coaccionado por el investigador al resolver el problema por escrito e individualmente, por lo que consideramos que ayuda al estudio en el campo de la metacognición.











 nueva página del texto (beta)
nueva página del texto (beta)