Introducción
La convergencia económica es una cuestión teórica y políticamente importante para académicos, economistas, tomadores de decisiones y planificadores regionales; ésta se refiere al proceso en el que las regiones o países pobres (i.e. con menores niveles de ingreso per cápita) crecen económicamente más rápido que las regiones o países ricos. Empíricamente la hipótesis de convergencia se verifica a través del modelo de crecimiento neoclásico propuesto por Barro y Sala-i-Martin (1995), el cual impone una homogeneidad al proceso de convergencia hacia un único nivel de estado estacionario (i.e. tasa de crecimiento de largo plazo), proceso en el cual todas las economías crecen a una misma velocidad. No obstante, la literatura sugiere indagar sobre la existencia de diferentes estados estacionarios (Mankiw, Romer y Weil, 1992; Quah, 1996; Bernard y Durlauf, 1995; Temple, 1999) y el efecto del espacio en las dinámicas de crecimiento (Anselin, 1988; Abreu, de Groot y Florax, 2005; Rey y Janikas, 2005; Ertur, Le Gallo y LeSage, 2007; Ertur y Le Gallo, 2009; Mur, López y Angulo, 2010).
Lo anterior deriva en la inclusión, al análisis de convergencia, de la dependencia y la heterogeneidad espacial. La dependencia espacial se observa cuando la tasa de crecimiento en una región depende de los valores de las observaciones en regiones vecinas; mientras que la heterogeneidad espacial se observa cuando los parámetros estimados en los modelos varían entre regiones en función de su localización (Abreu et al., 2005). A pesar de que ambos efectos espaciales están intrínsecamente relacionados y pueden presentarse simultáneamente en datos de naturaleza espacial, la heterogeneidad ha sido menos analizada en comparación con la dependencia espacial. Por ello, la teoría moderna del crecimiento hace hincapié en que, para captar la heterogeneidad espacial, las diferentes economías deben ser descritas por una función de producción en particular (Ertur y Le Gallo, 2009).
En México, varios estudios han examinado el proceso de convergencia (e.g. Esquivel, 1999; Fuentes y Mendoza, 2003; Díaz, Sánchez y Mendoza, 2009; Ruíz, 2010, entre otros), los cuales dejan entrever que la dinámica de crecimiento económico es heterogénea. Otros estudios han hecho hincapié en el proceso de convergencia frente a la apertura comercial (Ito, 2010; Cabral y Varella, 2012; Ruíz, 2015) y la heterogeneidad resultante (Bayles, Garduño-Rivera y Piras, 2012; Díaz-Dapena, Fernández-Vázquez, Garduño-Rivera y Rubiera-Morollon, 2017; 2019), así como en las disparidades económicas regionales (Sastré-Gutiérrez y Rey, 2008; Rey y Sastré-Gutiérrez, 2010). Sin embargo, sólo algunos estudios han puesto a prueba la hipótesis de convergencia, lidiando con la no-estacionariedad del proceso, a través de series de tiempo (Cermeño, 2001; Carrion-i-Silvestre y German-Soto, 2008; Ayala, Chapa y Murguía, 2011). También, se han realizado estudios transversales para capturar la heterogeneidad espacial, a través de: 1) clubes de convergencia (Rodríguez, López y Mendoza, 2016; 2)) modelos espaciales (Valdivia, 2008, 2012; Asuad y Quintana, 2010; Rodríguez-Gámez y Cabrera-Pereyra, 2017; 2019); y 3) estimaciones locales (Calderón y Tykhonenko, 2007; Brida, Pereyra, Puchet-Anyul y Risso, 2013).
Sin embargo, el asumir una misma tasa de convergencia en todas las regiones no es realista y debe admitirse que la convergencia es un proceso no-estacionario, lo que implica la existencia de convergencia de algunas regiones y la divergencia en otras, atendiendo a un proceso de crecimiento no equilibrado (según la teoría de causación circular) o de múltiples equilibrios (de acuerdo con la teoría moderna del crecimiento). En este sentido, la heterogeneidad espacial, entendida como no-estacionariedad espacial del proceso de convergencia implica que, un modelo de regresión donde se estima un solo parámetro “global” (i.e. todas las observaciones se ajustan a un solo parámetro, por ejemplo, beta (β) o tasa de convergencia), no permite capturar las relaciones “locales” entre observaciones (Brunsdon, Fotheringham y Charlton, 1996; Fotheringham, Charlton y Brunsdon, 1997).
Por consiguiente, para capturar la heterogeneidad y los patrones locales y/o regionales que puedan perfilarse, la tasa de convergencia y su velocidad deben variar a través del espacio. Metodológicamente, esto es posible especificando regímenes espaciales. Sin embargo, si no se dispone de información sobre éstos, Ertur y Le Gallo (2009) sugieren especificar varianzas espaciales continuas a través de toda el área de estudio, y probar si la convergencia varía con la localización. Para ello se han empleado algunas técnicas que van desde una sencilla perspectiva de regímenes espaciales hasta métodos econométricos más complejos; siendo una de estas la regresión geográficamente ponderada (GWR, por sus siglas en inglés) (Brunsdon et al., 1996), la cual permite estimar parámetros locales y poner a prueba la heterogeneidad del proceso de convergencia a escala local (Bourdin, 2013; Eckey, Kosfeld y Tüeck, 2007).
Considerando que los estudios en relación con la heterogeneidad espacial del proceso de convergencia en México son escasos, y más aún aquellos que consideran una perspectiva municipal, el objetivo de este trabajo es poner a prueba, siguiendo un enfoque local, la hipótesis de convergencia-β (i.e. absoluta) y convergencia condicional para el período 1999-2014. En particular interesa saber: 1) si la convergencia local ocurrió en todos los municipios mexicanos, incluso con la presencia de variables de control, y/o si se observan patrones divergentes; 2) indagar si los municipios se mueven a diferentes velocidades hacia sus estados estacionarios localmente estables; y 3) describir el patrón espacial que se configuró en el periodo de estudio. Para ello, se utiliza el método GWR, el cual permite estimar parámetros locales. Así, el adjetivo “local” indica que cada municipio cuenta con sus propios parámetros estimados, a partir de los cuales se obtienen diferentes estados estacionarios y velocidades de convergencia; mientras que lo “regional” hace alusión al grupo de municipios involucrado en el proceso de convergencia local (i.e. el municipio bajo análisis y sus vecinos), a los cuales se les denomina microrregión.
Los principales resultados permiten dar respuesta a los objetivos específicos planteados en este estudio: 1) la evidencia muestra que los municipios mexicanos registran un proceso de convergencia local en el periodo 1999-2014 y en sus tres quinquenios, tanto de convergencia-β como condicional, identificándose algunos municipios en los cuales no se tiene suficiente evidencia empírica a favor de la convergencia; 2) se comprobó la no-estacionariedad del proceso de convergencia en todos los periodos analizados; y 3) el patrón de convergencia local apunta no solo a la presencia de múltiples estados estacionarios y velocidades, sino que también sugiere la polarización de los patrones de crecimiento tipo catching up, más allá de la visión tradicional de disparidades regionales Norte-Sur.
Para un análisis de la convergencia local, el trabajo se organiza de las siguientes secciones. En la sección 2 se revisan estudios empíricos que indagan sobre la heterogeneidad espacial y/o la no-estacionariedad del proceso de convergencia en México. La sección 3 resume el modelo de convergencia y su enfoque local, así como algunas consideraciones metodológicas, limitaciones y avances en la estimación de modelos de regresión geográficamente ponderados (GWR). La sección 4 contiene la descripción del conjunto de datos, fuentes de información y especificación de la estructura espacial empleada en este estudio. En la sección 5 se presentan los resultados de las estimaciones locales del modelo de convergencia absoluta y condicional, se muestra la evidencia de la no-estacionariedad del proceso y, posteriormente, se exploran los patrones espaciales. Finalmente, en la sección 6, se resumen los principales hallazgos y se concluye con algunas ideas clave sobre el proceso de convergencia en México.
1. La evidencia empírica de la convergencia en México
La investigación sobre convergencia del ingreso per cápita ha generado una gran cantidad de estudios y evidencia empírica. Los estudios pioneros de Barro y Sala-i-Martin (1992) y Sala-i-Martin (1994), para economías desarrolladas, demostraron que la convergencia-β fue sorprendentemente similar a una tasa de 2% anual, la cual se ha constituido en una regla empírica. Lo anterior implica que, pese a las diferencias en el crecimiento entre economías pobres y ricas, e independientemente de la escala geográfica y temporal de los estudios, todas las economías convergen hacia una única senda de crecimiento de largo plazo. Para Quah (1996), la consistencia del hallazgo sólo refleja un proceso mecánico (i.e. matemático) e independiente de la estructura económica de los países, puesto que ésta varía de muchas maneras, explicables e inexplicables, y a través de diferentes contextos. No obstante, el modelo de Barro y Sala-i-Martin (1995) se ha convertido en el modelo estándar para probar la hipótesis de convergencia.
En México, la dinámica de crecimiento económico registró un cambio estructural a raíz de la participación de este país en el Acuerdo General de Aranceles y Comercio (GATT, por sus siglas en inglés) en 1985, encontrándose evidencia de convergencia absoluta y condicional de 1970 a 1985, y en años posteriores la divergencia absoluta se desaceleró y la condicional se debilitó (Rodríguez, Mendoza y Venegas, 2016; Asuad y Quintana, 2010). Este comportamiento es similar al considerarse como punto de inflexión la entrada en vigor del Tratado de Libre Comercio de América del Norte (TLCAN) en 1995 (Díaz-Dapena et al., 2017; 2019; Rodríguez-Oreggia, 2005), el ingreso de China a la Organización Mundial de Comercio (OMC) en 2001 y la crisis financiera global de 2008 que causó un proceso de divergencia entre estados y una débil convergencia condicional en el corto plazo (Fonseca, Llamosas-Rosas y Rangel, 2019).
Si bien, la evidencia empírica que prueba la hipótesis de convergencia en México es amplia, se eligieron estudios con modelos que capturan, de alguna u otra manera, la heterogeneidad espacial a través de modelos no-estacionarios (tabla 1). En esta selección se incluyen, además, estudios con estimaciones convencionales para tener un referente en torno a la regla empírica del 2%. En general, los estudios seleccionados encuentran evidencia de convergencia entre grupos de estados relativamente homogéneos (i.e. clubes de convergencia); mientras que los estudios a escala municipal son escasos (excepto en Valdivia, 2012; Garduño, 2014; Rodríguez-Gámez y Cabrera-Pereyra, 2019; Díaz-Dapena et al., 2017; 2019).
Tabla 1 La evidencia empírica a favor de la convergencia regional en México
| Autor(es) | Método | Análisis espacial | Estacionariedad | Tasa de convergencia |
|---|---|---|---|---|
| Juan-Ramón y Rivera-Batiz (1996) | Transversal | Estados agrupados en pobres y ricos | No |
1970-1985 = 2.4% 1980-1993 = -1.6% |
| Esquivel (1999) | Transversal | Estados apilados en siete regiones | No | Si |
| Cermeño (2001) | Panel | Nivel estatal | No |
1970-1995 = 4.2% a 5.3% (diferentes periodos) |
| Díaz y Sáenz (2002) | Transversal | Estados agrupados cinco regiones | No | 1985- 1998 = 4% |
| Fuentes y Mendoza (2003) | Transversal | Nivel estatal | No |
1980-1985 = 4.8% 1985-1998 = - 1.4% |
| Ocegueda y Plascencia (2004) | Panel | Estados fronterizos (México-EE. UU.) | No | No sig. 5% |
| Rodríguez-Oreggia (2005) | Transversal | Estados agrupados en cuatro regiones | No |
1970-1985 = 4.1% 1985-2000 = 2.9% |
| Cermeño, Mayer y Martínez (2009) | Transversal | Municipios fronterizos (México-EE. UU.) | No |
No sig. (5%) en México Condados de EE. UU. |
| Valdivia (2012) | Econometría espacial | Municipios clasificados en centro y periferia | No |
3.1% (OLS) 3.0% (LAG) 1993-2003 = 3.6% (ERR) |
| Calderón y Tykhonenko (2007) | Panel | Estados | Si |
1994-2002 = 3.2% (tasa media estatal) |
| Valdivia (2008) | Econometría espacial | Región Centro (estados y municipios) | No | 1988-2003 = 3.5% |
| Díaz, Sánchez y Mendoza (2009) | Panel | Estados | No | 1970-2004 |
| Ruíz (2010) | Panel | Estados | No |
1900-2004 = 1.4% 1985-2004 = 2.1% |
| Asuad y Quintana (2010) | Econometría espacial | Estados | No |
1970-2006 = No sig. 5% 1970-1985 = 2.7% (MCO) 1986-2008 = No sig. 5% (LAG) |
| Rodríguez, Mendoza y Venegas (2016) | Panel TAR | Estados agrupados en regiones | No | Convergencia en 11 estados (más ricos) en 1970-2012. |
| Rodríguez, López y Mendoza (2016) | Panel de un factor (no-lineal) | Estados agrupados en regiones | No | Convergencia en 6 clubes (tasa entre 0 y 2%) de 1970-2012 |
| Díaz-Dapena, Fernández-Vázquez, Garduño-Rivera y Rubiera-Morollon (2017) | Panel | Municipios agrupados | No | 1 980-2010 = 1.6% 1980-1995 = 3.3% 1995-2010 = 1.5% |
| Díaz-Dapena et al., (2019) | Panel efectos fijos (Mundlak) | Municipios | Si | 1980-1993 = [-0.481 a - 0.113] |
| Rodríguez-Gámez y Cabrera-Pereyra (2019) | Econometría espacial | Municipios | No |
1999-2004 = 1.4% (ERR) 2004-2009 = 2.0% (ERR) 2009-2014 = 4.7% (ERR) 1999-2014 = 1.9 % (ERR) |
Fuente: elaboración propia en base a referencias citadas.
Nota: se refiere a estimaciones MCO = mínimos cuadrados ordinarios; ERR = errores espacialmente distribuidos; LAG = rezago espacial; TAR = autorregresivo de umbral y bootstrapping.
Los trabajos seleccionados en la tabla 1 son solo una muestra de la evidencia en México a favor de la convergencia, la cual es contrastante; no obstante, la convergencia-β oscila en torno a la regla empírica del 2% al analizar el largo plazo (Juan-Ramón y Rivera-Batiz, 1996; Esquivel, 1999; Ruíz, 2010). En cambio, las economías convergen a una tasa superior a la de referencia cuando se analiza el corto plazo (Ruíz, 2010; Rodríguez-Oreggia, 2005; Fuentes y Mendoza, 2003; Cermeño, 2001), al capturar la heterogeneidad espacial (Rodríguez-Gámez y Cabrera-Pereyra, 2019; Díaz et al., 2017; Asuad y Quintana, 2010; Valdivia, 2012 y 2008) y/o cuando el nivel de agregación de la información es el municipal (Rodríguez-Gámez y Cabrera-Pereyra, 2019; Díaz et al., 2017, 2019; Garduño, 2014; Valdivia, 2012 y 2008) (tabla 1).
En México el modelo de convergencia-β se ha utilizado ampliamente para estimar coeficientes de regresión estacionarios, que definen un comportamiento global o promedio para todas las observaciones (e.g. estados o municipios). La escasa evidencia en nuestro país de estudios de convergencia que estimen parámetros locales y, por tanto, no-estacionarios, no permite identificar la dinámica de crecimiento a escala local, de modo que los patrones espaciales del crecimiento a nivel municipal aún permanecen enmascarados; excepciones a lo anterior son los estudios de Calderón y Tykhonenko (2007) a nivel estatal y Díaz et al., (2019) a nivel municipal. Lo anterior revela una brecha de conocimiento, tanto teórico como empírico, en la que se sugiere trabajar para la comprensión de las dinámicas espaciales de crecimiento.
2. Crecimiento y convergencia en la perspectiva espacial
2.1 Crecimiento y convergencia económica
Una de las preguntas más importantes de la economía del crecimiento es si las regiones muestran un proceso de convergencia y, en consecuencia, de crecimiento equilibrado. La convergencia de ingresos entre países es ampliamente interpretada como una prueba al modelo de crecimiento neoclásico de Solow (1956). La convergencia ocurre cuando las economías de menores ingresos per cápita registran mayores tasas de retorno de capital y, en consecuencia, altas tasas de crecimiento económico, en relación con las economías de altos niveles de ingresos (i.e. efecto catch-up). Gran parte de la literatura empírica se basa en el modelo de Barro y Sala-i-Martin (1995), que pone a prueba la existencia de una relación negativa entre la tasa de crecimiento de los ingresos y su nivel inicial, teniendo como referente la ecuación 1.
Donde
Así,
Si los países o regiones bajo análisis son estructuralmente idénticos y estables en el tiempo (i.e. tienen una tasa similar y constante de ahorro, de depreciación, de crecimiento de la población y la misma función de producción), todas las economías convergerán hacia un mismo estado estacionario (i.e. situación de equilibrio estable de largo plazo). En contraste, si los países ricos crecen más rápido que los pobres (i.e. relación positiva), el modelo predice una divergencia y las desigualdades en el ingreso no sólo no desaparece, sino que aumentan con el tiempo (Sala-i-Martin, 1994). Por tanto, si la única diferencia entre economías es el nivel inicial de ingreso per cápita, se comprueba la hipótesis de convergencia absoluta (i.e. no condicional) o convergencia-β; así, entre más pobre la economía más rápido crecerá sobre su horizonte de largo plazo y, en consecuencia, las diferencias entre economías disminuyen con el tiempo.
Desde la lectura de Mankiw et al. (1992, 422), el planteamiento de Solow (1956) solo predice que el ingreso per cápita en un país dado converge al valor de estado estacionario de ese país. Por lo que, si la estructura de las economías difiere, pueden existir diferentes estados estacionarios y cada economía converge a su propio nivel de equilibrio. Dado que entre regiones de un país las estructuras productivas varían en muchos aspectos (i.e. tecnología, preferencias, instituciones, etc.), es difícil esperar que todas las economías converjan al mismo estado estacionario (Quah, 1996; Mankiw et al., 1992; Temple, 1999). En otras palabras, para cada tasa de ahorro y de capital habrá un estado estacionario, donde la única inversión es la de reposición; en consecuencia, se predice la convergencia después de controlar ciertas variables de inicio.
Así, cuando las economías difieren en su estructura y, por tanto, ya no comparten
un mismo estado estacionario, el proceso de convergencia es condicional. Dicho
de otra forma, la tasa de crecimiento
Las distintas condiciones de inicio surgen de diferencias en los acervos
iniciales de capital humano y en las directrices de política pública (Barro y Sala-i-Martin, 1995), pero lo que
subyace a estas diferencias son distintos “regímenes” o “clubes” de convergencia
(Durlauf y Johnson, 1994; Quah, 1996; Galor, 1996; Baumol, 1986). Así, los efectos derivados de
En este sentido, Bloom et al. (2002) y Durlauf, Kourtellos y Tan (2005b) sugieren que, al considerar modelos con múltiples equilibrios, se evalue la no-estacionariedad espacial de los parámetros. Siguiendo a Fotheringham et al. (1997; 1998) existen, al menos, tres razones por las cuales los parámetros pueden variar en el espacio: 1) hay cierta no-estacionariedad espacial causada por variaciones aleatorias existentes en las áreas de estudio; 2) algunas de las relaciones analizadas son intrínsecamente diferentes; y 3) los modelos lineales, con estimaciones de mínimos cuadrados ordinarios (MCO) no miden las interacciones espaciales y, por lo general, una o más variables relevantes se omiten o su forma funcional es incorrecta. Así, la tasa de convergencia y la de otros determinantes del crecimiento varían de una región a otra.
2.2 El enfoque local
En medio del debate con relación al crecimiento equilibrado (enfoque neoclásico) y desequilibrado (teoría de la causación circular), se encuentra la nueva teoría del crecimiento que apoya la idea de múltiples equilibrios, así como la coexistencia de procesos de convergencia y divergencia (Capello, 2009; Artelaris, 2015). Desde el punto de vista metodológico se presentan tres tipos de modelos: el global, el de regímenes y el local. En los modelos globales, que han estado influenciados por el paradigma neoclásico, se estima un solo parámetro “global” para definir el proceso de interacción entre observaciones (e.g. regiones) (Brunsdon et al., 1996), asumiéndose una relación estable, entre variables, a través del espacio (i.e. homogeneidad espacial). Sin embargo, los modelos globales no son capaces de captar y explicar los patrones relacionados con la dimensión espacial de la no-estacionariedad (Getis, 2007).
Al considerarse la existencia de múltiples equilibrios, la relación global podría no ser válida en toda el área de estudio (Quah, 1996); de ahí que la hipótesis de múltiples equilibrios requiera de la identificación de regímenes o “clubes” de regiones, a través de las cuales los parámetros pueden variar, mientas que al interior de cada una de estas se presenta un comportamiento global: clubes de convergencia . Lo anterior sugiere que la convergencia no es un fenómeno “amplio” y ésta puede ocurrir, solo, en un grupo de economías que comparten ciertas características estructurales (Beaumont, Ertur y Le Gallo, 2003; Durlauf y Johnson, 1994; Quah, 1996; Galor, 1996; Baumol, 1986). Dicha situación es congruente con el paradigma neoclásico y el modelo tradicional de convergencia (Chatterji y Dewhurst, 1996; Galor, 1996).
Siguiendo esta línea, la existencia de múltiples equilibrios implica que la convergencia puede ser, efectivamente, un fenómeno “amplio”, presente en todo el espacio analizado, pero teniendo en cuenta un ámbito “local” y no uno “global”: los parámetros de regresión pueden variar de una región a otra y no solo entre grupos de regiones. Con fundamento en la Primera Ley de la Geografía: “todo está relacionado con todo lo demás, pero las cosas cercanas están más relacionadas que las distantes” (Tobler, 1970, 236), cada región puede converger a su propio estado estacionario de equilibrio, localmente estable, mientras que la velocidad a la cual converge se determina, conjuntamente, entre sus vecinos. Ello implica la estimación de parámetros para cada región y el descubrimiento de patrones ignorados por modelos globales.
Así, la convergencia local se define como el estado de convergencia (i.e. disminución de las disparidades económicas) entre regiones cercanas, de ahí que no solo las condiciones económicas iniciales, sino también la proximidad geográfica, influyen en la convergencia (Bourdin, 2013). Al respecto, Galor (1996) ofrece una discusión teórica sobre la multiplicidad de equilibrios de estado estacionario, previstos por el paradigma neoclásico.1 Por ello, la convergencia local puede ser tanto absoluta (i.e. los ingresos per cápita regional converge entre sí a largo plazo, independientemente de sus condiciones iniciales), como condicional (i.e. convergencia incluso si los ingresos per cápita son idénticos en sus características estructurales).
Uno de los métodos locales de estimación utilizado para el análisis de
convergencia es la regresión geográficamente ponderada (GWR) (Brunsdon, Fotheringham y Charlton, 1998 y
1996; Fotheringham et al., 1998). Este método es una
técnica relativamente sencilla y eficaz para explorar la no-estacionariedad
espacial (Fotheringham et al.,
1998) y descubrir complejas variaciones espaciales
(i.e. patrones) al mapear los parámetros locales (Brunsdon et al., 1996). La
GWR permite variaciones locales de los parámetros, de modo que los coeficientes
en lugar de ser estimaciones globales son específicos para una ubicación
Los parámetros locales se estiman, para cada lugar
De acuerdo con lo anterior,
Suponiendo que los parámetros presentan cierto grado de coherencia espacial
(Primera Ley de la Geografía), entonces los valores cercanos al lugar
2.3 Limitaciones y avances del enfoque GWR
El enfoque GWR ofrece ventajas significativas sobre la regresión lineal simple,
tales como la apropiada asignación y fácil visualización de los coeficientes de
regresión locales (Wheeler y Tiefelsdorf,
2005; Fotheringham et
al., 2002), así como su capacidad para explicar más
variación que las estimaciones por MCO (Ogneva-Himmelberger, Pearsall y Rakshit, 2009). Incluso existen
ventajas de la estimación GWR sobre los modelos espaciales Durbin
(i.e. modelos espaciales autorregresivos y de dependencia
espacial anidada de los errores), ya que la influencia espacial se calibra a
partir de los datos; mientras que en un modelo espacial los efectos se capturan
en la matriz de pesos
Sin embargo, la literatura señala que las estimaciones con GWR son, en parte, dependientes de la función de ponderación y sensibles a la selección del ancho de banda, aspectos que pueden generar problemas de precisión en la estimación (Wheeler y Tiefelsdorf, 2005; LeSage, 2014). Estas limitantes continúan siendo parte de las discusiones de los modelos GWR y fuente de desarrollo de métodos de mejoramiento del cálculo de parámetros locales (consúltese Propastin, Kappas y Erasmi, 2008; Lu, Charlton, Harris y Fotheringham, 2014; y Billé et al., 2017). No obstante, se reconocen dos implicaciones importantes: 1) cómo saber si el modelo GWR describe mejor las observaciones que un modelo MCO; y 2) si bien el modelo GWR detecta la presencia de heterogeneidad espacial, éste no la explica del todo, ni tampoco la significancia de los parámetros estimados (Billé et al., 2017; Leung, Mei y Zhang, 2000).
En relación con la primera implicación, la selección del modelo (GWR
vs. MCO) se relaciona con el ancho de banda (Fotheringham, 2009). Para ello se
contrastan y comparan los valores del Criterio de Información de Akaike
Para el caso del modelo MCO, el estimador
Considerando la segunda implicación, en relación con la significancia de
parámetros y la validez de la detección de la heterogeneidad espacial, la
literatura sugiere utilizar la desviación de cada parámetro estimado
(e.g.
En cambio, Leung et al., (2000)
desarrollaron una serie de pruebas, en base al estadístico
Segundo, se construye una prueba
Finalmente, Leung et al., (2000, 21)
proponen una tercera prueba
Si bien el método GWR permite explorar la estructura de la heterogeneidad
espacial de las variables y mejora la estimación de los parámetros (Farber y Yeates, 2006), existe en éste un
intercambio (“trade-off”) entre “precisión de predicción y
complejidad” del modelo (Lu et
al., 2014, 3). En consecuencia, las pruebas de
significancia y de bondad de ajuste (e.g.
3. Notas metodológicas
3.1 Datos y fuentes de información
Las variables clave para poner a prueba la hipótesis de convergencia-β son la
tasa anual de crecimiento económico municipal
El VACB es el valor de la producción que se añade durante el proceso de trabajo
por la actividad creadora y de transformación del personal ocupado, el capital y
la organización (i.e. factores de la producción), ejercida
sobre los materiales que se consumen durante la actividad económica; este valor
es bruto ya que no se le ha deducido el consumo de capital fijo (Inegi, 2015a, 76). En base a esta
información se obtiene el valor agregado per cápita (VAPC), como
proxy del nivel de ingreso (
Un problema metodológico a considerar es el registro negativo del VACB (i.e. consumo intermedio superior a los ingresos generados) en algunos municipios, los cuales representan, aproximadamente el 1% del total nacional.3 Al respecto se decidió no excluir del análisis a estos municipios (como en Díaz-Dapena et al., 2019) o sustituir sus valores por cero (del modo que sugiere CEDRUS, s.f., 11), ya que teóricamente el proceso de apalancamiento negativo de estas economías es parte integral del enfoque de regímenes espaciales. Además, desde la perspectiva espacial es relevante no ignorar ninguna unidad espacial y capturar, precisamente, ese efecto de arrastre hacia abajo; en tal caso, la presencia de estas economías de “subsistencia” en una vecindad representa un contrapeso local, cuyo efecto favorece procesos de convergencia descendente (downward convergence) (Ben-David, 1998; Kraay y McKenzie, 2014).
Esta decisión requirió atender el problema de la transformación logarítmica de
valores negativos, en tales casos se procedió a estimar el logaritmo natural
Otra consideración importante, para dimensionar los hallazgos del estudio, son las discrepancias metodológicas entre PIB y VACB. Pese a que la información no es comparable, ambos indicadores se utilizan para divulgar aspectos relevantes del acontecer económico, pero una no tiene preeminencia sobre la otra (Inegi, 2010b, 8). La naturaleza de tales diferencias son: 1) de cobertura, ya que el CE excluye ciertas actividades económicas como las agropecuarias, los servicios educativos, de salud y de administración pública y defensa (al no asignarles un valor, dada su lógica privada de provisión), y las actividades informales, entre otras; y 2) metodológicas, ya que el ordenamiento contable del CE tiene un enfoque microeconómico empresarial (i.e. precios del productor), mientras que el cálculo del PIB se basa en el costo de oportunidad (i.e. precios de mercado), diferencia que estriba en la consideración de impuestos y subsidios aplicable a la contabilidad nacional (Inegi, 2010b, 7-8).
Pese a que la información del VACB cuenta con una cobertura más limitada que el PIB y está valorada a precios de productor, el uso de esta información tiene la ventaja de saber, con mayor precisión, cuánto valor es agregado por un municipio y su contribución a la economía nacional. Lo anterior gracias a que, para las actividades manufactureras, comerciales y de servicios, la unidad de observación es el establecimiento (definidos bajo el control de una sola entidad propietaria y asentados permanentemente); así, la información obtenida está referida a la ubicación donde realmente se lleva a cabo la actividad (Inegi, 2015, 11).5
En el caso de la estimación del modelo de convergencia condicional, la
construcción de los componentes
En el caso del vector
Finalmente, siguiendo las recomendaciones de Barro y Sala-i-Martin (1995), se incluye la inversión pública
federal ejercida, en términos per cápita, como parte del vector
3.2 Especificación de la estructura espacial
El VAPC entre los municipios de México y su tasa de crecimiento son indicadores
de naturaleza espacial (Rodríguez-Gámez y
Cabrera-Pereyra, 2017), por lo que la posibilidad de que la tasa de
convergencia estimada sea también una variable espacial y, en consecuencia,
varíe a través de los municipios (i.e. heterogeneidad espacial)
es una situación altamente probable. Por ello, es necesario introducir una
estructura espacial apropiada que modele la interacción entre municipios y
detecte la no-estacionariedad. Nos referimos al ancho de banda
(i.e. amplitud o distancia en donde a partir del núcleo
Si no se dispone de información previa sobre los regímenes espaciales Ertur y Le Gallo (2009) sugieren utilizar una varianza espacial continua a través de la zona de estudio o definir, a priori, la forma de propagación de los efectos espaciales entre observaciones (e.g. contigüidad binaria). No obstante, predefinir una estructura espacial resulta restrictivo, ya que se requiere información, de antemano, de dicha estructura (Ibragimov y Müller, 2010). En este sentido, los modelos GWR son una “alternativa” útil y una “herramienta de diagnóstico” para la correcta detección de la heterogeneidad espacial (Billé et al., 2017, 455). Así, cuando las observaciones no están distribuidas de manera uniforme, a través del área de estudio, la literatura sugiere una función de Gauss ponderada, con un ancho de banda que se adapte a cada núcleo (i.e. adaptative kernel) (Fotheringham et al., 2002; Fotheringham, 2009; Páez, Farber y Wheeler, 2011).
El uso de un ancho de banda dinámico permite que los núcleos varíen espacialmente, siendo menor la variación en las regiones donde la densidad de datos (i.e. número de municipios) es alta y más grande donde la densidad de datos es baja (Fotheringham et al., 2002). Para un ancho de banda dinámico, la amplitud se calcula en función de la densidad de puntos de datos, obteniéndose el número de observaciones según la distancia euclidiana entre los centroides de las áreas municipales; en la cual los municipios más próximos ejercen mayor influencia y ésta disminuye conforme el radio de influencia aumenta. En consecuencia, tanto el número efectivo de parámetros, como los grados de libertad de la estimación, varían según el ancho de banda.
En el caso de México, la base de datos se conformó por 2,491 municipios para el periodo 1999-2014.6 El promedio de observaciones vecinas (i.e. tamaño del subconjunto de municipios) para cada modelo estimado fue de 38 observaciones, las cuales representa, aproximadamente, el 1.5% de los municipios del país. Sin embargo, la amplitud del ancho de banda varia notablemente de una región a otra; por ejemplo, en la región Centro del país el ancho de banda oscila entre 19.1 y 60 km, mientras que en la península de Baja California llega a más de 700 km (figura 1). Estos datos sustentan la pertinencia de establecer un ancho de banda dinámico, para la estimación local, en función del tamaño y la proximidad de los municipios.
Finalmente, con las variables definidas, se construyó una base datos para el
cálculo de las estimaciones locales del modelo de convergencia-β y condicional
en el Software R (R Core Team,
2018), la cual se geo-referencio con el Software
ArcMap (v.10.2.2). El método GWR se implementó a través del paquete
“spgwr” (Bivand y Lu,
2020), diseñado para ejecutarse en el software estadístico
R. Con este software se estimaron también los estadísticos
4. Explorando la no-estacionariedad del proceso de convergencia
4.1 Convergencia absoluta
Partiendo de un análisis convencional de MCO, se obtiene un coeficiente β negativo y estadísticamente significativo para el nivel de ingreso per cápita inicial (LNVAPC) en cada uno de los periodos estudiados (tabla 2). Con ello se comprueba la hipótesis de convergencia-β (i.e. absoluta) en el periodo 1999-2014: los municipios mexicanos con menores niveles de LNVAPC crecieron más rápido que aquellos de alto LNVAPC, en consecuencia, los niveles de ingreso convergen entre sí a largo plazo, a una velocidad de 2.1%; de tal manera que les tomaría 33 años en superen la mitad de la distancia que les separa del estado estacionario.
Para indagar sobre la no-estacionariedad se realiza un cambio de enfoque, del
“global” al “local”, con la aplicación de GWR. La tabla 2 resume las estimaciones de los parámetros locales
Sin embargo, algunos municipios registraron una tasa local de convergencia mayor
o menor que la tasa global. Considerando las estimaciones locales que son
estadísticamente significativas al 99% (valores de
En la tabla 2 se presentan también los
valores “cuasi-globales” de
Los valores del estadístico
Tabla 2 Análisis comparativo de los parámetros estimados de convergencia absoluta con MCO y GWR
| Modelo estadístico | 1999-2004 | 2004-2009 | 2009-2014 | 1999-2014 | |||||
|---|---|---|---|---|---|---|---|---|---|
| a | β | a | β | a | β | a | β | ||
| Estimación por MCO (parámetros globales) | |||||||||
| Parámetro | 0.1208 | -0.0216 | 0.0693 | -0.0378 | 0.1256 | -0.0472 | 0.0855 | -0.0180 | |
| Estado estacionario (a|β) | 5.9 | 1.8 | 2.6 | 4.8 | |||||
| Tasa de convergencia | 2.2% | 3.8% | 4.7% | 1.8% | |||||
| Velocidad de convergencia | 2.3% | 4.2% | 5.4% | 2.1% | |||||
| Media-vida | 31.7 | 18.0 | 14.3 | 33.3 | |||||
|
|
4.4% | 11.4% | 16.8% | 19.0% | |||||
|
|
- 1,511.57 | - 1,160.58 | - 1,357.94 | - 6,480.8 | |||||
| Estimaciones con GWR (parámetros locales) | |||||||||
| Parámetro β | Mínimo | -0.0053 | -0.0789 | -0.0585 | -0.1387 | 0.0204 | -0.1279 | 0.0510 | -0.0390 |
| 1er. Cuartil (25%) | 0.0957 | -0.0387 | 0.0366 | -0.0605 | 0.0925 | -0.0753 | 0.0714 | -0.0247 | |
| Mediana (50%) | 0.1229 | -0.0299 | 0.0527 | -0.0372 | 0.1136 | -0.0552 | 0.0843 | -0.0202 | |
| 3er. Cuartil (75%) | 0.1465 | -0.0224 | 0.0779 | -0.0187 | 0.1536 | -0.0429 | 0.0978 | -0.0165 | |
| Máximo | 0.1988 | 0.0006 | 0.1797 | 0.0050 | 0.3580 | -0.0128 | 0.1246 | -0.0079 | |
| Rango Inter-cuartil | 0.0508 | 0.0163 | 0.0413 | 0.0418 | 0.0611 | 0.0324 | 0.0264 | 0.0082 | |
| Parámetro β (promedio) | 0.1208 | -0.0216 | 0.0694 | -0.0378 | 0.1256 | -0.0472 | 0.0825 | -0.0209 | |
| Parámetros significativos (% del total) | 94.1% | 68.8% | 62.3% | 64.9% | 94.1% | 92.8% | 100.0% | 98.2% | |
|
|
14.6% | 25.4% | 28.9% | 26.1% | |||||
| Estado estacionario (promedio) | 3.7 | 5.4 | 4.5 | 4.4 | |||||
| Tasa de convergencia (promedio) | 2.2% | 3.8% | 4.7% | 2.1% | |||||
| Velocidad de convergencia (promedio) | 4.1% | 7.2% | 7.6% | 2.6% | |||||
| Media-vida (promedio) | 20.3 | 14.4 | 12.2 | 30.2 | |||||
| Pruebas de estacionariedad y heterogeneidad de los parámetros estimados | |||||||||
| Prueba |
0.9481* | 0.8968*** | 0.9050*** | 0.9793 | |||||
| Prueba |
2.2766*** | 3.3477*** | 2.5794*** | 2.0829*** | |||||
| Prueba |
4.6833*** | 3.6509*** | 5.9920*** | 5.0425*** | |||||
| β | 1.8104*** | 8.3293*** | 3.0371*** | 3.3587*** | |||||
|
|
- 1,603.5 | - 1,401.7 | - 1,546.7 | ||||||
Fuente: Elaboración propia.
Nota: todos los parámetros estimados tienen significancia del 99%, para las pruebas F: * (0.05), ** (0.01) y *** (0.001). Para las estimaciones MCO y GWR se utilizó el Software (R Core Team, 2018).
Como ha sido sugerido en la literatura (Fotheringham et al., 2002; Leung et al., 2000), se pone a prueba la
no-estacionariedad. Así, a través de la prueba
En la figura 2 (sección izquierda), se observa que el rango intercalase de la velocidad de convergencia, en el periodo 1999-2014, oscila entre 0.8% y 5.9%. Los municipios con bajas velocidades de convergencia, entre 0.8% y 1.8%, y que converge más lentamente que el resto de municipios a su estado estacionario “locamente estable”, se localizan en al menos tres regiones: 1) Centro-norte, municipios en Sinaloa, extremo sur de Chihuahua, Durango, al sur de Coahuila, centro y sur de Nuevo León, centro y norte de Tamaulipas, Zacatecas y norte de San Luis Potosí; 2) Centro, municipios en Michoacán, Guanajuato, Querétaro, Estado de México, Ciudad de México, Morelos y norte de Guerrero; y 3) Golfo, integrada por Tabasco y municipios colindantes con Veracruz, Chiapas y Campeche (figura 2, izquierda).
Por otra parte, altas velocidades de convergencia, entre 4.5% y 5.9%, se registraron en: 1) Oaxaca, en municipios de la región Mixteca y en la región Sierra Norte; y 2) en la Península de Yucatán, en los municipios colindantes entre Campeche (municipios colindantes con Yucatán), Yucatán (con excepción de los municipios de la región de Influencia Metropolitana y en la del Litoral Oriente) y Quintana Roo (Felipe Carrillo Puerto y José María Morelos) (figura 2, izquierda). Se observa que las regiones conformadas por este tipo de municipios no conforman una zona continua, como en el caso de los municipios de baja velocidad de convergencia, en cambio son aglomeraciones de municipios con un rápido crecimiento a escala microrregional. Así, a los municipios con baja velocidad les tomaría 49.4 años, en promedio, el cubrir la mitad de la variación de ingreso que los separa de su estado estacionario localmente estable; mientras que a los de más alta velocidad de convergencia les tomaría solo 14.4 años.

Fuente: Elaboración propia.
Nota: La clasificación de datos sigue sus cortes naturales (Jenks).
Figura 2 Velocidad municipal de convergencia-β a su estado estacionario (localmente estable) (1999-2014)
Los resultados sugieren la existencia de regímenes espaciales o clubes de convergencia entre los municipios de México. La polarización entre patrones de crecimiento indica dos grandes procesos. Por un lado, las velocidades de convergencia del núcleo o centro de municipios con bajos valores (de 1.7% y menores) son más bajas que las de su periferia (i.e. los municipios que los rodean, con tasas de entre 1.8% y 2.3%) y más bajas aún (de 2.4% a 2.9%) que el siguiente grupo de municipios circundantes; esto indicaría que el proceso de apalancamiento (catching-up) ya es más desacelerado a nivel local. Por otro, las velocidades de convergencia del núcleo o centro de los municipios con altos valores (mayores a 4.5%) son más altas que las de su correspondiente periferia (municipios con velocidades de 3.7% a 4.4%) y éstas a su vez son menores (de 3.0% a 3.6%) hacia el siguiente grupo de municipios adyacentes, lo cual indica una fuerza de arrastre o apalancamiento local en pleno auge.
Así, la heterogeneidad del proceso implica la existencia de múltiples
equilibrios. Bajo el enfoque local, cada municipio converge, a largo plazo y a
diferentes velocidades, a un determinado nivel de ingreso en estado estacionario (
Se observa (figura 2, derecha) que los niveles “locales” de ingreso (LNVAPC) en estado estacionario de las economías pobres (e.g. en Oaxaca), registran mayores velocidades de convergencia, asimismo éstas se encuentran por debajo del nivel “global” de estado estacionario (4.8 en el periodo 1999-2014), de ahí que converjan más rápidamente a su nivel local ya que se encuentran alejadas de este punto; mientras que los municipios ricos, con menor velocidad de convergencia, tienen estados estacionarios “locales” por encima del valor “global” (tabla 2 y figura 2). Así, los mayores niveles de estado estacionario se localizaron en municipios de Durango y la región del Sombrerete en Zacatecas, en Nuevo León y Tamaulipas, y en el Centro de país (municipios colindantes entre Michoacán y Guanajuato; así como al poniente del área metropolitana de la Ciudad de México); en contraste, podemos observar municipios con bajos niveles en el centro de la Península de Yucatán, en el área central de Chiapas, en la región Mixteca de Oaxaca y en municipios colindantes a ésta en Guerrero y Puebla, municipios al norte de Hidalgo y sur de San Luis Potosí, así como al norte de Puebla, (figura 2, derecha).
En el corto plazo (i.e. 1999-2004, 2004-2009 y 2009-2014) se
observó, también, una heterogeneidad en el proceso de convergencia, el valor y
significancia de la prueba
En el segundo quinquenio (2Q: 2004-2009) la velocidad de convergencia llegó a
23.7%, los valores más altos se registraron en Manzanillo y municipios contiguos
en Colima y Jalisco; así como en la región Mixteca de Oaxaca, que registró los
valores máximos (figura 3). En 2Q se
registraron mayores velocidades y emergió un patrón espacial distinto: los
municipios, con valores no significativos o de bajas velocidades, al Sur-sureste
del país en 1Q, se acercaron más rápido a su estado estacionario en 2Q, con
excepción de algunos municipios en Durango; asimismo, para una amplia zona en el
Centro del país no se obtuvo suficiente evidencia estadística para aceptar la
hipótesis de convergencia-

Fuente: Elaboración propia.
Nota: La clasificación de datos sigue sus cortes naturales (Jenks). Parámetros estadísticamente significativos al 99%.
Figura 3 Velocidad municipal de convergencia-β a su estado estacionario (localmente estable) (1999-2004, 2004-2009 y 2009-2014)
Estos hallazgos, que apoyan la existencia de múltiples estados estacionarios locales y no necesariamente uno solo de carácter global, son consistentes con la presencia de clubes de convergencia (Galor, 1996; Quah, 1996; para análisis empírico, Beaumont et al.,2003; Phillips y Sul, 2009). Si bien la literatura expresa la necesidad de hacer más pruebas empíricas antes de asumir, con cierto grado de confiabilidad la existencia de clubes de convergencia, los resultados de los modelos GWR son, en sí, un excelente diagnóstico sobre la posible naturaleza y dinámica espacial heterogénea de los múltiples equilibrios. En este sentido, los resultados se alinean a la propuesta de Beaumont et al. (2003), a favor del uso de modelos espaciales para la adecuada detección de patrones heterogéneos de crecimiento.
4.2 Convergencia condicional
En el enfoque convencional de convergencia, la multiplicidad de estados
estacionarios de equilibrio es posible debido a una dotación diferenciada de
factores productivos (e.g. capital) y tasas de ahorro; así, el
reconocimiento de distintas condiciones de inicio implica que las economías ya
no comparten un mismo estado estacionario (Galor, 1996). De ocurrir la convergencia ésta será condicional: se
espera que el efecto de alcance de las economías atrasadas se dé, inclusive,
pese a las diferencias estructurales. Bajo el enfoque local, la convergencia
condicional implica que dicha expectativa se dé a nivel microrregional (entre el
municipio
En la figura 4 se despliega los resultados
de las estimaciones GWR para el modelo condicional (veáse ecuación 2). En base a esta
información se corrobora la hipótesis de convergencia condicional local en el
periodo 1999-2014 (i.e.
El intercepto resultó no significativo en la región Centro del país: Ciudad de
México, Estado de México, Morelos, Puebla, Tlaxcala, Hidalgo y municipios
contiguos a esta área en los estados de Oaxaca, Veracruz, San Luis Potosí,
Querétaro, Guanajuato, Michoacán y Guerrero (figura 4). Por otro lado, el parámetro

Fuente: Elaboración propia.
Nota: La clasificación de datos sigue sus cortes naturales (Jenks). Parámetros estadísticamente significativos al 95%, para π5 la significancia es de 90%.
Figura 4 Velocidad de convergencia condicional y estimación de parámetros locales entre municipios de México (1999-2014)
Las variables de control tienen el signo esperado y son estadísticamente
significativas al 95%, con algunas excepciones según los resultados desplegados
en la figura 4. Las condiciones económicas
En el caso de las condiciones de desarrollo
La contribución de LNSOCPC99 (
Las pruebas de bondad de ajuste (
Tabla 3 Pruebas F y de heterogeneidad de parámetros en modelos GWR condicionales
| Parámetro | 1999 - 2004 | 2004 - 2009 | 2009 - 2014 | 1999 - 2014 |
|---|---|---|---|---|
| Pruebas de bondad de ajuste | ||||
|
|
27.4% | 25.2% | 34.2% | 30.5% |
|
|
0.9664 | 0.9346** | 0.9429* | 0.9793 |
|
|
2.1739*** | 3.1389*** | 2.8820*** | 2.086*** |
| Prueba de heterogeneidad de
parámetros ( | ||||
|
|
2.7067*** | 2.7774*** | 3.7121*** | 2.3216*** |
|
|
1.6551*** | 22.2261*** | 7.5778*** | 3.6154*** |
|
|
1.2206 | 1.6333* | 0.6665 | 0.3096 |
|
|
2.6257*** | 6.6771*** | 5.9728*** | 5.2066*** |
|
|
2.6542*** | 3.5422*** | 2.8042*** | 2.7428*** |
|
|
2.1581*** | 1.5932*** | 1.9821*** | 2.2865*** |
|
|
1.0982 | 2.3631*** | 3.0384*** | 0.8554 |
|
|
1.0235 | 0.1345 | 0.2043 | 0.4481 |
|
|
0.8760 | 0.3959 | 0.5901 | 0.2476 |
Fuente: para las estimaciones MCO y estimaciones del modelo GWR se utilizó el Software R (R Core Team, 2018).
Nota: significancia estadística de * (0.05), ** (0.01) y *** (0.001).
La heterogeneidad de los parámetros implica que existen diferencias espaciales en
el crecimiento económico municipal y en el proceso de convergencia, como
consecuencia de la acción del gobierno y de los agentes económicos locales, así
como por las condiciones geográficas y de localización de un municipio en
particular. Los resultados que se muestran en la figura 4, refuerza la pertinencia del uso de estimaciones GWR: en el
caso del proceso de convergencia condicional (1999-2014) es posible reconocer un
patrón espacial que distingue entre Norte y Sur, pero sin que esto signifique un
proceso lineal, en donde el Sur está creciendo más rápidamente (mayor velocidad)
y cuyo núcleo crece a tasas más aceleradas (4.9% a 5.2%) que su periferia (4.6%
a 4.8%) y la zona más allá de ésta (4.2% a 4.5%), lo que hace suponer que existe
un efecto de apalancamiento o arrastre espacial detectado por los modelos
locales. No obstante, se identifica un segundo núcleo (Centro-norte del país)
donde la velocidad de convergencia es menor (3.3% a 3.7%) a la de su periferia
(3.8% a 4.1%), lo que implica un apalancamiento desacelerado. A diferencia del
patrón geográfico de los modelos locales de convergencia-
A nivel de quinquenio, los resultados permiten argumentar que la convergencia
condicional se reforzó con el tiempo: el grado de respuesta del crecimiento
promedio del LNVAPC (
En 1Q el patrón espacial a favor de la convergencia tiene un núcleo de valores altos en el Centro del país, a partir del cual disminuye el efecto catching-up; sin embargo, en la Península de Yucatán y en el Noroeste se observa un incremento de las velocidades de convergencia que permiten identificar dinámicas de crecimiento en auge. El patrón espacial en 2Q tiene su núcleo en Oaxaca (región Mixteca y costa del estado), con velocidades mayores y un proceso de apalancamiento que se desacelera hacia la periferia; pero, de nuevo, en la región Noroeste se estuvo conduciendo una dinámica de crecimiento superior a la de su propia periferia. En el último quinquenio (3Q), la diferenciación entre Norte y Sur es más evidente, el núcleo se localiza en Oaxaca y se registran menores velocidades de convergencia en la periferia, la cual se extiende por el territorio, incluida la región Noroeste, con excepción de la Península de Yucatán en donde el proceso de apalancamiento se acelera (figura 5).
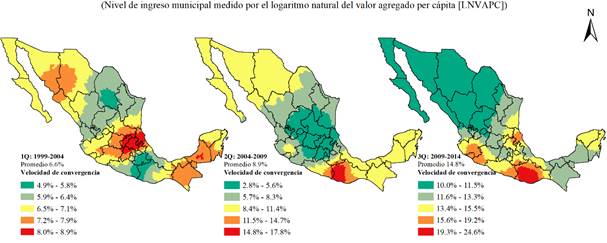
Fuente: Elaboración propia.
Nota: La clasificación de datos sigue sus cortes naturales (Jenks). Parámetros estadísticamente significativos al 99%.
Figura 5 Velocidad municipal de convergencia condicional localmente estable (1999-2004, 2004-2009 y 2009-2014)
En contraste con la estimación del periodo 1999-2014, las variables de control de
los modelos locales de convergencia condicional por quinquenio mostraron una
contribución diferenciada; además de que algunas resultaron estadísticamente
significativas solo en unos cuantos municipios (véase tabla 4). Dada la riqueza de resultados y la diversidad de
análisis que se derivan de esta información, solo se resaltará la contribución
de las variables con parámetros no-estacionarios, de acuerdo con la prueba
Tabla 4 Valor promedio de los parámetros locales en modelos quinquenales de convergencia condicional
| 1Q: 1999 - 2004 | 2Q: 2004 - 2009 | 3Q: 2009 - 2014 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Parámetro | Promedio | % Municipios | Min. Max. | Promedio | % Municipios | Rango | Promedio | % Municipios | Rango |
|
|
-0.1134 | 19.6% | -0.1921+0.0859 | 0.2130 | 54.4% | +0.1080+0.4077 | -0.7139 | 89.4% | -1.2924-0.0791 |
|
|
-0.0562 | 100.0% | -0.0718-0.0436 | -0.0695 | 100.0% | -0.1180-0.0262 | -0.1032 | 100% | -0.1416-0.0785 |
|
|
1.3274 | 45.3% | +0.6788 +2.2260 | -2.0044 | 39.3% | -3.3727 -0.9159 | --- | 0.0% | --- |
|
|
0.0007 | 54.6% | +0.0002 +0.0014 | 0.0015 | 74.7% | +0.0005 +0.0030 | 0.0061 | 100% | +0.0021 +0.0102 |
|
|
0.4361 | 84.4% | +0.1895 +0.7462 | -0.0340 | 38.3% | -0.0591 +0.0376 | 1.1177 | 82.6% | +0.4457 +1.9661 |
|
|
0.1815 | 36.3% | +0.1119 +0.2492 | 0.0197 | 56.7% | +0.0087 +0.0350 | 0.1681 | 23.1% | +0.0757 +0.2793 |
|
|
-0.3938 | 89.7% | -0.5671 -0.0216 | -0.5955 | 93.0% | -1.3820 -0.3107 | -0.4588 | 69.0% | -0.9540 -0.1795 |
|
|
-0.0681 | 5.8% | -0.1028 -0.0537 | -0.0996 | 0.2% | -0.1012 -0.0983 | -0.0550 | 3.0% | -0.0627 -0.0407 |
|
|
0.1679 | 11.5% | +0.0959 +0.2619 | 0.0808 | 5.9% | +0.0615 +0.0922 | -0.0663 | 40.3% | -0.1125 +0.0656 |
Nota: Promedios para municipios con parámetros estadísticamente significativos. El nivel de significancia estadística corresponde al 95%.
Fuente: para las estimaciones MCO y estimaciones del modelo GWR se utilizó el Software R (R Core Team, 2018).
Conclusiones
El comportamiento de los agentes económicos locales y las acciones de gobierno, así como la capacidad de los municipios vecinos de adaptarse y los efectos locales de la interacción entre estos, se refleja en parámetros localmente diferenciados en el proceso de convergencia. Sin embargo, este hecho se ignora al adoptarse un enfoque global en los modelos de crecimiento, por lo que el supuesto de estacionariedad contrasta fuertemente con la realidad local. Así, con el ánimo de encontrar respuestas más convincentes a las interrogantes planteadas en el ámbito de la economía regional y contribuir a delinear acciones de política pública, se puso a prueba la convergencia en el crecimiento económico municipal, adoptándose un enfoque local, capturando la no-estacionariedad de la dinámica económica a través del espacio geográfico.
La aplicación del enfoque local muestra, en resumen, los siguientes hallazgos. Primero, la evidencia empírica muestra que, en el caso de economías municipales homogéneas, cada una converge a su nivel de estado estacionario (localmente estable), durante el periodo 1999-2014 y en sus tres quinquenios; incluso, en función de ciertos factores endógenos que determinan las condiciones de inicio, la convergencia local se presentó como un fenómeno ampliamente extendido en el territorio y registró un proceso de reforzamiento en el tiempo. Este resultado es congruente con una mayor dinámica económica tras la recuperación de la crisis financiera global del 2008; así, las disparidades disminuyeron más rápido en el último quinquenio.
Segundo, en congruencia con el enfoque local, se comprobó la no-estacionariedad del proceso de convergencia en todos los periodos de estudio. Sin embargo, en el periodo 2004-2009 se observó un mayor número de municipios sin evidencia suficiente a favor de la convergencia local. Lo anterior implica que los municipios se mueven a diferentes velocidades y en distintas direcciones hacia sus estados estacionarios localmente estables, y que éstos varían significativamente de un municipio a otro. Tercero, el patrón de convergencia local, que se produce a través de regiones contiguas, apunta no solo a la presencia de múltiples estados estacionarios y velocidades, sino que también sugiere la polarización de los patrones de crecimiento tipo catching-up, más allá de la visión tradicional de disparidades regionales Norte-Sur. Teóricamente la evidencia sostiene que, en México, más que un escenario de crecimiento desequilibrado entre los municipios, se registran múltiples equilibrios localmente estables.
La utilización de la regresión geográficamente ponderada permitió capturar los
patrones ya descritos. Así, el GWR funciona como un microscopio espacial (Fotheringham et al., 2002) de
las estimaciones globales; en consecuencia, el enfoque local es una herramienta útil
y tiene la ventaja de identificar patrones espaciales difícilmente percibidos por
las estimaciones globales. Pese a sus limitaciones, los estadísticos de contrastes
que han reforzado a este método, como las pruebas
Por otro lado, la posibilidad de realizar estudios con un enfoque local debe valorarse en función de la información disponible y de la riqueza y utilidad de los hallazgos. En relación con la información, los indicadores municipales de la actividad económica agregada están solo disponibles a través de los censos económicos (CE) de Inegi. Por ello, se utilizó, como variable proxi del nivel de actividad, el valor agregado censal bruto (VACB) que, al igual del PIB, es un indicador resumen que permite saber cuánto valor es agregado por un municipio y, en consecuencia, éste puede utilizarse como un indicador del nivel de producción o ingreso. No obstante, dadas las diferencias metodológicas de cobertura y valoración de la producción, los hallazgos aquí presentados deben leerse con las reservas del caso. Es decir, la hipótesis de convergencia local se pone a prueba a partir de la prevalencia de actividades industriales, comerciales y de servicios, de establecimiento fijo y en el sector formal de la economía.
Si bien el registro del VACB tiene el inconveniente de excluir a las actividades agropecuarias, vitales para los municipios rurales, así como la actividad informal que en los municipios urbanos tiene un peso importante, este indicador continúa siendo un reflejo del esfuerzo de los agentes económicos por emprender actividades de largo aliento. Pese a lo anterior, este es un indicador de la contribución económica municipal, información que aún no es posible conocer con la rigurosidad metodológica del Sistema de Cuentas Nacionales de México (SCNM). En cambio, el VACB posee una ventaja importante para los estudios espaciales, ya que los datos recabados corresponden al lugar geográfico donde se localiza la unidad económica y, por tanto, se realiza la producción.
En cuanto a la riqueza y utilidad de los hallazgos, resulta conveniente señalar que la convergencia, más allá de su planteamiento teórico, es una cuestión empírica que permite reflexionar sobre, entre otras cosas, la polarización, la distribución y la desigualdad. No obstante, los estudios se han centrado en la precisión de los métodos y la robustez de la inferencia de las estimaciones que ponen a prueba la convergencia. Pero, debe tenerse en cuenta que, más allá de la estimación puntual del nivel de ingreso de equilibrio, el enfoque local permite una panorámica de la reducción de las desigualdades económicas a escala municipal.
Atendiendo las disparidades, un proceso de convergencia local implica que la brecha en el nivel de ingreso entre economías pobres y ricas tenderá a disminuir, con el tiempo, hasta el punto en el cual las economías contiguas registren un mismo nivel de ingreso para una microrregión. Esta lectura, a partir de la Primera Ley de la Geografía, permite observar este proceso de manera más realista al capturar la no-estacionariedad: se observa un patrón geográfico en el cual la velocidad de convergencia aumenta de Norte (municipios más ricos) a Sur (municipios más pobres), en donde se registra la disminución de las brechas de ingreso, pero en un contexto local; y en el cual el proceso de apalancamiento (catching-up) se observa en varias intensidades, en varias direcciones y a partir de distintos núcleos o enclaves.
En virtud de lo anterior, el diseño e implementación de la política pública requiere de un enfoque microrregional, pues existe evidencia de que las brechas municipales de ingreso disminuyen, pero en el ámbito local. Si la convergencia ocurre en un contexto de ausencia de políticas regionales y restricciones presupuestales de los gobiernos municipales, entonces, el proceso se explica por la dinámica económica y espacial inherente, más que por una estrategia deliberada de promoción económica. Por otro lado, una política regional deliberada podría reducir más rápidamente las brechas en el desarrollo municipal; de ahí que, desde el punto de vista de la política pública, la investigación de las dinámicas de las disparidades regionales puede ser vista como una herramienta de evaluación de la efectividad de la política regional.
Futuras líneas de investigación requieren, en primer lugar, reflexionar teórica y conceptual sobre las implicaciones de la no-estacionariedad espacial en la dinámica económica municipal y en la reducción de las disparidades microrregionales, de tal manera que pueda esclarecerse no solo su naturaleza, sino también el origen de tal heterogeneidad, incluso a nivel sectorial de actividad económica. En segundo lugar y ante la pertinencia de un enfoque de regímenes espaciales, se requiere de un abordaje microrregional que supere la regionalización político-administrativa. Finalmente resultará de gran utilidad, ante la necesidad de trabajar con modelos más refinados, que no enmascaren los patrones espaciales, el considerar un enfoque local en el análisis de las diferencias subyacentes de las dinámicas territoriales.











 nueva página del texto (beta)
nueva página del texto (beta)



