1.1. Apertura comercial

De acuerdo con el teorema Stolper-Samuelson (SS) (¹⁹⁴¹), el comercio afecta al precio relativo de los factores porque ocasiona cambios en el tipo de trabajo que se demanda. De manera clara, el teorema SS indica que si una economía en desarrollo (intensiva en trabajo poco calificado), incrementa su comercio con países desarrollados (intensivos en trabajo calificado), la economía en desarrollo se especializará en la exportación de bienes intensivos en trabajo poco calificado, ocasionado que la demanda y el salario de los trabajadores poco calificados incremente, y que el de los trabajadores calificados, disminuya.

Lo contrario se observará en la economía en desarrollo, esta se especializará en la exportación de bienes intensivos en trabajo calificado, ocasionando que la demanda de este tipo de trabajo aumente, lo mismo que su salario. Por tanto, economías en desarrollo como la mexicana, de mayor comercio con economías desarrolladas, ocasionaría un incremento en la demanda relativa del trabajo no calificado, que se traduce en un incremento en la remuneración al trabajo no calificado, y en un incremento en el salario relativo de este tipo de trabajo, que podría significar una reducción en la desigualdad salarial porque el salario de los trabajadores no calificados experimenta un incremento, como consecuencia del comercio (ver ^{Esquivel y Rodríguez, 2003} y ^{Hoekman y Winters, 2005}).

Además, si se considera que en los últimos 10 años, el 88.8% del comercio mexicano se realiza con países desarrollados como EE. UU., Canadá, Europa y Japón (^{Banxico, 2019}), que se caracterizan por ser países abundantes en trabajo calificado, entonces México debió experimentar una reducción en la desigualdad salarial como resultado del comercio.

De acuerdo con Chiquiar et al. (²⁰¹⁷), la integración de México con países desarrollados como EE. UU. y Canadá a través del TLCAN, ahora T-MEC, llevó a que el empleo manufacturero de trabajadores no calificados aumentara y a que sus salarios reales fueran mayores. Estos resultados coinciden con los que reportan Cañonero y Werner (²⁰⁰²) y Esquivel y Rodríguez (²⁰⁰³) quienes argumentan que con la inserción de México al GATT la desigualdad salarial se incrementó como resultado del aumento en la oferta de empleo no calificado, pero que se redujo después de la instrumentación del TLCAN porque aumentó el comercio con países abundantes en trabajo calificado. Estos hallazgos apoyan el cumplimiento del teorema SS en México.

Sin embargo, se ha encontrado que el comercio y las reformas al comercio explican solo una pequeña fracción del cambio en la desigualdad salarial, observado en países desarrollados y en desarrollo. De acuerdo con Hoekman y Winters (^{2005: 24}), “… las magnitudes de los efectos de mayor comercio en países de la OECD sobre los salarios y la desigualdad son pequeñas.”

Por otro lado, en el trabajo de Chiquiar et al. (²⁰¹⁷), hay evidencia que sugiere que el comercio tiene efectos diferenciados en las regiones de México; y, que las ciudades del norte, al tener mayor exposición al TLCAN, han experimentado mayor crecimiento en los salarios. Además, Akerman, et al. (²⁰¹³), argumentan que la apertura comercial puede incrementar la desigualdad salarial al interior de la industria manufacturera y de los subsectores, ya que no todas las empresas exportan y no todas se benefician del consecuente incremento salarial. Harrison y Hanson (¹⁹⁹⁹) refieren que al interior de las industrias, la desigualdad salarial es mayor cuanto mayor es su presencia en actividades de exportación.

1.2. Cambio técnico

El cambio técnico se define como el cambio en la estructura y contenido de la producción, e implica un mejoramiento o un cambio en las dinámicas de producción existentes, en el conjunto de factores que se combinan, o en las cantidades que se utilizan. Murillo-Villanueva (²⁰¹⁹) da evidencia de que entre 2003 y 2012 el cambio técnico en los subsectores manufactureros de México fue gradual, y con cambios importantes en la intensidad con la que se utilizan los insumos primarios. Particularmente, se observa que la mayoría de los subsectores experimentan una reducción en el empleo, que sugiere una relación sustitutiva entre capital y trabajo de baja calificación, y una relación de complementariedad entre capital y trabajo calificado.

El cambio técnico ocasiona variaciones en la composición del empleo a favor del trabajo calificado e incrementa la desigualdad salarial. De acuerdo con Broecke (²⁰¹⁶), la globalización, los cambios en la demanda de capacidades y los cambios organizacionales han incrementado el pago a las capacidades y, por tanto, la desigualdad salarial.

Esquivel y Rodríguez (²⁰⁰³) encuentran que en la industria manufacturera el cambio técnico llevó a una reducción en los salarios reales de los trabajadores no calificados, y a un incremento en el salario real de los calificados, presionando a la alza la desigualdad entre calificados y no calificados entre 1988 y 2000. Al respecto, hay diversos trabajos que indican que la calificación del trabajo influye sobre los salarios, y que los trabajadores con mayor calificación tienen en promedio mayores salarios que los no calificados (^{Krugman y Lawrence, 1993}; ^{Hoekman y Winters, 2005} y ^{Cañonero y Werner, 2002}).

En algunos de estos trabajos se ha utilizado a la variable productividad laboral como proxy del cambio técnico. La idea detrás de este supuesto es que el cambio técnico incrementa la productividad laboral, vía la reducción en el uso de trabajo. Castellano (²⁰¹⁰) presenta evidencia de que, en la industria manufacturera, el incremento de la productividad laboral se traduce en un incremento en los salarios. Los diferenciales entre las productividades laborales entre subsectores podrían llevar a distintos niveles de salario, y a agravar la desigualdad salarial.

También se considera que el perfil tecnológico de los subsectores manufactureros es un indicador de cambio técnico, que contribuye a la explicación de la desigualdad salarial en el sentido de que, a mayor innovación, la desigualdad se agudiza. Se utiliza la clasificación de la Organización para la Cooperación y el Desarrollo (OCDE), basada en indicadores de intensidad tecnológica que reportan Carbajal-Suárez, Mejía-Reyes y Rendón (²⁰⁰⁸) y que clasifica a los subsectores de la manufactura en cuatro categorías: alta tecnología, tecnología alta-media, tecnología baja-media y tecnología baja.

1.3. Cambios en el mercado laboral

La fragmentación de los procesos productivos de las grandes empresas y la creciente relevancia de las cadenas globales de valor han tenido como principal objetivo la búsqueda de bajos costos laborales y el incremento en la tasa de ganancia. Por ello se han desarrollado nuevas formas de organización del trabajo que, de acuerdo con Hernández (^{2012: 34}), “no siempre resultan benéficas para los trabajadores”.

La nueva organización del trabajo es resultado de las reformas laborales que fomentan la flexibilidad laboral y la reducción de la participación sindical como vías para incentivar el empleo. En la actualidad, se observan contrataciones sin seguridad laboral y con remuneración flexible determinada por la duración de la jornada laboral, el rendimiento, la productividad del trabajo o los beneficios de la empresa (ver ^{Neffa, 2010}). Hernández (²⁰¹²) refiere que, en 2011, el 56.88% de los trabajadores mexicanos tuvieron empleos temporales, sin contrato formal o con contratos que no especificaban la duración. En ese sentido, la reforma laboral de 2012 que tuvo por objetivo fomentar el acceso al mercado laboral a través de la flexibilidad laboral, podría traducirse en un incremento en la desigualdad salarial.

Aunado a esto, la reducción de la participación sindical también afecta a la desigualdad salarial, especialmente, reduce las remuneraciones de los trabajadores menos calificados. No obstante, de acuerdo con Cragg y Epelbaum (¹⁹⁹⁶), Bell (¹⁹⁹⁷) y López-Acevedo (²⁰⁰¹), hasta finales del S. XX, en México, la pérdida de poder sindical no afectó la evolución de la desigualdad salarial.

1.4. Cambios en la oferta de empleo

Respecto a la oferta de empleo, se ha encontrado evidencia que sugiere que la participación femenina y juvenil, así como el desempleo, son variables que afectan la oferta relativa de empleo y que inciden sobre la desigualdad salarial. Topel (¹⁹⁹⁴) sugiere que la oferta laboral femenina afecta el salario de los hombres menos calificados. En el mismo sentido, De la Garza et al. (²⁰⁰¹), encuentran que en México las mujeres se emplean en actividades de baja productividad ocasionando que la brecha salarial sea más amplia.

Contrario a la idea de que la liberalización comercial ha intensificado la desigualdad salarial entre hombres y mujeres, Aguayo-Tellez, Airola y Juhn (²⁰¹⁰) dan evidencia de que la liberalización comercial en México, aumentó la participación de las mujeres en el mercado laboral manteniendo estable la relación salarial entre hombres y mujeres.

Por otro lado, Meza (²⁰⁰⁵) encuentra que la participación de los jóvenes aumenta la desigualdad salarial al incrementar la oferta de empleo y abaratar los salarios. La presión que en México ejercen los jóvenes sobre la desigualdad salarial también podría ser relevante, si se considera que cada año se incorporan al mercado laboral más de un millón de jóvenes (ver ^{Hernández-Laos, 2000}).

Además, de acuerdo con los resultados que reporta Castellano (²⁰¹⁰) para México, en el corto plazo, un incremento de 1% en la tasa de desempleo de la industria manufacturera, reduce el incremento del salario nominal del sector en 0.54%. Lo anterior sugiere que el incremento en la oferta laboral detiene el crecimiento de los salarios y como consecuencia, incrementa la desigualdad salarial.

3.1. Desigualdad salarial

En este trabajo, la desigualdad salarial se refiere a la desigualdad en la distribución de los salarios entre obreros que se emplean en el mismo subsector, pero en distintas ramas. Para su medición, se utilizaron los datos de salarios reales por hora en cada una de las 86 ramas manufactureras que conforman los 21 subsectores y que reporta la Encuesta Mensual de la Industria Manufacturera (^{EMIM, 2019}), para el periodo 2007-2018; algunos subsectores se desagregan en 9 ramas, mientras que otros solo en 2. A partir de esta información, se calculó la desigualdad salarial al interior de los subsectores y entre ramas.

Para la obtención de medidas representativas de la desigualdad, se han utilizado distintos índices derivados de la curva de Lorenz (¹⁹⁰⁵) como el coeficiente de Gini (¹⁹¹⁴), el índice de Theil (1 y 2), el índice de diferencia absoluta media (AGC); también se han utilizado distintos indicadores de dispersión como los índices de entropía generalizada (ver ^{Atkinson y Bourguignon, 2000}, ^{Cowell, 2000} y ^{Heshmati, 2004}).

Aun cuando en la literatura se han encontrado diversas medidas de desigualdad, en este trabajo se utiliza el índice de Gini (¹⁹¹⁴). Este coeficiente es un instrumento para medir la concentración de ingresos entre la población de un país o región en un periodo determinado; se obtiene del área entre la curva de perfecta igualdad y la curva de Lorenz dividida por el área debajo de la línea de perfecta igualdad, se calcula a partir de la ecuación (1).

Donde q representa la proporción acumulada del producto entre salario unitario y horas trabajadas, p la proporción acumulada de horas trabajadas por los obreros en las i ramas manufactureras. Recuérdese que el índice de Gini toma valores entre 0 y 1, donde 0 representa un escenario de perfecta igualdad en la distribución de los salarios (todos tienen el mismo salario), y 1 representa la perfecta desigualdad salarial (una proporción de los trabajadores acapara todos los salarios).

Las ventajas de uso residen en que permite comparar las distribuciones de ingresos entre los subsectores manufactureros, es de fácil interpretación, se puede usar para indicar cómo ha cambiado la distribución del ingreso en los subsectores en el tiempo, además de que satisface las propiedades deseables que deben cumplir las medidas de desigualdad: invariancia a la escala, invariancia a las réplicas, simetría y el principio de transferencias, (o condición de Dalton-Pigou) (véase ^{Atuesta, Mancero y Tromben, 2018}). Este último establece que las transferencias de ingresos de trabajadores con altos salarios, a los de bajos salarios resultan en una distribución más equitativa.

Como se observa más adelante, el indicador de brecha salarial BSit también arroja resultados significativos en el análisis de los determinantes de la desigualdad salarial en los subsectores manufactureros. Este indicador se construyó para cada subsector, a partir de la diferencia salarial entre la rama manufacturera con el salario más alto y la rama con el salario más bajo.

3.2. Determinantes de la desigualdad salarial

Una vez obtenido el indicador de la desigualdad salarial, se plantea un modelo con datos de panel para la industria manufacturera que busca probar la significancia estadística de algunas de las variables revisadas en el primer apartado, como determinantes de la desigualdad salarial.

Para el caso que nos ocupa, se utilizan las variables siguientes para explicar la desigualdad salarial medida a través del coeficiente de Gini (Git) y de la brecha salarial (BSit) : el volumen de comercio exterior del subsector i en el periodo t (Cit) , que se define como la suma de las exportaciones e importaciones y que mide la intensidad de la apertura comercial; el índice de productividad laboral relativa¹ del subsector i en el periodo t (Pit) , el índice de subcontratación² del subsector i en el periodo t (Sit) , el total de obreros que se emplean en el subsector i y periodo t (Lit) , y el perfil tecnológico del subsector i en el periodo t (PTit). En el anexo 1, se presentan las estadísticas básicas de estas variables.

Por la evidencia de trabajos previos, que consideran a la calificación laboral como un factor central de la desigualdad salarial, quizá sea discutible que en este trabajo se considere la desigualdad entre obreros. Sin embargo, el interés por considerar este tipo de trabajadores se debe a que parte importante de la estructura del empleo, en el sector manufacturero, se compone de obreros; cifra que entre 2007 y 2018 ascendió a 80%. En este caso, el volumen de comercio se utiliza como un indicador absoluto de apertura comercial, el índice de productividad laboral y el perfil tecnológico como variables proxy del cambio técnico, y el índice de subcontratación como variable de flexibilidad laboral.

El indicador de flexibilidad laboral trata de incorporar los efectos que ha tenido la reforma laboral en México, a partir de su instrumentación formal en 2012, y de que entre los principales cambios a la Ley Federal del Trabajo, se plantea la regulación del outsourcing, contratos temporales a prueba y pagos por jornada laboral reducida, bajo el supuesto que estos mecanismos tendrían la capacidad de insertar a jóvenes y mujeres al mercado laboral (véase ^{Loría, Ramírez y Salas, 2015}).

Con relación al tema, Loría, Ramírez y Salas (²⁰¹⁵) proponen, para la realidad del mercado de trabajo en México, utilizar un indicador de flexibilidad laboral factual, que comprenda la tasa porcentual de trabajadores eventuales al total de trabajadores en el sector formal, siendo este un indicador de flexibilidad laboral numérica que representa la facilidad de contratación y despido en el mercado formal de trabajo en México. De ahí que el índice de subcontratación, en este trabajo, se considera como un indicador de flexibilidad laboral y por último, al nivel de empleo como variable de cambios en el mercado laboral.

Los datos de comercio total por subsector se obtuvieron del BIE (^{INEGI, 2019}), mientras que los índices de productividad laboral y subcontratación se construyeron con información de la Encuesta Mensual de la Industria Manufacturera (^{EMIM, 2019}). El modelo de datos de panel se estimó a partir de la ecuación (2).

Donde: i se refiere a la unidad de estudio de corte transversal (subsectores manufactureros) y t a la dimensión en el tiempo (datos anuales), la muestra total del modelo sería N = nxT, donde n corresponde a 21, que son los subsectores de la manufactura y T es igual a 12, que son los años que corresponden al periodo 2007-2018. Se tiene un panel balanceado con N igual a 252 observaciones. Los parámetros α, α1, α2, α3,α4 y α5 son los que estima el modelo, y el término uit hace referencia a los errores del modelo. En un modelo con datos de panel, el efecto de un cambio en las variables explicativas es el mismo para las i unidades de estudio en los t periodos, y la heterogeneidad se considera en el término de error uit (^{Wooldridge, 2002}). Esta última puede variar entre unidades de estudio i o entre unidades i y tiempo t (^{Hsiao, 2003}). En ese sentido, el término de error uit se compone de un efecto individual (mi) y de un término puramente aleatorio (eit) , de manera que la ecuación (2) se puede reescribir de la siguiente forma.

El componente de efecto individual puede tomar distintos valores según la heterogeneidad entre unidades de estudio. Si mi=0, se dice que no existe heteogéneidad no observable entre individuos, por lo que, tanto la ordenada al origen como las variables explicativas tienen el mismo efecto sobre todos los subsectores. En este caso, la ecuación del modelo sería como en la ecuación (3a) y representa un modelo de regresión agrupada o pooled.

Si mi≠0 , distinto para cada unidad de estudio i y constante a lo largo de T, se concluye que las variables explicativas tienen el mismo efecto sobre todas las unidades, pero que la ordenada al origen α es diferente para cada unidad y viene dado por mi . Este modelo se representa con la ecuación (3b) y se conoce como modelo de efectos fijos.

Por último, si mi≠0 y toma valores distintos para cada unidad y a lo largo del periodo, se dice que mi es una variable aleatoria. En este caso, los efectos individuales se distribuyen aleatoriamente alrededor de cierto valor; este modelo incorpora la heterogeneidad no observable en el término de error y no en la constante. A este tipo de modelos se le conoce como de efectos aleatorios y se representa con la ecuación (3), donde mi+eit=uit .

4.1. Desigualdad salarial entre los subsectores manufactureros

En un primer ejercicio, se estimó el coeficiente de Gini para medir la desigualdad salarial entre los subsectores de la industria manufacturera (ver gráfica 1). La gráfica 1 indica que la desigualdad salarial en la industria manufacturera es relativamente baja, oscila entre 0.13 y 0.17, se incrementó en la primera mitad del periodo como consecuencia de la Gran Recesión, pero comenzó a reducirse a partir del 2012. La reducción en la desigualdad salarial, en la segunda mitad del periodo, se explica por el efecto transitorio de la Gran Recesión en los salarios y, por una fuerte caída en el salario real de los subsectores de mayor salario, acompañado de un ligero incremento en el salario real de los subsectores con menor salario (ver tabla 1).

Los resultados se presentan en dos grupos. Por un lado, los subsectores de menor desigualdad salarial y, por otro lado, los de mayor desigualdad. Del total de 21 subsectores, 15 se encuentran en la primera categoría (ver tabla 2), y 6 en la segunda (ver gráfica 2).

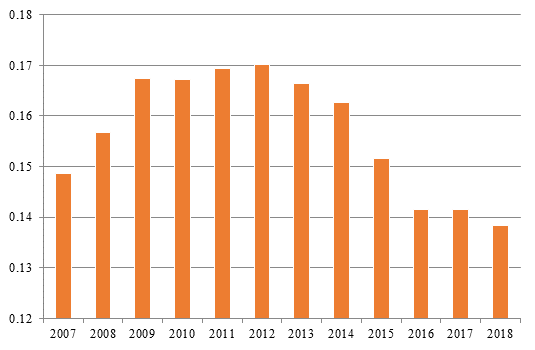
Fuente: estimaciones realizadas con datos de la EMIM (^{INEGI, 2019}).

Gráfica 1 Desigualdad salarial entre subsectores de la industria manufacturera, 2007-2018 

Ampliando el nivel de desagregación de las actividades manufactureras, se estimó la desigualdad salarial al interior de los subsectores manufactureros, es decir, entre las ramas de cada subsector.

En la tabla 2, se muestran los subsectores del primer grupo. Los resultados muestran que la desigualdad salarial en estos subsectores es muy baja, en la mayoría de los casos y años, el índice no rebasa la cifra de 0.1; además, la mayoría de estos subsectores se caracteriza por registrar los niveles más bajos de salario real por hora. Esto indica que la desigualdad salarial de los subsectores de textil y de calzado (313, 314, 315 y 316), de la industria de la madera (321), del papel (322), plástico (326), minerales no metálicos (327), productos metálicos (332), maquinaria y equipo (333), computación y comunicación (334), aparatos eléctricos (335), muebles (335) y otras manufacturas (339) es baja, porque los trabajadores reciben salarios que son bajos y que son muy similares entre ramas.

En la gráfica 2, se muestran los resultados del índice de Gini para los subsectores con mayor desigualdad salarial entre 2007 y 2018. En la mayoría de los subsectores, y a lo largo de este periodo, el índice de Gini oscila entre 0.1 y 0.3.

Vemos que el subsector con la desigualdad salarial más elevada es el de fabricación de derivados del petróleo. Esto indicaría que, en términos de salarios, no es lo mismo trabajar en la rama de refinación de petróleo (324110), que en la de fabricación de productos de asfalto (324120) o en la de fabricación de aceites y grasas (324191); los salarios difieren de manera importante entre las tres ramas del mismo subsector.

La industria química (325) es otro subsector donde la desigualdad salarial es elevada, aunque en los últimos años, ha reducido de manera importante (ver gráfica 2). En los subsectores de la industria alimentaria y de metálicas básicas la desigualdad salarial se ha mantenido relativamente constante. Por el contrario, en la industria de bebidas y tabaco, la desigualdad se ha incrementado.

La evidencia de que en la mayoría de los subsectores la desigualdad salarial entre ramas de un mismo subsector se ha reducido, explica porqué el índice de Gini total manufacturero se ha reducido en los últimos años.

Fuente: estimaciones propias con datos de la EMIM (²⁰¹⁹).

Gráfica 2 Desigualdad salarial en los subsectores manufactureros con el mayor índice de Gini, 2007-2018 

4.2. Determinantes de la desigualdad en los subsectores manufactureros

A partir de los índices de desigualdad salarial de los 21 subsectores manufactureros, se integró un panel de datos balanceado de 252 observaciones, resultado de 21 unidades transversales, una para cada subsector y 12 unidades temporales que corresponden al periodo 2007-2018. Se estimó la desigualdad salarial de los subsectores de la manufactura a partir de la especificación de las ecuaciones (3a) y (3b), de la siguiente forma:

donde:

ln⁡Git = coeficiente de Gini (en logaritmos) de la manufactura, del subsector 1 al 21.

ln⁡Cit = el volumen de comercio exterior de la manufactura, del subsector 1 al 21 (en logaritmos).

Pit = índice de productividad laboral de la manufactura, del subsector 1 al 21.

Sit = índice de subcontratación de la manufactura, del subsector 1 al 21.

ln⁡Lit = población ocupada en la manufactura, del subsector 1 al 21 (en logaritmos).

PTit = perfil tecnológico, del subsector 1 al 21.

Con el propósito de aportar mayor evidencia de los determinantes de la desigualdad salarial, se estimó la ecuación (4), considerando a la brecha salarial como variable dependiente.

Se estimaron modelos de datos agrupados, de efectos fijos y de efectos aleatorios y se aplicaron las pruebas de datos agrupados (pool test) y la de Hausman, que contrasta las estimaciones de efectos fijos y efectos aleatorios. Si se encuentran diferencias significativas, se rechaza la hipótesis nula de igualdad debido a que seguiría existiendo correlación entre el término de error y los regresores; en tal caso, se opta por el modelo de efectos fijos. Si, por el contrario, las estimaciones son significativamente iguales, se elige el modelo de efectos aleatorios. Se concluyó que el modelo de datos agrupados es consistente con efectos fijos, por lo que no fue necesario estimar los modelos con efectos aleatorios. Los resultados de las pruebas arrojaron valores del estadístico F con probabilidades mayores a 0.05 (ver tabla 3).

A partir de la evidencia empírica y la revisión de literatura que se presentó en el apartado 1, se esperaba encontrar las siguientes relaciones entre las variables elegidas, como determinantes de la desigualdad salarial: a) el incremento en el volumen de comercio ( ln⁡Cit ) ha incrementado la desigualdad salarial en los subsectores, a causa de la marcada heterogeneidad en términos de su vinculación con el sector externo; b) mayor productividad laboral ( Pit ) sugiere cambio técnico, que lleva a un incremento en la desigualdad salarial vía una reducción en los salarios de los trabajadores no calificados, y un incremento en los de los calificados; c) a mayor subcontratación laboral ( Sit ), medida de la flexibilidad laboral, mayor desigualdad salarial; d) una relación positiva con el crecimiento del empleo ( ln⁡Lit ); e) una relación positiva con el perfil tecnológico ( PTit ), en el sentido de que a mayor perfil tecnológico, se agudiza la desigualdad salarial en los sectores de actividad.

Al estimar la función de desigualdad salarial a partir del índice de Gini, como se expresa en la ecuación 4, destacan los resultados siguientes: el crecimiento de la productividad del trabajo ( Pit ), de la subcontratación laboral ( Sit ) y del empleo ( Lit ) aportan evidencia para considerar que son elementos que contribuyen al incremento de la desigualdad salarial en la manufactura.

Por la magnitud de los coeficientes Sit (0.092), ln⁡Lit (0.027) y Pit (0.019), los resultados indican que las condiciones que prevalecen para la contratación del factor trabajo, en los subsectores de la manufactura asociados a la flexibilidad laboral, han sido una de las principales causas para explicar la desigualdad salarial en los subsectores de la manufactura (ver tabla 3), evidencia que coincide con los trabajos de Neffa (²⁰¹⁰) y Hernández (²⁰¹²). Por su parte, se probó que el aumento en la oferta laboral, conduce a un aumento en la desigualdad salarial tal y como lo sugiere Castellano (²⁰¹⁰). Y que el incremento de la productividad laboral (variable proxy del cambio técnico y de la calificación laboral), influye de manera directa en el crecimiento de la desigualdad salarial, como lo recomienda la revisión teórica del apartado 1 (ver ^{Cañonero y Wernes, 2002}; ^{Esquivel y Rodríguez, 2003} y ^{Hoekman y Winters, 2005}).

Si bien se ha argumentado que el proceso de apertura comercial favorecería el crecimiento de la economía por las bondades del tamaño de mercado, y entre los beneficios se observaría un mejoramiento en los niveles salariales de los trabajadores mexicanos, la evidencia indica que el coeficiente de ln⁡Cit (-0.001), variable proxy de la apertura comercial, no es significativa; aunque el signo sugiere que puede ser una condición para disminuir la brecha salarial en los subsectores de la manufactura, como lo indica la revisión teórica. En relación con el perfil tecnológico PTit que prevalece en los subsectores de la manufactura, el coeficiente estimado no es significativo, sin embargo, por el signo también dejaría ver la posibilidad de que pueda explicar la desigualdad salarial que prevalece en la manufactura.

A partir de estos resultados, se buscó evidencia adicional, por lo que se construyeron indicadores de desigualdad salarial adicionales al índice de Gini. Específicamente un índice de entropía generalizada, un índice de desigualdad intersectorial y el indicador de brecha salarial ( BSit ). Al trabajar con el índice de Theil y con el índice de desigualdad intersectorial no se encontraron resultados consistentes, pero sí con el indicador de brecha salarial ( BSit ).

Como se reporta en la tercera columna de la tabla 3, aunque en magnitudes diferentes, los resultados del modelo que utiliza a BSit como variable dependiente, son consistentes con los que utilizan Git , en el sentido de que los coeficientes Sit , ln⁡Lit y Pit continúan siendo significativos. Se debe puntualizar que lo importante de estos resultados es que se confirma que un factor central en la explicación de la desigualdad salarial, en los subsectores de la manufactura, es el índice de subcontratación Sit (coeficiente de 39.8), que muestra un mayor coeficiente respecto a las demás variables consideradas (ver resultados de estimación con la brecha salarial en la tabla 3). Este hecho deja ver que la política de flexibilidad laboral del mercado de trabajo ha generado efectos adversos en la desigualdad salarial del sector.

Del segundo modelo, también se observa que las variables de comercio exterior ln⁡Cit y perfil tecnológico PTit influyen de manera significativa a la desigualdad salarial del sector. Por un lado, se prueba la relación inversa entre la apertura comercial y la desigualdad, mayores niveles de comercio exterior ( ln⁡Cit ) reducen la brecha salarial porque el salario de los trabajadores no calificados incrementa, mientras que el de los calificados se reduce (ver ^{Stolper-Samuelson, 1941}) y, por otro lado, el perfil tecnológico PTit , variable proxy del cambio técnico contribuye al incremento de la brecha salarial.