INTRODUCCIÓN
Los modelos markovianos de cambio de régimen1 son modelos de análisis en los que se permite caracterizar una serie de tiempo x= [xt] en dos o más regímenes de comportamiento o estados de la naturaleza. Esto supone que la serie de tiempo no está modelada por medio de un único proceso estocástico xt~P (xt,θ) , que genera las realizaciones o valores de la misma, sino en s = 1,2, … , S procesos estocásticos diferentes. Procesos estocásticos que se combinan para formar uno solo por medio de una función de verosimilitud combinada y multimodal, dado un vector de parámetros θ:
En la expresión anterior, ωs=i es la ley de combinación que determina la proporción de datos que pertenecen al régimen s = i y P (xt, θ) su correspondiente sub-función de probabilidad. Para el caso específico que interesa en el presente trabajo, no se supone que el proceso estocástico que genera las realizaciones de una serie de tiempo corresponde a una función de probabilidad gaussiana unimodal con un solo parámetro de localización (µ) y uno de escala (µ), sino a (σ) parámetros, correspondientes a cada régimen o estado de la naturaleza (µs=i, σs=i).
Partiendo de la forma general de función de probabilidad multimodal dada en (1), conduce a que las realizaciones u observaciones de una serie de tiempo sean catalogadas o caracterizadas en sub-conjuntos o sub-muestras con sus propias sub-funciones de probabilidad y parámetros. Estas mismas llevan a la función general de probabilidad, inherente al proceso estocástico de la serie de tiempo x:
La función dada en (2) corresponde a la de una “mixtura gaussiana” porque ωs=1
representa la proporción o peso que los datos del régimen tienen en la muestra y en
la función general de probabilidad (2). Sin embargo, el modelo de mixtura gaussiana
presupone que la pertenencia a una de las subfunciones P
(xt, θs=i ) es fija a lo largo de t y, de
esta forma, “estática” para todos los datos de la serie de tiempo. Por esta razón,
no se pueden hacer inferencias, tales como: la probabilidad de que la o el
observador en t se encuentre en un periodo caracterizado por el
régimen s = 1 y su correspondiente sub-función de probabilidad
P (xt, θ) , así como la
probabilidad
Con esto, (2) puede ser reexpresado, no como fijo a lo largo del tiempo, sino como una función de probabilidad cambiante para cada estado P (xt, θ) a lo largo del tiempo. Dado esto, se generan, como parámetros de salida adicionales, las citadas probabilidades “suavizadas” P (xt, θ) =
A partir de ello, (2) se puede filtrar y suavizar a lo largo del tiempo, generando un vector
de parámetros de salida más amplio con las probabilidades suavizadas
Con el citado vector de parámetros, la función de verosimilidad del filtro de Hamilton puede expresarse, dado (2) , como sigue:
Dado esto, son de interés en materia financiera los parámetros
Con base en esta breve introducción a la lógica de los modelos markovianos de cambio de régimen, así como su aplicación práctica en materia financiera, se plantea el objetivo del presente trabajo: utilizar el filtro de Hamilton dado en (5) para determinar, en primera instancia, si el mismo es adecuado para modelar la serie de tiempo de los índices accionarios de mercados financieros pertenecientes a países considerados economías emergentes por la compañía Standard & Poors Indexes. Después del citado objetivo, se establece caracterizar el comportamiento estadístico y la eficiencia media-varianza2 de cada caso para llegar a las correspondientes conclusiones y beneficio del empleo del citado filtro en la práctica profesional financiera.
En el siguiente apartado se hace una breve revisión de los trabajos que, en materia financiera, aplican (5), para seguir con el correspondiente análisis de datos y resultados, así como las conclusiones y guías para futuros trabajos de investigación.
REVISIÓN DE TRABAJOS DE REFERENCIA
Dentro de los trabajos que emplean el filtro de Hamilton
(1989, 1990) para caracterizar el
comportamiento de series de tiempo económicas y financieras se cita el caso del
propio Hamilton (1989, 1990, 1994), quien
emplea su propuesta para modelar la probabilidad de que la economía de los Estados
Unidos se encuentre en un periodo de recesión (
En un estudio análogo para el caso latinoamericano, Mejía (2000) estudia el PIB per cápita de economías de países latinoamericanos como Argentina, Bolivia, Brasil, Chile, Colombia, México, Perú y Venezuela. En los resultados se encuentra evidencia a favor del empleo de modelos de dos regímenes, así como elementos para corroborar lo establecido en trabajos previos (Bollerslev et al., 1988; Engle, Ng & Rotschild, 1990; Ang & Chen, 2002; Hass, Mitnik & Paolella, 2009; Engle, Ghysels & Sohn, 2013). Trabajos que demostraron que el comportamiento de los rendimientos en periodos o regímenes de alta volatilidad son asimétricos. Es decir, en un periodo de recesión o “crisis”4 los rendimientos5 negativos tienden a ser proporcionalmente mayores que los rendimientos positivos en el citado periodo de crisis, así como mayores en magnitud que los rendimientos negativos de periodos considerados “normales”. De manera complementaria, Mejía (2000) encuentra evidencia en contra de la existencia de un ciclo macroeconómico latinoamericano y encuentra cierta concordancia en el comportamiento de los periodos de crisis para las duplas Estados Unidos- Chile, Brasil-Perú.
Canarella y Pollard (2007), estudiaron el desempeño de los índices bursátiles latinoamericanos correspondientes a Argentina, Chile, México Perú y Venezuela con modelos de interés similar al presente trabajo. Sus resultados observan que el filtro de Hamilton (1989), aplicado en periodicidades mensuales, es adecuado para determinar los periodos de crisis financiera, siendo estos coincidentes con crisis de tipo financiero o político en los países estudiados.
Adicionalmente, observan que los periodos de alta volatilidad o s = 2 son relativamente breves en duración (de 2 a 4 meses). Además, Mejía (2000) realiza un estudio similar al de Hamilton (1994), modelando el PIB per-cápita de Argentina, Bolivia, Brasil, Chile, Colombia, México, Perú, Estados Unidos y Venezuela con un filtro de Hamilton de dos regímenes. Sus pruebas llevan a observar que no existe un ciclo de expansión y contracción latinoamericano y que solo algunas duplas de países son las que tienen un nivel de concordancia: Brasil-Perú y Estados Unidos-Chile (Mejía (2000).
Cabrera y otros (2017)), en línea a la perspectiva de análisis de Mejía (2000) emplean el filtro de Hamilton (1989) en los índices bursátiles de países latinoamericanos como Argentina, Bolivia, Brasil, Colombia, México, Estados Unidos y Perú. Sus conclusiones llevan a observar que un modelo de 3 regímenes es adecuado para modelar estos mercados y que tampoco existe un ciclo latinoamericano de expansión y contracción en estos mercados que sea marcadamente claro. Solo resaltan un nivel de concordancia entre Estados Unidos, México y Chile.
Valera y Lee (2016) realizan pruebas de raíz unitaria a los índices de los países asiáticos, tales como: China, Filipinas, Hong Kong, Indonesia, Malasia y Singapur. Sus conclusiones llevan a observar que la hipótesis nula de cointegración, empleando la prueba Dickey-Fuller (1979), se sostiene para series de tiempo mensuales de enero de 1995 a junio de 2015.
Anterior a este trabajo y de forma análoga para modelar el comportamiento del tipo de cambio contra el dólar de las monedas de China, Corea del Sur, Hong Kong, Japón, Singapur y Taiwán, se tiene el trabajo de Wu (2015).
Wu (2015) emplea el filtro de Hamilton y su versión con matrices de probabilidades de transición cambiantes a lo largo del tiempo en las citadas divisas. El modelo empleado tiene, como regresoras el nivel de masa monetaria, la producción industrial, la tasa de interés de corto plazo y la de largo plazo. Los resultados que arroja sugieren que existen dos regímenes de volatilidad en las paridades estudiadas y que existe una fuerte relación entre los niveles de volatilidad de las paridades y los valores de variables como la producción industrial.
Para el caso de países emergentes africanos, se cita el trabajo de Balcilar y otros (2017), quienes estudian la influencia del precio del petróleo en el nivel de crecimiento real de la economía de Sudáfrica. Al emplear el filtro de Hamilton en un Vector Autorregresivo (VAR) con dos regímenes, encuentran que el precio de dicha mercancía es altamente influyente en el nivel de crecimiento económico sudafricano en la fase o régimen expansivo. Para el caso de medio oriente, se encuentra el trabajo de Balcilar, Demirer y Hammoudeh (2013), quienes analizan el caso de los mercados financieros del Golfo Arábigo: Arabia Saudita, Qatar, Dubai y Kuwait para el intervalo de tiempo de periodicidad diaria del 7 de septiembre de 2006 al 28 de septiembre de 2011.
Con sus pruebas encontraron que estos mercados se caracterizan por tres regímenes de volatilidad (baja, alta y extrema -o quiebra-) y resaltaron que existe un comportamiento de rebaño o nerviosismo colectivo entre Arabia Saudita, Dubai y Kuwait en el periodo de quiebra o extrema volatilidad y en el de alta volatilidad para el caso qatarí. También resaltan que, contrario a los mercados de países desarrollados, estos cuatro casos tienen transiciones que inician en el periodo de baja volatilidad para pasar al de extrema o quiebra, terminando con muy alta volatilidad (Balcilar, Demirer & Hammoudeh, 2013).
Como se aprecia, utilizar el filtro de Hamilton (1989) para modelar el comportamiento de series de tiempo propias de índices bursátiles no es una asignatura nueva; pero sí es de interés para fines de inversión. A pesar de este interés, no se tienen referencias o antecedentes de trabajos en donde se caracterice el comportamiento de los mercados de economías emergentes en su conjunto y por bloques, Latinoamérica, Asia, Europa del Este, Medio Oriente, Africa y los BRIC (Brasil, Rusia, India y China). Esto para comparar su caracterización de cada caso en lo particular contra el bloque de economías emergentes en su conjunto y contra el comportamiento del bloque norteamericano (Estados Unidos y Canadá); así como contra la caracterización del desempeño de un índice accionario mundial que incluye el desempeño de economías desarrolladas y emergentes.
Ante esta necesidad surge el objetivo del presente trabajo: caracterizar en un modelo de dos regímenes de volatilidad, el desempeño de los índices expuestos en la tabla 1. Como se aprecia en dicha tabla, se modela el desempeño de los mercados propios de economías (países) considerados desarrollados y emergentes por medio de los índices de capitalización bursátiles BMI calculados por la compañía Standard & Poors - Dow Jones Indices LLC. Esta última es una de las compañías calificadoras y de análisis financiero más reconocidas en el mundo. A su vez, es de las más aceptadas para fines de cálculo de índices de desempeño en la industria de administración de inversiones (portafolios), para calcular y publicar índices de desempeño de diferentes tipos de activos financieros, mercados, estilos de inversión y estrategias de portafolios institucionales. Por citar algunos ejemplos, el reconocido índice S&P500 de Estados Unidos, el IPC de la Bolsa Mexicana de Valores, el S&P BMI Global Equity Index y otros son de los índices más empleados para medir el desempeño de los respectivos mercados que se estudian.
Tabla 1 Relación de índices, suticker (código de identificación)
| NOMBRE DE INDICE | PAIS ESTUDIADO | TICKER | FECHA INICIAL | FECHA FINAL |
|---|---|---|---|---|
| S&P GLOBAL 100 | Global | GLOBAL | 26/12/2000 | 30/03/2018 |
| S&P 500 | EEUU | SP500 | 30/12/1994 | 30/03/2018 |
| S&P BMI EMERGING MARKETS INDEX | Países emergentes alrededor del mundo | EMERGING | 30/12/1994 | 30/03/2018 |
| S&P BMI LATIN AMERICA EMERGING MARKETS INDEX | Países de Latinoamérica | LATAM | 30/12/1994 | 30/03/2018 |
| S&P BMI ASIA/PACIFIC EMERGING MARKETS INDEX | Asia | ASIAPAC | 30/12/1994 | 30/03/2018 |
| S&P BMI EUROPEAN EMERGING MARKETS INDEX | Europa del Este: Rusia, región balcánica y del Bósforo | EMEURO | 30/12/1994 | 30/03/2018 |
| S&P BMI MIDDLE EAST & AFRICA | Medio oriente y África | MOAFRICA | 30/12/1994 | 30/03/2018 |
| S&P BMI BRIC INDEX | Brasil, Rusia, India y China | BRIC | 15/08/2006 | 30/03/2018 |
Fuente: S&P Dow Jones indices LLC (2018).
Para fines más específicos, se utilizan los índices de capitalización globales y regionales S&P Broad Market Index (BMI), cuya metodología de cálculo se describe en S&P Dow Jones índices LLC (2018).
Dicho esto, y antes de proceder, queda una cuestión por resolver ¿Qué se entiende por país emergente? En estricto sentido, es un término que se ha ido desarrollando a lo largo del tiempo. El Banco Mundial y el Fondo Monetario Internacional han buscado categorizar los países en términos de su crecimiento económico, estabilidad y desarrollo social, así como un término político y financiero. Incluso el término de “economía emergente” o “país emergente” es resultado de un proceso evolutivo sobre la clasificación de países de tercer, segundo y primer mundo que se utilizó en los periodos de la guerra fría.
Para fines de acotación y fines prácticos en la exposición, en la práctica profesional de las inversiones se emplea un criterio de clasificación de mercados financieros, partiendo de la liquidez, accesibilidad, flexibilidad y tamaño de los mercados financieros de un determinado país, así como de su estabilidad en el crecimiento y desarrollo social.
Este mismo, diferencia a los mercados con grado de inversión (conjunto de interés en el presente trabajo) de aquellos que no son aptos para dicha actividad por parte de inversionistas ajenos a la nación de estudio. Dentro de los países con grado de inversión se encuentran, según se establece en la metodología de clasificación de países de Standard & Poors (S&P Dow Jones Indices LLC, 2016), los niveles y criterios de clasificación expuestos en la Tabla 2. Con esta clasificación en mente, que permite definir “mercado de una economía emergente” o simplemente “mercado emergente” y para fines exclusivamente del presente trabajo, se procede a la descripción de los datos y su método de procesamiento para pasar a la revisión de resultados observados.
Tabla 2 Los criterios para clasificar a un mercado financiero como desarrollado, emergente o de frontera
| Tipo de Mercado | Requisitos para la clasificación |
|---|---|
| Mercado de economía desarrollada Mercado de Economía emergente | Los necesarios de cubrir por parte de un mercado emergente más un PIB per cápita mayor o igual a USD$15,000.00 en su país sede. |
| Los necesarios de cubrir para un mercado de frontera más los siguientes: | |
| Mercado frontera | |
Fuente: S&P Dow Jones Indices (2016).
ANÁLISIS DE SERIES DE TIEMPO CON EL FILTRO DE HAMILTON EN LOS ÍNDICES DE INTERÉS
Procesamiento de datos
El análisis o caracterización en dos regímenes o estados de la naturaleza se realiza para los índices descritos en la tabla 1, en los periodos de inicio y fin también mencionados en dicho cuadro con datos de periodicidad semanal extraídos de las bases de datos de Reuters.
A los niveles de índice Pt observados se les calculó el rendimiento pagado o logrado por el índice en cada semana con el método de la variación porcentual en tiempo continuo:
A los valores de Δ%Pt se les aplicó el filtro de Hamilton (1989), utilizando la función de verosimilitud dada en (5),
a fin de lograr los parámetros de media de cada régimen µs=i,
desviación estándar σs=i, probabilidades suavizadas de estar en
determinado régimen
Dentro de los parámetros de salida que se lograron, se utilizaron los vectores de probabilidades de transición y se caracterizó a cada uno como propio del régimen de crisis o alta volatilidad (s = 2) al vector de probabilidades de transición que cumple con la siguiente:
De los dos vectores de probabilidades suavizadas, logrados con el filtro de Hamilton, uno de ellos pertenece al régimen 2 si su correspondiente desviación estándar es la más alta en el vector de desviaciones estándar que entrega la aplicación de dicho filtro. Ejemplo, el filtro de Hamilton, al emplear (5) aplica a cada realización de la serie de tiempo cada una de las funciones de probabilidad gaussiana de cada régimen que genera un vector de T×S, según se sugiere en Hamilton (1989, 1994):
Cada columna en la tabla 1 tiene su correspondiente media y desviación estándar. Por lo general, si los datos no presentan irregularidades en su medición, o si la serie de tiempo que se estudia es de un fenómeno o variable que no es afectada por alguna distorsión (social, política o tecnológica) entonces el régimen que tiene la desviación estándar más pequeña (es decir, de un periodo “normal” o de baja volatilidad) corresponde a la columna de la izquierda. Sin embargo, como sucedió en el trabajo de Balcilar, Demirer y Hammoudeh (2013), esto puede cambiar dada la naturaleza de los mercados árabes de ser mercados de frontera, según los criterios establecidos en la tabla 1.
Esto los lleva, dada su baja liquidez de mercado y operatividad, a tener comportamientos más atípicos que los propios de una economía emergente o desarrollada. Debido a esto último, y a la aplicación del método de Quassi-máxima verosimilitud sugerido por Hamilton (1994), se puede tener el resultado de que en realidad el régimen sea el correspondiente al vector de probabilidades suavizadas de la derecha en (8), y no el de la izquierda como habitualmente se espera. Dado esto es que se aplica la regla dada en (7) para discernir qué vector de probabilidades corresponde a cada uno de los regímenes.
Cabe resaltar que lo propio se hace para determinar la media y la columna en la matriz de probabilidades de transición. Por ejemplo, si la columna izquierda en (8) corresponde al régimen s = 1, se entiende que la media, desviación estándar y primera columna de la matriz P de probabilidades de transición corresponden también a dicho régimen.
Una vez que se caracterizan los parámetros de salida en cada régimen, se utilizan los mismos
(en especial las probabilidades suavizadas de cada régimen
xt∈s=2⇔
Las realizaciones que no cumplan con dicho criterio se consideran propias del régimen “normal” o de baja volatilidad.
Una vez que se hizo esta selección de datos y que se tienen los parámetros de interés, se utilizan primero las medias y desviaciones para calcular una aproximación del índice de Sharpe (1963). Este índice mide el nivel de rendimiento nominal promedio logrado, dado el nivel de exposición al riesgo. Esto en cada régimen o estado de la naturaleza. El mismo se da por la siguiente expresión, siendo
El objetivo de este análisis es caracterizar y contrastar el desempeño financiero que se tendría en los mercados emergentes, ya sea en su totalidad y diversificación geográfica o ya sea segmentados regionalmente o por bloque (BRIC, por ejemplo).
Estos resultados observados, se contrastan contra el desempeño conjunto de todas las bolsas de valores miembro del S&P global 100 index (países emergentes y desarrollados) y el desempeño de los mercados accionarios estadounidenses al ser este país la principal plaza bursátil en el mundo y al tener la moneda base con la que los índices estudiados son calculados.
Una pregunta natural que surge del procesamiento de datos previamente descrito es la relativa a definir si la serie de tiempo debe ser caracterizada con un modelo markoviano de cambio de régimen como el filtro de Hamilton (1989) o simplemente deben emplearse la media y desviación estándar en un contexto de una función de probabilidad unimodal. Para esto se utilizan los criterios de información de Akaike (1974), Schwarz (1978), Hannan y Quinn (1979), quienes parten del logaritmo de la función (LFF) de verosimilitud planteada en (5):
De manera complementaria al análisis anterior, se generan gráficas de violín para comparar y contrastar el desempeño observado en los rendimientos Δ%Pt de cada índice. Este tipo de análisis es una extensión de las gráficas de caja convencionales en donde se grafican en un cuadro o caja vertical la media, mediana, cuantiles de 5% y 95%, así como los valores máximo y mínimo en una línea.
A diferencia del diagrama de caja convencional, la gráfica de violín divide verticalmente una caja en dos. A la izquierda presenta la caja del régimen s = 2 y a la derecha la del otro régimen. De manera complementaria, presenta los puntos con la observación de todos los rendimientos observados y grafica un kernel gaussiano de cada lado. El kernel de la izquierda es la función empírica de probabilidad de los datos del régimen s = 2 en donde la regla de selección dada en (9) se cumple. El de la derecha corresponde a los datos restantes. Dado quelos dos kernel graficados se sobreponen de cada lado, la representación gráfica toma una forma similar a la de un violín. De ahí el nombre coloquial de la misma. Una vez que se describió cómo es que se han procesado y analizado los datos, se procede a la revisión de los resultados logrados.
ANÁLISIS DE RESULTADOS
En la tabla 3 se presenta un resumen de los parámetros de media y desviación estándar calculados para toda la serie de tiempo y para cada uno de los dos regímenes de interés. De manera complementaria, se presenta el índice de Sharpe observado. Como puede apreciarse con resaltado en gris en dicha tabla, las bolsas de Estados Unidos (SP500) se sugieren como las más rentables durante todo su periodo de estudio, seguidas de las bolsas de Latinoamérica (LATAM) y los países de Europa del Este (EMEURO).
Tabla 3 Resumen de rendimiento medio esperado, desviación estándar e índice de Sharpe de los índices estudiados
| Ticker | Media (serie de tiempo completa) | Media (periodos “normales” S=!) | Media (periodo de crsis s=2 |
|---|---|---|---|
| GLOBAL | 0.0306 | 0.2122 | -0.6272 |
| SP500 | 0.1416 | 0.3327 | -0.1970 |
| EMERGING | 0.0858 | 0.4584 | -0.7453 |
| LATAM | 0.1105 | 0.4796 | -1.9198 |
| ASIAPAC | 0.0027 | 0.1732 | -1.2806 |
| EMEURO | 0.1910 | 0.4864 | -0.7278 |
| MOAFRICA | 0.0780 | 0.3602 | -0.9734 |
| BRIC | 0.0935 | 0.2133 | -0.3250 |
| Ticker | Desviación estándar (serie de tiempo completa) | Desviación estándar (periodos "normales" S=1) | Desviación estándar (periodos de "crisis" S=2) |
| GLOBAL | 2.4307 | 1.6237 | 4.1481 |
| SP500 | 2.3538 | 1.4485 | 3.3911 |
| EMERGING | 2.9269 | 1.8550 | 4.3709 |
| LATAM | 3.9892 | 2.8550 | 7.3685 |
| ASIAPAC | 2.7817 | 1.9742 | 6.0024 |
| EMEURO | 4.2550 | 2.7460 | 7.0546 |
| MOAFRICA | 3.1088 | 2.2831 | 4.9986 |
| BRIC | 3.8470 | 2.5778 | 6.6312 |
| Ticker | Índice de Sharpe (serie de tiempo completa) | Índice de Sharpe (periodos "normales" S=1) | Índice de Sharpe estándar (periodos de "crisis" S=2) |
| GLOBAL | -0.0094 | 0.0977 | -0.1641 |
| SP500 | 0.0374 | 0.1927 | -0.0739 |
| EMERGING | 0.0110 | 0.2183 | -0.1828 |
| LATAM | 0.0143 | 0.1492 | -0.2678 |
| ASIAPAC | -0.0183 | 0.0606 | -0.2223 |
| EMEURO | 0.0323 | 0.1576 | -0.1108 |
| MOAFRICA | 0.0079 | 0.1343 | -0.2054 |
| BRIC | 0.0104 | 0.0620 | -0.0571 |
Tasa promedio semanal del T-bill de 3 meses con 5 días de vencimiento 0.0535
Fuente: Elaboración propia con datos de Reuters.
De manera análoga se aprecian los resultados observados en los dos regímenes. Al aplicar el filtro de Hamilton los resultados cambian, los índices más rentables son los de la zona de Europa del este y Latinoamérica en periodos normales o de volatilidad baja y los Estados Unidos y el bloque de países conocido como BRIC en el periodo de alta volatilidad o crisis.
En línea a lo esperado por los postulados de la Teoría clásica de portafolios, se aprecia, gracias a los efectos de la diversificación, que el índice con menor nivel de riesgo (desviación estándar) corresponde a los Estados Unidos, seguido del índice global. Situación que es de antemano esperada gracias a la amplia diversificación que ambos índices tienen, así como por el hecho de que la mayoría de los inversionistas tienen posiciones en acciones de dicho país, al ser considerado el más seguro y al ser la moneda de Estados Unidos una de reserva.
Una causa que podría dar un sesgo a favor de los Estados Unidos, en términos de rentabilidad y riesgo en el presente trabajo, es el hecho de que todos los índices estudiados están valuados en dólares de dicho país. Dado esto, no se está incorporando el efecto que el riesgo cambiario y la depreciación que algunas monedas emergentes pudieron tener frente al dólar; siendo esta última una moneda de refugio en tiempos de crisis. Con esto en mente, se deja como una sugerencia de futuros trabajos revisar de nuevo los índices estudiados, valuados en otras monedas, para determinar si el efecto cambiario genera los resultados que se aprecian.
A pesar de este resultado, se aprecia que al medir el rendimiento esperado deflactado con el nivel de riesgo por medio del índice de Sharpe, la perspectiva cambia al aplicar el filtro de Hamilton. En específico el índice de los Estados Unidos ya no es el más eficiente en su relación riesgo-rendimiento, sino el índice de países emergentes y el del bloque BRIC en periodos normales y de crisis, respectivamente.
Una pregunta natural que surge del análisis anterior es saber si realmente el filtro de Hamilton es apropiado para el análisis. Esto es, determinar con mayor claridad si se separa en dos regímenes la serie de tiempo. Para esto se empleó el logaritmo de la función de verosimilitud (LFF) expuesto en (11). Esto en los criterios de información de Akaike (1974), Schwarz (1978), Hannan y Quinn (1979).
En la tabla 4 se presentan los valores observados para cada índice en dos escenarios: toda la serie de tiempo y la cuantificación de los mismos con el filtro de Hamilton. Con base en los resultados presentados, se tiene evidencia a favor del empleo del filtro de Hamilton para modelar el proceso estocástico de todas las series de tiempo estudiadas.
Tabla 4 Criterios de información para determinar la bondad de ajuste del filtro de Hamilton
| Ticker | Akaike (Toda la serie de tiempo ) | Akaike filtro deHamilton) | Schwarz (Toda la serie de tiempo) | Schwarz (Filtro de Hamilton) | H-Q (Toda la serie de tiempo ) | H-Q(Filtro de Hamilton) |
|---|---|---|---|---|---|---|
| GLOBAL | -4135.5009 | -4387.3414 | -4130.6985 | -4377.7366 | -4133.6663 | -4383.6723 |
| SP500 | -5815.1660 | -6137.4079 | -5810.0367 | -6127.1493 | -5813.2376 | -6133.5511 |
| EMERGING | -5123.4067 | -5412.6235 | -5118.3058 | -5402.4218 | -5121.4862 | -5408.7826 |
| LATAM | -4372.2094 | -4629.5388 | -4367.1085 | -4619.3371 | -4370.2889 | -4625.6980 |
| ASIAPAC | -2503.9400 | -2704.8361 | -2499.5787 | -2696.1135 | -2502.2396 | -2701.4351 |
| EMEURO | -4215.7163 | -4541.8048 | -4210.6154 | -4531.6031 | -4213.7959 | -4537.9639 |
| MOAFRICA | -4977.1470 | -5180.8463 | -4972.0461 | -5170.6446 | -4975.2265 | -5177.0055 |
| BRIC | -2227.7917 | -2400.5585 | -2223.3849 | -2391.7448 | -2226.0770 | -2397.1290 |
Fuente: Elaboración propia con datos de Reuters.
La tabla 5 presenta las matrices de probabilidades de transición de cada régimen en cada índice, así como los días promedio en que duran los periodos normales y de crisis en cada caso estudiado.
Tabla 5 Probabilidades de transición y duración promedio de cada régimen en los índices estudiados
Fuente: Elaboración propia con datos de Reuters.
Los índices de los Estados Unidos, el BRIC y Asia-Pacífico son los que conservan una duración más prolongada de su periodo “normal”. En el régimen de crisis, los índices que duran menos en el mismo son los índices para Latinoamerica, los países emergentes de la región europea, África y Medio Oriente. Esto lleva, de cuenta nueva, a observar que los índices están valuados en dólares americanos y que deben también valuarse en otras monedas para ver su efecto cambiario y contrastar los resultados hasta ahora observados.
Para finalizar esta sección, se presenta la figura 1 con la gráfica de violín de los datos de los rendimientos observados en cada índice, mismos que están separados o filtrados para cada régimen. En la superficie gris claro se representa el kernel o distribución de probabilidad empírica del régimen o periodo de crisis y en la obscura el del periodo normal o de baja volatilidad. Una característica interesante es que las bolsas de Estados Unidos, África y Medio Oriente, así como el índice global, tienen las campanas más compactas en los periodos de crisis. Así, en el índice global, Estados Unidos y Asia-Pacífico presentan este comportamiento en los periodos normales.
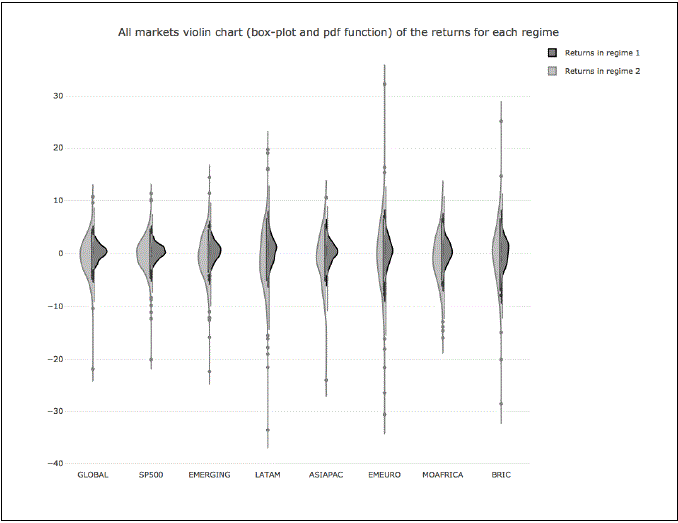
Fuente: Elaboración propia con datos de Reuters.
Figura 1 Gráfica de violín con el resumen estadístico del desempeño de cada índice estudiado, separando el mismo por regímenes
Este resultado agrega una perspectiva adicional, en periodos normales se sostiene lo propuesto por la Teoría clásica de portafolios, existen beneficios de la diversificación para reducir riesgo y variabilidad. Sin embargo, en periodos de crisis, el índice global presenta fluctuaciones adversas a la baja mayores a Estados Unidos. Por otro lado, en las bolsas de los países emergentes sí se cumple lo esperado. En estas últimas, el índice presenta campanas mucho más compactas que cuando se cuantifica el desempeño de cada uno de sus bloques geográficos.
Con base en los resultados alcanzados se puede declarar que el beneficio de la diversificación se sostiene tanto en periodos de crisis como en periodos normales para los mercados considerados emergentes; pero se pierde en periodos de crisis cuando se combinan el desempeño de los índices de países emergentes y países desarrollados. Esto es, el beneficio de la diversificación en un portafolio diversificado globalmente y por tipo de país, se pierde en periodos de alta volatilidad, al valuar en dólares el desempeño observado.
CONCLUSIONES
En el presente trabajo se caracterizó la serie de tiempo de los índices accionarios global, de Estados Unidos, de economías emergentes y por diferentes bloques geográficos de los países miembro de los países emergentes. Los índices estudiados son denominados broadmarketindex o índices de mercado amplio, calculados y publicados por la compañía Standard &Poors Dow Jones LLC, que cuantifican el desempeño del valor de capitalización de los mercados accionarios de los países miembros de cada caso.
En este sentido, la empresa calcula un índice global (S&P global 100), que se compone de índices de capitalización de países considerados tanto desarrollados como de países emergentes, según las métricas establecidas por la propia compañía. Con esto, el citado índice es un portafolio teórico de referencia que incorpora el beneficio de la diversificación en el nivel global, incorporando la interacción (covarianza) y diversificación lograda entre múltiples países, tanto emergentes como desarrollados.
Se observó que uno de los beneficios de invertir de manera diversificada se relaciona con la Teoría de portafolios (Markowitz, 1959, 1956, 1952). En esta se establece que, a mayor cantidad y diversidad de activos financieros en el portafolio, el riesgo específico y el total se reducen de manera importante. Esto se explica con base en el modelo de valuación de activos de capitales (Sharpe, 1963, 1964) conocido como CAPM, por sus siglas en inglés. Dado lo anterior, múltiples trabajos se han hecho para estudiar los beneficios de invertir de manera diversificada en activos de economías emergentes para obtener beneficios de covarianzas negativas y rendimientos esperados más atractivos.
Partiendo de esa perspectiva es que se elaboró esta revisión y se caracterizó en dos regímenes de volatilidad, el desempeño de global 100, S&P 500 de los Estados Unidos, S&P Emergingmarkets, S&P BRIC y los índices regionales del S&P Emergingmarkets, aplicables a los mercados de Latinoamérica, Asia-Pacífico, Europa del Este y Rusia, África y Medio Oriente.
Para caracterizar en dos regímenes, se utilizó el filtro de Hamilton (1989, 1990) con función de verosimilitud gaussiana, empleando el método de cuasi-máxima verosimilitud propuesto por el propio Hamilton (1994). Al aplicar el mismo, se observó que los beneficios de la inversión global diversificada son bajos. Esto último al separar por regímenes o estados de naturaleza (un régimen para periodos “normales”, baja volatilidad o estabilidad y otro para periodos de crisis o alta volatilidad e inestabilidad en los precios).
El resultado observado se debe a que el propio S&P global 100 tiene menores niveles de rendimiento esperado que el S&P de los Estados Unidos y algunos índices de países emergentes latinoamericanos y de Europa del Este. También presenta menores niveles de eficiencia en su relación riesgo y rendimiento, medida con el índice de Sharpe (1964), observándose que la diversificación global no es tan atractiva como se espera, dados los postulados de la teoría de portafolios.
En comparación con el desempeño entre los Estados Unidos y las economías emergentes, el índice global (incluye a otras economías desarrolladas) no presenta mayores beneficios. Por tanto, es mejor un portafolio con dos componentes o grupos: uno para los Estados Unidos y otro para economías emergentes, sin considerar al resto de economías desarrolladas.
Sí se observa un beneficio de invertir con una diversificación geográfica agregada es para las economías emergentes. Los índices geográficos de las economías emergentes de manera individual presentan una mejor eficiencia en su relación riesgo-rendimiento que el índice general. En especial para Europa del Este y Latinoamérica. Sin embargo, el desempeño de su función empírica de probabilidad o kernel en la gráfica de violín, conduce a la conclusión de que los índices individuales tienen una mayor dispersión, tanto en periodos normales como de crisis en compatación con el S&P emergingmarkets que los integra.
Si bien es cierto que, al comparar el desempeño de los países emergentes con el índice global, no se tienen diferencias significativas, sí es de resaltar que una diversificación en el nivel global (incluyendo todos los mercados desarrollados y emergentes en el mismo portafolio) no lleva a reducciones significativas de los niveles de dispersión o riesgo. Esto conduce a concluir que los índices de economías emergentes pueden formar parte de un portafolio al diversificarse con acciones de los Estados Unidos, exclusivamente.
Como nueva línea de investigación se tiene al análisis y valución de los índices en otras divisas, e incluso, empleando índices en moneda locales. Algunos países desarrollados (como los europeos o Japón) tuvieron depreciaciones importantes de sus monedas en relación al dólar de los Estados Unidos, durante algunos periodos de estudio (en especial los de crisis) y esto puede tener una repercusión importante en el desempeño medido y en las conclusiones.
Otras funciones de verosimilitud y el estudio de más regímenes en el proceso estocástico de la serie de tiempo de los índices puede ser también de interés para ampliar los resultados aquí logrados.











 nueva página del texto (beta)
nueva página del texto (beta)