1. Introducción
La navegación autónoma es un problema que ha capturado mucho interés actualmente debido a que ya es una realidad presente en los vehículos totalmente autónomos [1]. Los enfoques para generación de trayectorias son un aspecto estudiado en los centros de investigación y universidades, y precisamente esa temática se aborda en el trabajo presentado en este artículo. Se utilizarán herramientas de la robótica para abordar el problema.
Los vehículos para ser considerados autónomos deben ser capaces de desplazarse en diferentes lugares con poca o nula intervención humana, para ello deben tener la capacidad de decidir qué ruta tomar hacia la posición o trayectoria deseada, a la vez que evita colisionar con obstáculos [2]. Existen distintas metodologías para resolver este problema, sin embargo, una que llama la atención por simplicidad matemática es la teoría de campo potencial [3]-[4]. Los campos de velocidad para guiado de robots se han estudiado a través de ecuaciones de hidrodinámica [5]. Lo que se plantea en este proyecto es estudiarlos desde un enfoque más propio de la robótica, utilizando herramientas de esta última área de estudio, para abordar el problema de una manera más sencilla y entendible.
Campo potencial (potential field). El enfoque estándar de campo potencial artificial se basa en la aplicación del gradiente negativo de una función potencial artificial (APF) como entrada de control para conducir a un vehículo a una posición deseada. Este método es particularmente atractivo debido a su elegancia matemática y simplicidad [3]. Para lograr un guiado más flexible, se han propuesto diferentes leyes de control basadas en el método de campo vectorial. Otro aspecto importante en la generación de trayectorias es la evasión de colisiones.
2. Antecedentes
Muchas estrategias para evasión de colisiones se basan en campos potenciales [6], como la función repulsiva convencional, la cual es adecuada para implementación en tiempo real ya que sólo requiere información del gradiente local y no requiere información global [7]. Sin embargo, su principal desventaja es la presencia de mínimos locales que pueden ocasionar que el vehículo no llegue a la posición meta [2]. Para mejorar el esquema repulsivo básico, han surgido diferentes métodos basados en campos potenciales. Algunos ejemplos de esto son: el método de Objetivos No Alcanzables con Obstáculos Cercanos (GNRON) [8], Funciones Potenciales Harmónicas (HPF) [2], Campo Potencial Híbrido [9], Campos Potenciales Artificiales Evolucionarios [10] y el Campo de Potencial Artificial Mejorado [11]. Una manera de evitar la principal desventaja de los campos estáticos, a saber, la presencia de mínimos locales que imposibiliten la realización de la tarea es la utilización de campos potenciales de velocidad [2]. Mediante esta técnica, es posible utilizar la teoría hidrodinámica para crear un campo evasivo que evite colisiones de una manera más adecuada y natural. De acuerdo con esta información, existen algunos campos de oportunidad en el desarrollo de un control de seguimiento de trayectorias generadas por el método de campos de velocidad.
Como se puede ver en los trabajos mencionados anteriormente el problema de navegación en los vehículos autónomos ha sido y continúa siendo del interés de la comunidad científica, la cual ha propuesto variedad de soluciones aplicadas en distintos tipos de vehículos. En este trabajo se aplica la bien conocida técnica de navegación basada en campos de velocidad en un vehículo con ruedas tipo unicilo para que realice una ruta preestablecida. Las principales contribuciones de este trabajo radican en el estudio e implementación de un control de seguimiento basado en campo de velocidad con evasión de obstáculos para un vehículo autónomo tipo uniciclo, la integración de los componentes de la plataforma experimental y la validación en simulación numérica y también experimentalmente del método estudiado.
El resto del documento está organizado de la siguiente manera: El modelo cinemático del robot móvil, la generación de trayectoria atractiva y evasiva por campos de velocidad, además de la estrategia de control se describen en la sección 3. En la sección 4 se presentan los resultados obtenidos tanto en simulación como experimentalmente. Finalmente, las conclusiones y trabajo futuro se establecen en la sección 5.
3. Metodología
Para generación de trayectorias se utilizará el enfoque de campos potenciales de velocidad. Una vez que se tienen los campos de velocidad de acercamiento y evasivos, se deben obtener sus derivadas temporales, que servirán como referencias al controlador de seguimiento de trayectoria implementado en el vehículo. Como controlador para el vehículo se propone utilizar un simple control PD de velocidad, el cual demuestra ser asintóticamente estable para seguimiento de trayectorias. Se probaron los resultados mediante simulación y se implementaron experimentalmente en el robot móvil AmigoBot.
3.1 Modelo cinemático del Robot Móvil Rodante
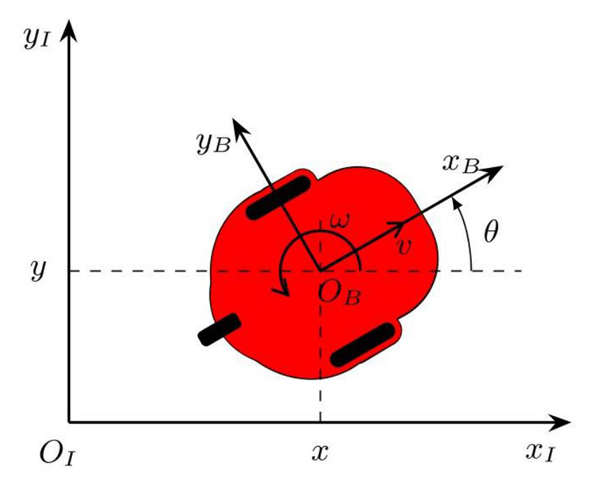
Considere un robot móvil con ruedas (WMR), del tipo uniciclo como el de la Figura 1.
Se asume que el plano de cada rueda es perpendicular al suelo y que la
restricción de movimiento entre las ruedas y el suelo es de puro
rodamiento no deslizamiento, es decir, la velocidad del centro de
masa del robot es ortogonal al eje de las ruedas. La posición del robot en un
marco Cartesiano {I} se especifica completamente mediante el
vector de coordenadas generalizadas
El modelo cinemático más comúnmente utilizado para representar el movimiento de un robot tipo uniciclo está dado por
donde
3.2 Generación de trayectoria atractiva por campos de velocidad
El objetivo del método de campos de velocidad en este caso en particular es
seguir una trayectoria predeterminada. Para generar un campo de velocidad en
trayectoria circular, es necesario calcular dos campos vectoriales, el
campo de aproximación
Para calcular el campo de aproximación, es necesario encontrar el punto más cercano desde cualquier punto del espacio de trabajo hacia la trayectoria. Este punto cercano es calculado por
donde
donde
donde
El ángulo
Tomando las Ecuaciones (5)-(6) para calcular
El campo de aproximación se define como
Denotemos el vector de las derivadas parciales de
El campo de velocidad
donde
3.3 Campo de velocidad para evasión de obstáculo
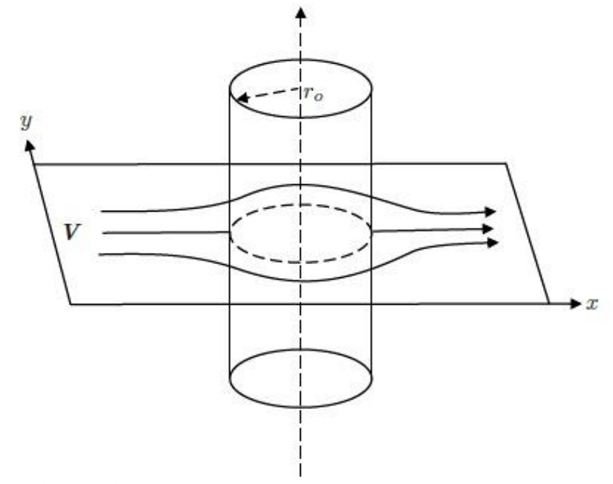
La evasión de obstáculos se logra mediante el uso de la teoría hidrodinámica, específicamente mediante el flujo ideal generado alrededor de un cilindro, como se muestra en la Figura 2.
Definimos el flujo de un fluido plano en estado estacionario, mediante un campo de velocidad
en el punto
es la posición central del obstáculo, con radio
donde
Usando un obstáculo circular, el cual interfiere con el campo de flujo vectorial,
donde
La función potencial de velocidad propuesta para un fluido ideal alrededor de un obstáculo circular es
Donde
es el ángulo del vector de campo de velocidad en ese punto. La velocidad de flujo
alrededor del cilindro está definida como el gradiente de la función
Entonces, la componente
donde
Entonces, el vector velocidad para la maniobra evasiva es
Una forma de visualizar el efecto del campo evasivo es redireccionar la dirección del vector del campo atractivo, redirigiendo la referencia de velocidad para intentar rodear el obstáculo. Por lo tanto, el vector de velocidad evasiva remplaza el vector de velocidad previo, y también se normaliza mediante
este vector de velocidad se definió mediante coordenadas rectangulares
Note que el vector de velocidad V está dado por (11) en ausencia de obstáculos en el ambiente de trabajo. Posteriormente, el vector de velocidad es actualizado de manera iterativa empleando (17)-(21) por cada obstáculo en el ambiente.
3.4 Estrategia de control
En las Ecuaciones (1) que expresan
el modelo cinemático del WMR, las velocidades del robot móvil están relacionadas
con el vector de velocidad lineal y angular
A partir del campo de velocidad generado
El ángulo dado por el vector de velocidad
por lo que, para hacer un control de seguimiento de velocidad angular, se debe
obtener primero la derivada del vector
Finalmente, el control de velocidad estará dado por
4. Resultados y Discusiones
4.1 Simulación
Para realizar la simulación numérica se utilizaron funciones de solución de ecuaciones diferenciales ODE de MATLAB. La simulación consistió en lo siguiente. Se supone una postura inicial del vehículo, es decir posición y orientación inicial, se supone también un obstáculo de radio y posición conocidas. El objetivo es realizar una trayectoria circular moviéndose a velocidad constante. Partiendo de estos datos conocidos, el programa grafica las líneas de flujo de campo de velocidad que atraen el vehículo a la trayectoria deseada mientras rodea los obstáculos. Finalmente se desarrolla la simulación del movimiento del vehículo desde su postura inicial hacia la trayectoria deseada.
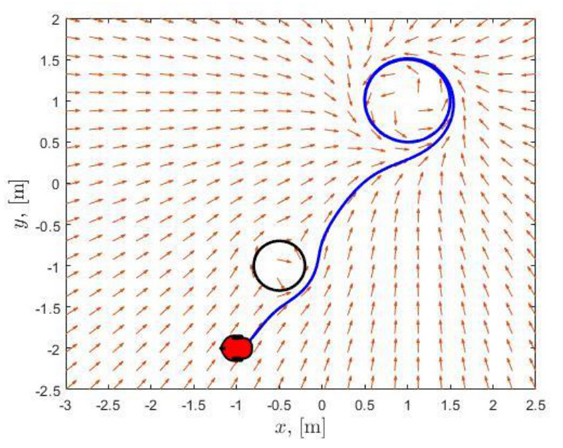
La Figura 2 muestra el resultado de
simulación del vehículo dentro del campo de velocidad generado, el cual lo atrae
desde cualquier posición inicial hacia la trayectoria circular, evitando
cualquier obstáculo que interfiere su trayecto. En dicha simulación la postura
inicial del vehículo es x(0)=-1, y(0)=-2, θ(0)=0. La trayectoria es un círculo
centrado en el punto (1,1) y de radio
De la Figura 3 se logra observar que el vehículo alcanza perfectamente la trayectoria circular deseada a la vez que evade el obstáculo que se encuentra en el camino hacia ella.
4.1 Resultado experimental
Para llevar a cabo la realización experimental, se utilizó la plataforma de robot móvil Amigobot, de la marca Mobile Robots. La captura de movimiento se realizó mediante un sistema de visión Optitrack de 6 cámaras Flex 13. Se desarrolló una interfaz en Simulink para la implementación del control propuesto. Simulink tiene la ventaja de que al mismo tiempo puede leer la información de posición obtenida mediante el sistema de visión, realizar todos los cálculos necesarios para formular el campo de velocidad y traducirlo a consignas de velocidad, y finalmente enviar dichas consignas inalámbricamente al vehículo.
Una vez generadas las consignas, estas son enviadas mediante comunicación Wi-Fi al robot, para lograr esta comunicación se empleó la librería de programación Aria del fabricante, esta librería se ejecuta sobre la plataforma ROS (Robot Operative System).
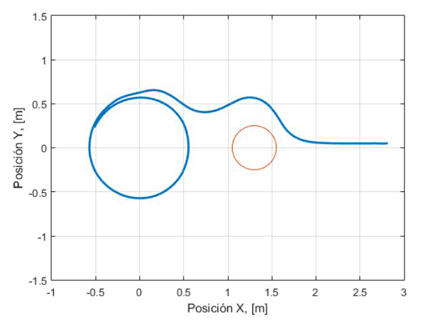
Como experimento se propuso que el robot móvil, partiendo de una posición
inicial, realice una trayectoria circular, donde el círculo de referencia está
centrado en el origen, con radio 0.5 m. Se consideró un obstáculo que interfiere
la trayectoria del vehículo, con coordenadas (1.6,0) y radio
5. Conclusiones
La teoría de campos potenciales de velocidad prueba ser muy efectiva tanto en la generación de trayectorias, así como evasión de obstáculos, debido a que genera referencias continuas que son fáciles de seguir mediante un controlador de seguimiento. El arreglo experimental que se tiene implementado en las instalaciones de Ingeniería Electrónica en la Universidad de Sonora es muy sencillo de utilizar y permite probar controladores de forma muy similar a las simulaciones. Esto abre la puerta a futuras mejoras y aplicaciones en áreas como la navegación autónoma, la robótica colaborativa y la interacción humano-robot. Usando el arreglo experimental se evaluó el desempeño del algoritmo de navegación estudiado. Los resultados obtenidos tanto en simulación como experimentalmente demuestran el cumplimiento de la tarea con el esquema de navegación y control propuesto.
Como trabajo futuro, se tiene previsto escalar la propuesta presentada a un esquema de múltiples agentes, donde se explorarán diversas estrategias, como la formación y el trabajo colaborativo entre vehículos. Además, se pretende implementar la generación de campos de evasión en tiempo real, con el objetivo de lograr una evasión eficiente de obstáculos variables, es decir, obstáculos que cambien de posición con el tiempo.











 nueva página del texto (beta)
nueva página del texto (beta)