Contextualização e Estado-da-arte
Conforme já discorrido por renomados geodesistas, tais como Hofmann-Wellenhof e Moritz (2006), Torge e Müller (2012) e Gemael (2012), o objetivo primordial da Geodésia é determinar a forma e a dimensão da Terra, bem como do campo da gravidade em seu exterior e suas variações temporais. Entretanto, ao longo das últimas décadas este objetivo tem passado por drásticas mudanças, principalmente devido à evolução das técnicas aplicadas em observações e dos métodos computacionais empregados em seu processamento. Concomitantemente a estes avanços, os problemas clássicos da Geodésia foram expandidos, e sua função primária de medição da superfície terrestre foi ampliada para a detecção dos efeitos de mudanças globais e da geodinâmica (Drewes, 2006).
Este entendimento traz à tona a necessidade de compreensão de entes físicos ligados diretamente à maneira como a superfície terrestre se dispõe e se modifica ao longo do tempo, gerando uma compreensão de como o Sistema Terra se comporta e trazendo consigo a possibilidade de monitorá-lo de modo contínuo. No entanto, para que isto seja possível, não apenas as observações contínuas são necessárias, mas também sua vinculação a um Sistema Geodésico de Referência Global.
Quando se trata de informações altimétricas, conforme preconizado por IAG (2015), a busca pela definição de um Sistema Vertical de Referência Global (do inglês, International Height Reference System-IHRS) deve ser realizada tomando-se como referência uma superfície equipotencial do campo da gravidade, com valor de geopotencial W 0 = 62.636.853,4 m 2 s −2 . Adicionalmente, IAG (2015) determina que as coordenadas verticais primárias para tal sistema de referência sejam definidas com base no número geopotencial C P , expresso conforme a Equação 1, na qual W 0 representa o valor do geopotencial na superfície de referência e W P representa o valor do geopotencial no ponto de cálculo.
Estas considerações supramencionadas são possíveis, na atualidade, devido principalmente a avanços tecnológicos ocorridos nas últimas décadas. Graças ao surgimento de modernas técnicas de análise do campo gravitacional, aliado ao precípuo desenvolvimento analítico e matemático segundo formulação adequada, não há mais a dependência de observações de campo ou observações terrestres como fonte única de dados. Um exemplo desta modernização pode ser visualizado nas informações obtidas de missões espaciais, algumas das quais têm por objetivo determinar as perturbações nas órbitas dos satélites. Estas perturbações são induzidas pelo efeito gravitacional de heterogeneidades de massas relativamente a uma distribuição esférica homogênea, gerando conhecimento das anomalias associadas às feições de longos e médios comprimentos de onda deste campo, e completadas com informações de curtos comprimentos de outras fontes. Quando associadas ao potencial centrífugo, viabilizam o estabelecimento de Modelos Globais do Geopotencial-MGGs (Melo, 2011).
Os MGGs são gerados a partir de um conjunto de coeficientes do desenvolvimento do potencial gravitacional em série de funções harmônicas esféricas. Todo esse arcabouço de informações, por fim, propicia a realização de determinações para implantação do IHRS, ao qual as observações altimétricas devem estar vinculadas.
No entanto, tais modificações e avanços não vêm a depor totalmente contra os dados altimétricos já existentes em cada país. A integração entre estes dados já coletados pelos órgãos competentes, visando à adequação à nova modelagem vertical e a eliminação de discrepâncias entre os data verticais nacionais e o datum vertical global, pode ser realizada conforme a formulação apresentada pela Equação 2, como adaptado de Santacruz Jaramillo et al. (2016), expressa em função da diferença entre os números geopotenciais de um ponto de cálculo P obtidos segundo o datum global (CP) e o datum nacional (CPi).
Note que o desenvolvimento da diferença de números geopotenciais à esquerda da Equação 2 culmina na diferença dos termos I e II. O termo I contém a diferença entre o geopotencial de referência W 0 e a soma do esferopotencial U P em um ponto de interesse P e o potencial perturbador T P no mesmo ponto P - o primeiro é padronizado, como já descrito neste mesmo item; para o segundo, há fácil equacionamento matemático; para o terceiro, busca-se alternativas na atualidade para sua determinação plena - por meio da solução do Problema de Valor de Contorno da Geodesia (PVCG) - em pontos da superfície. Já o termo II contém o somatório de j produtos discretos entre valores médios da gravidade g m e desníveis ∆n, característicos de conjugação de operações de nivelamento e gravimetria, formando a parte prática da equação. Dessa forma, considerando-se a existência de uma rede de nivelamento com densidade adequada e conjugada com informações de gravimetria ao longo de seu levantamento, é possível unir este conhecimento prático à modelagem matemática teórica cabível e proporcionar o alinhamento com parte das recomendações que buscam a definição do IHRS.
No que diz respeito à integração brasileira a esta tendência mundial, verifica-se carência na união entre prática e teoria. Atualmente, a Rede Altimétrica Fundamental Brasileira (RAFB) - denominada Rede Altimétrica de Alta Precisão (RAAP), mantida pelo Instituto Brasileiro de Geografia e Estatística (IBGE) e vinculada ao Sistema Geodésico Brasileiro (SGB) conta com aproximadamente 69.859 estações de altitudes normais-ortométricas (altitudes obtidas por nivelamento geométrico e corrigidas do não-paralelismo das superfícies equipotenciais do campo da gravidade) conhecidas, distribuídas ao longo do território nacional (IBGE, 2011). Todavia, a maneira não-uniforme com que se distribui, a inexistência de vínculo de parte da rede com o Datum Vertical Brasileiro em Imbituba (DVB-I) e a existência de grande quantidade de ramais, os quais impossibilitam o ajustamento das altitudes trazem à tona um problema maior do que a aparentemente simples conversão e adequação às recomendações do IHRS vindouro: as deficiências atuais da RAFB. É possível verificar que, na Região Amazônica, deve haver um esforço para preenchimento de informações altimétricas, visando a uma melhor solução para o alinhamento ao IHRS.
Surge, então, a perspectiva de modelagem das altitudes normais-ortométricas H NOrt nas regiões de vazio tomando por base altitudes elipsoidais h - provenientes de observações GNSS (Global Navigation Satellite System) discretas - e valores de altitude normal-geoidal η - provenientes de cálculo de funcionais de MGGs. Esta modelagem baseia-se na resolução da Equação 3, descrita como método absoluto, e cujos termos já foram definidos para um dado ponto P (Gemael, 2012).
Como o enfoque principal deste trabalho reside na determinação de altitudes normais-ortométricas, em consonância com a RAFB, uma outra observação deve ser feita a seu respeito e sobre o exposto na equação 3. Conforme abordado por Ferreira et al. (2013), o fato do comportamento das altitudes normais-ortométricas não apresentarem um significado completamente físico faz com que estas estejam referidas a uma superfície de referência diferente das usuais geoide e quasi-geoide. Em virtude disso, a referência supracitada descreve a dependência entre as altitudes elipsoidais e as altitudes normais-ortométricas aos moldes da Equação 3, na qual η é por eles denominada como altitude normal-geoidal, em analogia à altitude normal-ortométrica.
Uma representação da equação 3 é apresentada na porção à esquerda da Figura 1, a qual descreve a relação entre as variáveis supramencionadas para o ponto P em questão e considerando a melhor modelagem da altitude normal-geoidal η pela própria altitude geoidal N.
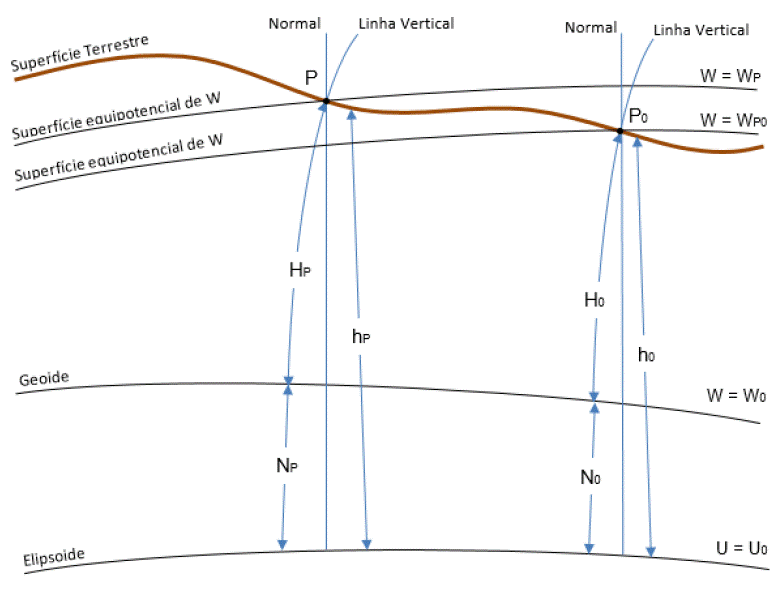
Fonte: Nicacio, 2017
Figura 1 Modelagem altimétrica baseada em altitude elipsoidal e altitude geoidal.
Todavia, chama-se a atenção para o seguinte fato: tanto os MGGs que dão origem às
funcionais utilizadas para modelar altitudes normais-geoidais desejadas, quanto
outros modelos de ondulação geoidal, como o nacional MAPGEO2015, contêm erros
inerentes a seu sistema de processamento e a seu modo de obtenção na forma:
Ainda, a já mencionada Figura 1, quando analisada por completo, traz a representação da relação apresentada na Equação 4, novamente considerando a modelagem da altitude normal-geoidal η pela altitude geoidal N.
Por fim, frisa-se que a alternativa apresentada anteriormente é reforçada por Sánchez (2016), principalmente sob o aspecto de consecução de sistemas de referência vertical. Segundo adaptado desta referência, as atuais técnicas geodésicas, principalmente aquelas apoiadas por posicionamento e navegação satelital, apresentam requisitos de precisão superiores àqueles propiciados pela Equação 3. Sendo assim, a utilização do método relativo para correlacionar altitude elipsoidal e altitude normal-ortométrica com a altitude normal-geoidal, conforme reescrito na Equação 5, deve ser utilizado para fins de maior precisão e para a viabilização de modernos e precisos sistemas de referência vertical.
Desta forma, a abordagem de determinação de altitude normal-ortométrica pelo método relativo, com o uso de observações GNSS discretas e informações geoidais provenientes de Modelos Globais do Geopotencial, apresenta grande potencial de solução para a densificação da RAFB na região da Amazônia Legal Brasileira e, consequentemente, para viabilizar o alinhamento da rede ao IHRS e sua conveniente materialização. Justifica-se, portanto, a realização do presente trabalho, que visa a verificar a possibilidade e a viabilidade da referida abordagem para a área estudada.
Materiais e métodos
Dados altimétricos e GNSS
Conforme discorrido por IBGE (2017), o SGB (Sistema Geodésico Brasileiro) é composto fundamentalmente pelas redes vertical, horizontal e gravimétrica. Com o advento das tecnologias espaciais de posicionamento, estas redes abrangem na atualidade todo o território nacional. No que diz respeito à rede planimétrica, uma de suas vertentes, na atualidade, é a rede geodésica composta por estações SAT-GPS, ou seja, estações cujas coordenadas foram determinadas por meio de rastreio e obtenção de informações da constelação GPS. Ainda segundo a referência citada, a rede SAT-GPS fornece um referencial com abrangência nacional para usuários que precisem de informações posicionais para diversos fins, como apoio ao mapeamento, demarcação de unidades político-administrativas, obras de engenharia, regulamentação fundiária, posicionamento de plataformas de prospecção de petróleo, delimitação de regiões de pesquisas geofísicas, entre outros. Além de informações planimétricas, as estações GNSS fornecem também coordenadas altimétricas referenciadas ao elipsoide - as altitudes elipsoidais.
Optou-se por realizar o acesso às informações geoespaciais por meio do Visualizador da INDE (Infraestrutura Nacional de Dados Espaciais, 2016) principalmente por ser possível realizar o download das referidas informações em formato shapefile. Esta característica possibilitou integração com ferramentas de geoprocessamento, como o software QGIS, a realização de operações espaciais com os dados, como recorte e interseção conforme necessário, e a fácil exportação das informações shapefile para outros formatos, em vistas de integrá-las a algoritmos desenvolvidos pelo autor.
Para a obtenção de dados da RAFB, também foi utilizado o Visualizador da INDE, com operação similar e visando a alcançar as vantagens já citadas. Um detalhamento sobre quantos e quais pontos foram utilizados no desenvolvimento da pesquisa é fornecido no item que discorre sobre área de estudo e área-teste.
Modelos Globais do Geopotencial empregados e o Modelo Geoidal Nacional
O primeiro modelo baseado não apenas na solução de estimativas de um conjunto de anomalias de gravidade provenientes de observações de órbitas satelitais, mas também provido de observações gravimétricas, observações sobre a topografia do terreno e de altimetria por satélite foi o EGM2008 (Pavlis et al., 2012). Este modelo foi considerado revolucionário à época de sua elaboração e lançamento, devido à grande quantidade de informações utilizadas para geração dos coeficientes de seu desenvolvimento em harmônicos esféricos e, consequentemente, de seu possível desenvolvimento até grau 2159, sendo completado em zonais até grau 2190. Levando em consideração esta mesma característica, foram selecionados para emprego no presente trabalho modelos combinados - ou seja, que integram informações gravitacionais derivadas de estudo de órbitas satelitais, informações de gravimetria terrestre e informações de altimetria por satélite - com possibilidades compatíveis com as do modelo EGM2008, principalmente no que diz respeito ao alto grau de desenvolvimento e à alta resolução espacial. A lista e as características dos modelos utilizados encontram-se na Tabela 1. Na dissertação, é realizada uma descrição detalhada sobre cada um dos modelos, a qual é omitida do presente artigo mas pode ser verificada em Nicacio e Dalazoana (2017).
Tabela 1 MGGs utilizados no trabalho
| Modelo | Grau/Ordem empregados | Ano |
| XGM2016 | 719 e 360 | 2017 |
| GOCO05C | 720 e 360 | 2016 |
| GGM05C | 360 | 2016 |
| EIGEN-6C4 | 2190, 720 e 360 | 2014 |
| EGM2008 | 2190, 720 | |
| e 360 | 2008 |
Fonte:adaptado de Nicacio (2017).
Reforça-se que, além das justificativas ora apresentadas, embasa-se esta escolha com resultados e desempenhos positivos para modelos combinados, em especial o próprio EGM2008, em estudos ao longo de todo o planeta, tais como Arábia Saudita (Al-Ghamdi; Dawod, 2014), Alemanha (Voigt; Denker, 2015), Polônia (Godah et al., 2015), América do Sul (Matos et al., 2015), África (Abd-Elmotaal, 2015) e, nacionalmente, na Amazônia oriental (Moreira, 2015).
Para a obtenção de extratos de funcionais dos MGGs a partir do serviço de cálculo no sítio do ICGEM (International Centre for Global Earth Models), organização responsável por armazenar, gerir e disponibilizar os modelos ao usuário, optou-se por uma abordagem ponto-a-ponto em detrimento de uma geração em grade e posterior interpolação, a fim de preservar a precisão e as características de cada modelo. Para tanto, foi desenvolvida e empregada a ferramenta SPGG - Single Point GEM [Global Earth Models] Generator, uma aplicação standalone capaz de gerar extratos dos modelos globais do geopotencial de forma pontual, utilizando uma lista de pontos elaborada e formatada pelo usuário e com a interação direta com o serviço web do ICGEM (Nicacio, 2016).
Adicionalmente ao uso dos MGGs, utilizou-se para modelagem da altitude normal-geoidal o modelo geoidal nacional MAPGEO2015, elaborado em conjunto pelo IBGE e pela EPUSP-Escola Politécnica da Universidade de São Paulo, fruto de mais de duas década de cooperação e de melhorias de versões anteriores. Trata-se de um modelo de ondulação geoidal disponibilizado juntamente com um sistema de interpolação que possibilita aos usuários a obtenção de altitude geoidal em um ponto ou em um conjunto de pontos do território nacional a partir de suas coordenadas. Sua abrangência cobre a área compreendida pelas latitudes 6 °N e 35 °S e pelas longitudes 75°W e 30°W, referenciadas ao SIRGAS 2000 (IBGE, 2015). Apesar de, claramente, uma análise do exposto em relevantes trabalhos, como IBGE (2015) e Blitzkow et al. (2016), demonstrar que o MAPGEO2015 apresenta melhorias significativas em relação ao MAPGEO2010, adequando-se com precisão centimétrica ao território nacional e em média apresenta diferença nula com valores reais, sua utilização neste trabalho se dá em forma de avaliação e comparação com os MGGs atuais. Isto porque trabalhos anteriores, tais como Melo (2011) e Jamur et al. (2010), demonstram baixa aderência do modelo geoidal nacional em determinadas regiões do país, em detrimento de uso de MGGs. Adicionalmente, a carência de outros trabalhos acadêmicos empregando e avaliando o uso do MAPGEO2015 estimulam seu uso no presente trabalho.
Área de estudo e área-teste
Conforme já abordado anteriormente, a área de estudo do presente trabalho é a Amazônia Legal Brasileira. Trata-se de uma área de cerca de 5 milhões de quilômetros quadrados -correspondendo a aproximadamente 59% do território brasileiro- e que, atualmente, corresponde à área dos Estados da Região Norte do Brasil, acrescidos da totalidade do Estado de Mato Grosso e dos municípios do Estado do Maranhão situados a oeste do meridiano 44 °O. Todavia, no que diz respeito à existência de estações que atendam aos pressupostos apresentados até o momento, a área de estudo conta com 154 estações SAT-GPS que possuem conexão com a RAFB - doravante denominadas estações GNSS-RN, distribuídas de forma não-homogênea e perfazendo a área de estudo de referência inicial, conforme Figura 2.
Entretanto, levando-se em consideração a baixa confiabilidade e disponibilidade de dados na área de estudo para fomentar a elaboração de uma metodologia consistente - entenda-se: baixa vinculação à RAFB, encontrando-se em sua maioria em ramais da rede; baixa precisão das altitudes normais-ortométricas; entre outros óbices - julgou-se cabível a adoção de uma área-teste consistente. Esta área-teste foi o estado do Paraná, o qual contava inicialmente com 32 estações GNSS/RN distribuídas de maneira não-uniforme, conforme Figura 3.
Como, novamente, a elaboração da metodologia poderia ser prejudicada pela não-homogeneidade das estações, realizou-se um procedimento para identificação e seleção de estações baseado em coerência entre mútuas distâncias quando comparadas às resoluções espaciais dos MGGs empregados e em análise de suas precisões altimétricas (Nicacio, 2017). Para exemplificar, tome-se como exemplo a obtenção de extratos de MGG com grau máximo de desenvolvimento 720, cujas resoluções seriam, consonante Seeber (2003, p. 469) da ordem de 20.000/720, aproximadamente igual a 27,78 km. Assim, estações GNSS/RN que distem menos de 27,78 km entre si devem ser eliminadas, com exclusão daquelas que possuírem menores precisões.
Destarte, seguindo estes critérios, a quantidade de estações na área-teste de referência final utilizada no presente trabalho foi subdividida da seguinte forma: foram utilizados 22 pontos para modelos desenvolvidos até grau 360, 27 pontos para modelos desenvolvidos até grau 720 e 29 pontos para modelos até grau 2190.
Ainda, para a área de estudo e para a área-teste, foi identificado um conjunto de pontos denominado área desejada, na qual deseja-se realizar a determinação das altitudes normais-ortométricas por meio da estratégia elaborada. A área de estudo desejada é composta por 602 estações SAT-GPS, ao passo que a área-teste desejada é composta por 127 estações da mesma rede.
Estratégia para determinação de altitudes normais-ortométricas
Para fins de elaboração da estratégia, foram usadas três vertentes distintas de análise para determinação das altitudes normais-ortométricas: a) utilização dos métodos absoluto e relativo para determinação altimétrica; b) utilização de extratos dos MGGs obtidos em diferentes graus de desenvolvimento e do MAPGEO2015; e c) utilização das funcionais altitude geoidal e anomalia de altitude para modelagem de altitude normal-geoidal. Em cada uma delas, elencou-se como mais vantajosa aquela que minimizava o módulo da discrepância entre os valores de altitude normal-ortométrica de referência (H NOrt ref ), já possuídos pelos pontos, e os valores calculados (H NOrt calc ) por meio das vertentes anteriores.
Por exemplo, para fins da comparação entre os métodos absoluto e relativo, considerando-se que as altitudes normais-ortométricas são determinadas pelo método absoluto por intermédio da equação 3, ao passo que estas são determinadas pelo método relativo por intermédio da equação 4, considerou-se com melhor desempenho aquela que tornou verdadeira a expressão Equação 6.
Cada vertente foi analisada individualmente com vistas a escolha das melhores opções para a estratégia consolidada. Adicionalmente, por ocasião do uso do método relativo, tal como apontado por Nicacio (2017), dentre os possíveis limitantes para o posicionamento do ponto P 0 , optou-se por adotar aquele posicionado de forma mais centralizada na área do conjunto de pontos considerado, para fins de homogeneização das linhas de base desta determinação.
Principais resultados obtidos
Resultados para a área-teste
Através dos estudos realizados para a área-teste, foi possível atestar os principais resultados conforme gráfico apresentado na Figura 4. Neste gráfico, as discrepâncias médias por conjunto de pontos, obtidas por meio do método relativo são representadas por linhas contínuas, ao passo que aquelas obtidas pelo método absoluto são representadas por linhas tracejadas. Na legenda do gráfico, estão destacados no retângulo magenta as representações obtidas pela funcional altitude geoidal e no retângulo ciano aquelas obtidas pela funcional anomalia de altitude.

Fonte: Nicacio, 2017
Figura 4 Gráfico de diferenças médias, em metros, para método absoluto e relativo por grau de desenvolvimento dos modelos na área-teste.
Da figura em questão, pode-se verificar que o desempenho do uso do método relativo é, conforme esperado deveras superior ao uso do método absoluto para os MGGs; Este padrão, no entanto, não é conservado pelo MAPGEO2015. Adicionalmente, não há padrão de comportamento no tocante às diferentes funcionais do geopotencial para modelagem da altitude normal-geoidal, bem como não há escolha crassa para uso de distintos graus de desenvolvimento - exceção feita para extratos desenvolvidos até grau 360, os quais tiveram desempenho aquém do esperado.
Observe-se, ainda, na Figura 4, a existência de uma configuração que minimizou a discrepância média do conjunto de pontos ao qual ela foi aplicada, da forma da Equação 7, na qual há o cálculo da discrepância individual θ i para cada um dos i pontos de um conjunto de n pontos. Esta configuração foi denominada “configuração ótima” e, para este conjunto de pontos, foi o MGG GOCO05C, desenvolvido até grau 720 e segundo a funcional anomalia de altitude. Com esta configuração, obteve-se discrepância média θ m = 0,0904 m = 9,04 cm.
Para a área-teste pode-se, por fim, elaborar a Tabela 2, a qual demonstra os ganhos impostos pela utilização da metodologia alternativa, que contempla o uso dos MGGs em sua configuração ótima associados ao método relativo, em comparação a uma metodologia denominada tradicional, que contempla o uso do MAPGEO2015 associado ao método absoluto. Estas estimativas finais foram realizadas após uma fase de identificação visual e eliminação de outliers, ou seja, pontos cuja modelagem não foi bem executada segundo nenhuma das configurações utilizadas.
Tabela 2 Comparativo entre metodologia proposta e metodologia tradicional na área-teste
| Metodologia alternativa | Metodologia tradicional | |||||
| θ (m) | σθ 2 (m²) | σθ (m) | θ (m) | σθ 2 (m²) | σθ (m) | |
| Máxima | 0,1487 | 0,0015 | 0,0393 | 0,5304 | 0,0118 | 0,1085 |
| Média | 0,0621 | 0,1678 | ||||
| Mínima | 0,0005 | 0,0022 | ||||
Fonte: Nicacio (2017).
Sendo assim, os ganhos da aplicação da metodologia ora proposta foram reais e de grande significância para a aplicação da estratégia alternativa, sendo em média superiores a 10 centímetros para a área-teste. Estes resultados apontaram no sentido de refinamento da metodologia utilizada, elaboração de uma metodologia consolidada e sua precípua aplicação na área de estudo.
Estratégia alternativa consolidada
Da análise da Figura 4, bem como de outras análises realizadas, verificou-se os tópicos apresentados a seguir. Estes foram considerados por ocasião da elaboração da estratégia alternativa consolidada, aplicável à área de estudo e extensível a demais áreas onde se almeje realizar abordagem similar.
O uso do método relativo é comprovadamente mais adequado que o método absoluto para manipulação dos MGGs; estes devem, portanto, incorporar a estratégia definitiva;
A partir de todo o conjunto de pontos disponíveis em uma determinada área, deve ser mantida a seleção e priorização de pontos para homogeneização de dados, segundo diferentes graus de desenvolvimento dos extratos dos MGGs e suas resoluções espaciais;
Em virtude de seu desempenho aquém do esperado e de sua inadequação para uso segundo os pressupostos do método relativo, a funcional altitude geoidal obtida por meio do modelo geoidal nacional MAPGEO2015 deve ser descartada da estratégia consolidada;
Quando da utilização do método relativo, deverá ser adotado o ponto P 0 mais próximo do centro da área estudada, como aproximação primária para seu baricentro, haja visto que esta consideração demonstrase suficientemente eficaz para o princípio que ora se propõe e que outras configurações testadas não apresentaram ganho significativo;
Quando da obtenção de extratos dos MGGs serão utilizados os modelos EGM2008, EIGEN-6C4, GOCO05C e XGM2016, segundo graus de desenvolvimento 720 e 2190 - exceção feita ao MGG XGM2016, para o qual será utilizado seu grau máximo 719 - em virtude destes originarem funcionais do geopotencial que melhor representam a altitude normal-geoidal;
Ainda quando da obtenção de extratos dos MGGs, serão consideradas as funcionais anomalia de altitude e altitude geoidal, vislumbrando a modelagem da altitude normal-geoidal, uma vez que não houve comportamento padronizado para os resultados neste aspecto;
A escolha da configuração ótima se dará para o MGG, o grau de desenvolvimento e a funcional que minimizarem o fator θ m para o conjunto de pontos estudado;
Após a determinação das altitudes normais-ortométricas em área desejada, deve ser realizada uma validação dos resultados em uma área desejada controlável, com precípua eliminação de outliers;
Avanços na determinação de altitudes normais-ortométricas na área de estudo
Analogamente ao desenvolvido na área-teste, realizou-se a busca por uma configuração ótima na área de estudo, a qual foi identificada como o GGM XGM2016, desenvolvido até grau 719 e segundo a funcional anomalia de altitude; segundo esta configuração, obteve-se discrepância média θ m = 0,2160 m = 21,60 cm. A Figura 5 apresenta gráfico similar àquele disposto na Figura 4, para esta área.

Fonte: Nicacio, 2017
Figura 5 Gráfico de diferenças médias, em metros, para método absoluto e relativo por grau de desenvolvimento dos modelos na área de estudo.
Para a área de estudo pode-se, também, elaborar a Tabela 3, a qual demonstra os ganhos impostos pela utilização da metodologia alternativa em comparação a uma metodologia tradicional, analogamente ao realizado na Tabela 2. Novamente, estas estimativas finais foram realizadas após uma fase de identificação e eliminação de outliers, baseada em um critério de até um desvio-padrão de diferença em relação à média do conjunto de pontos. Das 136 estações GNSS/RN utilizadas para este fim, 22 foram eliminadas com este critério, indicando possíveis problemas em suas determinações altimétricas originais.
Tabela 3 Comparativo entre metodologia proposta e metodologia tradicional na área de estudo
| Metodologia alternativa | Metodologia tradicional | |||||
| θ (m) | σθ 2 (m²) | σθ (m) | θ (m) | σθ 2 (m²) | σθ (m) | |
| Máxima | 0,3665 | 0,0112 | 0,1057 | 0,9029 | 0,0468 | 0,2164 |
| Média | 0,1387 | 0,3628 | ||||
| Mínima | 0,0006 | 0,0244 | ||||
Fonte: Nicacio (2017).
Sendo assim, novamente atesta-se que os ganhos da aplicação da metodologia ora proposta são reais e de grande significância para a aplicação da estratégia alternativa. Estes resultados confirmam a superioridade da metodologia e da estratégia consolidada utilizadas, proporcionando ganhos superiores a 20 centímetros para determinações altimétricas na complexa Região Amazônica.
Estimativa do off-set entre DVB-I e DVB-S
Ao final dos trabalhos, verificou-se ainda a possibilidade de realizar uma nova estimativa da separação vertical (off-set) entre os data verticais brasileiros - DVB-I, em Imbituta-SC, e DVB-S, em Santana-AP - com base no uso da metodologia proposta. Aprofundamentos sobre esta abordagem podem ser encontrados no trabalho original; entretanto, os resultados encontrados mostram-se deveras consistentes com aqueles já obtidos anteriormente, conforme apontado na Tabela 4. As principais discrepâncias são devidas às imprecisões dos dados de entrada para a metodologia, bem como a diferentes abordagens para solução do problema.
Tabela 4 Atualização de autores e valores determinados de off-set entre data verticais
| Autor | Off-set (m) |
| Nicacio (2017) | 1,320 ± 0,07 m |
| De freitas et al. (2016) | 1,416 ± 0,12 m |
| Moreira (2015) | 1,300 ± 0,11 m |
| Castro e De Freitas (2014) | 1,301 a 1,420 m |
| Castro (2011) | 1,320 m ou 1,430 m |
Fonte: Nicacio (2017).
Conclusões e Contribuições do Trabalho
Foi desenvolvida uma ferramenta, em duas versões conforme necessidade, para rápida obtenção de extratos de MGGs ponto-a-ponto com acesso direto ao serviço web do ICGEM: o SPGG (Nicacio, 2016). Com seu uso, foram obtidos dados necessários para este e para outros trabalhos, de tal maneira que o usuário regular não necessite realizar manipulações matemáticas complexas com os coeficientes do desenvolvimento dos modelos em harmônicos esféricos, tampouco dependa da interação repetitiva com o referido serviço. Esta ferramenta encontra-se disponível para download no endereço da referência e pode ser livremente utilizada pela comunidade, principalmente para o público que necessita trabalhar com extratos de modelos globais e não deseja realizar uma manipulação direta de seus coeficientes.
Foi analisado o desempenho do uso do método relativo ante ao método absoluto para predições altimétricas baseadas no uso de MGGs e de altitudes elipsoidais. Esta pode ser considerada a principal contribuição do presente trabalho, tendo em vista que os resultados das análises a ela referentes indicam que a maneira ideal de lidar com os MGGs e suas funcionais é, de fato, com o uso do método relativo, tomadas precauções quanto ao pleno alinhamento com conceitos físicos atinentes. Foi analisado o desempenho de expoentes MGGs combinados da atualidade em porções específicas do território nacional - a saber, estado do Paraná e Amazônia Legal Brasileira - quanto à adequação para modelagem da altitude normal-geoidal. Esta contribuição fomentou ainda a confecção de artigo acadêmico com abrangência do território nacional em completude.
Foram desenvolvidas especificações e orientações quanto à metodologia alternativa para predição de altitudes normais-ortométricas com base em MGGs e suas funcionais, observações GNSS e uso do método relativo, com vistas a densificar a informação altimétrica na região de carência na Amazônia Legal Brasileira. Estas orientações podem ser expandidas para emprego em todo o território nacional conforme necessidade, desde que conservadas as precauções imperativas descritas ao longo do trabalho. Os estudos demonstraram uma necessidade de revisão em normativas existentes que apontam para o uso do método absoluto como alternativa para o nivelamento geométrico quando da predição de altitudes normais-ortométricas, como aquelas preconizadas por Aneel (2009, p. 23) para pequenas centrais hidrelétricas, e a implementação de normatização para uso dos MGGs.
Por fim, proveu-se uma nova estimativa para o afastamento entre os data verticais brasileiros, baseado no emprego da metodologia desenvolvida. Seu resultado coerente com as demais estimativas existentes confirmam a correção da metodologia desenvolvida e dos processos empregados, somando-se a estes resultados anteriores como possíveis valores para o off-set em questão.











 nueva página del texto (beta)
nueva página del texto (beta)




