1. Introducción
Los modelos digitales de elevaciones del terreno (MDE) son datos topográficos que siguiendo un modelo (p.ej. curvas de nivel, nubes de puntos, mallas, redes de triángulos, etc.) representan digitalmente las elevaciones (cotas o altimetría) del terreno desnudo. Los MDE son datos de gran relevancia y se han incluido como un tema de INSPIRE y de NNUU. Los MDE tienen aplicación en numerosas ramas de la ciencia y de la ingeniería y se utilizan principalmente para el cálculo de la altura, la pendiente, orientación y delimitación de cuencas (Ariza-López y col., 2018).
La calidad de los MDE suele entenderse en el ámbito geomático como la exactitud posicional altimétrica de los datos. Son muy numerosas las aproximaciones y métodos desarrollados para evaluar esta exactitud posicional (Mesa-Mingorance & Ariza-López, 2020). La mejor forma de evaluar o controlar la exactitud posicional es aplicando métodos estandarizados. Una guía actual de los más destacados se presenta en Ariza-López y col. (2018). Entre otros muchos, algunos de estos métodos son el NMAS (USBB, 1947), el NSSDA (FGDC, 1998), el EMAS (ASCE, 1983), las propuestas de la ASPRS (ASPRS, 1990, 2015) y la propuesta de EuroSDR basada en medidas con un enfoque paramétrico (Höhle & Potuckova, 2011). Ariza-López y Atkinson-Gordo (2008) indican que muchos de los métodos existentes para la evaluación de la exactitud posicional se basan en el supuesto de normalidad de los errores. Sin embargo, muchos trabajos (Zandbergen, 2008, 2011; Maune, 2007) indican que los errores de posición no se distribuyen normalmente.
La distribución normal es una distribución adecuada para representar variables aleatorias de valor real. Por lo tanto, plenamente adecuada para describir el error altimétrico. Sin embargo, la abundancia de referencias que indican la no normalidad de los datos de error posicional altimétrico conduce a tres preguntas importantes: (1) ¿por qué estos errores pueden no estar distribuidos normalmente?, (2) ¿cómo afecta la falta de normalidad a los métodos basados en el supuesto de datos distribuidos normalmente? y finalmente, (3) ¿cómo podemos trabajar con estos datos?
Para la primera pregunta, y desde un punto de vista general, se pueden considerar seis causas principales de la no normalidad en un conjunto de errores posicionales: (i) la presencia de demasiados valores extremos (es decir, valores atípicos), (ii) la superposición de dos o más procesos (p.ej. de captura, de evaluación, etc.), (iii) insuficiente discriminación de datos (por ejemplo, errores de redondeo, mala resolución), (iv) la eliminación de datos de la muestra, (v) la distribución de valores cercanos a cero o a su límite natural, y (vi) datos que siguen una distribución diferente (por ejemplo, Weibull, Gamma, etc.). Además, para mayor complejidad, algunas de estas causas pueden aparecer juntas.
Con respecto a la segunda pregunta, y trabajando con métodos basados en el supuesto de normalidad de los datos, la no normalidad de éstos puede tener varias consecuencias dependiendo del grado de no normalidad y la robustez del método aplicado. En este caso, la no normalidad viola un supuesto básico del método, y esta violación es importante desde una perspectiva estricta.
Finalmente, para responder a la tercera pregunta, hasta la fecha se han considerado dos alternativas: (a) los datos no se distribuyen normalmente, pero siguen alguna otra función de distribución paramétrica (por ejemplo, Weibull, Gamma, etc.), (b) los datos no siguen una distribución paramétrica. En este trabajo se explora una tercera vía que consiste en suponer que los datos de error altimétrico realmente no proceden de una única distribución y que, por el contrario, son el resultado de la mezcla o mixtura de varias distribuciones. Esta tercera vía es muy potente, e interesante, pues consiste en descomponer la función de densidad observada en una composición de un cierto número de funciones normales tal que la aproximen adecuadamente, es decir, se trabaja con una herramienta equivalente a lo que en análisis de señales consiste en descomponer una señal por medio de series de funciones seno/coseno (transformada de Fourier).
La idea subyacente es que la variable observada realmente procede de una mezcla de datos de distribuciones que siguen un mismo modelo (el normal), pero con diferentes parámetros. De esta manera, la probabilidad de un valor observado procede de la mezcla de las probabilidades de que proceda de cada una de las distribuciones que componen la mixtura. Los primeros trabajos se remontan a 1894, cuando Pearson trabajó con la mezcla de dos distribuciones normales con la misma varianza y ha sido desarrollada por múltiples investigadores (una revisión detallada puede verse en McLachlan-Peel, 2000; McLachlan et al., 2019, o Huang et al., 2017 y algunos ejemplos de aplicaciones recientes de mixturas en diferentes campos pueden verse en Pan et al., 2020; Sallay et al., 2020; Zhao et al., 2021 o Li et al., 2021).
El objetivo de este artículo es proponer un método estadístico nuevo y general para la evaluación de la exactitud posicional altimétrica que se pueda aplicar a cualquier tipo de datos de error procedentes de MDE.
Este documento se organiza de la siguiente manera. La sección 2, presenta una aproximación conceptual básica a la mixtura de distribuciones normales. En la sección 3, se propone un método de aplicación y en la sección 4 se aplica paso a paso, el método propuesto al caso de datos procedentes de dos productos MDE con pasos de malla de 2x2 y 5x5. La sección 5, presenta la discusión y finalmente, se incluyen unas conclusiones generales.
2. Mixtura de distribuciones normales
Una causa frecuente de no normalidad es la existencia de subgrupos dentro de la población que no son previamente conocidos, de modo que, aunque cada uno de esos subgrupos sigan una distribución normal diferente, la combinación de todos ellos producen un resultado que no se distribuye normalmente. Una manera de detectar estos subgrupos es tratar de determinar, por medio de sus parámetros (media y desviación), cuáles son las distribuciones normales que se mezclan en la composición de la distribución original.
Una técnica para detectar y obtener estas componentes consiste en el estudio de las mixturas finitas de distribuciones normales. Desde un punto de vista teórico, supongamos que el vector X1, …, Xn es una muestra aleatoria simple procedente de una mezcla de k > 1 distribuciones arbitrarias de probabilidad, cada una de ellas con una función de densidad фj. Entonces, la función de densidad de cada Xi viene expresada por (Ecuación 1):
en dónde θ ϵ Θ = (π, Φ) = (π1, …, π k, Φ1, …, Φk) es el vector de parámetros de modo que πj es la probabilidad en la que la densidad j aparece en la mezcla, en donde π1 + ... + πk = 1 y todos mayores de 0. Además, suponemos que cada Φj procede de alguna familia de distribuciones de probabilidad absolutamente continuas, F. Vamos a considerar el caso en que F es la familia de distribuciones normales univariantes, es decir, F={Φ(∙ | μ, σ)} es el conjunto de funciones de densidad N (μ, σ), (μ, σ) ϵ R × R+, por lo que el vector de parámetros que hay que estimar, Θ, se reduce a Θ = (π1, … , πk , (μ1, σ1), … , (μk , σk)).
Por tanto, para determinar las distribuciones que componen la mezcla se requiere estimar los 3k parámetros del vector Θ. Para ello se puede utilizar el algoritmo EM (algoritmo de maximización de expectativas) desarrollado por Dempster et al. (1977), que ofrece una solución iterativa del cálculo de estimaciones de máxima verosimilitud (ML) en problemas con valores faltantes. Su uso se ha extendido no solo para datos evidentemente incompletos (datos faltantes, distribuciones truncadas, observaciones censuradas o agrupadas), sino también modelos estadísticos donde la falta de los datos no es tan evidente (McLachlan-Krishnan, 2008), como ocurre con distribuciones que surgen como mixturas (Karlis, 2005), dado que pueden verse como un caso particular de estimación ML en donde las observaciones pueden considerarse como datos incompletos. En este caso vamos a utilizar el algoritmo EM implementado en el paquete mixtools de R (Benaglia et al., 2009; R Core Team, 2020), que produce una estimación del vector de parámetros Θ̂ en función del número de distribuciones mixtantes consideradas.
Una vez estimados los parámetros y, aplicando el teorema de Bayes, se puede proceder a realizar un agrupamiento probabilístico que asigna cada punto del conjunto original mezclado a aquella distribución normal a la que es más probable que pertenezca, según las probabilidades a posteriori. Así (Ecuación 2):
en donde g es el número de distribuciones que componen la mixtura y π̂ij es la probabilidad a posteriori de que el punto xi pertenezca a la población con función de densidad fi. De esta manera, dada una observación xj, ésta se asigna a aquella distribución normal para la que la citada probabilidad sea máxima.
3. Método de aplicación
Tomando como herramienta central el análisis estadístico de mixturas finita de distribuciones, en este apartado se propone un método para aplicarlo al caso de las discrepancias altimétricas entre MDE. El método es el siguiente:
Decisión sobre población o muestra. En primer lugar, se debe decidir si trabajar con el total de la población de discrepancias o con una muestra. Esto vendrá determinado por las condiciones y necesidades específicas de cada caso, y no condiciona los pasos subsiguientes.
Aproximación a los datos. Consiste en un análisis estadístico-descriptivo para conocer mejor los datos con los que se trabaja. Se debe incluir un análisis de la normalidad puesto que, si los datos fueran normales, no tendría sentido proceder a la descomposición como mixtura. Siendo los datos no normales, se requiere especialmente un estudio detallado del histograma en la línea de buscar sus componentes de una manera visual (véase 4.3).
Selección del modelo. Consiste en determinar el número de distribuciones normales que se considera se mezclan dando el modelo general. Esta decisión se basa en el estudio del histograma indicado en el punto anterior.
Obtención de los parámetros por el algoritmo EM y análisis de los resultados. Se procederá a ejecutar el proceso de estimación EM y, como resultado, se obtendrán los parámetros de la cada una de las normales mixtantes y su peso en la mezcla.
Expansión del ajuste a la población. Si se ha trabajado con la población este punto no tiene necesidad. En el caso de trabajar con muestras, se deberá aplicar el modelo a todas y cada una de las discrepancias que conforman la población.
Análisis de los resultados. Los resultados se analizarán en un marco estadístico y espacial, en el contexto de la zona de trabajo y los medios que originaron los datos con los que se ha trabajado.
4. Aplicación a un caso real
Una vez presentados los principios estadísticos del análisis de mixturas y el método propuesto, en este apartado nos focalizaremos en aplicar ambos sobre un caso real. Primeramente, se presentan los datos y posteriormente cada una de las fases del método expuesto en la sección 3.
4.1 El conjunto de datos y su descripción numérica
Se va a trabajar con las discrepancias altimétricas entre dos conjuntos de datos MDE que se considerarán como errores altimétricos. Los MDE corresponden a la zona de Allo (Navarra, España, hoja 0172 del Mapa topográfico nacional), y son:
MDE02. Modelo digital de elevaciones a resolución de 2x2 m, generado en 2017 y procedente del levantamiento LiDAR del proyecto PNOA (https://pnoa.ign.es/) (https://pnoa.ign.es/estado-del-proyecto-lidar/segunda-cobertura). Este conjunto de datos será considerado como referencia en este trabajo.
MDE05. Modelo digital de elevaciones a resolución de 5x5 m, generado en 2012 y procedente del levantamiento LiDAR del proyecto PNOA (https://pnoa.ign.es/estado-del-proyecto-lidar/primera-cobertura). Este conjunto de datos será considerado como producto a evaluar.
Ambos conjuntos de datos proceden del Instituto Geográfico Nacional de España (https://www.ign.es) y están a libre disposición en el centro de descargas. La Figura 1 presenta una visión general de la zona de trabajo. La zona de trabajo posee una topografía variada (valles, torrenteras, zonas onduladas, etc.), que ofrece diversidad de situaciones.
4.2. Decisión sobre población o muestra
En este caso se ha decidido trabajar con una muestra para la determinación del número de normales y la estimación de los parámetros. La selección de una u otra perspectiva se relaciona con diferentes factores, entre ellos, capacidad de cálculo, aplicabilidad de los resultados, etc. En este caso la muestra se compone de 338 635 puntos agrupados en 59 polígonos de los que se han extraído las altitudes en MDE05 y MDE02.
4.3. Aproximación a los datos
Los datos a analizar se corresponden con las discrepancias entre MDE05 y MDE02, tomando como referencia MDE02 dado que procede de una fuente de más exactitud. Un análisis descriptivo de las discrepancias altimétricas que conforman la muestra aparece en la Tabla 1.
Tabla 1 Análisis descriptivo de los datos de la muestra
| Media | Mediana | Desv. típica | Mín. | Q1 | Q3 | Máx. |
| -0.0175 | -0.0605 | 0.2800 | -1.6284 | -0.1257 | 0.0356 | 3.0940 |
De aquí se desprende que los datos aparecen muy levemente sesgados a la izquierda en media y con una desviación típica relativamente elevada. Además, dado que la mediana es menor que la media, los datos presentan cierta asimetría a la derecha, lo que se corrobora al ver los valores mínimo y máximo.
Para analizar la normalidad, la Figura 2 muestra el gráfico en “papel probabilístico normal”, de las discrepancias o errores posicionales verticales. En él se puede observar cómo la curva presenta una forma sinuosa y se separa mucho de la línea recta dibujada y que se corresponde con una normal de media y desviación correspondientes a los valores presentados en la Tabla 1. En este tipo de gráfico, cuanto más se separa la curva de la recta, tanta mayor es la falta de normalidad de los datos. Esta figura evidencia que no se podría aplicar un método de evaluación de la exactitud posicional basado en la normalidad, si bien podrían aplicarse métodos basados en proporciones como el propuesto por Ariza-López y Rodríguez-Avi (2019).
Una parte importante del método gráfico para determinar el número de distribuciones es el análisis del histograma. Para ello, la Figura 3 muestra el histograma general y completo, y en la Figura 4, dos niveles de zoom de mayor detalle. En la Figura 3 se observan varios picos, modas locales y colas a izquierda y derecha. En la Figura 4, enfocada en los valores centrales, se obtiene más detalle de lo que ocurre en la parte donde se acumulan más casos y donde se evidencian, aún más, la superposición de distribuciones. Si comparamos la forma de ésta con el histograma de una distribución normal, podemos observar la presencia de diferentes modas locales y engrosamientos de los laterales. Esto, junto a la sinuosidad presente en la Figura 2, invita a considerar que los datos pueden ser explicados como mixtura de diferentes distribuciones normales.
4.4. Selección del modelo
Este paso consiste en determinar el número de distribuciones normales que componen la mezcla que mejor se ajusta a los datos (histograma general). Para ello proponemos optar por un acercamiento gráfico a partir de lo mostrado en las figuras anteriores. De esta forma, la presencia de modas y sus posibles colas, nos sugieren una posible mezcla de 6 distribuciones normales diferentes. Indudablemente, este proceso puede ser iterativo (prueba y error) y abarcar los pasos subsiguientes que sea menester. En esta decisión jugará un papel importante la experiencia que se vaya adquiriendo en este tipo de análisis.
4.5. Ajuste por medio de EM y análisis de los resultados
Una vez seleccionado el número de normales, se debe proceder al ajuste del modelo y al análisis de los resultados. El proceso de ajuste se realiza con la función normalmixEM del paquete mixtools de R, como se ha comentado anteriormente. Tras alimentar la función con los datos y tomar la decisión de no introducir probabilidades a priori para las categorías consideradas, la herramienta ofrece como resultado un total de 18 parámetros, consistentes en los 6 pares de media y desviación típica de cada distribución normal, y el vector de proporciones de datos en cada distribución normal. Los resultados se muestran en la Tabla 2, en donde la media y la desviación típica vienen medidos en metros.
Tabla 2 Vector de parámetros estimados
| Parámetro | Grupo 1 | Grupo 2 | Grupo 3 | Grupo 4 | Grupo 5 | Grupo 6 |
| μ | 0.326 | -0.102 | -0.255 | -0.011 | -0.061 | -0.084 |
| σ | 0.885 | 0.036 | 0.084 | 0.033 | 0.060 | 0.309 |
| π | 4.70% | 34.18% | 9.05% | 17.13% | 9.27% | 25.76% |
De la Tabla 2 se deduce que las 6 distribuciones estimadas son N1 (0.326;0.885), que representa al 4.60% de los datos; N2(-0.102;0.036), que representa al 34.18% de los datos; N3(-0.255;0.084), que representa al 9.05% de los datos; N4(-0.011;0.033), que representa al 17.13% de los datos; N5(-0.061;0.060), que representa al 9.27% de los datos y N6(-0.084;0.309), que representa al 25.76% restante de los datos. Es decir, hay un conjunto pequeño de datos que se encuentran sesgados a la derecha y muy dispersos, y tan sólo un 17% de datos corresponden a errores con media prácticamente 0. Es de destacar también altos valores de las desviaciones típicas y que los grupos con mayores probabilidades de pertenencia están sesgados a la izquierda y a la derecha, éste último con una desviación típica elevada. La Figura 5 representa gráficamente el ajuste de las 6 distribuciones normales y el ajuste a la verdadera densidad observada, que es la línea punteada.
4.6. Expansión del ajuste a la población
Una vez obtenidas las distribuciones normales el paso siguiente consiste en asignar cada valor de la población a la distribución normal a la que es más probable que pertenezca. Para ello se parte de la matriz que contiene las probabilidades a posteriori de pertenencia a grupos, obtenida a partir de (2) y se considera que un elemento pertenece a la distribución normal en la que esa probabilidad de pertenencia sea máxima. Un ejemplo de este procedimiento se muestra en la Tabla 3 donde se presentan tres puntos del MDE identificados, por lo que se conoce su posición, y el valor de discrepancia entre MDE05 y MDE02 y las probabilidades de pertenencia a cada una de las normales. De modo que el primer punto se asigna a la distribución 6, el segundo a la distribución 3, el tercero a la distribución 1 y así se haría sucesivamente con todos los puntos de la población.
Tabla 3 Matriz de probabilidades a posteriori (ejemplo)
| ID-Punto | Discrepancia | N1 | N2 | N3 | N4 | N5 | N6 |
| 141943 | -0.507 | 0.186 | 0.000 | 0.068 | 0.000 | 0.000 | 0.746 |
| 123661 | -0.220 | 0.027 | 0.030 | 0.620 | 0.000 | 0.000 | 0.323 |
| 95477 | 1.244 | 0.977 | 0.000 | 0.000 | 0.000 | 0.000 | 0.023 |
| 75233 | 0.672 | 0.262 | 0.000 | 0.000 | 0.000 | 0.000 | 0.738 |
De la forma indicada en el párrafo anterior, se ha calculado la probabilidad de pertenencia de cada una de las posiciones del MDE para cada una de las normales consideradas. Esto es lo que se presenta en la Figura 6. En cada sub-figura se presenta el valor de la probabilidad asignada en una escala que va del blanco (cero), hasta el rojo (1), pasando por una gama de colores amarillos y naranjas. Mientras que la Figura 7 presenta la probabilidad máxima de pertenencia. Como se puede observar en la Figura 6, para el caso de N1 abundan mucho el blanco, lo que quiere decir que hay mucho espacio con probabilidad de pertenencia baja a esta normal, la cual es muy selectiva, pues como vemos los valores rojos se concentran en algunas zonas aisladas. No ocurre lo mismo con N2, en este caso hay zonas de valor nulo, pero existe un marcado tono rojizo generalizado que indica alta probabilidad de pertenencia. Los casos de N3, N4 y N5 son casos en los que hay ciertas zonas en blanco, pero el resto del espacio tiene una probabilidad de pertenencia media. En el caso de N6 se observa que se cubre casi todo el espacio con probabilidades medias y altas. En La Figura 7 se muestra la probabilidad que finalmente se asigna a cada posición, que se corresponde con el max (P (N1), P (N2), P (N3), P (N4), P (N5), P (N6)), por lo que los tonos rojizos están mucho más subidos.

Figura 6 Mapas de probabilidad de pertenencia a cada una de las 6 normales consideradas (N1, N2… N6) ordenadas de izquierda a derecha y de arriba a abajo.
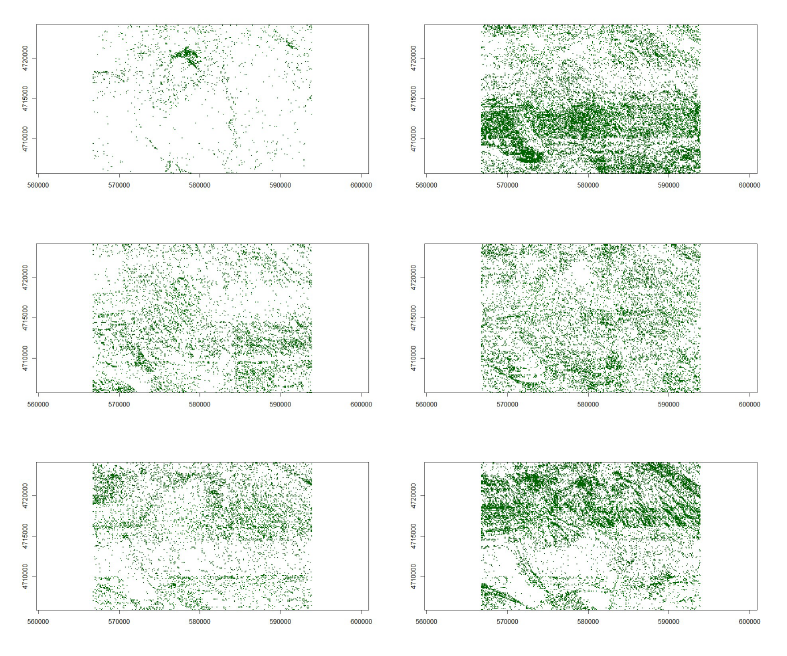
En cuanto a la asignación a cada una de las categorías definidas por cada una de las normales, la Figura 8 presenta la asignación de la clase que ofrece el valor a la función MAX(P(N1), P(N2), P(N3), P(N4), P(N5), P(N6)). En cada sub-figura se presenta la asignación espacial a esa categoría (verde= asignado, blanco= no asignado). Si bien, salvo la asignación a la N1, que muestra una distribución espacial muy restringida, el resto de asignaciones presenta una amplia cobertura de la zona de trabajo, en estas figuras se pueden observar patrones de asignación que poseen cierta relación con las características orográficas del terreno (p.ej. N2 en la zona sur y N6 en la zona norte). Finalmente, la Figura 9 presenta la visión conjunta de todas las asignaciones.
4.7. Análisis de los resultados
En este trabajo se propone la posibilidad de utilizar el método de mixturas finitas de distribuciones para modelizar valores procedentes del estudio de errores en altimetría, para lo cual se ha optado por un método gráfico para determinar el tamaño de la mezcla. En este sentido, en el ejemplo presentado, para mayor simpleza, se ha considerado sólo el caso de 6 normales provenientes de un análisis visual del histograma. Desde un punto de vista estadístico el ajuste a un modelo de 6 normales podría ser discutido en cuanto a su bondad: por qué no 5 normales, o por qué no 7 u 8 normales. Este proceso puede ser más robusto desde el punto de vista estadístico si se ensayara un conjunto de opciones (p.ej. de 2 a 10 mixturas) y se analizara la bondad de cada uno de los resultados por medio de índices como criterio de Información de Akaike (AIC) o el criterio de información bayesiano (BIC) entre otros, y que son utilizados en el ajuste de modelos (Cameron-Trivedi, 2013). Este análisis no es costoso más allá del tiempo de cálculo que requiere el EM para una gran cantidad de datos.
En relación a los resultados obtenidos, se puede analizar la tipología de éstos y, para el caso bajo estudio, la adecuación a la realidad del terreno. Desde el primer punto de vista, consideramos que los resultados son muy valiosos pues ofrecen la oportunidad de seguir trabajando con el paramétrico de la normal, pero de una manera mucho más cercana a la realidad. Para ello vamos a calcular la probabilidad teórica de diversos valores de la variable y comprobar cuál es su correspondiente contrapartida en los datos observados.
Para calcular una probabilidad teórica a partir del modelo de mixturas, se puede utilizar el Teorema de la Probabilidad Total, de manera que la probabilidad de un punto es (Ecuación 3):
es decir, la probabilidad que se obtiene en cada una de las 6 normales multiplicada por la probabilidad a priori de pertenencia, πi.
La Tabla 4 muestra la comparación entre la media y los cuartiles obtenida desde del modelo poblacional y la estimada a partir de la muestra. Para comparar los resultados, la última fila muestra los valores que se obtendrían si la población siguiese una única distribución normal N (-0.0175, 0.2800), con los parámetros estimados a partir de la muestra.
Tabla 4 Comparación entre el modelo y la muestra (I)
| Parámetro | Media | Mediana | Q1 | Q3 |
| Valor en la Muestra | -0.0175 | -0.0605 | -0.1257 | 0.0356 |
| Valor en el Modelo Mixtante | -0.0174 | -0.0603 | -0.1261 | 0.0353 |
| Valor en la N (-0.0175,0.2800) | -0.0175 | -0.0175 | 0.0474 | 0.1713 |
Del mismo modo, la Tabla 5 muestra la probabilidad de los valores indicados a partir del modelo obtenido por la mixtura y por la distribución N(-0.0175, 0.2800), con los parámetros estimados a partir de la muestra (dos últimas filas).
Tabla 5 Comparación entre el modelo y la muestra (II)
| Valor | ≤0m | <-1m | >0.50 m | ≥1m |
| Proporción en la muestra | 0.6716 | 0.0027 | 0.0393 | 0.0099 |
| Probabilidad en el Modelo mixtante | 0.6706 | 0.0031 | 0.0423 | 0.0106 |
| Probabilidad en la N(-0.0175,0.2800) | 0.5249 | 0.0002 | 0.0323 | 0.0001 |
En ambas tablas se observa como el modelo teórico obtenido a partir de la mixtura de las 6 normales proporciona una buena aproximación a los datos muestrales. Una comprobación gráfica del ajuste se muestra en la Figura 10, en donde la línea representa la densidad teórica superpuesta al histograma de la Figura 1, y los valores de la variable están medidos en metros.
La Figura 11 muestra una ampliación detallada para los valores centrales, entre -1 y 1 (izquierda) y entre -0.5 y 0.5 (derecha) para apreciar con detalle cómo el modelo teórico se ajusta a los datos muestrales, incluso en las modas locales.
Del mismo modo, la Figura 12 muestra el gráfico de cuantiles (QQ-plot), en donde se observa que la representación gráfica es prácticamente una línea recta diagonal, lo que demuestra que el ajuste es muy bueno.
Esto se reafirma al calcular la distancia de Kolmogorov-Smirnov entre ambas funciones de distribución, en dónde el resultado es 0.00030.
Adicionalmente la Figura 13 muestra la comparación entre las funciones de distribución del modelo y empírica en el rango de error entre -0.5 m y 0.5 m, en la que se observa como ambas líneas se superponen prácticamente.

Figura 13 Comparación de las Funciones de distribución teórica y empírica (rango entre -0.5 m y 0.5 m) y cuantiles del 90% y del 95%.
Esta información sobre el modelo puede utilizarse para determinar cuantiles en el modelo teórico y que puedan ser empleado en otros procedimientos. De hecho, en esa misma Figura 13, se muestra el valor de los cuantiles para las probabilidades acumuladas del 90% (0.252 m) y del 95% (0.454 m).
Una vez obtenido el modelo probabilístico teórico que siguen los datos observados se puede utilizar para profundizar en el conocimiento de éstos, utilizando para ello cualquier información adicional disponible. En este caso, dado que para cada error disponemos de las coordenadas de los puntos en los que se mide, se puede utilizar para obtener una distribución espacial de los errores en función del grupo al que es asignado. Esta espacialización permite realizar análisis, en mayor o menor profundidad, orientados a la interpretación de qué representa cada una de las componentes de la mixtura. Por ejemplo, en la Figura 9 se observa que las N2 y N6 son las más abundantes, presentando grandes manchas y con clara distinción S y N respectivamente. Por su parte, la N1 está muy focalizada y centrada en pocas posiciones. Las N3 y N4 se encuentran muy repartidas y podríamos decir que “pixeladas”, la primera tanto en el N como en el S, pero con más abundancia en el S. La N4 más pixelada en el S y con mayor grado de agrupación en el N, y siempre espacialmente cercana a la N6. Estos análisis podrían relacionarse con la cubierta y uso del terreno. Por ejemplo, la N1 parece relacionada con terrenos suaves y alomados y la N6 con terrenos más abruptos. Este análisis se puede vincularse con la pendiente y orientación del terreno, técnicas de captura, etc., con vistas a conocer mejor la composición de distribuciones de error que aparecen en un producto como es un MDE.
5. Discusión
La hipótesis de que los errores de medida siguen una distribución normal está en la base teórica de la misma distribución. De hecho, Gauss la obtuvo asumiendo errores de medida independientes. El hecho que unos residuos se distribuyan normalmente, además implica que su causa es el puro azar, sin que haya otras causas que afecten en el resultado. Por ese motivo es la hipótesis usual en la mayoría de técnicas asociadas al control de calidad. Sin embargo, en múltiples ocasiones si se mezclan errores normalmente distribuidos, pero con distintos parámetros provoca que el resultado obtenido al mezclarlos no sigue estrictamente un modelo normal.
En este trabajo se ha presentado una aplicación novedosa en el campo de los MDE de una técnica de mixturas finitas para descomponer los datos de error cuando proceden de distintas normales. De esta manera, y a partir de una muestra, se puede inferir el modelo poblacional de errores, lo que permite obtener unos valores y límites más precisos, al poder estimar probabilidades asociadas a los mismos. La aplicación al caso del error altimético propio de los MDE es sólo una de las muchas aplicaciones que se podrían pensar en el campo de la geomática. Como técnica estadística su aplicación no conlleva más limitaciones que las propias de su conceptualización y que se establecen por medio de las hipótesis que se asumen. En el caso del error el uso de mixturas normales puede ser adecuado, aunque este tipo de mixturas finitas también puede plantearse con otras distribuciones, bien continuas (Log-normal, Gamma, Weibull) como discretas. En cualquier caso, entendemos que, al igual que una señal puede ser descompuesta por el análisis de Fourier en una composición de funciones más sencillas, en el caso estadístico esto también es válido respecto al uso de la mixtura de normales. Comparada la técnica de mixtura con otras técnicas estadísticas (p.ej. el análisis cluster), esta técnica presenta la ventaja de definir claramente el modelo paramétrico de todas y cada una de las agrupaciones que se generan.
El método de trabajo propuesto posee seis pasos definidos según una secuencia lógica y racional, por lo que es común a otros muchos procesos de análisis estadístico, y se puede considerar como un método estándar. En este proceso la manera en que se realice la selección del modelo queda libre. Así, si bien la terminación del número de mixturas se ha planteado en este trabajo de manera visual, también podría realizarse de manera automática. Para ello se podría establecer un rango predefinido de análisis y utilizar criterios de información como el AIC y BIC ya indicados anteriormente, para la selección final del modelo. En cualquier caso, consideramos que la prueba y error basada en la realimentación con el análisis de los resultados respecto a la realidad del terreno y de la captura que generó los conjuntos de datos que se comparan, será la mejor manera de determinar el número de normales a considerar en la mezcla.
Consideramos, que los resultados que se obtienen son muy interesantes desde el punto de vista de los trabajos estadísticos con toda la población. Además, los ejemplos numéricos mostrados en 4.7 no son alcanzables con otros métodos de manera directa. Esta capacidad de trabajar con un modelo probabilístico paramétrico para toda la población de discrepancias es una herramienta potente, y abre las puertas a nuevas formas de aplicación de los estándares de control posicional que se venían aplicando. La capacidad de espacialización es otro aspecto reseñable, y sólo queda limitado por el conocimiento de las discrepancias o errores.
6. Conclusiones
Se ha presentado la primera aplicación de las técnicas de análisis de mixtura al caso de las discrepancias altimétricas en MDE. La herramienta conceptual estadística está madura y su aplicación queda facilitada por medio de las herramientas de software existentes. En este trabajo se ha propuesto un método para este tipo de análisis, y se ha desarrollado una aplicación práctica que evidencia la manera de realizar esta aplicación, así como los resultados que se obtienen. La aplicación al caso de discrepancias altimétricas es relativamente directa.
Consideramos que, mutatis mutandis, esta nueva técnica de análisis de las discrepancias altimétricas puede permitir aplicar los métodos de evaluación de la calidad posicional convencionales, a una familia de normales que se mixturan, lo cual abre una línea que extiende sus posibilidades soslayando las limitaciones de la no normalidad que se han apuntado en números estudios del error altimétrico.











 nueva página del texto (beta)
nueva página del texto (beta)