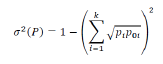nueva página del texto (beta)
Español (pdf)
Artículo en XML
Referencias del artículo
Traducción automática
Enviar artículo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
1. Introducción
Un Modelo Digital de Elevaciones (MDE) es un conjunto de datos, en soporte y modelo digital, que representa las elevaciones de la superficie desnuda del terreno (sin vegetación ni características artificiales). Los MDE permiten analizar las características morfológicas del relieve, su topografía (p.ej. colinas, crestas, valles, ríos, etc.), y se pueden derivar una gran cantidad de parámetros (por ejemplo, pendiente, orientación, curvatura, etc.).
Los MDE son productos de datos con aplicaciones en un amplio conjunto de disciplinas como Ingeniería Civil (Stroeven et al., 2015), Hidrología (Saksena y Merwade, 2015), Geomorfología (Gómez et al., 2015), Agricultura (Rekha et al., 2015), Silvicultura (Juel et al., 2015), etc. Dos usos principales de los MDE son el cálculo de la pendiente y la orientación (Mesa-Mingorance y Ariza-López, 2020; Ariza-López et al., 2018). Utilizando algoritmos relativamente simples, los modelos digitales de pendiente y orientación se derivan de los MDE. El cálculo de estos parámetros se basa en un análisis local de la derivada de elevación. Pendiente es el grado de inclinación de una superficie. La pendiente de una ubicación en particular se calcula como la tasa máxima de cambio de elevación entre esa ubicación y sus alrededores. La pendiente se puede expresar en grados o en porcentaje. La orientación de la dirección de la pendiente máxima medida en el sentido de las agujas del reloj en el intervalo [0, 360], donde 0º representa orientación al norte, 90º orientación al este, 180º orientación al sur, etc. La pendiente es relevante para trabajos de ingeniería y riesgos naturales (por ejemplo, deslizamientos de laderas) (Van Westen, 2013). La orientación está relacionada con la insolación y, por tanto, tiene una gran relevancia para las plantas y el uso de la energía solar (Kumar et al., 1997).
En algunos casos puede ser necesario evaluar la similitud entre dos modelos digitales de pendiente u orientación, bien en el sentido de similitud, donde los dos modelos a comparar tienen la misma consideración, o en el sentido de control de calidad, donde uno de los modelos se considera como referencia o patrón (Ariza López, 2002). En cualquiera de los dos contextos, es más robusto trabajar con un conjunto de categorías, que se pueden modelizar mediante ley multinomial, que, con una variable continua como la pendiente, o circular como la orientación. Esto se ve reforzado si las pruebas estadísticas (test de hipótesis) se basan en diferencias relevantes y no en una perspectiva de igualdad exacta (véase Sección 2). Por ello, es relevante proponer controles de calidad para estos dos parámetros y, en este trabajo, se presenta una de las primeras propuestas de control basado en un test estadístico denominado “test de equivalencia”.
El objetivo de este trabajo es proponer un control de calidad de tipo temático (basado en clases), es decir, en clases o categorías de pendiente y orientación definidas a voluntad por parte del usuario, pero con una perspectiva de detectar diferencias relevantes entre el producto y la referencia, no de igualdad exacta, como es usual en los contrastes de hipótesis al uso, si no permitiendo una holgura en una medida de distancia entre el producto a evaluar y el producto-patrón o producto-referencia.
El documento se organiza de la siguiente manera, tras esta introducción, la sección 2 presenta el método estadístico que se propone, en el que se incluyen los resultados de un estudio de simulación para el estudio de la significación y potencia del test propuesto. La sección 3 ofrece un ejemplo de aplicación al caso de unos datos reales relativos a la zona de las Bárdenas Reales (Navarra, España). Se analizará lo que ocurre con dos clasificaciones de las pendientes y con las orientaciones. La sección 4 presenta una discusión centrada en el método, sus aspectos más significativos y en los resultados de la aplicación desarrollada. Finalmente, la sección 5 se refiere a las conclusiones.
2. Metodología
Consideraremos que dada una variable genérica Y (pendiente u orientación) se va a categorizar atendiendo a un conjunto de tolerancias o umbrales que determinarán la definición de cada categoría. Supondremos que el número de categorías es k por lo que dada una muestra aleatoria simple de n observaciones de la variable Y, el vector que recoge conjuntamente el número de observaciones en cada categoría, X= (X_1, X_2, …, Xk)’;, sigue una distribución multinomial de parámetros n y P= (p1, …, pk)’;, pi > 0,1 ≤ i ≤ k,∑ ki=1p1 = 1, donde pi representa la probabilidad de ocurrencia asociada a la categoría i-ésima, X→M(n, P).
Por otro lado y dado el conjunto de referencia, la clasificación anterior aplicada sobre él nos proporciona el vector P0 = (p01, …, p0k)’; que representa los valores de referencia que determinarán los criterios de calidad para la clasificación de la variable Y. Nótese que los porcentajes indicados en P0 son fijos y se obtienen como la probabilidad de que la variable Y tome valores en el intervalo que define cada categoría sobre el MDE de referencia.
Nótese que el vector P0 puede incluso venir definido por el usuario (experto) a partir de las proporciones observadas sobre la categorización utilizada en otros modelos digitales (anteriores en el tiempo o en otras áreas de estudio).
Para determinar si los niveles de calidad indicados por la categorización en un conjunto de datos de referencia se alcanzan por parte del producto, existen una variedad de test de hipótesis que permiten dar una respuesta. Sin embargo todos ellos tienen en común la definición de una hipótesis nula formulada en términos de igualdad, P = P0 y una hipótesis alternativa en términos de desigualdad, P ≠ P0. En este tipo de test en el caso de que no existan evidencias para rechazar la hipótesis, la conclusión no debe ser que la hipótesis nula sea cierta. En otras palabras, puesto que el diseño de los test clásicos no está enfocado a la validación de la hipótesis nula, que no tengamos evidencia suficiente para rechazar que los niveles de calidad no se cumplen (P ≠ P0), no significa que dichos niveles se hayan alcanzado (P = P0).
El objetivo de este trabajo es proponer un procedimiento formal (test estadístico) para determinar si los niveles de calidad de un producto MDE se alcanzan en el sentido de que las diferencias entre P y P0 son suficientemente pequeñas como para considerar que ambas distribuciones multinomiales son iguales excepto “desviaciones irrelevantes”.
Para cuantificar el grado de similitud entre P y P0 vamos a considerar como medida de distancia el cuadrado de la distancia de Hellinger. Esta opción no es casual, esta medida de distancia se ha utilizado previamente con buenos resultados en problemas inferenciales relacionados con la distribución multinomial. Destacamos su uso en el estudio de similaridad de patrones espaciales de puntos (Alba-Fernández y Ariza-López, 2018; Alba-Fernández et al., 2016) o de la similaridad temática mediante matrices de confusión (García-Balboa et al., 2018).
Consideremos H(P, P0) como el cuadrado de la distancia de Hellinger entre P y P0 definida como
(1)
Para un valor ε>0, se plantea el siguiente contraste de hipótesis, conocido también como test de equivalencia
(2)
Puesto que 0 ≤ H (P, P0) ≤ 2 y H (P, P0)= 0 si y solo si P = P0, rechazar H0 supone que las distribuciones multinomiales son iguales excepto desviaciones irrelevantes dado el valor residual de ε.
Destacamos que el planteamiento de las hipótesis nula y alternativa en un test de equivalencia contrastan con la formulación de un test “clásico” de una hipótesis nula de “igualdad” frente a una alternativa de “no igualdad”. Ahora, en el test de equivalencia planteado, rechazar H0e supondrá que las distribuciones con vector de probabilidades P y P0 son prácticamente iguales atendiendo a la distancia considerada entre ellas. Por lo tanto, la conclusión del rechazo es confirmatorio sobre la verdadera distribución que representa los datos observados, es decir, es una prueba de validación de que los niveles de calidad marcados por el conjunto de referencia a través del modelo multinomial, M (n, P0), se alcanzan por parte del producto, M (n, P).
En este contexto, dado el vector de frecuencias relativas 
, que es el estimador de máxima verosimilitud de P, y a partir de H(P̂, P0), estimador consistente de H(P, P0), el resultado del Corolario 3.1 en Zografos et al. (1990) para P ε H0e, nos permite obtener la distribución asintótica de H(P̂, P0),
(3)
cuando n → ∞, donde:
(4)
y 
identifica convergencia en distribución.
Tomando 
como estimador consistente de 
, se verifica que
, (5)
cuando n → ∞.
Por tanto, dado un nivel de significación α є (0,1), rechazaremos la hipótesis nula H0e si
(6)
siendo Zα el percentil α de la distribución normal estándar.
A partir de este resultado, el test que rechaza H0e según (6) tiene asintóticamente nivel de significación α y es consistente frente a cualquier alternativa fija.
2.1. Estudio del nivel de significación
El test de equivalencia presentado se basa en el comportamiento asintótico del test estadístico Tn. Es decir, para un valor de ε, y para un nivel de significación α, la distribución asintótica, para tamaños de muestra grandes, es una distribución normal estándar.
Sin embargo, para tamaños de muestra pequeños o moderados se hace necesario analizar el comportamiento del test. En concreto, se ha diseñado un conjunto de simulaciones para evaluar sobre datos simulados el nivel de significación y la potencia del test teniendo en cuenta la relación existente entre el número de categorías k, el valor de є y el tamaño de muestra para que la aproximación de Tn a la distribución normal sea adecuada, todo ello, dado un nivel un significación fijado α є (0,1).
Con este objetivo, describimos brevemente las condiciones del estudio de simulación:
Se ha considerado 
para valores de k oscilando entre 3 y 7. La elección de este caso de estudio no es azarosa puesto que se ha utilizado ya previamente para estudiar el comportamiento de diversos test estadísticos vinculados a problemas de inferencia relacionados con la distribución multinomial (Alba-Fernández y Jiménez-Gamero, 2009; Basu et al., 2002; Pardo, 1999). Con respecto al número de categorías, creemos que se cubre el rango más habitual observado en las clasificaciones sobre la pendiente y orientaciones en un MDE (Elewa y Qaddah, 2011; Mikulski et al., 2014; Mogaji et al., 2015; Sheng, 1990; CEN prEN 1998-1, 2003; NTC, 2008).
Para el estudio del nivel de significación, debemos considerar casos incluidos en H0e. En particular, se han considerado un conjunto de configuraciones para P de forma que den lugar a unos valores de ε entre 0.1 y 0.2, alterando los porcentajes equiprobables de P0 en alguna o varias categorías. Los casos concretos utilizados en la simulación se presentan en la Tablas 1, Tabla 2 y Tabla 3, para los tres valores de k considerados.
Tabla 1 Configuraciones de P para k=3
| Casos | p1 | p2 | p3 |
| Caso 1 | 0.1758 | 0.1758 | 0.6483 |
| Caso 2 | 0.1433 | 0.1433 | 0.7133 |
| Caso 3 | 0.1167 | 0.1167 | 0.7667 |
Tabla 2 Configuraciones de P para k=5
| Casos | p1 | p2 | p3 | p4 | p5 |
|---|---|---|---|---|---|
| Caso 1 | 0.1350 | 0.1350 | 0.1350 | 0.1350 | 0.4600 |
| Caso 2 | 0.1400 | 0.1500 | 0.1400 | 0.1500 | 0.4200 |
| Caso 3 | 0.1535 | 0.1535 | 0.1535 | 0.1535 | 0.3860 |
Tabla 3 Configuraciones de P para k=7
| Casos | p1 | p2 | p3 | p4 | p5 | p6 | p7 |
| Caso 1 | 0.1300 | 0.1300 | 0.1300 | 0.1300 | 0.1300 | 0.1300 | 0.2200 |
| Caso 2 | 0.1229 | 0.1229 | 0.1229 | 0.1229 | 0.1229 | 0.1229 | 0.2629 |
| Caso 3 | 0.1155 | 0.1155 | 0.1155 | 0.1155 | 0.1155 | 0.1155 | 0.3071 |
Para cada configuración, P, se han generado muestras de la correspondiente multinomial, M (n, P), para varios tamaños de muestra n=50, 100, 200, 500 y se ha aplicado el criterio de decisión descrito en (6) para un nivel de significación α=0.05.
Repetido el procedimiento 100000 veces se ha determinado el porcentaje de rechazo de la hipótesis nula, lo que nos proporciona una estimación del error tipo I o nivel de significación α. La Tabla 4 y la Tabla 5, resumen los resultados obtenidos para cada valor de k.
Tabla 4 Porcentajes de rechazo para el nivel de significación del 5% (k=3 y k=5)
| k=3 | k=5 | |||||
| n | Caso 1 | Caso 2 | Caso 3 | Caso 1 | Caso 2 | Caso 3 |
| ε | 0.1 | 0.15 | 0.2 | 0.1 | 0.15 | 0.2 |
| 50 | 0.057 | 0.047 | 0.052 | 0.035 | 0.034 | 0.038 |
| 100 | 0.056 | 0.056 | 0.049 | 0.039 | 0.039 | 0.046 |
| 200 | 0.057 | 0.053 | 0.049 | 0.042 | 0.043 | 0.050 |
| 500 | 0.054 | 0.052 | 0.050 | 0.046 | 0.045 | 0.052 |
Tabla 5 Porcentajes de rechazo para el nivel de significación del 5% para k=7
| n | Caso 1 | Caso 2 | Caso 3 |
|---|---|---|---|
| ε | 0.1 | 0.15 | 0.2 |
| 50 | 0.019 | 0.022 | 0.023 |
| 100 | 0.027 | 0.028 | 0.029 |
| 200 | 0.033 | 0.034 | 0.033 |
| 500 | 0.038 | 0.040 | 0.040 |
| 1000 | 0.044 | 0.041 | 0.043 |
| 2000 | 0.046 | 0.044 | 0.044 |
Para el estudio de la potencia del test, debemos generar ahora bajo la hipótesis alternativa, por tanto, repetiremos los pasos 3) y 4) tomando como configuración para P el caso P0 para n=50, 100, 200. La Tabla 6 muestra los valores estimados de la potencia tomando ε=0.15 y α=0.05.
Tabla 6 Estimaciones de la potencia para un nivel de significación del 5%
| n | k=3 | k=5 | k=7 |
|---|---|---|---|
| 50 | 0.999 | 0.995 | 0.977 |
| 100 | 1 | 1 | 1 |
| 200 | 1 | 1 | 1 |
Puesto de dichos porcentajes de rechazo presentados en la Tabla 4 y la Tabla 5 representan las probabilidades estimadas de tipo I (nivel de significación), podemos observar cómo para valores pequeños de k, dicho nivel se alcanza para tamaños de muestra bajos (n=50 para k=3, independientemente del valor de ε), mientras que la aproximación a la distribución normal en (5) requiere tamaños de muestra superiores conforme el valor de k va aumentando o el valor de ε va disminuyendo. Para tamaños de muestra para los que las probabilidades estimadas de tipo I son inferiores a 0.05, el test es conservativo, es decir, rechaza en menor medida que el nivel de significación. Sin embargo, para este nivel de significación (5%), la potencia del test es muy elevada.
3. Aplicación
Para demostrar la aplicación del enfoque y métodos propuestos, se va a trabajar con datos correspondientes a dos productos MDE de los que se derivarán sendos modelos de pendientes y orientaciones. El área de trabajo se corresponde con una zona de las Bárdenas Reales (provincia de Navarra, España), que está delimitada por la hoja 0245 del Mapa Topográfico Nacional de España. Los productos originales son:
MDE02. Modelo digital de elevaciones de paso de malla de 2x2 m procedente de un levantamiento LiDAR del año 2017, dentro del proyecto PNOA (Plan Nacional de Ortofotografía Aérea, https://pnoa.ign.es/el-proyecto-pnoa-lidar).
MDE05. Modelo digital de elevaciones de paso de malla de 5x5 m procedente de un levantamiento LiDAR del año 2012, dentro del proyecto PNOA.
Ambos conjuntos de datos están disponibles en el centro de descargas del Centro Nacional de Información Geográfica (España) (http://centrodedescargas.cnig.es/CentroDescargas). La Figura 1 muestra el MDE sobre la zona de estudio.
Fuente: Elaboración propia a partir de datos del IGN.
Figura 1 Modelo de elevaciones (Bárdenas Reales, Navarra, España).
De los modelos anteriores, y por medio de operaciones convencionales de análisis SIG de la caja de herramientas de ArcGIS, se han derivado los modelos de pendientes (PTE02 y PTE05) y orientaciones (ORI02 y ORI05). En este trajo los modelos de menor paso de malla (2x2 m) son utilizados como referencia o patrón y los de mayor paso de malla (5x5 m) como producto a evaluar.
3.1 Pendiente
En esta zona de estudio, se han considerado dos clasificaciones para la pendiente. Cuando Dichas clasificaciones se aplican al modelo PTE02 dan lugar a los valores “patrón” que serán los consideraremos como valores fijos en el contraste (2) y que el producto PTE05 debe cumplir. En la Tabla 7 y la Tabla 8 se resumen dichos porcentajes, cuya representación espacial se muestran en la Figura 2.
Tabla 7 Clasificación #1.
| Grados | Clasificación | P0 |
| 0-1 | Llano | 0.23 |
| -1-7.5 | Moderado | 0.54 |
| >7.5 | Elevado y muy elevado | 0.23 |
Fuente: elaboración propia.
Tabla 8 Clasificación #2.
| Grados | Clasificación | P0 |
| 0-2 | Llano casi llano | 0.40 |
| 2-8 | Ligeramente inclinado | 0.38 |
| 8-15 | Fuertemente inclinado | 0.10 |
| 15-30 | Muy inclinado | 0.09 |
| >30 | Empinado | 0.03 |
Fuente: elaboración propia.
Recordemos que para un valor ε positivo y suficientemente pequeño, rechazar H0e supondrá que los valores “patrón” se han alcanzado. En nuestro caso, aplicamos (2) para ε=0.1, teniendo en cuenta que Zα=-1.645 para α=0.05. Para ello, hemos extraído muestras aleatorias simples de tamaños n=100, 200 y 500 para asegurarnos la correcta aplicación de la clasificación #2 independientemente del valor de ε. La Tabla 9 y la Tabla 10, muestran los porcentajes observados en el producto para cada clasificación, el estadístico de contraste Tn para cada caso y el resultado de la regla de decisión. Los resultados reflejados en ambas tablas nos llevan a la conclusión de que efectivamente los niveles de calidad representados por los valores “patrón” en el producto PTE05 se cumplen, tanto para la clasificación #1 como para la clasificación #2. Este nivel de cumplimiento debe entenderse como que la multinomial observada en PTE05 y la definida por el “patrón” (PTE02) son iguales, salvo diferencias mínimas en términos de la distancia de Hellinger.
Tabla 9 Aplicación del test de equivalencia sobre la clasificación #1.
| Tamaño de muestra | P̂ | Tn | Decisión |
| 100 | (0.280, 0.540, 0.180) | -12.73 | Rechazar H0e |
| 200 | (0.235, 0.550, 0.215) | -78.11 | Rechazar H0e |
| 500 | (0.240, 0.528, 0.232) | -167.23 | Rechazar H0e |
Fuente: elaboración propia.
Tabla 10 Aplicación del test de equivalencia sobre la clasificación #2.
| Tamaño de muestra | P̂ | Tn | Decisión |
| 100 | (0.38, 0.44, 0.09, 0.07, 0.02) | -13.46 | Rechazar H0e |
| 200 | (0.405, 0.400, 0.110, 0.070, 0.015) | -20.54 | Rechazar H0e |
| 500 | (0.382, 0.398, 0.112, 0.082, 0.026) | -67.12 | Rechazar H0e |
Fuente: elaboración propia.
3.2 Orientaciones
En el caso de las orientaciones, hemos considerado la clasificación usual en ocho sectores (N, NW, W, SW, S, …). Los valores de las proporciones correspondientes a estas categorías de orientación en ORI02 (datos de referencia), se muestran en la Tabla 11, en ella no aparece la categoría de terreno llano (sin orientación), pues es muy minoritaria y casi nula. Dichos valores vuelven a considerarse como el “patrón” que el producto ORI05 debe cumplir. La Figura 3 representa el modelo de orientaciones de esta zona.
Tabla 11 Clasificación de la orientación.
| Grados | Clasificación | P0 |
| 337.5-360, 0-22.5 | Norte (N) | 0.10 |
| 22.5-67.5 | Nordeste (NE) | 0.11 |
| 67.5-112.5 | Este (E) | 0.12 |
| 112.5-157.5 | Sureste (SE) | 0.12 |
| 157.5-202.5 | Sur (S) | 0.14 |
| 202.5-247.5 | Suroeste (SW) | 0.16 |
| 247.5-292.5 | Oeste (W) | 0.14 |
| 292.5-337.5 | Noroeste (NW) | 0.11 |
Fuente: elaboración propia.
Aplicamos nuevamente el test (2) con ε=0.1, y para asegurarnos la correcta aplicación del mismo, se ha seleccionado una muestra aleatoria simple de tamaño 500. Para dicha muestra, las frecuencias relativas observadas en cada categoría fueron 0.092, 0.116, 0.098, 0.122, 0.124, 0.160, 0.150 y 0.120, respectivamente. Para estos valores, el valor del estadístico de contraste fue Tn=-15.40 y puesto que Z0.05=-1.645, el criterio de decisión (6) en este caso da lugar al rechazo de la hipótesis nula, es decir, el cuadrado de la distancia de Hellinger entre el vector de frecuencias relativas y los valores “patrón” es inferior a 0.1 por lo que se considera que el producto ORI05 ha alcanzado los niveles de referencia para la clasificación de la orientación y que se han establecido por medio de ORI02.
4. Discusión
La discusión se va a desarrollar en tres líneas, la primera sobre el método, la segunda sobre sus aspectos más significativos, y la tercera sobre los resultados.
Consideramos que la aplicación del método es directa. Desde un punto de vista estadístico supone la realización de un contraste de hipótesis donde la hipótesis nula y la alternativa están establecidas de manera diferente a las hipótesis nula y alternativa convencionales que proponen una igualdad y una no igualdad. Esta diferencia supone por un lado un cambio conceptual en cuanto a lo que supone rechazar o no una hipótesis nula, aunque desde el punto de vista de los test estadísticos, no supone ningún tipo de cambio con respecto a la interpretación del nivel de significación y potencia asociados a todo test de hipótesis, pero este cambio en la formulación de las hipótesis, si introduce matices distintos sobre lo que se contrasta y, por ende, sobre lo que se acepta y rechaza desde el punto de vista del control de la calidad. La Tabla 12 resume estos cambios.
Tabla 12 Interpretación de los errores tipo I y II.
| Errores | Test clásico | Test de equivalencia |
| α=P[Rechazar H0/H0 cierta] (riesgo del productor) | Probabilidad de rechazar un producto cuando es bueno | Probabilidad de aceptar un producto malo cuando efectivamente lo es |
| β=P[No rechazar H0/H0 es falsa] (riesgo del usuario) | Probabilidad de aceptar un producto cuando es malo | Probabilidad de aceptar un producto malo cuando el producto es bueno |
| Potencia=1-β | Probabilidad de rechazar un producto cuando es malo | Probabilidad de aceptar el producto cuando el producto es bueno |
Fuente: elaboración propia.
En relación a los aspectos más significativos consideramos que éstos son el número de categorías, el tamaño de muestra y la distancia de Hellinger, los cuáles se encuentran muy interrelacionados en el método y necesitan un ajuste conjunto. El método se basa en la comparación de distribuciones multinomiales, por lo cual le es connatural el trabajar con categorías. El método se puede aplicar a variables categorizadas, pero en este trabajo se ha aplicado a variables continuas que se han discretizado. Estas categorías las puede definir el usuario a voluntad, pero su número no es un aspecto neutro. Un mayor número de categorías lleva a mayores tamaños de muestra, lo cual es lógico desde la perspectiva de los procesos de estimación sobre multinomiales.
Recordemos que la regla de decisión (6) se basa en la aproximación asintótica bajo H0 del estadístico de contraste Tn, y por tanto, el nivel de significación α se alcanzará de manera adecuada a partir de un determinado tamaño de muestra. Dicha aproximación se alcanzará para tamaños de muestra menores para valores de k menores (independientemente del valor de ε), y se hace más costosa en muestreo si k aumenta. Esta consideración es usual a otros test de hipótesis vinculados a la distribución normal, como por el ejemplo el test χ2 de Pearson, cuya aplicación se basa en aproximaciones asintóticas.
Por ello se recomienda tomar siempre el menor número de categorías posibles. En cualquier caso, consideramos que, con los ejemplos de aplicación mostrados, donde k=3, 5 y 8, se demuestra que se puede aplicar a los números de categorías más usuales.
Por otro lado, el test de hipótesis no se realiza sobre una medida natural al problema (p.ej. grados, radianes, metros, etc.), si no por medio de la distancia de Hellinger, la cual es desconocida para la que la mayoría de los usuarios y, aunque se entienda su base matemática, no se tiene demasiada sensibilidad sobre ella. Es decir, ¿ε = 0.1 es mucho o es poco? Para dar respuesta a esta pregunta debemos tener en cuenta la definición de H (P,P0), relacionada en cierta forma con la distancia euclídea sobre las raíces cuadradas de las frecuencias observadas y patrón, junto con el interés que el usuario ponga en que las “discrepancias” mencionadas sean o no de una determinada magnitud. En cualquier caso, esta limitación es muy usual en la aplicación de herramientas estadísticas a datos geoespaciales (p.ej. análisis cluster, etc.), donde aparecen diversas distancias (p.ej. Minkowski, Chebyshev, Manhattan, Mahalanobis, etc.) que tampoco son distancias “naturales” al problema. Esto conlleva la necesidad de alcanzar la suficiente sensibilidad en el manejo de la distancia que se aplica.
En el apartado 2.1 se ha desarrollado un estudio del nivel de significación que puede dar orientaciones para los casos que se han considerado en él, pero que también puede servir de guía para que los interesados en el método realicen sus ajustes entre número de categorías y ε.
No hay que perder de vista que el resultado es general para cualquier “patrón” P0 y que se puede adaptar a otro contexto distinto del planteado en el manuscrito (equiprobabilidad), para ello, basta repetir los pasos 1)-5) indicados en la sección 2.1 para el valor P0 objeto de estudio y otras configuraciones de P de forma que H (P0,P) = ε, para un ε>0 dado.
Finalmente, en relación a los resultados de los tres casos prácticos presentados, consideramos que se ha evidenciado la posibilidad de aplicación de esta metodología a las variables pendiente y orientación derivadas de MDE. Dado que los modelos MDE02 y MDE05 son de calidad alta, de fechas cercanas y que no han existido grandes cambios territoriales, el resultado de la aplicación es que los modelos derivados para las pendientes (PTE02 y PTE05), y para las orientaciones (ORI02 y ORI05), no muestran entre ellos diferencias superiores al valor de ε considerado. Un aspecto importante de la aplicación práctica es el tamaño de muestra necesaria para este control de calidad, el cual tiene repercusiones directas sobre el coste. En los ejemplos para la pendiente se han considerado tres tamaños de muestra (n=100, 200, 500) y, como se puede observar, en todos ellos se llega a la misma conclusión (rechazo de H0e). A mayor tamaño de n, el estadístico Tn obtenido también es mayor, lo que significa que se tiene más confianza en esta decisión. Por otro lado, también se evidencia que el crecimiento de Tn es menor con n en el caso de k=5 que en el caso de k=3, lo cual es lógico, pues mayor número de categorías requiere más esfuerzo muestral. En cualquier caso, el menor valor de Tn supera con creces el valor de Zα considerado, lo que permite considerar que se podrían utilizar tamaños de muestra algo menores, especialmente para k=3 donde es suficiente un tamaño de muestra de n=50 para obtener resultados fundamentados. Finalmente, en relación a la ejecución de estos muestreos en campo, no conviene olvidar que la medición de la pendiente y orientación en campo suele realizarse de manera simultánea o subrogada a otro tipo de trabajos (p.ej. catas edáfológicas), por lo que su disponibilidad estará en la mayoría de las veces condicionadas por este tipo de actuaciones.
5. Conclusión
En este trabajo se ha presentado una metodología para controlar algunas magnitudes derivadas de un MDE por medio de un proceso de categorización y del modelo multinomial resultante. Para realizar dicho control se propone un test de equivalencia cuya peculiaridad es el planteamiento de las hipótesis nula y alternativa a contrastar. En concreto se definen en términos de una medida de distancia entre la multinomial determinada por el producto y la correspondiente al conjunto de referencia, de forma que se considera que ambas distribuciones son equivalentes si el cuadrado de la distancia de Hellinger entre ellas es inferior a un umbral positivo y suficientemente pequeño ε.
Por otro lado, dado que los resultados del test se basan en la aproximación asintótica del estadístico de contraste a la distribución normal, hay que tener en cuenta el número de categorías y ε para determinar el tamaño de muestra necesario para su correcta aplicación, consideración por otra parte usual en test de hipótesis cuya regla de decisión se base en aproximaciones asintóticas.
El método se plantea de manera general para cualquier magnitud susceptible de ser categorizada, de tal manera que el punto de partida sea una distribución multinomial. Esto es, su uso es general y aplicable en otros contextos, como por ejemplo en control de la calidad temática en mapas de cobertura del terreno (en el contexto de las referencias García-Balboa et al., 2018), o en el estudio de la similaridad de patrones espaciales de puntos (en el contexto de las referencias Alba-Fernández et al., 2016 y Alba-Fernández y Ariza-López, 2018), entre otros posibles usos.
Se ha evidenciado la posibilidad de aplicación de esta metodología a las variables pendiente y orientación derivadas de MDE, no mostrando grandes diferencias entre los modelos derivados para las pendientes (PTE02 y PTE05) y para las orientaciones (ORI02 y ORI05).
