1. Introdução
O entendimento do tema de Medida é considerado central, em muitos contextos, como forma de desenvolver o Pensamento Matemático (National Council of Teachers of Mathematics [NCTM], 2000; Organisation for Economic Co-operation and Development [OCDE], 2010) dos alunos, e as noções de medida favorecem a conexão entre a Geometria e os Números, áreas particularmente críticas em termos de ensino e de aprendizagem (Clements & Sarama, 2007). Entender a Medida demanda atribuir significado aos seus elementos fundamentais - unidade de medida e todo a ser medido - e aos processos mentais envolvidos; e compreender as noções de quantidade, notadamente no que se refere à coordenação entre as quantidades discretas e contínuas (e.g., Smith et al., 2011). Tais entendimentos contribuem para desenvolver conhecimento associado aos fundamentos matemáticos de processos aritméticos; raciocínio proporcional; construtos e conceitos associados aos números racionais e à noção de variáveis algébricas (e.g., Szilagyi et al., 2013).
Há já consenso de que para ensinar Matemática é essencial ao professor conhecer ampla e profundamente os tópicos a serem ensinados (Ma, 1999). No entanto, o foco das pesquisas sobre o ensino de matemática tem sido maioritário nos conhecimentos dos alunos (Barret et al., 2012; Hiebert, 1984; Vysotskaya et al., 2020), deixando para segundo plano o conhecimento do professor e suas especificidades para ensinar, em particular, Medidas (Policastro et al., 2020; Ribeiro et al., 2018; Subramaniam, 2014). Sendo o conhecimento do professor um dos elementos que impacta nas aprendizagens e capacidades matemáticas dos alunos (Boyd et al., 2009; Hill & Chin, 2018) e nas ações e decisões que ele emprega em sua prática letiva (Charalambous, 2015; Ribeiro et al., 2012), torna-se essencial explorar algumas das especificidades desse conhecimento como forma de ampliar os entendimentos sobre seu conteúdo e as propostas de programas de formação de professores (Caldatto et al., 2018).
Diversas conceitualizações do conhecimento do professor surgiram nas últimas três décadas, porém destacam-se as que consideram a natureza especializada desse conhecimento (Scheiner et al., 2017) para a atuação docente. Uma delas é o Mathematics Teacher’s Specialised Knowledge - MTSK1 (Carrillo et al., 2018). Ao considerarmos a centralidade do entendimento da Medida nas aprendizagens matemáticas dos alunos (Clements & Stephan, 2004), o papel e a importância do conhecimento do professor nessas aprendizagens ((De Gamboa et al., 2020) e o ainda inexpressivo número de pesquisas específicas sobre as especificidades do conhecimento do professor para ensinar os tópicos de Medida (Di Bernardo et al., 2018; Ribeiro & Policastro, 2021), levam-nos a uma agenda de pesquisa que objetiva entender e descrever o conteúdo do conhecimento especializado do professor nos tópicos de Medida, com intuito de propor programas de formação que desenvolvam essas especificidades e, assim, melhorem a qualidade das discussões e das aprendizagens matemáticas. Nessa linha importa discutir a seguinte questão: Que conhecimento especializado dos tópicos de Medida revelam professores participantes de uma Formação Continuada focada nas especificidades do conhecimento do professor que ensina Matemática?
2. Fundamentos teóricos dos tópicos de Medida
Os tópicos de Medida e o “senso de medida” (Stephan & Clements, 2003, p. 14) deveriam ocupar um lugar de destaque nos currículos escolares, desde a Educação Infantil2, por se constituírem de elementos, noções e conceitos fundamentais ao desenvolvimento de ideias fulcrais da Matemática e ao envolvimento dos alunos com algumas das big ideas3 em Matemática (NCTM, 2000). No entanto, tradicionalmente, esse trabalho envolvendo Medida tende a focar-se no ensino das unidades de medida padronizadas (Policastro et al., 2017), sem explorar os procedimentos de medição para cada tipo de grandeza ou os processos (mentais) em que se pauta a atividade de medir (Stephan & Clements, 2003).
Do ponto de vista puramente experimental, medir está associado a conferir a um atributo mensurável de objetos, fenômenos ou processos (Berka, 1983) um valor numérico, obtido ao comparar magnitudes de uma mesma grandeza e quantificar as vezes que uma delas - a unidade de medida - deve ser repetida até que se consiga, por acumulação, obter a magnitude da outra - o todo a ser medido (Berka, 1983; Clements & Stephan, 2004).
No contexto dos tópicos de Medida, destacam-se as noções de “grandeza” e “magnitude” que, em muitos casos, por questões linguísticas4, são tomadas como sinônimos, mas aqui serão devidamente diferenciadas. Assume-se que grandeza é o atributo de um objeto ou fenômeno físico que pode ser quantificado por meio de um processo de medição, enquanto a magnitude é assumida como sendo a variação quantitativa deste atributo (Berka, 1983).
Ainda nesse contexto, outro termo que merece clarificação é “quantidade”. Com efeito, uma quantidade é um montante que pode ser determinado numericamente a partir de uma contagem ou a partir de uma medição. No primeiro caso, denominamos por “quantidade discreta” o valor determinado e, no segundo caso, falamos em “quantidade contínua” (Godino et al., 2002). As grandezas físicas (e.g., comprimento, área, volume, capacidade, tempo), possuem magnitudes expressas por quantidades contínuas. Mas a cardinalidade - número de elementos - de um conjunto, por exemplo, será sempre expressa por uma quantidade discreta. Dessa forma, tratamos as magnitudes como quantidades necessariamente associadas às medidas.
Habitualmente introduzem-se os alunos inicialmente às ideias de medição de comprimento, envolvendo instrumentos e unidades de medidas não padronizados (Smith et al., 2011). Posteriormente apresentam-se as unidades de medida padronizadas de comprimento, e todas as demais grandezas - área, capacidade, massa, volume e tempo5 - passam a ser discutidas, sem considerar as particularidades da natureza de cada uma (Ribeiro & Policastro, 2021; Sarama et al., 2011; Szilagyi et al., 2013). Segundo Lehrer et al. (2003, p. 100), as crianças deveriam ser engajadas a “desenvolver uma teoria sobre as medidas, ao invés de simplesmente efetuar medições”, e a conceitualização de cada uma das grandezas, através da comparação e classificação, deveria introduzir esse trabalho (Passalaigue & Munier, 2015).
Os processos (gerais) associados à atividade de medir estão fundamentados em seis princípios, descritos particularmente para o caso da grandeza comprimento (Clements & Stephan, 2004): (a) partição - atividade mental de dividir o objeto em magnitudes de mesmo comprimento, quando a unidade de medida é menor que o elemento a ser medido; (b) unidade de iteração - habilidade de pensar em um comprimento como referência para deslocar-se em todo o comprimento do objeto a ser medido, para não deixar espaços por medir entre duas unidades subsequentes, nem sobrepor unidades adjacentes; (c) transitividade - processo de, por estimativa ou dedução, obter uma relação de igualdade ou desigualdade (superior ou inferior) de quantidade relacionada a determinada grandeza e estendê-la a outros dois ou mais objetos; (d) conservação - compreensão de que qualquer movimento (translação ou rotação) no objeto a ser medido manterá os comprimentos; (e) acumulação da distância - entendimento de que, no processo de iteração de uma unidade de comprimento ao longo do elemento que se mede, realiza-se a contagem da quantidade de iterações; (f) relação da medida com um valor numérico - reorganização da compreensão do processo de contagem de quantidades discretas para quantidades contínuas.
Embora esses seis princípios tenham sido descritos com base nos processos (mentais e físicos) associados à atividade de medir unidimensionalmente, eles podem ser transpostos para grandezas de outros tipos, considerando algumas adaptações necessárias (Van den Heuvel-Panhuizen & Elia, 2011).
A noção de unidade de medida, porém, ocupa lugar de destaque nas aprendizagens matemáticas dos alunos, pois fundamenta vários outros conceitos como os de fração unitária e de todo e de unidade composta - unidade de unidades (Norton & Boyce, 2015). Mas essa unidade de medida é frequentemente confundida com o instrumento de medida (Gamboa et al., 2020). Nesse contexto, a noção de unitizing - operação mental na qual um agrupamento de quantidades pode ser interpretado como uma unidade (Steffe, 2003) - é fundamental para entender o que é e como se constitui uma unidade de medida.
Há várias questões ainda problemáticas para alunos e professores, sendo duas delas a diferenciação entre: (i) área e perímetro; (ii) volume e capacidade. Em (i), a dificuldade apresenta-se, essencialmente, pela não compreensão de qual o atributo (grandeza) a ser medido (Baturo & Nason, 1996). Com efeito, define-se área como a magnitude de uma superfície bidimensional contida por uma fronteira, e o perímetro, como a magnitude dessa fronteira (Clements & Sarama, 2009), o que demanda compreender que o perímetro é uma medida unidimensional (Irwin et al., 2004) e a área está subordinada à coordenação entre duas dimensões (Panorkou, 2020). Em (ii), as dificuldades sustentam-se porque os termos “volume” e “capacidade” são tomados como sinônimos (Ribeiro & Policastro, 2021), o que leva muitas vezes a associarem, nos contextos de ensino, as mesmas unidades de medida (padronizadas) às duas grandezas (Ho & McMaster, 2019), sem realizar o necessário trabalho que priorize a conceitualização de cada uma (Passalaigue & Munier, 2015). Essas dificuldades sustentam-se, também, pelo foco nos procedimentos de cálculo, sem conceitualizar a grandeza, ao assumir que calcular o valor da medida de uma grandeza seja medi-la.
3. Conhecimento do professor dos tópicos de Medida, na perspectiva do MTSK
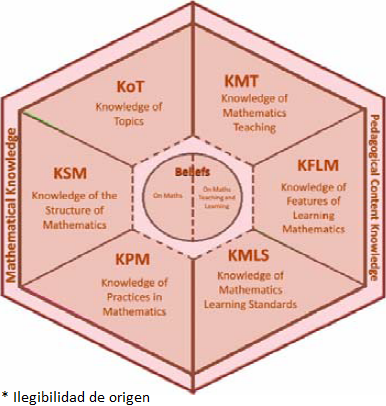
O Mathematics Teacher’s Specialised Knowledge - MTSK - (Carrillo et al., 2018) assume a natureza especializada do conhecimento do professor, considerando três domínios: Mathematical Knowledge (MK); Pedagogical Content Knowledge (PCK) e Beliefs a respeito da matemática e do seu ensino e aprendizagem. No MK consideram-se três subdomínios (ver Figura 1), mas aqui focamos somente o Knowledge of Topics (KoT).
Este estudo foca-se especificamente no KoT, uma vez que é a partir deste subdomínio que se pode evidenciar o conteúdo do conhecimento do professor acerca dos elementos estruturais e estruturantes de cada um dos tópicos matemáticos com os quais irá lidar em sua prática letiva.
Com efeito, o KoT corresponde ao conteúdo do conhecimento conceitual e procedimental do professor, relacionado a cada tópico. Originalmente consideram-se no KoT quatro categorias: (i) Definitions, properties and foundations; (ii) Phenomenology and applications; (iii) Procedures; (iv) Registers of representation (Carrillo et al., 2018). Porém, resultados recentes (Policastro & Ribeiro, 2021) mostraram a necessidade de separar a categoria (i) em (ia), (ib) e (ic), contribuindo para refinar o entendimento das especificidades do conteúdo do conhecimento do professor, relacionadas a cada um dos tópicos matemáticos.
Assim, a seguir, passamos a detalhar cada uma das categorias, no sentido de configurar particularidades e especificidades do conteúdo do conhecimento do professor associado a cada uma delas, especificamente no âmbito dos tópicos de Medida. Esse detalhamento teórico sustentará as análises e discussões realizadas na seção seguinte.
(ia) Definitions
As definições são essenciais na (Educação) Matemática, assumindo papéis e características muito específicos (Zaslavsky & Shir, 2005). Estes papéis relacionam-se com a apresentação dos objetos de uma teoria e a captura da essência dos conceitos, ao comunicarem suas propriedades caracterizadoras (Mariotti & Fischbein, 1997) e os elementos fundamentais para a formação desses conceitos (Vinner, 2002). Além disso, pelas definições é que se fundamentam as demonstrações e a resolução de problemas (Weber, 2002), porque se cria uma uniformidade na comunicação de ideias matemáticas importantes (Zazkis & Leikin, 2008).
As definições que o professor conhece influenciam nas aprendizagens dos alunos (Zazkis & Leikin, 2008), porque contribuem para estabelecer relações entre a imagem do conceito e a sua definição (Tall & Vinner, 1981). Inclui-se no conhecimento do professor conhecer que: o conceito de medida implica a comparação entre magnitudes de uma mesma grandeza, seguida da quantificação de uma delas - unidade de medida - em função da outra, o todo a ser medido (Berka, 1983); unidade de medida é definida como a magnitude de uma grandeza com a qual se pode medir outra magnitude desta mesma grandeza; que a área é uma grandeza que pode ser definica como a superfície delimitada pela fronteira de uma figura geométrica; o perímetro em duas dimensões é a linha que define a fronteira de uma figura plana; volume é a porção de espaço ocupada por um objeto no espaço; capacidade é o espaço interno de um objeto tridimensional, que pode ser preenchido (Panorkou, 2021).
(ib) Foundations
Um dos aspectos intrínsecos da prática matemática é a possibilidade de criar relações entre áreas aparentemente diferentes. Com efeito, “qualquer tipo de fundamento, se não define, pelo menos distingue entre trabalho matemático e não matemático e, de alguma forma, caracteriza a prática matemática, como sendo de um certo tipo e obedecendo a algumas regras específicas” (Venturi, 2014, p. 46). Se as propriedades matemáticas contribuem para organizar os conceitos, os fundamentos exercem o papel de os conectar. Os fundamentos são, portanto, responsáveis por criar elementos unificadores dos construtos e conceitos matemáticos, dando forma ao conhecimento matemático.
Inclui-se aqui o conhecimento do professor, associado a conhecer que: o que se mede são propriedades mensuráveis dos objetos ou fenômenos - as grandezas; unidade e instrumento de medida são elementos distintos; os constructos “comparar”, “iterar”, “acumular” e “quantificar” são fundamentos da atividade de medir qualquer grandeza (Berka, 1983; Clements & Stephan, 2004) com unidades padronizadas ou não padronizadas dessa grandeza; a iteração é um processo associado a um conjunto de comandos e ações que são repetidos de forma idêntica, até que se obtenha determinado resultado (Clements & Stephan, 2004); a unidade de medida e o todo a ser medido são expressos por magnitudes de uma mesma grandeza; as unidades de medida (padronizadas ou não) são adequadas para cada tipo de grandeza; a unidade de medida é um elemento fundamental no processo de medição (Bragg & Outhred, 2004; Norton & Boyce, 2015); e que é relevante o papel das unidades não padronizadas para fundamentar noções de grandezas e de suas respectivas unidades de medida padronizadas (Barrett et al., 2011; Bragg & Outhred, 2004).
(ic) Properties
As propriedades são “relações entre elementos ou subconjuntos de elementos de um conjunto que são instanciadas em situações particulares” (Mason et al., 2009, p. 10). A natureza dessas propriedades matemáticas pode variar; entretanto, o papel que elas exercem no entendimento dos conceitos e dos construtos matemáticos aos quais estão vinculadas é essencialmente o mesmo: organizar e descrever um conjunto de atributos e características relacionados especificamente a certos objetos ou entes matemáticos, de modo a que fiquem evidentes as relações entre eles. Inclui-se, no contexto da Medida, o conhecimento de que: toda unidade de medida, padronizada ou não, possui (sub)múltiplos resultantes do estabelecimento de relações de equivalência entre magnitudes da grandeza à qual a unidade está associada (Ribeiro & Policastro, 2021); a magnitude de qualquer grandeza, ou unidade desta, é expressa necessariamente por uma quantidade contínua (Bragg & Outhred, 2004); um instrumento não padronizado para medição de comprimento pode fornecer distintas unidades de medida (Policastro et al., 2017).
(ii) Phenomenology and applications
Nesta categoria inclui-se o conhecimento do professor não só dos conceitos que, dentro de um tópico, organizam e descrevem os fenômenos que dão sentido a esse tópico, mas também dos contextos que organizam todos os fenômenos que compartilham de ideias-chave ou “características estruturais” (Gómez & Cañadas, 2016, p. 316) próprias desses fenômenos. No âmbito dos tópicos de Medida, inclui-se conhecer que medir é comparar magnitudes de uma mesma grandeza em termos da quantificação de uma em função da outra e conhecer os distintos contextos de aplicação da atividade de medir: perímetro, área, capacidade, volume, massa, etc.
(iii) Procedures
Conhecer um conjunto de procedimentos associados a cada um dos tópicos- que muitas vezes se configuram como algoritmos -, os porquês matemáticos que os sustentam, a característica do resultado obtido e as condições necessárias e suficientes para executar tais procedimentos, forma parte desta categoria. No âmbito da Medida, inclui-se, por exemplo, conhecer: os procedimentos de iteração para efetuar uma medição de qualquer grandeza, isto é, a unidade de medida deve ser iterada até completar o todo a ser medido, sem que se deixem lacunas ou se sobreponham unidades ao longo da iteração; que um instrumento de medida não padronizado pode ser utilizado de forma padronizada (ou não) para efetuar uma medição (Ribeiro et al., 2018); que o resultado da uma medição caracteriza-se pelo valor da medida expressa por um número associado a uma marca, e esta marca corresponde à unidade de medida utilizada (padronizada ou não); que é condição necessária para efetuar uma medição que a unidade de medida seja única, ainda que essa unidade seja resultante de uma composição de unidades (Norton & Boyce, 2015).
(vi) Registers of representation
O conhecimento matemático é exteriorizado e percebido pelos sentidos, e essa exteriorização pode ocorrer associada a distintas formas de o tornar perceptível. Essas múltiplas formas correspondem a registros de representação (Ainsworth, 2006; Pape & Tchoshanov, 2001) que podem ser, por exemplo, numéricos, pictóricos, gráficos, verbais - em linguagem oral ou escrita. Como elementos desta componente no âmbito da Medida, inclui-se, por exemplo, conhecer diferentes formas de exteriorizar uma medida; relacionar distintos registros de representação e navegar frutiferamente entre eles; ou compreender o emprego do termo “tamanho” como inadequado para se referir à magnitude de qualquer grandeza.
4. Contexto e método
Esta investigação compõe uma agenda de pesquisa que busca caracterizar, em vários temas e tópicos matemáticos, o Conhecimento Especializado do professor que atua desde a Educação Infantil. Aqui discutimos alguns aspectos desse conhecimento no âmbito de distintos tópicos do tema de Medidas. É um estudo de caso instrumental (Stake, 1995), cujo foco de interesse não é o caso em si, mas saber que este instrumento permite conhecer e entender um elemento específico - o conhecimento do professor -, de modo a gerar teorias. As informações foram coletadas em um contexto de um Programa de Formação Contínua6 - com sete módulos de formação - que envolveu 17 professores, atuantes desde a Educação Infantil ao Ensino Superior, e que teve o objetivo formativo de desenvolver o conhecimento dos participantes, na perspectiva do MTSK, em vários tópicos matemáticos.
Cada um dos módulos do programa focava em um tema matemático considerado problemático - conforme pesquisas na área de Educação Matemática apontam -, tanto do ponto de vista das aprendizagens dos alunos quanto do processo de ensino, a saber: Números e Operações, Frações, Geometria (dois módulos), Pensamento Algébrico, Probabilidade e Estatística e Medidas.
No programa de formação, aos professores não era atribuído o papel de ativamente decidirem os tópicos que seriam abordados em cada encontro, embora também não lhes fosse vetado o direito de sugeririem ou solicitarem que determinados tópicos fossem incluídos nas discussões. Por exemplo, no caso do módulo de Medidas (o último do programa), embora o tópico de divisão de frações não estivesse inicialmente contemplado no programa, esse assunto foi incluído e abordado a pedido dos cursistas, em uma das cinco sessões de formação do módulo.
Neste estudo, focamos em uma das sessões de formação (carga horária de 8 horas) do módulo de Medidas7. No contexto formativo do programa mencionado, todos as sessões de formação eram gravadas em áudio e vídeo - tomando-se um plano geral das discussões em grande grupo e planos com foco em cada um grupo de trabalho - em geral, quatro grupos.
Nesse encontro, os professores foram convidados a refletir sobre a Tarefa para a Formação - TpF (Ribeiro, Almeida & Mellone, 2021), intitulada “A Medida, seus princípios, fundamentos e procedimentos”. Com efeito, a conceitualização de uma TpF se dá com base na lente teórica do MTSK, que é utilizada como ferramenta para incluir propostas nas tarefas que efetivamente contribuam para mobilizar elementos do conhecimento especializado dos professores, associados a cada um seis dos subdomínios (KoT, KPM, KSM, KFLM, KMT e KMLS), considerando não só as particularidades de cada tópico matemático em foco na formação, mas também, e obviamente, os objetivos formativos previamente delineados.
Assim, para discutirem as propostas da TpF, os 17 participantes da sessão, identificados por “Pi” em que i é um número que corresponde a um professor, foram organizados em quatro grupos: Grupo 1 - três professores atuantes nos Anos Iniciais (P3, P4 e P11) e um estudante de pedagogia (P13); Grupo 2 - quatro professores atuantes nos Anos Iniciais (P2, P8, P9 e P17) e um professor atuante no Ensino Médio e Superior (P10); Grupo 3 - um professor atuante na Educação Infantil (P1); dois professores atuantes nos Anos Finais (P5 e P7) e um estudante de pedagogia (P16); Grupo 4 - um professor atuante na Educação Infantil e Anos Iniciais (P6), um professor atuante nos Anos Iniciais (P13), um professor atuante nos Anos Finais (P14) e um professor que não atua mais no mercado de trabalho (P15). Note-se que cada grupo sempre esteve constituído por professores atuantes (ou em formação) de diferentes níveis de ensino, justamente para que fossem estimulados a compartilhar suas experiências e perspectivas relacionadas com as discussões mobilizadas pela TpF.
Partimos, então da TpF (Ribeiro et al., 2021) e focamos a atenção nas produções e discussões dos professores, associadas a três questões da Parte I da TpF (Figura 2) e a questões vinculadas a uma tarefa para os alunos (Figura 5).
A primeira questão foca-se nos construtos e conceitos que fundamentam o fenômeno e os procedimentos da atividade de medir; a segunda associa-se ao conhecimento do professor dos níveis conceituais e procedimentais dos alunos em etapas educativas distintas, com relação aos fundamentos da atividade de medir; a última questão busca ampliar a discussão em relação ao papel das unidades de medida na medição. O conteúdo da segunda questão pode ser tipicamente entendido como estando associado ao domínio do PCK (particularmente, ao subdomínio KMT), mas o foco aqui é no conhecimento matemático manifestado na justificação.
Todas as TpF (Ribeiro, 2021) contêm uma tarefa para alunos, e aqui essa tarefa contribuiu para aceder ao conhecimento dos participantes - e desenvolvê-lo - quanto aos princípios, fundamentos e procedimentos associados à atividade de medir.
Esta tarefa para os alunos incluiu uma abordagem de “metodologias ativas” e continha indicações para a passagem por diferentes estações de trabalho (Figura 3); uma ficha de registro de respostas (Figura 4); e um conjunto de perguntas associadas (Figura 5).
Os professores resolveram a Parte I (Figura 2) nos pequenos grupos, e uma discussão plenária foi realizada. Posteriormente resolveram a tarefa para alunos, percorrendo as estações e finalizaram com outra discussão plenária.
O áudio captado durante as interações - nos pequenos grupos e plenárias - foi integralmente transcrito e complementado com informações identificadas nos vídeos (Ribeiro et al., 2012). Na transcrição, as linhas são numeradas, e “Pi” corresponde a algum dos professores i (de 1 a 17) e a formadora, que é uma das autoras deste trabalho está identificada por F. A análise foi realizada em duas fases, uma manual e outra com o auxílio do software ATLAS.ti, procurando evidências de conhecimento no âmbito das categorias do KoT. Ao inserir os documentos no ATLAS.ti, as transcrições foram identificadas por “ME.I.N”, e os registros escritos digitalizados foram identificados por “T.I.N”, em que “N” representa o número do grupo em que ocorreram as discussões, e, para as plenárias, usou-se a nomenclatura “ME.PL.I”.
Após alguns ciclos de codificações, incluindo-se, excluindo-se ou reagrupando-se as produções dos professores e determinadas categorias do KoT, até atingir a saturação (Strauss & Corbin, 1994), identificaram-se 473 produções, evidenciando conteúdo conhecimento especializado (ver Tabela I), relacionado ao KoT.
Tabela I Incidência de produções associadas a evidências do conhecimento em cada categoria do KoT
| Categorias do KoT | Produções |
| Definitions | 51 |
| Foundations | 218 |
| Properties | 42 |
| Phenomenology and applications | 14 |
| Procedures | 121 |
| Registers representation | 27 |
| Total | 473 |
Uma análise transversal e longitudinal buscou semelhanças e diferenças entre o conteúdo do conhecimento identificado. Refinando a cada ciclo de análise, emergem os denominados descritores de conhecimento do professor (Policastro & Ribeiro, 2021), nomeados de acordo com o subdomínio (KoT) e a categoria a que pertencem: (Definitions (d); Foundations (f); Properties (pp); Phenomenology and Applications (ph); Procedures (mp); Registers of representantion (rp)). A cada um foi atribuído um número sequencial.
Na Tabela II exemplificamos como esses descritores emergem da análise. Os professores revelam conhecimento associado a Definitions: ao buscarem explicar e conceituar o que é medir (ME.I.2, 46-48; ME.I.3 e T.I.1); e ao referirem certos entes - instrumento e unidade - que consideram necessários na atividade de medir (ME.I.3, 1033-1040).
Tabela II Reagrupamento das produções e emergência dos descritores de conhecimento
| Definitions | ||
| Produções dos professores | ||
|
ME.I.2 T.I.1 “Medir é especificar o tamanho de determinadas coisas.” |
ME.I.3
|
|
| Análise | ||
| Conhecimento de que a medida está associada à comparação de uma unidade de medida (denominada majoritariamente por “referência”) com um todo, seguida de quantificação e/ou atribuição de um valor numérico. | Não fazem distinção entre unidade de medida e instrumento de medição. Revelam entender que a unidade de medida se relaciona com uma magnitude, mas alguns professores confundem unidade de medida com grandeza. | |
| Descritores emergentes | ||
| KoTd1 - conhecer a definição de medida: relação numérica entre magnitudes de uma mesma grandeza, obtida por comparação seguida de quantificação de uma dessas magnitudes (todo a ser medido) em função da outra (unidade de medida). | KoTd5 - conhecer a definição de unidade de medida: uma magnitude de uma grandeza com a qual se pode medir outra magnitude dessa mesma grandeza. | |
Em alguns casos, o conteúdo do conhecimento revelado pelos professores foi identificado como matematicamente inapropriado, fosse por incorreções conceituais ou por inadequações de contextos em que esses conceitos eram evocados. Em outras situações suas produções não exteriorizaram, de forma explícita, elementos suficientes para caracterizar o conteúdo do conhecimento, mas a discussão conjunta com os fundamentos teóricos assumidos para a análise permitiu constituir tais descrições. Nesse sentido os descritores emergentes dessas produções são identificados, respectivamente, com os símbolos “*” e “**” associados, sendo KoTph2* e KoTf2** dois exemplos.
Das 473 evidências identificadas, sintetizamos 31 descritores: 6 relacionados com Definitions; 8 com Foundations; 5 com Properties; 2 com Phenomenology and applications; 8 com Procedures; e 2 com Registers of representation. A ordem da numeração dos descritores está relacionada exclusivamente com a quantidade de produções dos professores vinculadas a cada um deles, ou seja, quanto maior o número de produções associadas, menor é a numeração do descritor. Portanto, KoTd1 tem mais produções associadas do que KoTd5, por exemplo. Assim, não seguimos uma ordem sequencial na numeração dos indicadores de cada categoria, mas uma numeração por “pesos”.
5. Resultados e discussão
Todos os grupos de professores consideraram que medir é comparar uma unidade de medida (que denominam “referência”) com um todo, seguido de quantificação e atribuição de um valor numérico (KoTph1 - conhecer que medir é comparar magnitudes de uma mesma grandeza em termos da quantificação de uma em função da outra).
Ao assumirem a comparação como um construto fundamental para a medição (ME.I.4: 54), reconhecem sua relação com uma etapa inicial do processo completo de medir, mas incluem outros (Berka, 1983; Clements & Stephan, 2004), como é o caso da quantificação (ME.I.4: 55) (KoTmp6 - conhecer que a comparação é uma condição necessária, mas não suficiente para medir).
Apesar de não ficar claro se entendem os processos “quantificação” e “atribuição do valor numérico” como um único processo ou como processos distintos (ME.I.2: 84 - 90), reconhecem que há processos (mentais) e construtos fundamentais presentes em toda atividade de medição (Berka, 1983; Clements & Stephan, 2004) (KoTf2** - conhecer que os construtos “comparar”, “iterar”, “acumular” e “quantificar” são fundamentos da atividade de medir qualquer grandeza).
Revelam também um conhecimento associado aos fenômenos e aos contextos de aplicação (Gómez & Cañadas, 2016) dos fundamentos da atividade de medir (ME.I.3: 367 - 370), mesmo quando sugerem a presença desses fundamentos em contextos a que efetivamente não estão associados (KoTph2* - conhecer os distintos contextos de aplicação dos fundamentos da atividade de medir: medir comprimento, área, capacidade, massa, etc.).
Ainda relativo à “quantificação”, revelam conhecer que uma medida é dada por um valor expresso por uma quantidade contínua - embora não referindo explicitamente essa continuidade (ME.I.1: 304 - 310) -, em particular quando a medição é associada à grandeza comprimento. Essa interpretação pode ser dada em virtute da afirmação que P4 faz de que “quantificar está dentro de medida”, levando-nos a reconhecer que há um conhecimento mobilizado de que a quantificação pode se referir a quantidade contínuas ou discretas, mas que, no caso da contagem, a quantidade a que nos referimos é sempre do tipo discreta, o que não ocorre com a natureza da magnitude de uma medida (KoTpp3** - conhecer que a magnitude de qualquer grandeza, ou unidade desta, é expressa necessariamente por uma quantidade contínua).
Ainda que os professores reconheçam que o valor de uma medida pode ser expresso em termos de um número não inteiro (Smith et al., 2011) (KoTpp3**), particularmente quando lidam com medições em que a unidade de medida é não padronizada (e.g., arestas de um paralelepípedo), nem todos (ME.PL.I:1111 - 1114) consideram a possibilidade de que os valores numéricos das medidas possam ser expressos por múltiplos e submúltiplos dessa unidade de medida (KoTpp1 - conhecer que os múltiplos ou submúltiplos de uma unidade de medida - padronizada ou não - são estabelecidos por meio de relações de equivalências entre magnitudes da grandeza à qual a unidade está associada).
Consideram, inapropriadamente, que os submúltiplos de uma unidade correspondem a outra unidade distinta, algo que se relaciona com conhecer que toda unidade de medida possui múltiplos e submúltiplos (Berka, 1983) (KoTpp2*- conhecer que toda unidade de medida, padronizada ou não padronizada, possui múltiplos e submúltiplos).
Revelam também um conhecimento das relações entre múltiplos e submúltiplos, ao efetuarem uma transposição direta entre a estrutura do Sistema de Numeração Decimal (valor posicional) e as relações de equivalência entre múltiplos e submúltiplos de unidades padronizadas que possuem base 10 (M.E.I.3: 225-228), como é o caso de comprimento, capacidade e massa. No entanto, pautam-se em memorização de regras que nem sempre estabelecem congruências verdadeiras (KoTpp5* - conhecer as relações de equivalência estabelecidas entre múltiplos e submúltiplos de uma unidade de medida padronizada com estrutura decimal - base 10).
Quando as discussões se centram nas grandezas volume e capacidade (ME.I.2: 1468-1473), os professores revelam entender capacidade de um recipiente como a medida de “algo que cabe dentro” dele (Panorkou, 2021) (KoTd2 - conhecer que a definição de capacidade pode ser dada como o espaço interno de um objeto tridimensional que pode ser preenchido).
Corroborando a dificuldade para distinguir as grandezas volume e capacidade (Ho & McMaster, 2019), alguns professores consideram que somente os objetos sólidos (maciços) possuem volume, e objetos ocos possuem apenas capacidade (KoTd4 - conhecer que a definição de volume pode ser dada como a porção do espaço ocupado por um objeto tridimensional).
Entendem a grandeza área como o resultado do “preenchimento” de uma região (MEI.1: 657-659), definida uma unidade de medida, mas também como o resultado do produto de magnitudes unidimensionais, o que se associa com a coordenação entre duas dimensões (Panorkou, 2020), mas não entre duas unidades de medida (KoTd3 - conhecer que a área pode ser definida como a superfície delimitada pela fronteira).
Os professores não fazem distinção entre medir a área e calcular o valor da área de uma região (KoTmp3* - conhecer que efetuar uma medição não corresponde a calcular uma medida, mas sim estabelecer uma relação entre duas magnitudes de uma mesma grandeza) por meio de fórmulas matemáticas, especificamente no caso do retângulo (ME.I.3: 899-902) (KoTmp8 - conhecer o procedimento associado ao uso da fórmula para determinar o valor da grandeza área no caso do retângulo: efetuar o produto das magnitudes dadas em dimensões ortogonais).
Em contrapartida, particularmente no caso das figuras poligonais, os professores reconhecem que o perímetro não pode ser definido a partir do modo como é calculado (ME.I.3: 959-967) (KoTd6 - conhecer que a definição de perímetro - em 2D - é o comprimento da linha que define a fronteira de uma figura plana).
Outros dois construtos que os professores não distinguem (ME.I.1: 436-441) são unidade de medida e instrumento de medição (KoTf1* - conhecer a distinção entre unidade de medida e instrumento de medição).
Ao passarem pelas estações para resolver a tarefa para os alunos, onde deveriam medir a capacidade e a massa de alguns objetos utilizando diferentes instrumentos de medição (copo plástico e balança de cabide) e unidades de medida não padronizadas (capacidade do copo e massa de uma barra do material dourado), não diferenciaram instrumento de unidade de medida (KoTd5 - conhecer a definição de unidade de medida: uma magnitude de uma grandeza com a qual se pode medir outra magnitude desta mesma grandeza).
Mesmo assim, ao referirem o seu trabalho habitual com os alunos (Figura 19), particularmente no caso da grandeza comprimento, os professores revelam conhecimento do papel das unidades de medida não padronizadas no entendimento das grandezas padronizadas (Passalaigue & Munier, 2015) (KoTf4 - conhecer que as unidades de medida não padronizadas fundamentam as noções de grandezas e de suas respectivas unidades de medida padronizadas).
Identificam que um instrumento não padronizado (ME.I.1: 682-688) pode fornecer mais de uma unidade de medida (KoTpp4 - conhecer que um instrumento padronizado, ou não, para medição de comprimento pode ser empregue associado a distintas unidades de medida e a distintas grandezas) e revelam conhecer que instrumentos não padronizados (ME.I.1: 689-691) podem ser utilizados de forma não padronizada (Ribeiro et al., 2018) para medir distintas grandezas (KoTmp7 - conhecer que uma medição pode ser efetuada utilizando unidades não padronizadas de forma não padronizada: e. g., largura da caneta para medir comprimento; menor face de um prisma para medir a área de uma região).
No entanto, parece haver um “salto” entre o que os professores consideram como possibilidade de trabalho introdutório para a grandeza comprimento e o que se propõe para trabalhar com outras grandezas (Stephan & Clements, 2003). Em particular, para as grandezas capacidade e massa, revelam dificuldades (ME.I.4: 957-969) em conceber que uma medição pode ser efetuada com uma unidade de medida não padronizada, e resistem a aceitar o valor da medida correspondente obtido em termos dessa unidade (Bragg & Outhred, 2004) (KoTf4).
Essas dificuldades estão associadas a uma lacuna entre as discussões desenvolvidas no âmbito da grandeza comprimento e o que (não) se faz para a conceitualização das outras grandezas (Passalaigue & Munier, 2015), mas, fundamentalmente, vinculam-se ao conteúdo do conhecimento dos professores acerca de: o que é uma medida (KoTd1); o que é uma unidade de medida (KoTd5); os constructos que fundamentam a atividade de medir (KoTf2**); o entendimento de que o que se mede são as grandezas (KoTf3). De fato, assumem inapropriadamente (ME.I.1: 33 e 97-98) que grandeza é uma “característica” de um objeto físico (Berka, 1983), e não uma propriedade mensurável desse objeto ou de um fenômeno físico (KoTf3* - conhecer que o que se mede são grandezas que correspondem a propriedades mensuráveis dos objetos ou fenômenos).
O termo “tamanho” é utilizado de forma genérica pelos professores, principalmente associado ao comprimento - uso matematicamente inadequado -, o que revela seu conhecimento da nomenclatura da grandeza (KoTrp1* - conhecer a nomenclatura adequada para se referir a cada uma das grandezas). Ao mesmo tempo, revelam conhecimento da necessidade de uma nomenclatura matemática adequada (ME.I.1: 1659-1670), associada às unidades de medida (KoTrp2 - conhecer a nomenclatura e simbologia adequadas para se referir às unidades de medida: unidades padronizadas e não padronizadas).
Todos os professores reconhecem a importância do construto “unidade de medida” (Bragg & Outhred, 2004) e sabem que, sem ela, não se efetua uma medição (KoTf5 - conhecer que a unidade de medida é um elemento fundamental no processo de medição).
Somente dois dos quatro grupos (ME.I.2: 60-62) abordaram explicitamente um dos elementos do conhecimento dos fundamentos da Medida (KoTf6 - conhecer que a unidade de medida e o todo a ser medido devem ser de mesma natureza, ou seja, são expressos por magnitudes de uma mesma grandeza).
Esse fato associa-se a duas dimensões: por um lado, por não deterem um conhecimento associado à definição de medida (KoTd1), não consideram que a unidade de medida e o todo a ser medido tenham de ser magnitudes de mesma natureza. Por outro lado, a “comparação” entre uma unidade de “referência” e algo relacionado a essa referência é o construto que sustenta o conteúdo desse conhecimento; portanto, tal comparação só é possível entre magnitudes de mesma natureza, mas não distinguir unidade de instrumento de medição (KoTf1*) pode sustentar o não reconhecimento da necessidade de que as magnitudes da unidade e todo a ser medido sejam da mesma natureza.
Os professores revelam um conhecimento associado às unidades de medida padronizadas e não padronizadas mais comuns (KoTf7 - conhecer as unidades de medida padronizadas para cada grandeza).
Ao resolverem a tarefa dos alunos, revelam conhecer procedimentos de medição fazendo uso dos princípios essenciais da atividade de medir (Clements & Stephan, 2004). No entanto, solicitados a medir o comprimento de um elemento maleável - barbante - utilizando como instrumento de medida um elemento sólido - paralelepípedo -, os professores revelam dificuldades em aplicar esses princípios.
No procedimento descrito (ME.I.4: 680-686), P14 não considera que, ao dobrar o fio, uma porção do todo a ser medido - o comprimento do barbante - foi perdida, deixando lacunas entre as unidades de medida na iteração (Clements & Stephan, 2004). Apesar de a maioria efetuar o procedimento de iteração de forma adequada (descrito na Figura 28), não há menção explícita ao que sustenta tal procedimento (KoTmp1** - conhecer os procedimentos de iteração para se efetuar uma medição de qualquer grandeza: a unidade de medida deve ser iterada até completar o todo a ser medido, sem que se deixem lacunas ou se sobreponham unidades ao longo da iteração). Assim, pode ser algo que forma parte do script de medição, e não é, portanto, entendido como central nesse processo, que fundamenta a existência de um algoritmo a ele associado (KoTf8** - conhecer que a iteração é um processo associado a um conjunto de comandos que são repetidos de forma idêntica até que se obtenha determinado resultado).
Para medir uma distância (ME.I.3: 175-178), consideram a relação entre a magnitude da unidade de medida e a quantidade de vezes que terá de ser iterada para medir o todo (KoTmp4 - conhecer a característica do resultado de uma medição: o valor numérico (v) obtido na medição é inversamente proporcional à magnitude da unidade de medida (u), quando se considera constante a magnitude da mesma natureza do todo (d) a ser medido (v = d/u)).
Apesar de os professores associarem instrumento de medida com unidade de medida (ME.I.1: 412-413), destacam a necessidade (condição necessária) de que essa seja única no processo de medição. Porém, não fica claro se conhecem que na iteração sempre se deve utilizar a mesma unidade de medida (Norton & Boyce, 2015), ainda que ela seja formada pela composição de outras unidades (KoTmp5**: conhecer que é condição necessária para se efetuar uma medição que a unidade de medida seja única, ainda que essa unidade seja resultante de uma composição de unidades - unitizing).
No intuito de sintetizar os resultados obtidos neste estudo e de avançar na teorização desse conhecimento - por via dos descritores -, apresentamos uma caracterização obtida do conhecimento especializado do professor relativamente a tópicos de Medida - KoT.
Tabela IV Categorias e descritores relacionados ao subdomínio Knowledge of Topics de Medida
Fica evidente a prevalência de alguns descritores em detrimento de outros. Essas diferenças podem estar associadas, por um lado, ao fato de que a TpF (Ribeiro et al., 2021) não perseguia objetivos específicos associados à categoria Registers of representation. Por outro lado, os resultados da categoria Phenomenology and Applications são coerentes com estudos anteriores que identificaram seu conteúdo como o mais ausente (Gómez & Cañadas, 2016; Zakaryan & Ribeiro, 2018).
6. Comentários finais
Descrever, entender e caracterizar o conteúdo do conhecimento especializado de um grupo de professores de diferentes etapas educativas no âmbito da Medida contribui para clarificar certas particularidades e especificidades do conhecimento do professor que ensina ou ensinará os tópicos de Medida, independentemente da etapa educativa em que atua, uma vez que, particularmente no caso do subdomínio KoT (em foco neste trabalho), tal caracterização contribui para tornarem evidentes certos elementos estruturais e estruturantes do conteúdo do conhecimento do professor. Nesse sentido, são precisamente esses elementos estruturais e estruturantes que compõem o conteúdo do conhecimento docente em relação a cada tópico matemático que nos permitem considerar que, independentemente da etapa educativa em que este profissional atue, poderá mobilizar esses conhecimentos, quando inserido em uma prática letiva qualquer.
Notemos, além disso, que essa não associação entre essas especificidades e a etapa em que o professor atua contribui para que possamos encarar a matemática elementar de um ponto de vista avançado (Klein, 1932) e vice-versa, mas também para que possamos mapear esse conhecimento especializado, numa perspectiva de descompactá-lo (Ma, 1999) e torná-lo mais acessível a outros.
Naturalmente, a busca por esse mapeamento não pretende prescrever todo o conhecimento do professor, mas almeja fornecer elementos para que o professor se paute em “ideias centrais que determinam como o conhecimento é gerado e organizado dentro da disciplina” (Schmidt et al., 2002, p. 9).
Quando nos propomos a um detalhamento do conteúdo do conhecimento do professor, importa evidenciar as características e os elementos que constituem as especificidades desse conhecimento. Nesse sentido, pautados por resultados anteriores (Policastro & Ribeiro, 2021), passamos a considerar que o conteúdo do conhecimento do professor associado à categoria Definitions, properties and foundations (Carrillo et al., 2018), relativamente a qualquer tópico, mas aqui, em particular, nos tópicos de Medida, deveria ser encarado em termos de suas especificidades, de forma separada, em categorias distintas. De fato, os resultados obtidos permitem identificar, em específico nas categorias Properties e Foundations, componentes do conhecimento do professor que necessitam ser desenvolvidas.
Assim, é essencial que o desenho de programas de formação considere explicitamente estes e outros resultados, com objetivo de contribuir para desenvolver o conteúdo do conhecimento do professor que lhe permita, por exemplo, conectar conceitos, propriedades e fundamentos, e, na sua prática letiva - atual ou futura -, evidenciar essas conexões dentro de um mesmo tópico e entre tópicos distintos, dando forma à estrutura da disciplina (Gamboa et al., 2020). Para isso, é necessário um foco específico da formação, associado a tarefas desenhadas intencionalmente (Ribeiro, 2021; Ribeiro, Gibim & Alves, 2021) com a finalidade de desenvolver uma consciência das estruturas da matemática (Mason et al., 2009), do entendimento das conexões matemáticas e do conhecimento de como organizar, numa distribuição curricular, os tópicos, de modo a evidenciar essas conexões (Vale et al., 2010).
Os resultados aqui obtidos - associados aos descritores de conhecimento - contribuem, portanto, para um mais amplo entendimento do conteúdo do conhecimento do professor - aqui no âmbito do KoT, relativamente aos tópicos de Medida - e das categorias que o formam, possibilitando um olhar mais detalhado para essa componente da estrutura do conhecimento especializado. Entretanto, para que possamos continuar refletindo sobre essas componentes, algumas questões se abrem, contribuindo para guiar uma agenda de pesquisa que busque, de forma imbricada, uma relação com a formação de professores: (i) que relações ocorrem entre os descritores do conhecimento dos tópicos (KoT) de Medida e outros tópicos, como em Números e Operações?; ii) qual o papel dessas relações na composição estrutural do conhecimento do professor relativamente a esses tópicos?; iii) quais os impactos na prática letiva do professor no caso de as formações (iniciais e contínuas) objetivarem o desenvolvimento do conhecimento do professor associado a essas estruturas matemáticas?; v) de que forma as especificidades do conhecimento do professor se vão desenvolvendo ao longo do tempo, pela participação em contextos formativos que têm essa intencionalidade?











 nueva página del texto (beta)
nueva página del texto (beta)